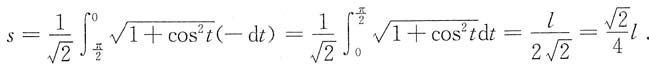一、选择题1. 设f(x)为单调可微函数,g(x)与f(x)互为反函数,且f(2)=4,f'(2)=
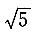
,f'(4)=6,则g'(4)等于______.
A.
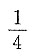
B.
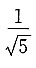
C.
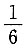
D.4
A B C D
B
[解析] 解:因为
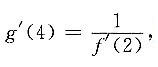
所以选B.
2. 设函数z=f(x,y)在点(x
0,y
0)处有f'
x(x
0,y
0)=a,f'
y(x
0,y
0)=b,则______
A.极限
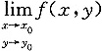
一定存在,但f(x,y)在点(x
0,y
0)处不连续.
B.f(x,y)在点(x
0,y
0)处必连续.
C.dz|
(x0,y0)=adx+bdy.
D.
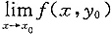
及
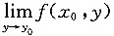
存在且相等.
A B C D
D
[解析] 由f'
x(x
0,y
0)存在知一元函数f(x
0,y
0)在x=x
0处连续,故
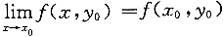
.类似地,由f'
y(x
0,y
0)存在知一元函数f(x
0,y
0)在y=y
0处连续,故
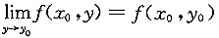
,故选项D正确.
或举反例用排除法.取
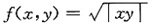
,计算可得f'
x(0,0)=f'
y(0,0)=0,同时可证明

存在,f(x,y)在点(0,0)连续,f(x,y)在点(0,0)处不可微分,这样可排除选项A、C.
取
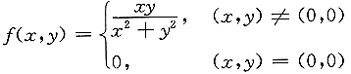
,计算可得f
x'(0,0)=f
y'(0,0)=0,同时可证明f(x,y)在点(0,0)处不连续,这样可排除选项B.由排除法可知,应选D.
3. 设ξ
1,ξ
2,ξ
3,ξ
1+aξ
2-2ξ
3均是非齐次线性方程组Ax=b的解,则对应齐次线性方程组Ax=0有解______
- A.η1=2ξ1+aξ2+ξ3.
- B.η2=-2ξ1+3ξ2-2aξ3.
- C.η3=aξ1+2ξ2-ξ3.
- D.η4=3ξ1-2aξ2+ξ3.
A B C D
D
[解析] 由题设条件Aξi=b,i=1,2,3及A(ξ1+aξ2-2ξ3)=b+ab=b,得(1+a-2)b=b,b≠0,即1+a-2=1,故a=2.
当a=2时,看是否满足Aηi=0,i=1,2,3,4.
Aη1=A(2ξ1+2ξ2+ξ3)=5b≠0,
Aη2=A(-2ξ1+3ξ2-4ξ3)=-3b≠0,
Aη3=A(2ξ1+2ξ2-ξ3)=3b≠0,
Aη4=A(3ξ1-4ξ2+ξ3)=0.
故η4是对应齐次线性方程组Ax=0的解,故应选D.
5. 设向量组(Ⅰ)α
1,α
2,…,α
s,其秩为r
1,向量组(Ⅱ)β
1,β
2,…,β
s,其秩为r
2,且β
i(i=1,2,…,s)均可以由α
1,…,α
s线性表示,则______.
- A.向量组α1+β1,α2+β2,…,αs+βs的秩为r1+r2
- B.向量组α1-β1,α2-β2,…,αs-βs的秩为r1-r2
- C.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1+r2
- D.向量组α1,α2,…,αs,β1,β2,…,βs的秩为r1
A B C D
D
[考点] 向量组的秩
[解析] 设
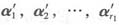
为α
1,α
2,…,α
s的极大无关组,则它也是α
1,α
2,…,α
s,β
1,β
2,…,β
s的极大线性无关组,所以(D)结论成立.
7. 设f(x)在x=0的邻域内连续可导,g(x)在x=0的邻域内连续,且
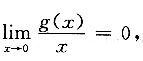
又
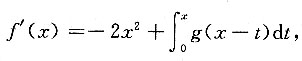
则______.
- A.x=0是f(x)的极大值点
- B.x=0是f(x)的极小值点
- C.(0,f(0))是曲线y=f(x)的拐点
- D.x=0不是f(x)的极值点,(0,f(0))也不是曲线y=f(x)的拐点
A B C D
C
[解析] 由
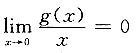
得g(0)=g'(0)=0,f'(0)=0,

因为

所以存在δ>0,当0<|x|<δ时,
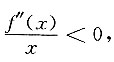
从而当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,选C.
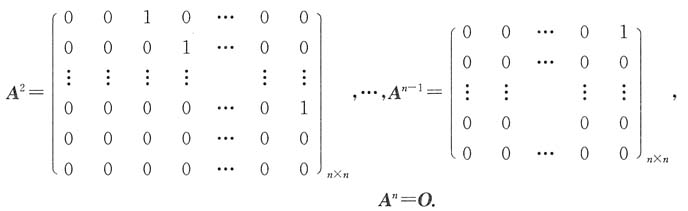
二、填空题1. 设矩阵

则A
3的秩为______.
1.
[解析] 因为
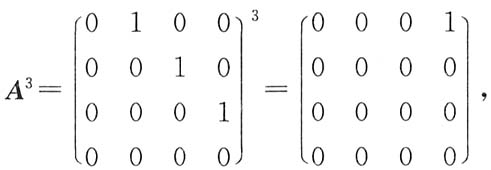
故A
3的秩为1.
计算A
3,可以直接由乘法得到,这是最基本的方法,应熟练掌握.此外,也可由这种矩阵方幂的规律得到:设
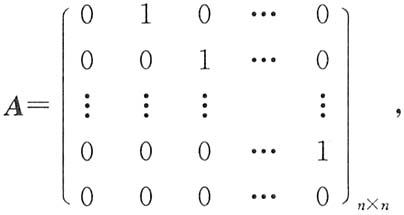
则
2. 设

是f(x)的一个原函数,则

3. 设
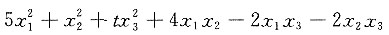
为正定二次型,则t的取值范围是______.
t>2
[解析] 二次型的矩阵为
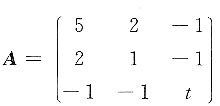
,因为二次型为正定二次型,所以有5>0,
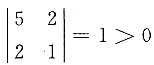
,|A|>0,解得t>2.
4. 设z=f(x+y,y+z,z+x),其中厂连续可偏导,则

[解析] z=f(x+y,y+z,z+x)两边求x求偏导得

解得
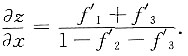
5. 设
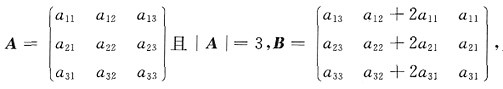
则B*A=______.
[解析] 因为B=AE
12(2)E
13,所以|B|=|A||E
12(2)||E
13|=-3,
又因为B*=|B|B
-1,所以
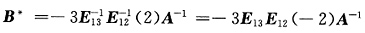
,
故

6. 设
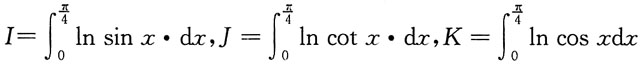
,则I,J,K的大小关系为______.
I<K<J
[考点] 定积分的性质.
比较被积函数在积分区间内的大小次序,利用定积分的性质即可得.
解:当0<x<
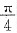
时,有cotx>1>cosx>sinx>0.
从而由y=lnx的单调增加性质,得lncott>lncosx>lnsinx,
根据定积分性质,可得
即I<K<J.
故应填I<K<J.
三、解答题1. 证明:A~B,其中
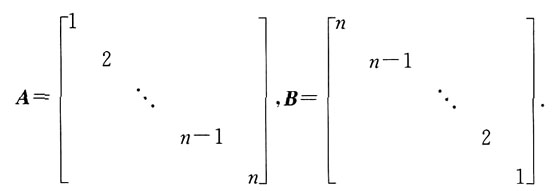
并求可逆矩阵P,使得P
-1AP=B.
证明:由A知,A的全部特征值是1,2,…,n,互不相同,故A相似于由其特征值组成的对角矩阵B.
由于λ
1=1时,(λ
1E-A)X=0,有特征向量ξ
1=[1,0,…,0]
T;
λ
2=2时,(λ
2E-A)X=0,有特征向量ξ
2=[0,1,…,0]
T;
……
λ
n=n时,(λ
nE-A)X=0,有特征向量ξ
n=[0,0,…,1]
T.
故得可逆矩阵
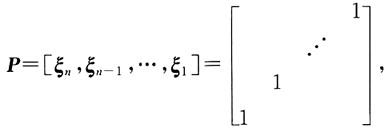
有P
-1AP=B.
2. (Ⅰ)证明:方程x=1+2lnx在(e,+∞)内有唯一实根ε;
(Ⅱ)取x
0满足e<x
0<ε,令x
n=1+2lnx
n-1(n=1,2,…),证明:
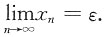
证明:(Ⅰ)令f(x)=x-1-2lnx,则f(e)=e-3<0.又由于
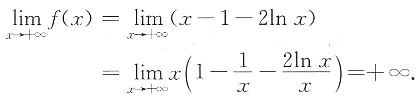
由零点定理,f(x)=0在(e,+∞)内至少有一个实根.
由于
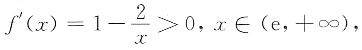
故f(x)=0在(e,+∞)内有唯一实根,记为ε.
(Ⅱ)由(Ⅰ)知,当x∈(e,ε)时,f(x)<0,即
1+2lnx>x.
故当e<x
0<ε时,
x
1=1+2lnx
0>x
0,
x
1=1+2lnx
0<1+2lnε=ε.
假设x
n>x
n-1且x
n<ε,则
x
n+1=1+2lnx
n>x
n,
x
n+1=1+2lnx
n<1+2lnε=ε.
由数学归纳法知,{x
n}单调增加且有上界ε,所以
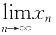
存在,记
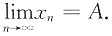
在x
n+1=1+2lnx
n两边同时取极限,得
A=1+2lnA,
即A为方程x=1+2lnx的根.由(Ⅰ)知A=ε,故
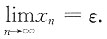
3. 证明:
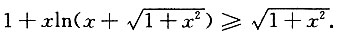
证明:令
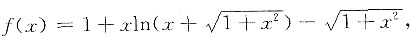
f(0)=0.
方法一
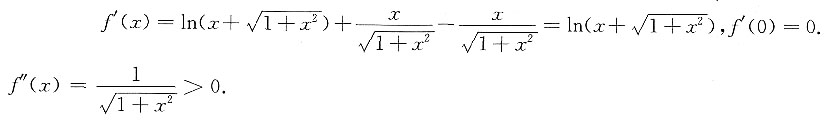
由
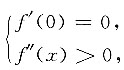
得
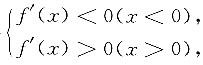
则x=0为f(x)的最小值点,而最小值为f(0)=0,故f(x)≥0,即
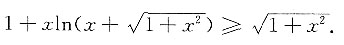
方法二 令
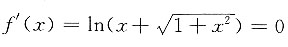
,得x=0,因为
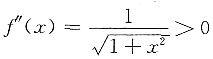
,所以x=0为f(x)的最小值点,最小值为f(0)=0,所以有
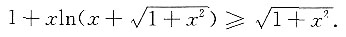
4. 设f(x)在[0,1]上连续,在(0,1)内可导,若在(0,1)内有x
1<x
2,使
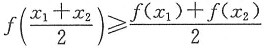
证明:在(0,1)内存在ξ
1,ξ
2,使f'(ξ
1)≥f'(ξ
2).
要产生两个中值点ξ
1与ξ
2满足f'(ξ
1)≥f'(ξ
2),一般要使用两次中值定理.如果令x
0=(x
1+x
2)/2,则有
2f(x
0)≥f(x
1)+f(x
2),
即
f(x
0)-f(x
1)≥f(x
2)-f(x
0).
不等式两边的差值就是使用拉格朗日中值定理的信号.这样问题就解决了.
证明:令
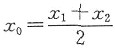
,有

,移项有
f(x
0)-f(x
1)≥f(x
2)-f(x
0). ①
利用拉格朗日中值定理,有
f(x
0)-f(x
1)=f'(ξ
1)(x
0-x
1) ②
f(x
2)-f(x
0)=f'(ξ
2)(x
2-x
0) ③
将式②、式③代入式①,有
f'(ξ
1)(x
0-x
1)≥f'(ξ
2)(x
2-x
0),
因x
0-x
1=x
2-x
0,故有
f'(ξ
1)≥f'(ξ
2).
5. 设平面图形D由摆线
x=a(t-sint),y=a(1-cost),0≤t≤2π,a>0
的第一拱与x轴围成,求该图形D对y轴的面积矩M
y.
解:题中所给的D是一个以摆线一拱
x=a(t-sint),y=a(1-cost),0≤t≤2π,a>0
为上边界,x轴为下边界,从x=0到x=2πa的曲边梯形取竖条,其面积微元为ydx,它对y轴的面积矩为xydx,所以D对y轴的面积矩为

现在按此公式求M
y.
将摆线表达式代入式(*),可以看成将积分变量由x换成t,得

其中

现用一个巧妙的办法计算I
1.令t=2π-u,则

故


所以M
y=3a
3π
2.
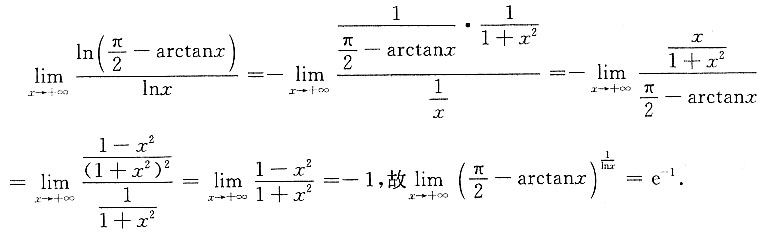
6. 设f(x)在x=a处二阶可导,证明:
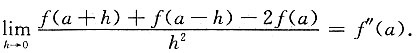
证明:
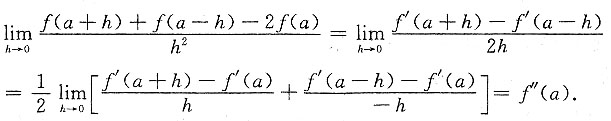
8. 变换二次积分的积分次序:

解:如图所示,积分区域

故

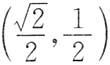 ,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.
,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.9. 求曲线y=f(x)的方程:
解:曲线y=f(x)在点P(x,y)处的法线方程为
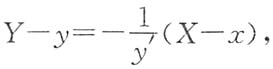
其中(X,Y)为法线上任意一点的坐标.令X=0,则
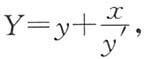
故Q点坐标为
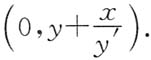
由题设知
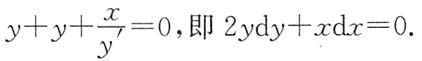
积分得
x
2+2y
2=C.
由
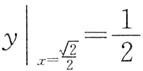
知C=1,故曲线y=f(x)的方程为
x
2+2y
2=1.
10. 已知曲线y=sinx在[0,π]上的弧长为l,试用l表示曲线y=f(x)的弧长s.
解:曲线y=sinx在[0,π]上的弧长为
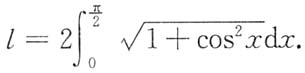
曲线y=f(x)的参数方程为
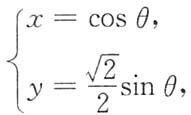
故
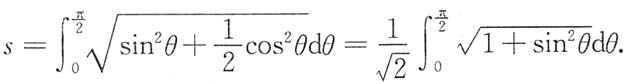
令
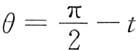
,则
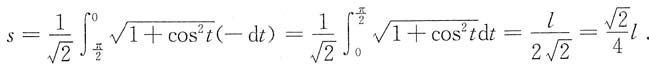
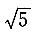 ,f'(4)=6,则g'(4)等于______.
,f'(4)=6,则g'(4)等于______.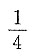
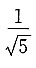
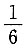
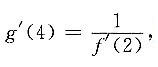 所以选B.
所以选B.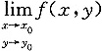 一定存在,但f(x,y)在点(x0,y0)处不连续.
一定存在,但f(x,y)在点(x0,y0)处不连续.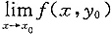 及
及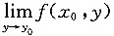 存在且相等.
存在且相等.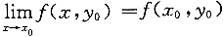 .类似地,由f'y(x0,y0)存在知一元函数f(x0,y0)在y=y0处连续,故
.类似地,由f'y(x0,y0)存在知一元函数f(x0,y0)在y=y0处连续,故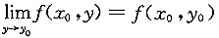 ,故选项D正确.
,故选项D正确.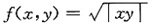 ,计算可得f'x(0,0)=f'y(0,0)=0,同时可证明
,计算可得f'x(0,0)=f'y(0,0)=0,同时可证明 存在,f(x,y)在点(0,0)连续,f(x,y)在点(0,0)处不可微分,这样可排除选项A、C.
存在,f(x,y)在点(0,0)连续,f(x,y)在点(0,0)处不可微分,这样可排除选项A、C.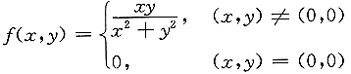 ,计算可得fx'(0,0)=fy'(0,0)=0,同时可证明f(x,y)在点(0,0)处不连续,这样可排除选项B.由排除法可知,应选D.
,计算可得fx'(0,0)=fy'(0,0)=0,同时可证明f(x,y)在点(0,0)处不连续,这样可排除选项B.由排除法可知,应选D.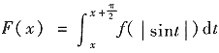 ,则______
,则______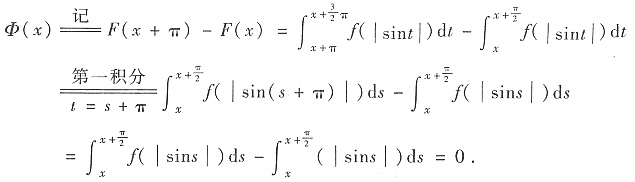
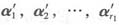 为α1,α2,…,αs的极大无关组,则它也是α1,α2,…,αs,β1,β2,…,βs的极大线性无关组,所以(D)结论成立.
为α1,α2,…,αs的极大无关组,则它也是α1,α2,…,αs,β1,β2,…,βs的极大线性无关组,所以(D)结论成立.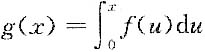 其中
其中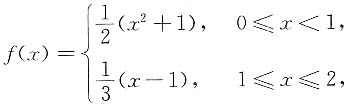 则g(x)在区间(0,2)内______
则g(x)在区间(0,2)内______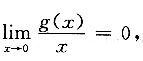 又
又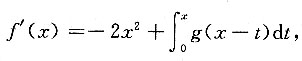 则______.
则______.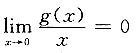 得g(0)=g'(0)=0,f'(0)=0,
得g(0)=g'(0)=0,f'(0)=0,
 所以存在δ>0,当0<|x|<δ时,
所以存在δ>0,当0<|x|<δ时,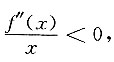 从而当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,选C.
从而当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,选C.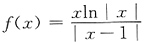 ,则f(x)有______.
,则f(x)有______.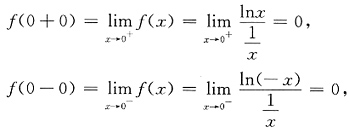
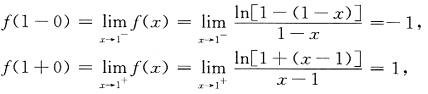
 则A3的秩为______.
则A3的秩为______.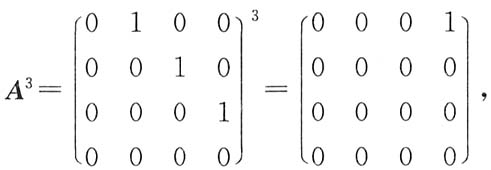
 则
则
 是f(x)的一个原函数,则
是f(x)的一个原函数,则


 是f(x)的原函数,所以
是f(x)的原函数,所以 所以
所以
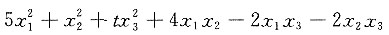 为正定二次型,则t的取值范围是______.
为正定二次型,则t的取值范围是______.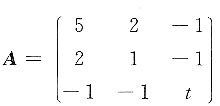 ,因为二次型为正定二次型,所以有5>0,
,因为二次型为正定二次型,所以有5>0,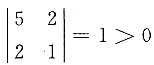 ,|A|>0,解得t>2.
,|A|>0,解得t>2.
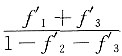
 解得
解得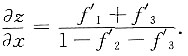
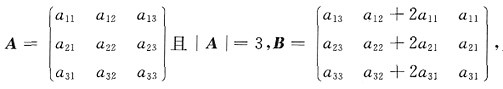 则B*A=______.
则B*A=______.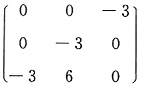
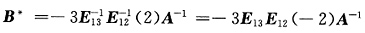 ,
,
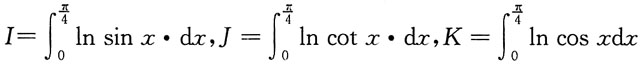 ,则I,J,K的大小关系为______.
,则I,J,K的大小关系为______. 时,有cotx>1>cosx>sinx>0.
时,有cotx>1>cosx>sinx>0.
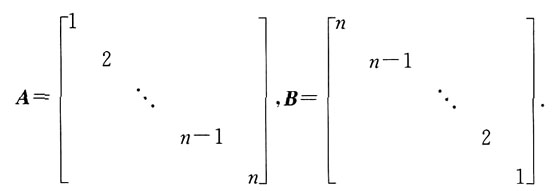
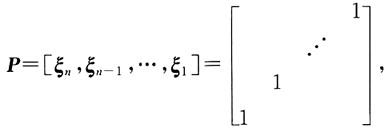
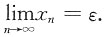
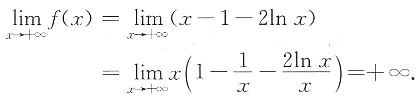
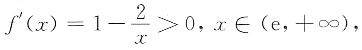
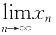 存在,记
存在,记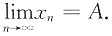
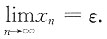
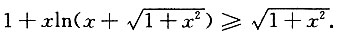
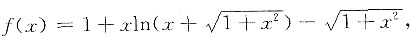 f(0)=0.
f(0)=0.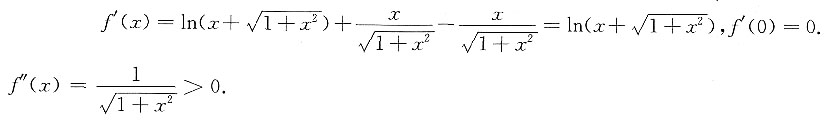
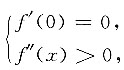 得
得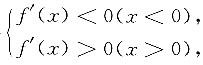 则x=0为f(x)的最小值点,而最小值为f(0)=0,故f(x)≥0,即
则x=0为f(x)的最小值点,而最小值为f(0)=0,故f(x)≥0,即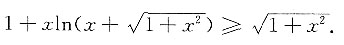
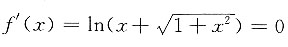 ,得x=0,因为
,得x=0,因为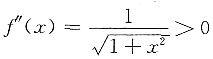 ,所以x=0为f(x)的最小值点,最小值为f(0)=0,所以有
,所以x=0为f(x)的最小值点,最小值为f(0)=0,所以有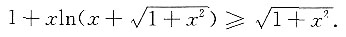
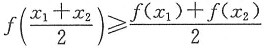
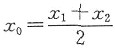 ,有
,有 ,移项有
,移项有





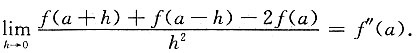
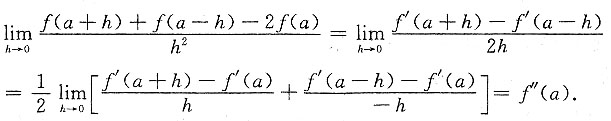
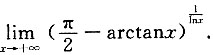
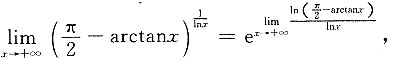

 故
故

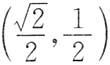 ,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.
,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.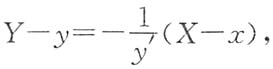
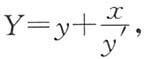
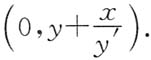 由题设知
由题设知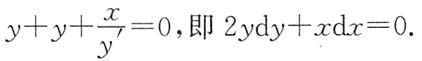
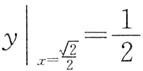 知C=1,故曲线y=f(x)的方程为
知C=1,故曲线y=f(x)的方程为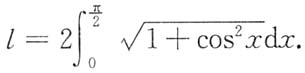
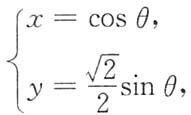
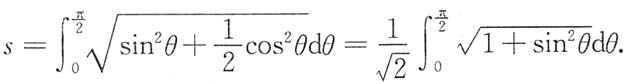
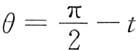 ,则
,则