一、选择题1. 已知P
-1AP=B,若Aα=λα,α≠0,则______
A.B的特征值为λ,对应的特征向量是Pα.
B.B的特征值为
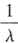
,对应的特征向量是Pα.
C.B的特征值为λ,对应的特征向量是P
-1α.
D.B的特征值为
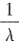
,对应的特征向量是P
-1α.
A B C D
C
[解析] 因为矩阵A与B相似,所以它们有相同的特征值,故可排除B、D.
由P
-1AP=B

P
-1A=BP
-1
P
-1Aα=BP
-1α,于是有
B(P
-1α)=P
-1(λα)=λ(P
-1α).
故应选C.
2. 下列矩阵中,不能相似对角化的矩阵是______
A.

B.

C.

D.

A B C D
D
[解析] A是实对称矩阵,实对称矩阵必可以相似对角化.
B是下三角矩阵,主对角线元素就是矩阵的特征值,因而矩阵有三个不同的特征值,所以矩阵必可以相似对角化.
C是秩为1的矩阵,Ax=0有二个线性无关解,是A的对应于λ=0特征向量.λ=0至少是A的二重特征值,又

,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ
3-4λ
2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
r(0E-A)=r(A)=1
知齐次方程组(0E-A)x=0的基础解系有3-1=2个线性无关的解向量,即λ=0有两个线性无关的特征向量.从而矩阵必可以相似对角化.由排除法,知应选D.或
D是上三角矩阵,主对角线上的元素1,1,-1就是矩阵的特征值,对于二重特征值λ=1,由秩

知齐次方程组(E-A)x=0只有3-2=1个线性无关的解,亦即λ=1只有一个线性无关的特征向量,故矩阵必不能相似对角化.所以应当选D.
3. 设

均是关于x的已知连续函数,y
1(x),y
2(x),y
3(x)是y"+p(x)y'+q(x)y=f(x)的3个线性无关的解,C
1,C
2是两个任意常数,则该非齐次方程的通解是______
- A.C1y1+(C2-C1)y2-(1+C2)y3.
- B.(C1-C2)y1+(C2-1)y2+(1-C1)y3.
- C.(C1+C2)y1+(C1-C2)y2+(1-C1)y3.
- D.C1y1+C2y2+(1-C1-C2)y3.
A B C D
D
[解析] 实际上有下述定理.设p(x),q(x)与f(x)均为连续函数,

考虑下述两个方程
y"+p(x)y'+q(x)y=f(x) (*)
及对应的齐次方程
y"+p(x)y'+q(x)y=0. (**)
①设y
1(x),y
2(x),y
3(x)是式(*)的3个解,A,B,C为常数.并设
y=Ay
1(x)+By
2(x)+Cy
3(x). (***)
则式(***)是式(*)的解的充要条件是
A+B+C=1;
式(***)是式(**)的解的充要条件是
A+B+C=0.
②设y
1(x),y
2(x),y
3(x)是式(*)的3个线性无关的解,A,B,C中有两个为任意常数.
则式(***)是式(*)的通解的充要条件是
A+B+C=1;
式(***)是式(**)的通解的充要条件是
A+B+C=0.
本题用到上述②.验算上述y
1,y
2,y
3的系数之和,D的系数之和为C
1+C
2+(1-C
1-C
2)=1.所以D是通解.
5. 若函数

,在x=0处连续,则______
A.

B.

C.ab=0
D.ab=2
A B C D
A
[解析]

,∵f(x)在x=0处连续,∴

,选A.
6. 设A,B为n阶矩阵,且A与B相似,E为n阶单位矩阵,则______
- A.λE-A=λE-B
- B.A与B有相同的特征值和特征向量
- C.A与B都相似于一个对角矩阵
- D.对任意常数t,tE-A与tE-B相似
A B C D
D
[解析] A与B相似,存在可逆矩阵P,使得P
-1AP=B,则
tE-B=tE-P
-1AP=P
-1(tE)P-P
-1AP=P
-1(tE-A)P,即tE-A与tE-B相似,选D.对于A项:λE-A=λE-B

A=B;对于B项:A与B相似,则A与B有相同的特征值,但特征向量不一定相同;对于C项:A与B不一定能够相似对角化.
8. 已知

,则代数余子式A
21+A
22=______
A B C D
B
[解析] 对行列式|A|按第2行展开,有
2A
21+2A
22+A
23+A
24=9. ①
构造行列式

则|A|和|B|第2行元素代数余子式相同.对|B|按第2行展开,义有
A
21+A
22+2A
23+2A
24=|B|=0. ②
联立①,②可得A
21+A
22=6.故选(B).
作为复习,请你求解:设n阶矩阵

试求:(Ⅰ)|A|中所有元素的代数余子式之和,即

(Ⅱ)|A|中第k行元素代数余子式之和,即

[分析] 直接求|A|中代数余子式之和比较麻烦.由于A的伴随矩阵A
*=(A
ij)
n×n=|A|A
-1,因此只要计算出|A|和A
-1,就可以通过A
*=|A|A
-1求代数余子式之和.
(Ⅰ)按照第1列最后一个元素展开,可得

将矩阵A分块求逆矩阵A
-1.

其中

根据分块矩阵求逆公式,有

于是
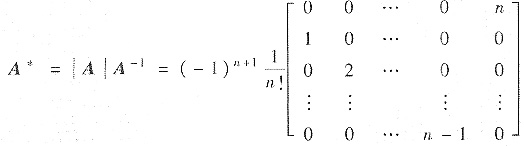
所以

(Ⅱ)根据第(Ⅰ)小题结果,由于

因此

二、填空题1. 设f(u)可导,y=f(x
2)在x
0=-1处取得增量Δx=0.05时,函数增量Δy的线性部分为0.15,则f'(1)=______.
[解析] 由dy=2xf'(x
2)Δx得dy|
x=-1=-2f'(1)×0.05=-0.1f'(1),
因为Δy的线性部分为dy,由-0.1f'(1)=0.15得

.
2. 设正整数n>1,曲线y=x
n2-1在点(1,1)处的切线与x轴的交点为(ε
n,0),则
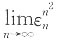
______.
[解析] y'=(n
2-1)x
n2-2,y'(1)=n
2-1,
故切线方程为
y-1=(n
2-1)(x-1).
令y=0,得

故

3. 微分方程

满足初始条件y(1)=1的特解是y=______.
xe1-x
[解析] 此为一阶齐次方程.令y=ux,有

原方程化为

得ln|lnu-1|=ln|C
1x|,
去掉对数记号及绝对值号,得lnu=C
1x+1,u=e
C1x+1,将u|
x=1=1代入,得C
1=-1,u=e
1-x,原方程的解为

4. 已知向量组

与向量组

等秩,则x=______.
1
[解析] 由

知r(α
1,α
2,α
3)=2,由题设:r(β
1,β
2,β
3)=2
因

故x=1.
5. 设

,且α,β,γ两两正交,则a=______,b=______.
-4 -13
[解析] 因为α,β,γ正交,所以

,解得a=-4,b=-13.
6. 设

,而n≥2为正整数,则A
n-2A
n-1=______.
三、解答题1. 设A是3阶矩阵,有特征值λ
1=λ
2=-2,λ
3=2,对应的特征向量分别是

已知β=[3,11,11]
T.证明β是A
100的特征向量,并求对应的特征值.
证明:将β用ξ
1,ξ
2,ξ
3线性表出,设β=x
1ξ
1+x
2ξ
2+x
3ξ
3,即解方程组
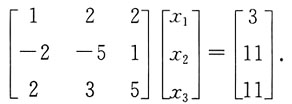
将增广矩阵作初等行变换:

,
解得[x
1,x
2,x
3]
T=[1,-2,3]
T,即β=ξ
1-2ξ
2+3ξ
3,
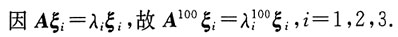
故A
100β=A
100(ξ
1-2ξ
2+3ξ
3)=(-2)
100ξ
1-2(-2)100ξ
2+3×2
100ξ
3 =2
100(ξ
1-2ξ
2+3ξ
3)=2
100β.
得知β是A
100的特征向量,且对应的特征值为2
100.
证明:2. β不是A的特征向量;
证明:已知Aβ=A(ξ1+ξ2+ξ3)=λ1ξ1+λ2ξ2+λ3ξ3.
若β是A的特征向量,假设对应的特征值为μ,则有
Aβ=μβ=μ(ξ1+ξ2+ξ3)=λ1ξ1+λ2ξ2+λ3ξ3,
从而得(μ-λ1)ξ1+(μ-λ2)ξ2+(μ-λ3)ξ3=0.
ξ1,ξ2,ξ3是不同特征值对应的特征向量,由定理知ξ1,ξ2,ξ3线性无关,从而得λ1=λ2=λ3=μ,这和λ1,λ2,λ3互不相同矛盾.故β=ξ1+ξ2+ξ3不是A的特征向量.
3. 向量组β,Aβ,A
2β线性无关.
证明:
法一 用线性无关的定义证.
假设存在数k
1,k
2,k
3,使得 k
1β+k
2Aβ+k
3A
2β=0.
由β=ξ
1+ξ
2+ξ
3及Aξ
i=λ
iξ
i,i=1,2,3,代入得
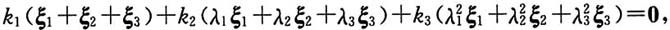
整理得

因ξ
1,ξ
2,ξ
3线性无关,则有

又λ
i(i=1,2,3)互不相同,故方程组(*)的系数矩阵的行列式

故方程组(*)仅有零解,即k
1=k
2=k
3=0,所以β,Aβ,A
2β线性无关.
法二 用等价向量组、初等变换、秩等论证.因

其中

所以C是可逆矩阵.
故r(β,Aβ,A
2β)=r(ξ
1,ξ
2,ξ
3)=3.因此β,Aβ,A
2β线性无关.
4. 求

解:

5. 设A是正交矩阵,且|A|<0.证明:|E+A|=0.
证明:因为A是正交矩阵,所以ATA=E,两边取行列式得|A|2=1,因为|A|<0,所以|A|=-1.
由|E+A|=|ATA+A|=|(AT+E)A|=|A||AT+E|=-|AT+E|
=-|(A+E)|T=-|E+A|
得|E+A|=0.
6. 设x>0,常数a>e.证明:(a+x)
a<a
a+x.
证明:由函数y=lnx的单调性,只需证aln(a+x)<(a+x)lna.
设f(x)=(a+x)lna-aln(a+x),则f(x)在[0,+∞)内连续、可导,且

所以f(x)在[0,+∞)内单增.又f(0)=0.从而得f(x)>0,x>0,即
aln(a+x)<(a+x)lna,x>0.
所以(a+x)
a<a
a+x,x>0.
7. (Ⅰ)求定积分

(Ⅱ)对于(Ⅰ)中的a
n,证明a
n+1<a
n(n=1,2,…)且

(Ⅰ)解:当n≥2时,计算

作积分变量代换,令1-x=t,是

下面用分部积分法计算:

所以

由此迭代式得

其中

(Ⅱ)证明:由(Ⅰ)知a
n的迭代式显然有0<a
n<a
n-1(n=2,3,…).又

则

8. 设f(u)在区间[-1,1]上连续,且

求二重积分

的值.
解:先画出积分区域D={(x,y)||x|+|y|≤1},如图(a)所示.

对于

的内层,对y的积分作积分变量代换,令u=x+y.当y=-1-x时,u=-1;当y=1+x时,u=1+2x.于是

再交换x与u的积分次序(如图(b)),得

类似地,

从而

9. 杆AB与质点C的相互吸引力;
解:如图所示,杆AB的线密度为

,于是位于[x,x+dx]上微元的质量为

,它与质点C的引力在y轴上的分力为

10. 当质点C在杆AB的中垂线上从点C沿y轴移向无穷远处时,克服引力所做的功.
解:根据上面的计算,当质点C位于坐标y处时,引力的大小为

于是

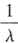 ,对应的特征向量是Pα.
,对应的特征向量是Pα.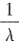 ,对应的特征向量是P-1α.
,对应的特征向量是P-1α. P-1A=BP-1
P-1A=BP-1 P-1Aα=BP-1α,于是有
P-1Aα=BP-1α,于是有



 ,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ3-4λ2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
,故λ=0是二重特征值A相似于对角阵或由|λE-A|=λ3-4λ2,知矩阵的特征值是4,0,0.对于二重根λ=0,由秩
 均是关于x的已知连续函数,y1(x),y2(x),y3(x)是y"+p(x)y'+q(x)y=f(x)的3个线性无关的解,C1,C2是两个任意常数,则该非齐次方程的通解是______
均是关于x的已知连续函数,y1(x),y2(x),y3(x)是y"+p(x)y'+q(x)y=f(x)的3个线性无关的解,C1,C2是两个任意常数,则该非齐次方程的通解是______ 考虑下述两个方程
考虑下述两个方程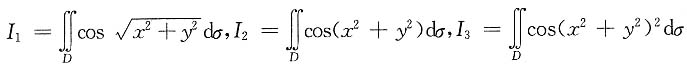 ,其中D={(x,y)|x2+y2≤1},则______
,其中D={(x,y)|x2+y2≤1},则______ ,在x=0处连续,则______
,在x=0处连续,则______

 ,∵f(x)在x=0处连续,∴
,∵f(x)在x=0处连续,∴ ,选A.
,选A. A=B;对于B项:A与B相似,则A与B有相同的特征值,但特征向量不一定相同;对于C项:A与B不一定能够相似对角化.
A=B;对于B项:A与B相似,则A与B有相同的特征值,但特征向量不一定相同;对于C项:A与B不一定能够相似对角化.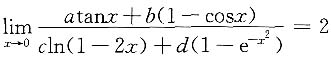 ,其中a2+c2≠0,则必有______.
,其中a2+c2≠0,则必有______. ,则代数余子式A21+A22=______
,则代数余子式A21+A22=______











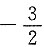
 .
.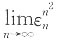 ______.
______.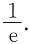


 满足初始条件y(1)=1的特解是y=______.
满足初始条件y(1)=1的特解是y=______. 原方程化为
原方程化为





 ,且α,β,γ两两正交,则a=______,b=______.
,且α,β,γ两两正交,则a=______,b=______. ,解得a=-4,b=-13.
,解得a=-4,b=-13. ,而n≥2为正整数,则An-2An-1=______.
,而n≥2为正整数,则An-2An-1=______.
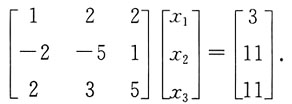
 ,
,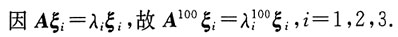
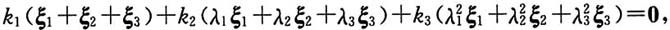




 所以C是可逆矩阵.
所以C是可逆矩阵.




 作积分变量代换,令1-x=t,是
作积分变量代换,令1-x=t,是






 求二重积分
求二重积分 的值.
的值.







 ,于是位于[x,x+dx]上微元的质量为
,于是位于[x,x+dx]上微元的质量为 ,它与质点C的引力在y轴上的分力为
,它与质点C的引力在y轴上的分力为

 于是
于是
