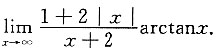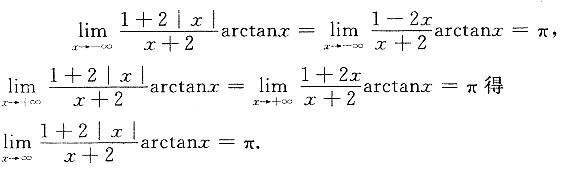一、选择题1. 设
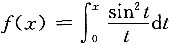
,
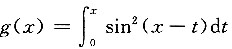
,则当x→0时,g(x)是f(x)的______.
- A.高阶无穷小
- B.低阶无穷小
- C.同阶但非等价的无穷小
- D.等价无穷小
A B C D
A
[解析] 由
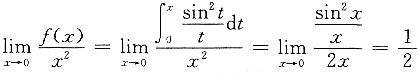
得当x→0时,
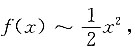
又
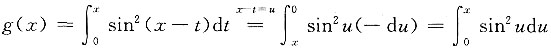
,
由
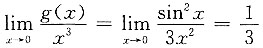
得当x→0时,
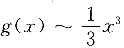
,
故g(x)是f(x)的高阶无穷小,应选A.
2. 累次积分
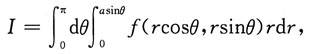
其中a>0为常数,则I可写成______
A.
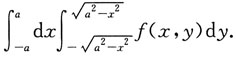
B.
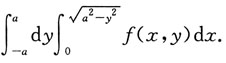
C.
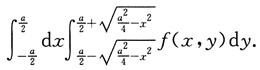
D.
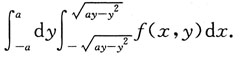
A B C D
C
[解析] 这是把极坐标系下的累次积分转换成Oxy直角坐标系下的累次积分的问题.先将I表成
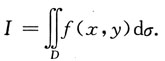
由D的极坐标表示:
0≤θ≤π,0≤r≤asinθ
即r
2=x
2+y
2≤arsinθ=ay
可知
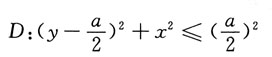
如下图.
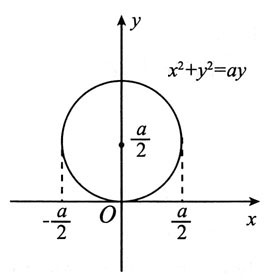
若是先y后x的积分顺序,则
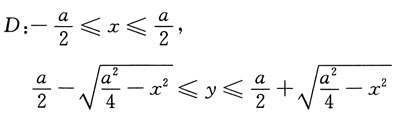
于是
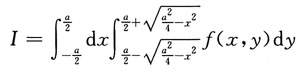
因此选C.
若是先x后y的积分顺序应是
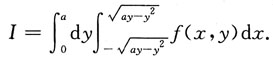
5. 设f(x,y)=|x-y|φ(x,y),其中φ(x,y)在点(0,0)的某邻域内连续,则φ(0,0)=0是f(x,y)在点(0,0)处可微的______
- A.必要条件但非充分条件.
- B.充分条件但非必要条件.
- C.充分必要条件.
- D.既非充分又非必要条件.
A B C D
C
[解析] 先证充分性.设φ(0,0)=0,由于φ(x,y)在点(0,0)处连续,所以
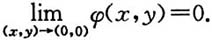
由于
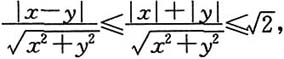
故
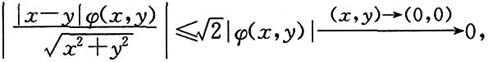
所以
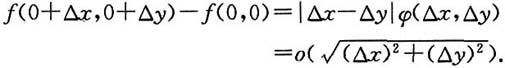
按可微定义,f(x,y)在点O(0,0)处可微,且df(x,y)=0·Δx+0·Δy,即f'
x(0,0)=0,f'
y(0,0)=0.
再证必要性.设f(x,y)在点(0,0)处可微,则f'
x(0,0)与f'
y(0,0)必都存在.
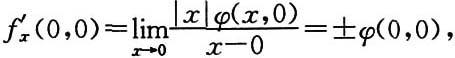
其中x→0
+时,取“+”,x→0
-时,取“-”.
由于f'
x(0,0)存在,所以φ(0,0)=-φ(0,0),从而φ(0,0)=0.证毕.
6. 设A是n阶矩阵,对于齐次线性方程组(Ⅰ)A
nx=0和(Ⅱ)A
n+1x=0,现有四个命题
(1)(Ⅰ)的解必是(Ⅱ)的解. (2)(Ⅱ)的解必是(Ⅰ)的解.
(3)(Ⅰ)的解不是(Ⅱ)的解. (4)(Ⅱ)的解不是(Ⅰ)的解.
以上命题中正确的是______
- A.(1)(2).
- B.(1)(4).
- C.(3)(4).
- D.(2)(3).
A B C D
A
[解析] 若Anα=0,则An+1α=A(Anα)=A0=0,即若α是(Ⅰ)的解,则α必是(Ⅱ)的解,可见命题(1)正确,
如果An+1α=0,而Anα≠0,那么对于向量组α,A1α,A2α,…,Anα,一方面有:
若kα+k1A1α+k2A2α+…+knAnα=0,用An左乘上式的两边,并把An+1α=0,An+2α=0…代入,得kAnα=0.由Anα≠0知,必有k=0.类似地用An-1左乘可得k1=0.因此,α,A1α,A2α,…,Anα线性无关.
但另一方面,这是n+1个n维向量,它们必然线性相关,两者矛盾.故An+1α=0时,必有Anα=0,即(Ⅱ)的解必是(Ⅰ)的解.因此命题(2)正确.
所以应选A.
8. 去看待已知α
1=(1,1,-1)
T,α
2=(1,2,0)
T是齐次方程组Ax=0的基础解系,那么下列向量中Ax=0的解向量是______
- A.(1,-1,3)T.
- B.(2,1,-3)T.
- C.(2,2,-5)T.
- D.(2,-2,6)T.
A B C D
B
[解析] 记选项A,B,C,D中向量分别是ξ
1,ξ
2,ξ
3,ξ
4,因ξ
1,ξ
4成比例,如果A是Ax=0的解,则D必是Ax=0的解.因此A、D均不是Ax=0的解.
由于α
1,α
2是Ax=0的基础解系,那么α
1,α
2可表示Ax=0的任何一个解ξ,亦即方程组x
1α
1+x
2α
2=ξ必有解.因为

可见第2个方程组无解,即ξ
3=(2,2,-5)
T不能由α
1,α
2线性表出.故C不成立,应选B.
二、填空题1.
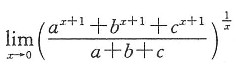
=______.
[解析] 利用幂指函数极限的求法求之.求解时要注意利用等价无穷小代换:
a
x-1~xlna(x→0)
原式=
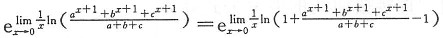
,
而
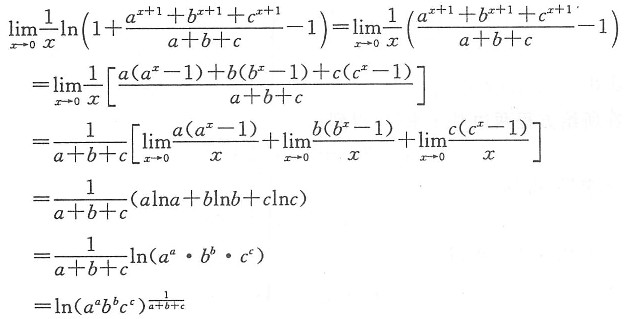
故 原式=
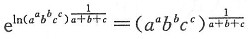
2. 设α
1,α
2,α
3均为三维列向量,记矩阵
A=(α
1,α
2,α
3),B=(α
1+α
2+α
3,α
1+2α
2+4α
3,α
1+3α
2+9α
3).如果|A|=1,那么|B|=______.
2.
[解析] 解法1 利用行列式的性质计算.
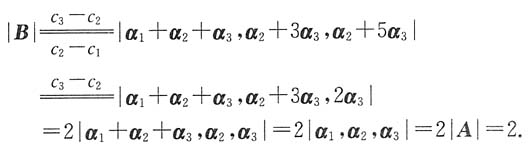
解法2 利用矩阵的性质计算.
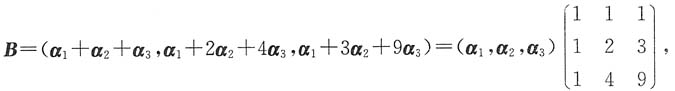
则

3. 设函数z=z(x,y)具有二阶连续的偏导数,满足
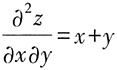
,z(x,0)=0,z(0,y)=y
2,则z(x,y)=______。
[考点] 本题先对x进行积分,得出含y的未知函数的偏导表达式,再对y进行积分,得出含有x的未知函数的表达式,结合z(x,0)=0,z(0,y)=y
2得出结果。
[解析] 因为
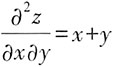
,对x积分可得
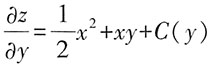
,
令x=0可得
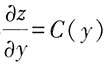
,又因为z(0,y)=y
2,对y求导
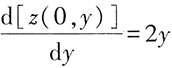
,可以得到C(y)=2y,
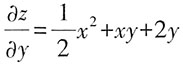
,
再对y积分可得
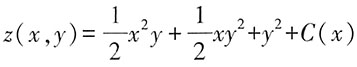
令y=0可以得到z(x,0)=0=C(x),则
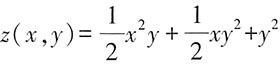
。
4. 圆周x
2+y
2=16与直线

围成的小的那块弓形状的图形绕该直线L旋转一周生成的旋转体(形如橄榄状)的体积V=______.
[解析] 原点到直线

的距离

所以直线y=2与圆周x
2+y
2=16围成的小的那块弓形状的图形绕直线y=2旋转一周生成的旋转体体积与题中要求的旋转体体积相同.由此有

其中


故

5.
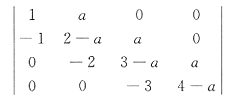
=______.
24
[解析] 在用按行(列)展开公式计算行列式的值时,应先用行列式的性质作恒等变形.以期减少计算量.将a
12=-1,a
23=-2,a
34=-3消为零,行列式变形成上三角行列式,计算得
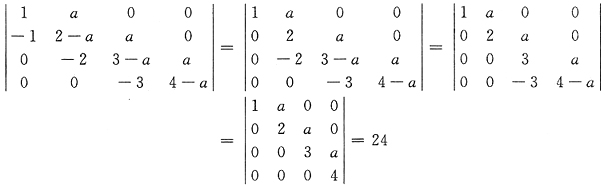
6. 设常数a>0,由方程组
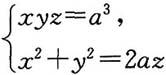
确定的满足y(a)=a,z(a)=a的函数组y=y(x),z=z(x)的y'(a)=______,z'(a)=______.
-1;0
[解析] 方程两边对x求导,得yz+xy'z+xyz'=0及x+yy'=az'.将(x,y,z)=(a,a,a)代入得y'(a)+z'(a)=-1,y'(a)-z'(a)=-1.解得y'(a)=-1,z'(a)=0.
三、解答题设A,B是n阶矩阵,证明:1. 当A可逆时,AB和BA有相同的特征值;
证明:当A可逆时,因A-1(AB)A=(A-1A)BA=BA,故AB~BA.相似矩阵有相同的特征值,故AB和BA有相同的特征值.
2. 证明AB和BA有相同的特征值.
证明:思路一:若AB有特征值λ=0,则|AB|=|A||B|=|BA|=0,故BA也有特征值λ=0;若AB有特征值λ≠0,并设相应的特征向量为α(≠0),即
(AB)α=λα,(α≠0) (*)
式(*)左乘B,得B(AB)α=λBα
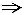
(BA)(Bα)=λBα,其中Bα≠0,(若Bα=0,则由式(*)(AB)α=A(Bα)=0,这和λ≠0且α≠0矛盾),故BA也有特征值λ≠0,对应的特征向量为Bα,得证AB和BA有相同的特征值.
思路二:AB有特征值λ=0,则|AB|=|A||B|=|BA|=0,故BA也有特征值λ=0;
若λ≠0,则

则当λ≠0时,AB和BA有相同的特征值.
注:思路二中利用了分块初等矩阵和分块初等变换的思想,仅供参考.
3. 设函数f(x)在[0,1]上连续,(0,1)内可导,且
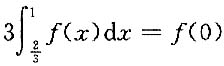
,证明:在(0,1)内存在一个ξ,使f'(ξ)=0.
证明:
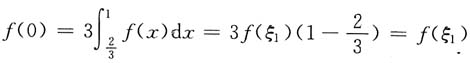
,其中
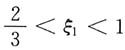
.由罗尔定理,存在ξ,满足0<ξ<ξ
1,且f'(ξ)=0.
4. A是3阶矩阵,有特征值λ
1=λ
2=2,对应两个线性无关的特征向量为ξ
1,ξ
2,λ
3=-2对应的特征向量是ξ
3.
(Ⅰ)问ξ
1+ξ
2是否是A的特征向量?说明理由;
(Ⅱ)问ξ
2+ξ
3是否是A的特征向量?说明理由;
(Ⅲ)证明任意3维非零向量β都是A
2的特征向量,并求对应的特征值.
(Ⅰ)解:ξ1+ξ2仍是A的对应于λ1=λ2=2的特征向量.
因已知Aξ1=2ξ1,Aξ2=2ξ2,故
A(ξ1+ξ2)=Aξ1+Aξ2=2ξ1+2ξ2=2(ξ1+ξ2).
(Ⅱ)解:ξ2+ξ3不是A的特征向量.假设是,设其对应的特征值为μ,则有
A(ξ2+ξ3)=μ(ξ2+ξ3),
得2ξ2-2ξ3-μξ2-μξ3=(2-μ)ξ2-(2+μ)ξ3=0,
因2-μ和2+μ不同时为零,故ξ2,ξ3线性相关,这和不同特征值对应的特征向量线性无关矛盾,
故ξ2+ξ3不是A的特征向量.
(Ⅲ)[证] 因A有特征值λ1=λ2=2,λ3=-2,故A2有特征值μ1=μ2=μ3=4.对应的特征向量仍是ξ1,ξ2,ξ3,且ξ1,ξ2,ξ3线性无关故存在可逆矩阵P=(ξ1,ξ2,ξ3),使得
P-1A2P=4E,A2=P(4E)P-1=4E,
从而对任意的β≠0,有A2β=4Eβ=4β,故知任意3维非零向量β都是A2的对应于特征值μ=4的特征向量.
5. 若n阶矩阵A满足AA
T=E,其中E是n阶单位矩阵,则称A为正交矩阵.证明:
(Ⅰ)若A,B是n阶正交矩阵,则A
TB也是n阶正交矩阵;
(Ⅱ)若λ是正交矩阵A的实特征值,则λ只可能是1或-1;
(Ⅲ)若|A||B|<0,则|A+B|=|A|+|B|.
证明:A,B为正交矩阵,则AA
T=E,|A|=|A
T|

|A|
2=1

|A|=±1;同理有|B|=±1.因此|A|+|B|=0或±2.
(Ⅰ)A为正交矩阵,则有AA
T=E,即A
-1=A
T,从而有
A
-1(A
-1)
T=A
T(A
-1)
T=(A
-1A)
T=E,
由此证得A
-1,A
T为正交矩阵.
A,B为正交矩阵,则
(AB)(AB)
T=ABB
TA
T=A(BB
T)A
T=AA
T=E,
所以AB也为正交矩阵.
综上可知A
TB也为正交矩阵.
(Ⅱ)若A为正交矩阵,λ是A的实特征值,设p≠0为相应λ的特征向量,则
Ap=λp

p
TA
T=λp
T 
p
TA
T(Ap)=λp
T(λp)

p
T(A
TA)p=λ
2(p
Tp)

p
Tp=λ
2(p
Tp).
由p
Tp≠0

λ
2=1.由于λ是实数,因此λ只可能是1或-1.
(Ⅲ)|A+B|=|A||E+A
-1B|=±|E+A
-1B|=±|E+A
TB|.
因为A
TB是正交矩阵,又|A
TB|=|A
T|·|B|=|A|·|B|=|AB|<0.
因为A
TB所有特征值之积等于A
TB的行列式,即-1;而且复特征值必共轭出现,其积必为正数;而实特征值不是+1就是-1,从而可知正交矩阵A
TB的特征值中必有λ=-1.从而有|A
TB-λE|=0,即|A+B|=0.
由于|A|=|B|=±1,所以|A|+|B|=0或±2.
综上,当|A||B|<0时,|A+B|=|A|+|B|=0.
6. 求极限
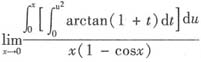
.
解:
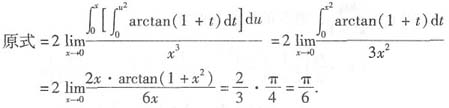
[考点] 变上限定积分求导、洛必达法则、等价无穷小
7. 设

试问当α取何值时,f(x)在点x=0处(1)连续;(2)可导;(3)一阶导数连续;(4)二阶导数存在.
解:(1)因当α≤0时,极限

不存在;当α>0时,

所以
当α>0时,f(x)在x=0处连续.
(2)

当α-1>0时,即α>1时,f'(0)=0,f(x)在x=0处可导.
(3)


当α>2时,

f(x)在x=0处一阶导数连续.
(4)

当α≤3时,f"(0)不存在;当α>3时,f"(0)=0,即f(x)在点x=0处二阶可导.
8. 已知函数y=y(x)满足微分方程x
2+y
2y'=1-y',且y(2)=0,求y(x)的极大值与极小值.
解:由x
2+y
2y'=1-y',得
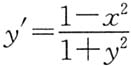
.令y'=0,得x=±1.
当x<-1时,y'<0;当-1<x<1时,y'>0;当x>1时,y'<0.因此,x=-1为其极小值点,x=1为其极大值点.
将原方程分离变量后得 (1+y
2)dy=(1-x
2)dx,
其通解为 x
3+y
3-3x+3y=C.
又y(2)=0,得C=2.故x
3+y
3-3x+3y=2.
所以,y(x)的极小值为y(-1)0,y(x)的极大值为y(1)=1.
9. 求
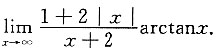
解:由
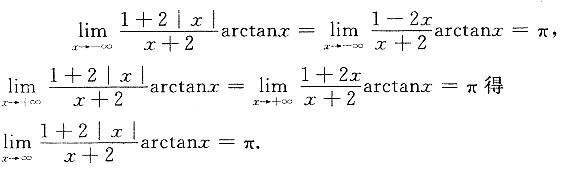
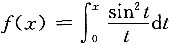 ,
,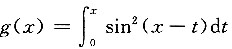 ,则当x→0时,g(x)是f(x)的______.
,则当x→0时,g(x)是f(x)的______.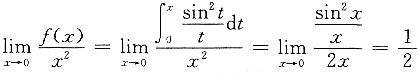 得当x→0时,
得当x→0时,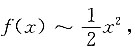
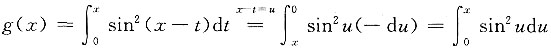 ,
,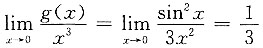 得当x→0时,
得当x→0时,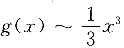 ,
,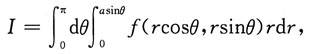 其中a>0为常数,则I可写成______
其中a>0为常数,则I可写成______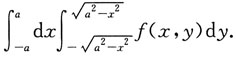
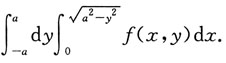

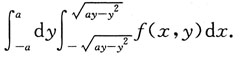
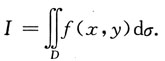 由D的极坐标表示:
由D的极坐标表示: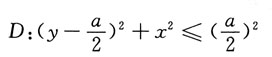

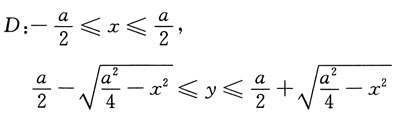


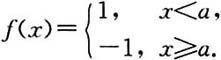
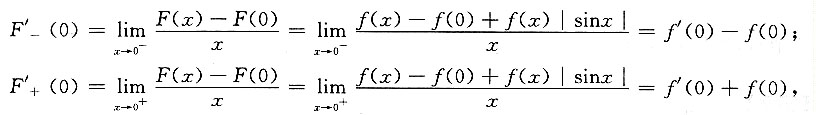
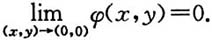 由于
由于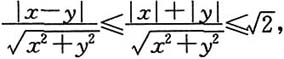
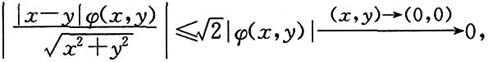
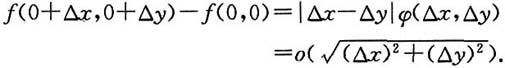
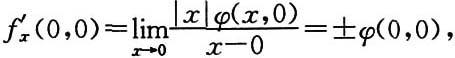

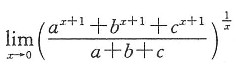 =______.
=______.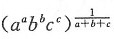
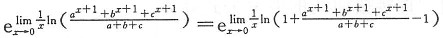 ,
,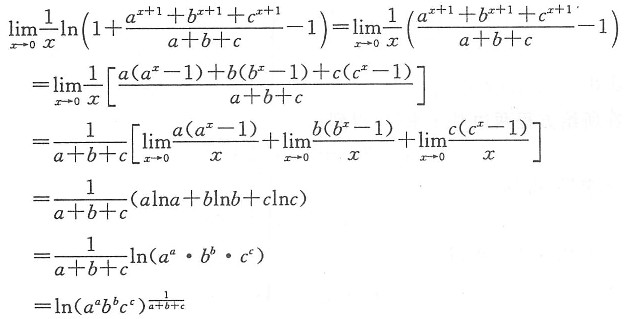
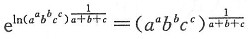
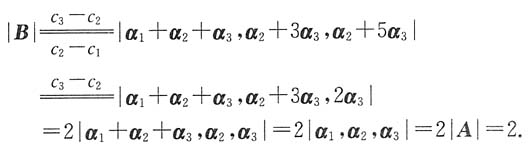
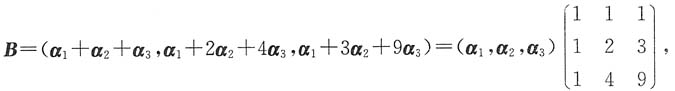

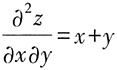 ,z(x,0)=0,z(0,y)=y2,则z(x,y)=______。
,z(x,0)=0,z(0,y)=y2,则z(x,y)=______。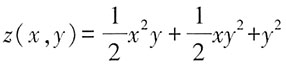
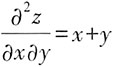 ,对x积分可得
,对x积分可得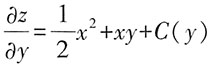 ,
,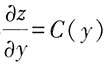 ,又因为z(0,y)=y2,对y求导
,又因为z(0,y)=y2,对y求导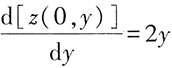 ,可以得到C(y)=2y,
,可以得到C(y)=2y,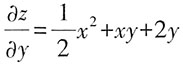 ,
,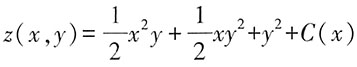
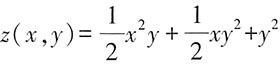 。
。 围成的小的那块弓形状的图形绕该直线L旋转一周生成的旋转体(形如橄榄状)的体积V=______.
围成的小的那块弓形状的图形绕该直线L旋转一周生成的旋转体(形如橄榄状)的体积V=______.
 的距离
的距离




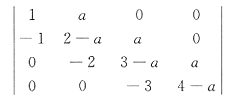 =______.
=______.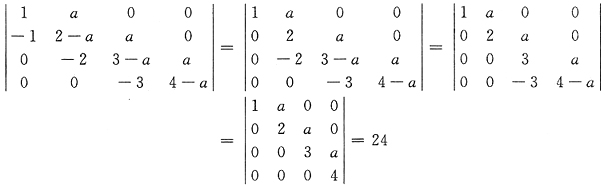
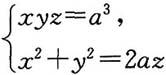 确定的满足y(a)=a,z(a)=a的函数组y=y(x),z=z(x)的y'(a)=______,z'(a)=______.
确定的满足y(a)=a,z(a)=a的函数组y=y(x),z=z(x)的y'(a)=______,z'(a)=______.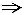 (BA)(Bα)=λBα,其中Bα≠0,(若Bα=0,则由式(*)(AB)α=A(Bα)=0,这和λ≠0且α≠0矛盾),故BA也有特征值λ≠0,对应的特征向量为Bα,得证AB和BA有相同的特征值.
(BA)(Bα)=λBα,其中Bα≠0,(若Bα=0,则由式(*)(AB)α=A(Bα)=0,这和λ≠0且α≠0矛盾),故BA也有特征值λ≠0,对应的特征向量为Bα,得证AB和BA有相同的特征值.
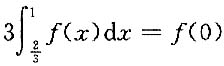 ,证明:在(0,1)内存在一个ξ,使f'(ξ)=0.
,证明:在(0,1)内存在一个ξ,使f'(ξ)=0.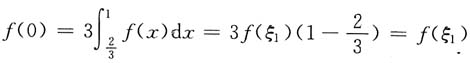 ,其中
,其中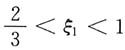 .由罗尔定理,存在ξ,满足0<ξ<ξ1,且f'(ξ)=0.
.由罗尔定理,存在ξ,满足0<ξ<ξ1,且f'(ξ)=0. |A|2=1
|A|2=1 |A|=±1;同理有|B|=±1.因此|A|+|B|=0或±2.
|A|=±1;同理有|B|=±1.因此|A|+|B|=0或±2. pTAT=λpT
pTAT=λpT pTAT(Ap)=λpT(λp)
pTAT(Ap)=λpT(λp) pT(ATA)p=λ2(pTp)
pT(ATA)p=λ2(pTp) pTp=λ2(pTp).
pTp=λ2(pTp). λ2=1.由于λ是实数,因此λ只可能是1或-1.
λ2=1.由于λ是实数,因此λ只可能是1或-1.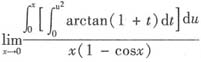 .
.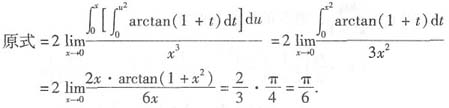
 试问当α取何值时,f(x)在点x=0处(1)连续;(2)可导;(3)一阶导数连续;(4)二阶导数存在.
试问当α取何值时,f(x)在点x=0处(1)连续;(2)可导;(3)一阶导数连续;(4)二阶导数存在. 不存在;当α>0时,
不存在;当α>0时, 所以
所以


 f(x)在x=0处一阶导数连续.
f(x)在x=0处一阶导数连续.
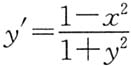 .令y'=0,得x=±1.
.令y'=0,得x=±1.