第一部分 客观题9. 从一瓶浓度为20%的消毒液中倒出
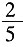
后,加满清水,再倒出
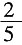
,又加满清水,此时消毒液的浓度为______。
A B C D
A
[解析] 每一次稀释,溶质的量都变为原来的
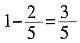
,而溶液的量不变,则浓度也变为原来的
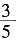
,因此最后的浓度为20%×
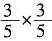
=7.2%。
18. 下列计算正确的是______。
A.(-8)-8=0
B.
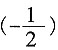
×(-2)=1
C.-(-1)
0=1
D.|-2|=-2
A B C D
B
[解析] A项,(-8)-8=-16,此选项错误;B项,
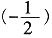
×(-2)=1,此选项正确;C项,-(-1)
0=-1,此选项错误;D项,|-2|=2,此选项错误。故选B。
22. 在“x
2□2xy□y
2”的空格口中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是______。
A.
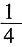
B.

C.
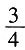
D.1
A B C D
B
[解析] 综上共有如下四种情况:
| 编号
|
第一个空格所填
|
第二个空格所填
|
| ①
|
+
|
+
|
| ②
|
+
|
-
|
| ③
|
-
|
-
|
| ④
|
-
|
+
|
若要成为完全平方式,则需为第①或者第④种,故概率为
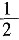
。
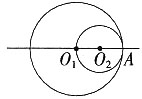
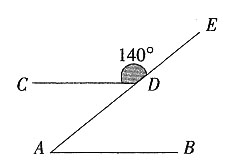
23. 如图,⊙O
1和⊙O
2内切于点A,其半径分别为4和2,将⊙O
2沿直线O
1O
2平移至两圆外切时,⊙O
2移动的距离是______。
A B C D
D
[解析] ⊙O2可以向左或者向右移动,图中O1O2的距离为4-2=2,若向右移动,当相切时O1O2距离变为4+2=6,故⊙O2移动的距离是6-2=4,若向左移动,⊙O2移动的距离是6+2=8。故选择D。
25. 已知点(-5,y
1),(1,y
2),(10,y
3)在函数y=(x-2)
2+c的图象上,则y
1,y
2,y
3的大小关系是______。
- A.y1>y2>y3
- B.y3>y1>y2
- C.y3>y2>y1
- D.y2>y1>y3
A B C D
B
[解析] 将x1=-5,x2=1,x3=10代入函数得:y1=49+c,y2=1+c,y3=64+c,故选择B。
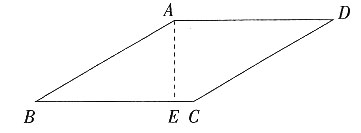
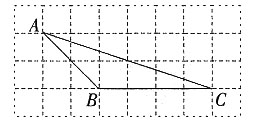
28. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°。在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为______。
A.6
B.3
C.
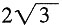
D.
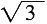
A B C D
C
[解析] ∵∠ACB=90°,BC=3,AB=6,∴sinA=BC:AB=1:2,∴∠A=30°,∠CBA=60°。根据折叠的性质知,∠CBE=∠EBA=
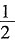
∠CBA=30°,∴CE=BCtan30°=
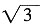
,∴DE=2CE=
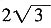
。故选C。
31. 下列计算正确的是______。
A.
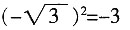
B.
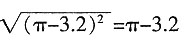
C.
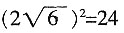
D.
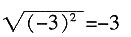
A B C D
C
[解析]
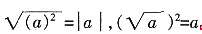
。
37. 暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为______。
A.
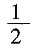
B.
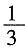
C.
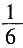
D.
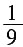
A B C D
B
[解析] 画树状图得:∵共有9种等可能的结果,小明和小亮选到同一社区参加实践活动的有3种情况,∴小明和小亮选到同一社区参加实践活动的概率为:
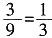
。故选B。
38. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为______。
A.
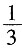
C.
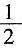
B.
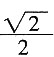
D.3
A B C D
A
[解析] 由图形知:tan∠ACB=
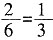
,故选A。
43. 已知m,n是方程x
2+
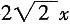
+1=0的两根,则代数式
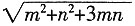
的值为______。
A B C D
C
[解析] m,n是方程x
2+
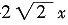
+1=0的两根,∴m+n=
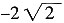
,mn=1,
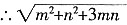
=
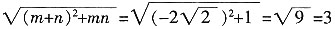
,故选C。
44. 以下说法正确的有______。
①正八边形的每个内角都是135°
②
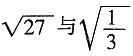
是同类二次根式
③长度等于半径的弦所对的圆周角为30°
④反比例函数
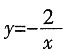
,当x<0时,y随x的增大而增大
A B C D
C
[解析] ①正八边形的每个内角都是
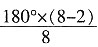
=135°,故①正确;②
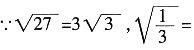
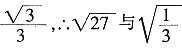
是同类二次根式;故②正确;③如图:∵OA=OB=AB,∴AOB=60°,∴∠C=
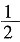
∠AOB=30°,∴∠D=180°-∠C=150°,∴长度等于半径的弦所对的圆周角为30°或150°;故③错误;④反比例函数y=
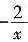
,当x<0时,y随x的增大而增大。故④正确。故正确的有①②④,共3个,故选C。
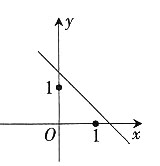
46. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=1,BD=2,则
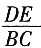
的值为______。
A.
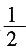
B.
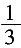
C.
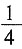
D.
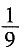
A B C D
B
[解析]
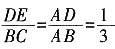
。
一、简答题(满分12分)1. 甲、乙两人绕城而行,甲每小时行8千米,乙每小时行6千米。现在两人同时从同一地点相背出发,乙遇到甲后,再行4小时回到原出发点。求乙绕城一周所需要的时间?
甲乙速度比=8:6:4:3,相遇时乙行了全程的
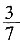
,那么4小时就是行全程的
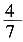
,所以乙行一周用的时间=4÷
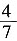
=7(小时)。
2. 将52个志愿者分成甲、乙两组参加义务植树活动,甲组植树150捆杨树苗,乙组植树200捆松树苗,假定甲、乙两组同时开始种植。
(1)根据历年统计,每名志愿者种植一捆杨树苗用时
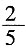
小时,种植一捆松树苗用时
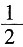
小时,应如何分配甲、乙两组的人数,才能使植树活动持续时间最短?
(2)在按(1)分配人数种植1小时后发现,每名志愿者种植一捆杨树苗的时间仍为
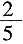
小时,而每名志愿者种植一捆松树苗的时间为
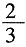
小时,于是从甲组抽调6名志愿者加入乙组继续种植,求本次活动所持续的时间。
(1)设甲组的人数为x,则乙组人数为52-x
甲组所用时间
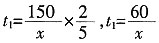
,
乙组所用时间
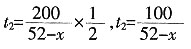
令t
1=t
2,则
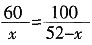
,解可得x=19.5
①当x=19时,t
1=
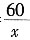
≈3.158,t2=
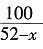
≈3.030<3.158,总用时3.158小时;
②当x=20时,
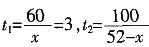
=3.125>3,总用时3.125小时。
所以应分配甲组20人,乙组32人,总用时最短为3.125小时。
(2)1小时后,甲组已种20÷
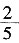
=50捆,余150-50=100捆杨树苗,此后,甲组20-6=14人,
还需100×
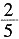
÷(20-6)=20÷7≈2.857小时
乙组已种32÷
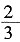
=48捆,余200-48=152捆,此后乙组32+6=38人
还需时间152×
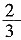
÷38=8÷3≈2.667小时<2.857小时
所以植树持续时间1+2.857=3.857小时。
三、案例分析题(本大题满分14分)1. 教学《有趣图形》时,教师首先让学生认识平面图形,在掌握平面图形后,教师安排了3个动手做一做的教学活动。
动手做一做(一):分组合作,让学生摸一摸,折一折,剪一剪,剪拼出一幅图案,并派代表介绍图案;(比一比,对优胜组及时表扬、奖励)
动手做一做(二):了解七巧板的组成,找出不同形状的图形,并用自己喜欢的颜色涂一涂;
动手做一做(三):放一首轻音乐,让学生一边放松,一边欣赏日常生活中的图案,看完后让学生说一说放了一些什么图案并说出它们的形状。
根据上述的案例,结合数教法的知识,说一说教师这样设计的价值和意义所在。
本教学片段以学生动手操作为主,使学生在操作中逐步加深对平面图形的认识,积累教学活动的经验,注重发展学生的空间观念。在动手做一做(一)中,为学生提供了表现的机会,发挥学生的想象力和创造力,创设了合作环境条件,发展了学生的合作意识。小组合作是一种行之有效的教育方式,利用组内合作,组间竞争的运行机制,使单向交流变成师生交流,这样不仅提高学生的主动性,也促进良好的人际关系。动手做一做(二)(三)既加深了学生对平面图形的认识,又进一步让学生感受了数学源于生活又回归生活的整个过程。整个过程,教师以学生为主体,让学生在整个课堂处于轻松的状态,激发学生爱动脑筋,并爱上学习数学的好习惯。
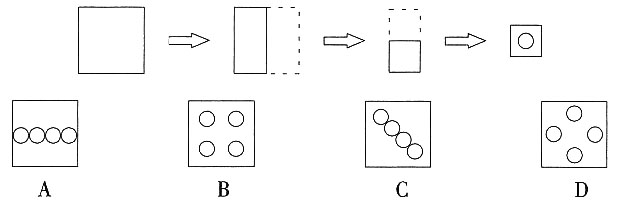
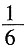 ,然后加满水,又喝了一杯的
,然后加满水,又喝了一杯的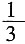 ,再倒满水后又喝了半杯,又加满了水,最后把一杯牛奶都喝了,那么李林喝的______。
,再倒满水后又喝了半杯,又加满了水,最后把一杯牛奶都喝了,那么李林喝的______。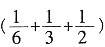 杯,即等于1杯,所以,李林喝的牛奶和水一样多。
杯,即等于1杯,所以,李林喝的牛奶和水一样多。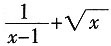 有意义,则实数x的取值范围是______。
有意义,则实数x的取值范围是______。
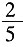 后,加满清水,再倒出
后,加满清水,再倒出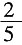 ,又加满清水,此时消毒液的浓度为______。
,又加满清水,此时消毒液的浓度为______。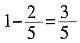 ,而溶液的量不变,则浓度也变为原来的
,而溶液的量不变,则浓度也变为原来的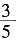 ,因此最后的浓度为20%×
,因此最后的浓度为20%×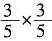 =7.2%。
=7.2%。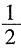 后得到线段CD,则端点C的坐标为______。
后得到线段CD,则端点C的坐标为______。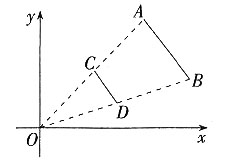
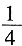 ,且样本容量为160,则中间一组的频数为______。
,且样本容量为160,则中间一组的频数为______。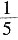 ,即
,即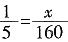 ,则x=32,选A。
,则x=32,选A。 =60种;4个都是奇数:
=60种;4个都是奇数: =5种。所以不同的取法共有66种。
=5种。所以不同的取法共有66种。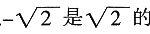 ______。
______。 的相反数。
的相反数。


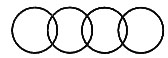
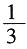
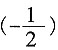 ×(-2)=1
×(-2)=1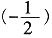 ×(-2)=1,此选项正确;C项,-(-1)0=-1,此选项错误;D项,|-2|=2,此选项错误。故选B。
×(-2)=1,此选项正确;C项,-(-1)0=-1,此选项错误;D项,|-2|=2,此选项错误。故选B。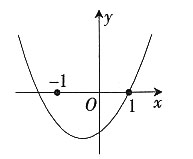
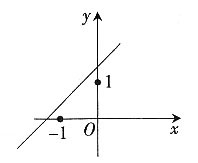
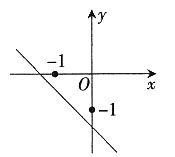
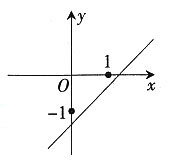
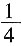 =0根的情况是______。
=0根的情况是______。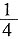 =0,故该方程有两个相等的实数根。
=0,故该方程有两个相等的实数根。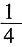

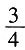
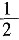 。
。
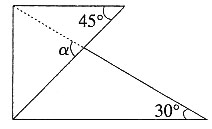
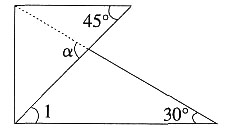

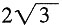
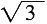
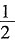 ∠CBA=30°,∴CE=BCtan30°=
∠CBA=30°,∴CE=BCtan30°=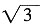 ,∴DE=2CE=
,∴DE=2CE=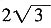 。故选C。
。故选C。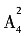 =12种;若第一道工序由乙来完成,则第四道工序必由甲、丙二人之一来完成,故完成方案共有
=12种;若第一道工序由乙来完成,则第四道工序必由甲、丙二人之一来完成,故完成方案共有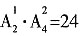 种;则不同的安排方案共有
种;则不同的安排方案共有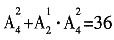 种。
种。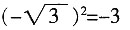
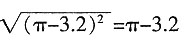
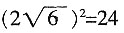
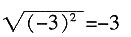
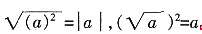 。
。

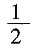
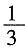
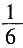
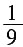
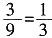 。故选B。
。故选B。
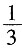
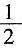
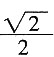
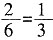 ,故选A。
,故选A。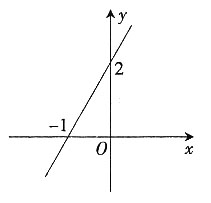
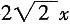 +1=0的两根,则代数式
+1=0的两根,则代数式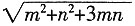 的值为______。
的值为______。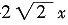 +1=0的两根,∴m+n=
+1=0的两根,∴m+n=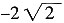 ,mn=1,
,mn=1,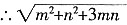 =
=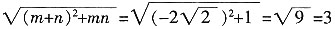 ,故选C。
,故选C。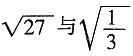 是同类二次根式
是同类二次根式 ,当x<0时,y随x的增大而增大
,当x<0时,y随x的增大而增大 =135°,故①正确;②
=135°,故①正确;②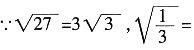
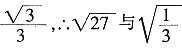 是同类二次根式;故②正确;③如图:∵OA=OB=AB,∴AOB=60°,∴∠C=
是同类二次根式;故②正确;③如图:∵OA=OB=AB,∴AOB=60°,∴∠C=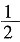 ∠AOB=30°,∴∠D=180°-∠C=150°,∴长度等于半径的弦所对的圆周角为30°或150°;故③错误;④反比例函数y=
∠AOB=30°,∴∠D=180°-∠C=150°,∴长度等于半径的弦所对的圆周角为30°或150°;故③错误;④反比例函数y=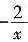 ,当x<0时,y随x的增大而增大。故④正确。故正确的有①②④,共3个,故选C。
,当x<0时,y随x的增大而增大。故④正确。故正确的有①②④,共3个,故选C。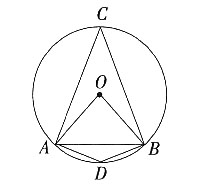
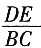 的值为______。
的值为______。
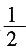
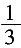
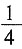
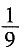
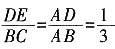 。
。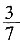 ,那么4小时就是行全程的
,那么4小时就是行全程的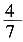 ,所以乙行一周用的时间=4÷
,所以乙行一周用的时间=4÷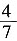 =7(小时)。
=7(小时)。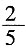 小时,种植一捆松树苗用时
小时,种植一捆松树苗用时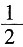 小时,应如何分配甲、乙两组的人数,才能使植树活动持续时间最短?
小时,应如何分配甲、乙两组的人数,才能使植树活动持续时间最短?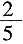 小时,而每名志愿者种植一捆松树苗的时间为
小时,而每名志愿者种植一捆松树苗的时间为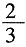 小时,于是从甲组抽调6名志愿者加入乙组继续种植,求本次活动所持续的时间。
小时,于是从甲组抽调6名志愿者加入乙组继续种植,求本次活动所持续的时间。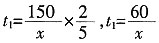 ,
,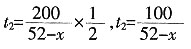
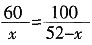 ,解可得x=19.5
,解可得x=19.5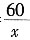 ≈3.158,t2=
≈3.158,t2=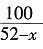 ≈3.030<3.158,总用时3.158小时;
≈3.030<3.158,总用时3.158小时;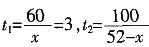 =3.125>3,总用时3.125小时。
=3.125>3,总用时3.125小时。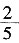 =50捆,余150-50=100捆杨树苗,此后,甲组20-6=14人,
=50捆,余150-50=100捆杨树苗,此后,甲组20-6=14人,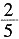 ÷(20-6)=20÷7≈2.857小时
÷(20-6)=20÷7≈2.857小时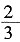 =48捆,余200-48=152捆,此后乙组32+6=38人
=48捆,余200-48=152捆,此后乙组32+6=38人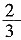 ÷38=8÷3≈2.667小时<2.857小时
÷38=8÷3≈2.667小时<2.857小时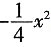 +2x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m。
+2x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m。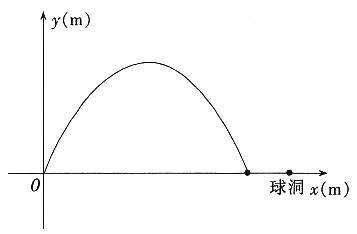
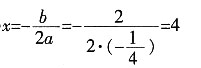
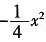 +2x得y=4
+2x得y=4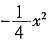 +2x=0
+2x=0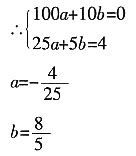
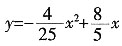 。
。
