银符考试题库B12
现在是:
试卷总分:150.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
 种
种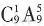 种
种 种
种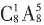 种
种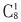 种结果。接着从9种不同的作物种子中选出5种放入5个不同的瓶子中展出,实际上是从9个元素中选5个排列,共有
种结果。接着从9种不同的作物种子中选出5种放入5个不同的瓶子中展出,实际上是从9个元素中选5个排列,共有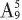 种结果。根据分步计数原理知共有
种结果。根据分步计数原理知共有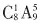 种结果。
种结果。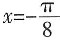 对称,则a=______。
对称,则a=______。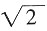
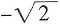
 。因为函数关于
。因为函数关于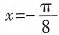 对称,所以
对称,所以 ,解得
,解得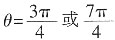 。由cos
。由cos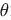 >0知
>0知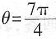 。即有
。即有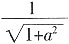 =
=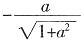 ,解得a=-1。
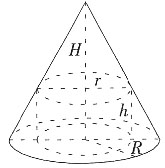
,解得a=-1。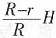 。圆柱侧面积
。圆柱侧面积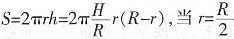 时,S有最大值。此时上边小圆锥的体积
时,S有最大值。此时上边小圆锥的体积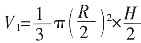 =
=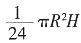 ,整个圆锥的体积V=
,整个圆锥的体积V=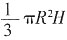 ,所以圆柱上底面将已知圆锥的体积分为大小两部分的比是
,所以圆柱上底面将已知圆锥的体积分为大小两部分的比是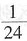 :
: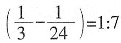 。
。
 的______。
的______。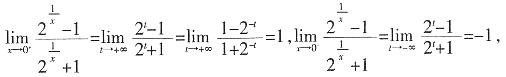
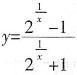 的跳跃间断点。
的跳跃间断点。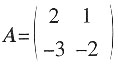 ,则A-1______。
,则A-1______。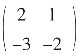 。
。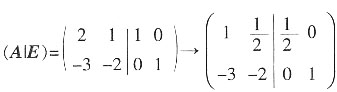 →
→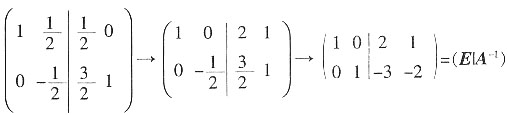 。所以
。所以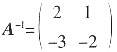 。
。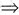 x2-2x+y2-6y=10……①,x2+y2=10……②,由①-②得到2x+6y=0
x2-2x+y2-6y=10……①,x2+y2=10……②,由①-②得到2x+6y=0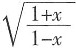 的奇偶性为______。
的奇偶性为______。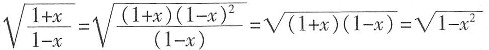 ,所以f(-x)=
,所以f(-x)=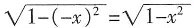 =f(x),所以函数f(x)为偶函数。
=f(x),所以函数f(x)为偶函数。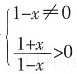 ,解得-1≤x<1,定义域不关于原点对称,所以此函数为非奇非偶函数。
,解得-1≤x<1,定义域不关于原点对称,所以此函数为非奇非偶函数。| 产品 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 | ||||||||||||||||||||||||||||||||||||||||||
| A产品 | 20 | m | 10 | 200 | ||||||||||||||||||||||||||||||||||||||||||
| B产品 | 40 | 8 | 18 | 120 | ||||||||||||||||||||||||||||||||||||||||||
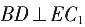 ;
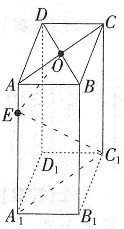
; E,A,C,C1共面
E,A,C,C1共面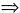 BD⊥面EACC1
BD⊥面EACC1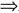 BD⊥EC1
BD⊥EC1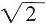 ,
,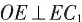 ,求AA1的长。
,求AA1的长。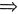 △OAE~△EA1C1
△OAE~△EA1C1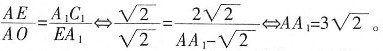
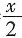 +sinx的所有正的极小值点从小到大排成的数列为{xn}。
+sinx的所有正的极小值点从小到大排成的数列为{xn}。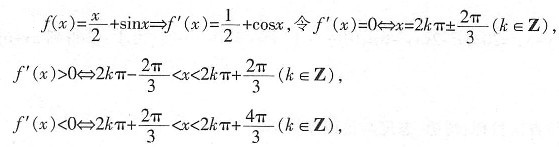
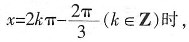 f(x)取极小值,
f(x)取极小值,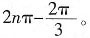
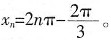
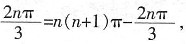
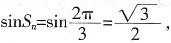

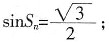
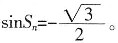
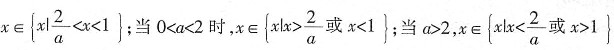 。
。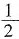 是整数
是整数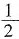 是整数吗?
是整数吗?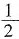
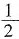 不是整数
不是整数