一、选择题(1~15小题为学科专业知识测试题,16~25小题为综合知识测试题)3. 在等腰△ABC中,AB=AC,AB的垂直平分线交AB于D,且经过点C,则下列结论中正确的是______。
A.△ADC是等腰三角形
B.△ABC是等边三角形
C.∠A=36°
D.AD=BD=
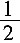
CD
A B C D
B
[解析] 根据线段的垂直平分线上的点到线段端点的距离相等可知,CA=CB,则AB=AC=BC,则△ABC是等边三角形。
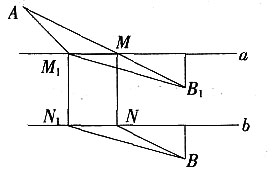
4. 如图,A和B两地在一条河的两岸,现要在河两岸造一座桥MN,使从A到B的路径AMNB最短的是______。
A.
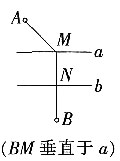
B.
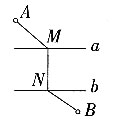
C.
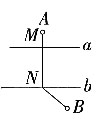
D.
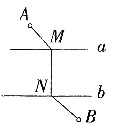
A B C D
D
[解析] 如下图中,桥MN的长度等于河宽,为定值。平移BN至B
1M,则显然当A、M、B
1在一条直线上时,AM+B
1M=AB
1最短,路径AMNB最短。其他情况下,A、M
1、B
1,构成三角形,AM
1+B
1M
1>AB
1。
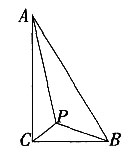
7. 在Rt△ABC中,已知∠C=90°,∠B=60°,BC=1,点P是△ABC内的一点,且∠APB=∠APC=∠CPB=120°,则AP+BP+CP=______。
A.
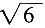
B.

C.
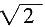
D.3
A B C D
B
[解析] 在下图中,∠PAB+∠PBA=180°-120°=60°,∠PBA+∠PBC=60°,则∠PAB=∠PBC,又∠APB=∠BPC=120°,则△PAB∽△PBC,则PA:PB=PB:PC=AB:BC=2:1。
设PC=x,则PB=2x,PA=4x。在△PCB中运用余弦定理,可解得x=
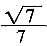
。则AP+BP+CP=7x=

。
9. 已知命题
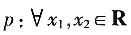
,(f(x
2)-f(x
1))(x
2-x
1)≥0,则
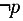
是______。
A.
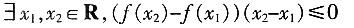
B.
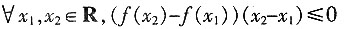
C.
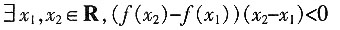
D.
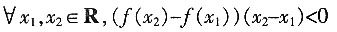
A B C D
C
[解析] 命题p为全称命题,所以其否定p应是特称命题,又f(x2)-f(x1))(x2-x1)≥0否定为(f(x2)-f(x1))(x2-x1)<0,故选C。
10. 已知数列{a
n}是公差为d的等差数列,S
n是其前n项和,且有S
9<S
8=S
7,则下列说法中不正确的是______。
- A.S9<S10
- B.d<0
- C.S7与S8均为Sn的最大值
- D.a8=0
A B C D
A
[解析] 由S9<S8=S7可知,a9<0,a8=0,故等差数列的首项a1>0,公差d<0,S7与S8均为Sn的最大值。而S=10=S9+a10,且a10=a9+d<a9<0,故必有S9>S10。所以选项A不正确。
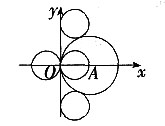
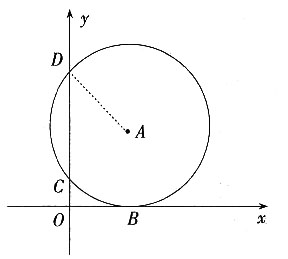
11. 如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴相切于点B,与y轴交于C(0,1),D(0,4)两点,则点A的坐标是______。
A.
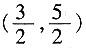
B.
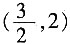
C.
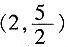
D.
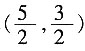
A B C D
C
[解析] 作AM⊥CD于M,则M为CD中点,CD=3,CM=
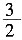
,OM=1+

,由于圆与x轴相切于点B,故圆的半径等于A的纵坐标的值,AB=OM=
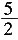
,在Rt△AMD中,求得AM=2,即为A点横坐标值,圆心坐标为
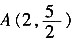
。
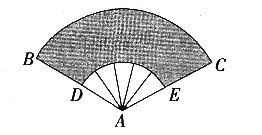
15. 如图,纸扇完全打开后,外侧两竹条AB、AC夹角为120°,AB的长为30cm,贴纸部分的长为20cm,则贴纸部分的面积为______。
A.100πcm
2 B.
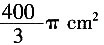
C.800πcm
2 D.
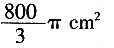
A B C D
D
[解析] 设AB=R,AD=r,则根据面积公式可得
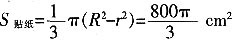
。
二、综合知识判断题1. 新疆生活着维吾尔、汉、哈萨克、回、蒙古等10个世居民族,各族人民结下了兄弟般的深厚情谊。
对 错
B
[解析] 新疆是一个多民族聚居地区,目前有47个民族。世居民族主要是维吾尔族、汉族、哈萨克族、回族、柯尔克孜族、蒙古族、锡伯族、俄罗斯族、塔吉克族、塔塔尔族、满族、达斡尔族等13个民族。
三、填空题1. 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=1:2,AE=2,则AC=______。
2. 设常数a>0,
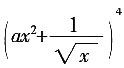
展开式中x
3的系数为
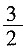
,则
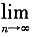
(a+a
2+…a
n=______。
1。
[解析]
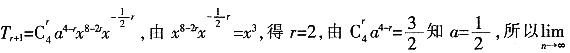
(a+a
2+…+a
n)=
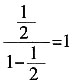
,所以为1。
3. 在

ABCD中,
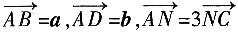
,M为BC的中点,则
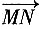
=______。(用a、b表示)。
4. 函数f(x)对于任意实数满足条件f(x+2)=
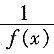
,若f(1)=-5,则f(f(5))=______。
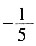
。
[解析] 由f(x+2)=
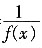
得f(x+4)=
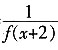
=f(x),所以f(5)=f(1)=-5,则f(f5))=f(-5)=f(-1)=
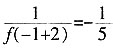
。
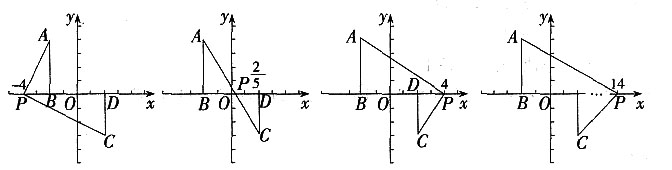
5. 在平面直角坐标系xOy中,已知点P(3,0),⊙P是以点P为圆心,2为半径的圆,若一次函数y=kx+b的图象过点A(-1,0)且与⊙P相切,则k+b的值为______。
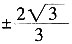
。
[解析] 由一次函数y=kx+b的图象过点A(-1,0)且与⊙P相切,可得到A(-1,0)在y=kx+b,并且P(3,0)到y=kx+b的距离为2。即
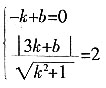
,解得k=b=
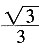
,因此k+b的值为
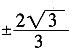
。
6. 分数单位是
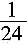
的分数中,大于
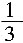
且小于
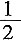
的最简分数的个数是______。
1。
[解析] 分数单位是

的分数中,大于
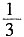
且小于
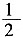
的分数共有
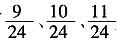
三个,其中最简分数只有
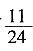
一个。
7. 一个由若干相同小正方体搭成的立体图形,从正面看是
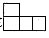
,从左面看是
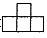
,要搭成这样的立体图形,则需要小正方体的个数至少是______。
8. 已知集合A=|x(x+1)(x-3)<0},B={x||x>2},则A∩B等于______。
{x|2<x<3}。
[解析] 集合A={x|-1<x<3},B={x+x<-2或x>2},则A∩B={x+2<x<3}。
9. 如图,一根电线杆的接线柱部分AB在阳光下的影子CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为______。
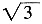
。
10.
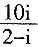
=______。
-2+4i。
[解析] 原式=

=-2+4i。
四、解答题(共45分)1. 计算:
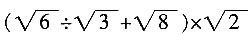
。
原式=
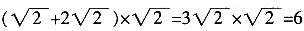
。
| 射击次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| 射中9环以上的次数 | 15 | 33 | | 63 | 79 | 97 | 111 | 130 |
| 射中9环以上的频率 | 0.75 | 0.83 | 0.80 | 0.79 | 0.79 | | 0.79 | 0.81 |
2. 根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
3. 根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由。
P=0.8,从频率的波动情况可以发现频率稳定在0.8附近,所以这名运动员射击一次时“射中9环以上”的概率是0.8。
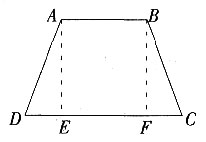
4. 若△DCF按顺时针方向旋转后恰好与△DAE重合,则旋转中心是点______;最少旋转了______度;
5. 在(1)的条件下,若AE=3,BF=2,求四边形BFDE的面积。
因为△DCF旋转后恰好与△DAE重合,
∴△DCF≌△DAE
∴AE=CF=3,又BF=2
∴BC=BF+CF=5
S四边形 BFDE=S△AED+S四边形 ABFD=S△DCF+S四边形 ABFD=S正方形 ABCD=BC2=25。
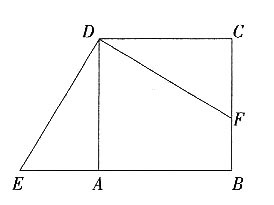
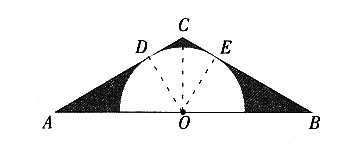
6. 如图,在△ABC中,∠C=120°,AC=BC,AB=4,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E。
(1)求半圆O的半径;
(2)求图中阴影部分的面积。
(1)连结OD、DE、OC,
∵半圆与AC、BC分别相切于点D、E。
∴OD⊥AC,OE⊥BC,且∠DCO=∠ECO。
∵AC=BC,
∴CO⊥AB且O是AB的中点。
∴AO=

AB=2。
∵∠C=120°,∴∠DCO=60°。
∴∠A=30°,
∴在Rt△AOD中,OD=
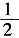
AO=1。
即半圆的半径为1。
(2)设CO=x,则在Rt△AOC中,因为∠A=30,所以AC=2x,由勾股定理得
AC
2-OC
2=AO
2,
即(2x)
2-x
2=2
2,
解得x=
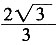
(x=
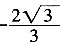
舍去),
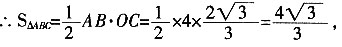
∵半圆的半径为1,
∴半圆的面积为
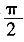
,
∴S
阴影=
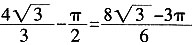
。
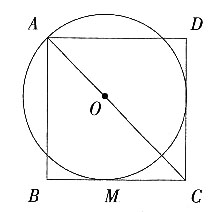
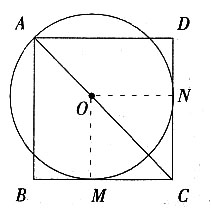
7. 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M。
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为1,求正方形ABCD的边长。
(1)过O作ON⊥CD于N,连结OM,则OM⊥BC。
∵AC是正方形ABCD的对角线,
∴AC是∠BCD的平分线。
∴OM=ON。
即圆心O到CD的距离等于⊙0半径,
∴CD与⊙O相切。
(2)由(1)易知△MOC为等腰直角三角形,OM为半径,
∴OM=MC=1
∴OC
2=OM
2+MC
2=1+1=2,
∴OC=
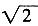
,
∴AC=AO+OC=1+
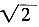
在Rt△ABC中,AB=BC,
由AC
2=AB
2+BC
2 ∴2AB
2=AC
2 ∴AB=
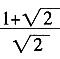
故正方形ABCD的边长为

。
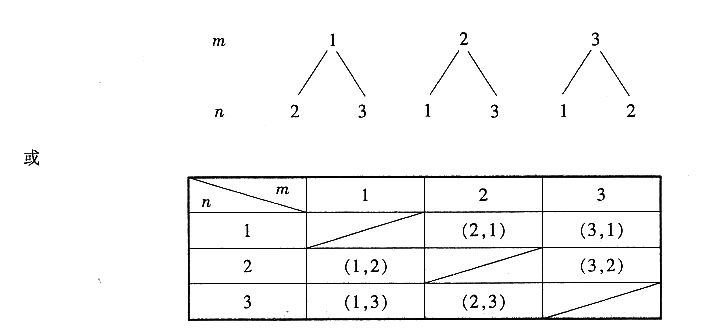
8. 请用树状图或者列表法,表示事件发生的所有可能情况;
9. 求关于x的方程x
2+mx+n=0有两个不相等实数根的概率。
当m
2-4n>0时,关于x的方程x
2+mx+n=0有两个不相等实数根,而使得m
2-4n>0的m、n有2组,即(3,1)和(3,2)。
则关于x的方程x
2+mx+n=0有两个不相等实数根的概率是
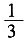
。
∴P(有两个不等实根)=
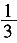
。
10. 已知关于x的方程
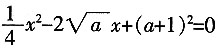
有实根。
(1)求a的值;
(2)若关于x的方程,mx
2+(1-m)x-a=0的所有根均为整数,求整数m的值。
(1)∵关于x的方程为
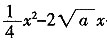
+(a+1)
2=0为一元二次方程,且有实根。
故满足:
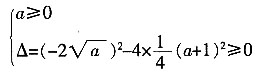
整理得:
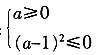
(2)由(1)可知a=1,
故(2)中的方程mx
2+(1-m)x-a=0可化为mx
2+(1-m)x-1=0
①当m=0时,原方程为x-1=0,根为x=1,符合题意;
②当m≠0时,mx
2+(1-m)x-1=0为关于x的一元二次方程。
△=(1-m)
2-4×m×(-1)=1-2m+m
2+4m=m
2+2m+1=(m+1)
2≥0,
此时,方程的两根为x
1=1,x
2=
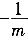
。
∵两根均为整数,
∴m=±1。
综上所述,m的值为-1,0或1。

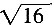 的算术平方根是______。
的算术平方根是______。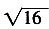 =4,4的算术平方根为2。
=4,4的算术平方根为2。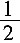 CD
CD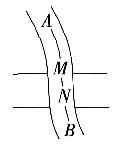






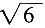

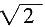
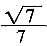 。则AP+BP+CP=7x=
。则AP+BP+CP=7x= 。
。
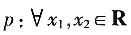 ,(f(x2)-f(x1))(x2-x1)≥0,则
,(f(x2)-f(x1))(x2-x1)≥0,则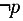 是______。
是______。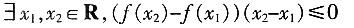
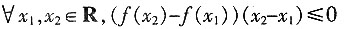
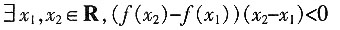
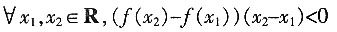
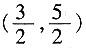
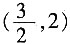
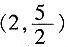
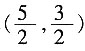
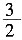 ,OM=1+
,OM=1+ ,由于圆与x轴相切于点B,故圆的半径等于A的纵坐标的值,AB=OM=
,由于圆与x轴相切于点B,故圆的半径等于A的纵坐标的值,AB=OM=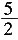 ,在Rt△AMD中,求得AM=2,即为A点横坐标值,圆心坐标为
,在Rt△AMD中,求得AM=2,即为A点横坐标值,圆心坐标为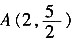 。
。
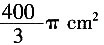
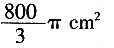
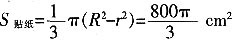 。
。
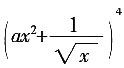 展开式中x3的系数为
展开式中x3的系数为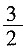 ,则
,则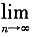 (a+a2+…an=______。
(a+a2+…an=______。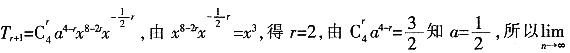 (a+a2+…+an)=
(a+a2+…+an)=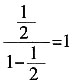 ,所以为1。
,所以为1。 ABCD中,
ABCD中,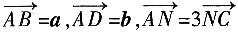 ,M为BC的中点,则
,M为BC的中点,则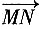 =______。(用a、b表示)。
=______。(用a、b表示)。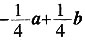 。
。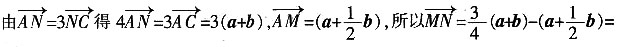
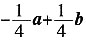 。
。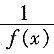 ,若f(1)=-5,则f(f(5))=______。
,若f(1)=-5,则f(f(5))=______。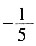 。
。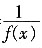 得f(x+4)=
得f(x+4)=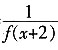 =f(x),所以f(5)=f(1)=-5,则f(f5))=f(-5)=f(-1)=
=f(x),所以f(5)=f(1)=-5,则f(f5))=f(-5)=f(-1)=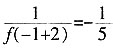 。
。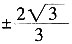 。
。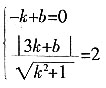 ,解得k=b=
,解得k=b=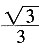 ,因此k+b的值为
,因此k+b的值为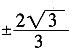 。
。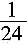 的分数中,大于
的分数中,大于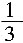 且小于
且小于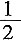 的最简分数的个数是______。
的最简分数的个数是______。 的分数中,大于
的分数中,大于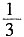 且小于
且小于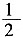 的分数共有
的分数共有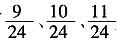 三个,其中最简分数只有
三个,其中最简分数只有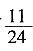 一个。
一个。 ,从左面看是
,从左面看是 ,要搭成这样的立体图形,则需要小正方体的个数至少是______。
,要搭成这样的立体图形,则需要小正方体的个数至少是______。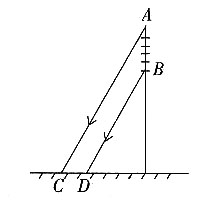
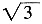 。
。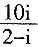 =______。
=______。 =-2+4i。
=-2+4i。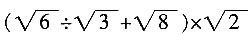 。
。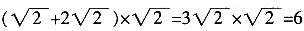 。
。
 AB=2。
AB=2。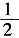 AO=1。
AO=1。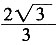 (x=
(x=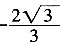 舍去),
舍去),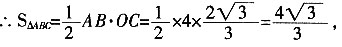
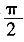 ,
,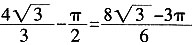 。
。
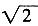 ,
,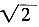
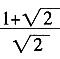
 。
。
 。
。 。
。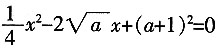 有实根。
有实根。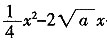 +(a+1)2=0为一元二次方程,且有实根。
+(a+1)2=0为一元二次方程,且有实根。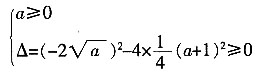
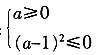
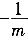 。
。