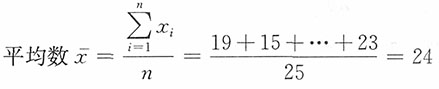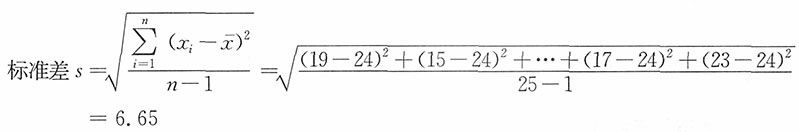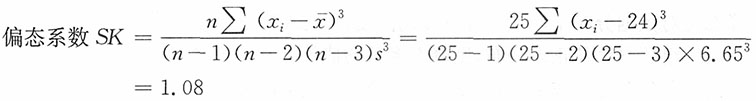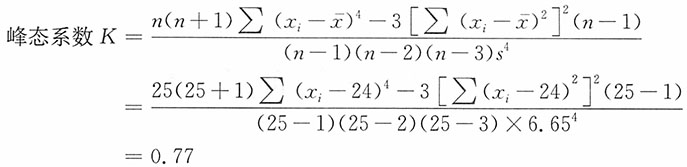银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
| 系统抽样 | |||||||||||||||||||||||||||||||||||||
| 存款金额(元) | 户数(户) | 存款金额(元) | 户数(户) | ||||||||||||||||||||||||||||||||||
| 1000以下 | 30 | 4000~5000 | 10 | ||||||||||||||||||||||||||||||||||
| 1000~2000 | 150 | 5000以上 | 10 | ||||||||||||||||||||||||||||||||||
| 2000~3000 | 250 | 合计 | 500 | ||||||||||||||||||||||||||||||||||
| 3000~4000 | 50 | ||||||||||||||||||||||||||||||||||||
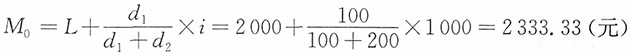 。
。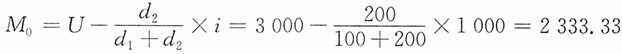 (元)。
(元)。| 生产某种零件日产量分组资料 | ||||||||||||||||||||||||||||
| 按日产量分组(件) | 工人数(人) | 向上累计 | ||||||||||||||||||||||||||
| 20 | 10 | 10 | ||||||||||||||||||||||||||
| 22 | 12 | 22 | ||||||||||||||||||||||||||
| 24 | 25 | 47 | ||||||||||||||||||||||||||
| 26 | 30 | 77 | ||||||||||||||||||||||||||
| 30 | 18 | 95 | ||||||||||||||||||||||||||
| 32 | 15 | 110 | ||||||||||||||||||||||||||
| 33 | 10 | 120 | ||||||||||||||||||||||||||
| 合计 | 120 | — | ||||||||||||||||||||||||||
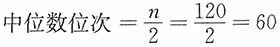 ,观察向上累计次数,首次超过60的是77,其对应组即为中位数组,由此中位数Me=26件。
,观察向上累计次数,首次超过60的是77,其对应组即为中位数组,由此中位数Me=26件。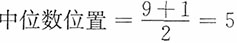 ,所以中位数为1080,即Me=1080(元)。
,所以中位数为1080,即Me=1080(元)。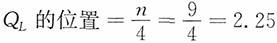 ,即QL在第2个数值(780)和第3个数值(850)之间0.25的位置上,因此QL=780+(850-780)×0.25=797.5(元)。
,即QL在第2个数值(780)和第3个数值(850)之间0.25的位置上,因此QL=780+(850-780)×0.25=797.5(元)。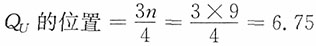 ,即QU在第6个数值(1250)和第7个数值(1500)之间0.75的位置上,因此QU=1250+(1500-1250)×0.75=1437.5(元)。
,即QU在第6个数值(1250)和第7个数值(1500)之间0.75的位置上,因此QU=1250+(1500-1250)×0.75=1437.5(元)。| 年龄分布数据 | |||||||||||||||||||||||||
| 15 16 17 18 19 | 19 19 20 20 21 | 22 22 23 23 23 | 24 24 25 27 29 | 30 31 34 38 41 | |||||||||||||||||||||

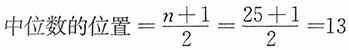 ,所以中位数=23。
,所以中位数=23。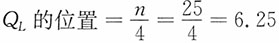 ,即QL第6个数值(19)和第7个数值(19)之间0.25的位置上,QL=19×0.75+19×0.25=19或QL=19+(19-19)×0.25=19。
,即QL第6个数值(19)和第7个数值(19)之间0.25的位置上,QL=19×0.75+19×0.25=19或QL=19+(19-19)×0.25=19。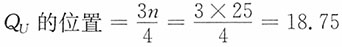 ,即QU在18个数值(25)和第19个数值(27)之间0.75的位置上,QU=25×0.25+27×0.75=26.5或QU=25+(27-25)×0.75=26.5。
,即QU在18个数值(25)和第19个数值(27)之间0.75的位置上,QU=25×0.25+27×0.75=26.5或QU=25+(27-25)×0.75=26.5。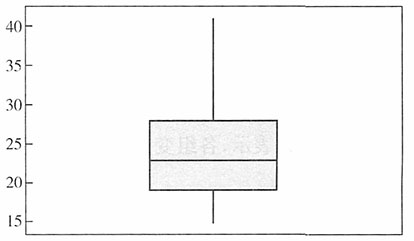
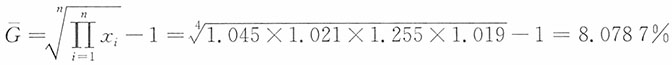
| 单位成本和总成本资料 | |||||||||||||||||||||||||||||
| 产品名称 | 单位成本 (元) | 总成本(元) | |||||||||||||||||||||||||||
| 甲企业 | 乙企业 | ||||||||||||||||||||||||||||
| A | 15 | 2100 | 3255 | ||||||||||||||||||||||||||
| B | 20 | 3000 | 1500 | ||||||||||||||||||||||||||
| C | 30 | 1500 | 1500 | ||||||||||||||||||||||||||

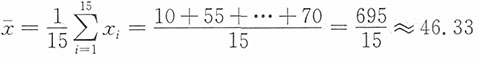 (分钟),众数Mo=25,30,40,55,70(分钟),中位数为第8个数值,Me=45(分钟)。其中均值最能反映这组数据的一般水平,因为均值是集中趋势的最主要测度值,且该组数据中不存在明显极端值,均值能较准确地反映这组数据的中心值。
(分钟),众数Mo=25,30,40,55,70(分钟),中位数为第8个数值,Me=45(分钟)。其中均值最能反映这组数据的一般水平,因为均值是集中趋势的最主要测度值,且该组数据中不存在明显极端值,均值能较准确地反映这组数据的中心值。
| 树茎 | 树叶 | 数据个数 | |||||||||||||||||
| 1 | 0 | 1 | |||||||||||||||||
| 2 | 55 | 2 | |||||||||||||||||
| 3 | 00 | 2 | |||||||||||||||||
| 4 | 005 | 3 | |||||||||||||||||
| 5 | 055 | 3 | |||||||||||||||||
| 6 | 0 | 1 | |||||||||||||||||
| 7 | 00 | 2 | |||||||||||||||||
| 9 | 0 | 1 | |||||||||||||||||
| 茎叶图 | |||||||||||||||||||

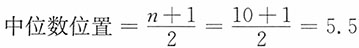 ,所以Me=10×0.5+10×0.5=10(台)。
,所以Me=10×0.5+10×0.5=10(台)。 。
。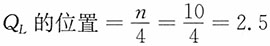 ,即QL第2个数值(4)和第3个数值(7)之间0.5的位置上,因此QL=4×0.5+7×0.5=5.5(台)。
,即QL第2个数值(4)和第3个数值(7)之间0.5的位置上,因此QL=4×0.5+7×0.5=5.5(台)。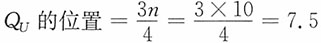 ,即QU在第7个数值(12)和第8个数值(12)之间0.5的位置上,因此QU=12×0.5+12×0.5=12(台)。
,即QU在第7个数值(12)和第8个数值(12)之间0.5的位置上,因此QU=12×0.5+12×0.5=12(台)。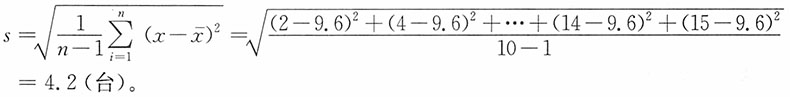
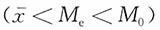 ,所以汽车销售量为左偏分布。
,所以汽车销售量为左偏分布。| 成绩频数分布 | |||||||||||||||||||||||||||||||||
| 分数(分) | 人数(人) | 分数(分) | 人数(人) | ||||||||||||||||||||||||||||||
| 60以下 | 4 | 80~90 | 7 | ||||||||||||||||||||||||||||||
| 60~70 | 8 | 90以上 | 0 | ||||||||||||||||||||||||||||||
| 70~80 | 13 | ||||||||||||||||||||||||||||||||
| 表1 乙班分数计算过程 | ||||||||||||||||||||||||||||
| 分数(分) | 组中值Mi | 人数(人)fi | Mifi | |||||||||||||||||||||||||
| 60分以下 | 55 | 4 | 220 | |||||||||||||||||||||||||
| 60~70 | 65 | 8 | 520 | |||||||||||||||||||||||||
| 70~80 | 75 | 13 | 975 | |||||||||||||||||||||||||
| 80~90 | 85 | 7 | 595 | |||||||||||||||||||||||||
| 90以上 | 95 | 5 | 475 | |||||||||||||||||||||||||
| 合计 | — | 37 | 2785 | |||||||||||||||||||||||||
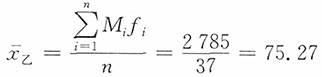
| 表2 方差计算过程 | |||||||||||||||||||||||||||||||||||||||||
| 分数(分) | 组中值Mi | 人数(人)fi | 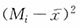
|
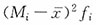
|
|||||||||||||||||||||||||||||||||||||
| 60分以下 | 55 | 4 | 410.873 | 1643.492 | |||||||||||||||||||||||||||||||||||||
| 60~70 | 65 | 8 | 105.473 | 843.783 | |||||||||||||||||||||||||||||||||||||
| 70~80 | 75 | 13 | 0.073 | 0.948 | |||||||||||||||||||||||||||||||||||||
| 80~90 | 85 | 7 | 94.673 | 662.710 | |||||||||||||||||||||||||||||||||||||
| 90以上 | 95 | 5 | 389.273 | 1946.365 | |||||||||||||||||||||||||||||||||||||
| 合计 | — | 37 | 1000.365 | 5097.298 | |||||||||||||||||||||||||||||||||||||
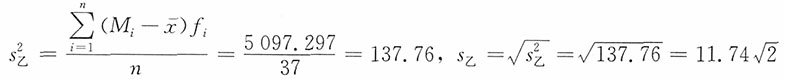
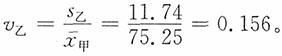
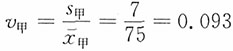 ,v甲<v乙,说明两个班的统计学考试成绩相比较,甲班的成绩较集中,乙班的成绩较分散。
,v甲<v乙,说明两个班的统计学考试成绩相比较,甲班的成绩较集中,乙班的成绩较分散。| 按人均收入水平分组 | |||||||||||||||||||||||||||||||||||||||||||||
| 按月收入水平分组(元) | 家庭数(户) | 按月收人水平分组(元) | 家庭数(户) | ||||||||||||||||||||||||||||||||||||||||||
| 400~600 | 20 | 1000以上 | 10 | ||||||||||||||||||||||||||||||||||||||||||
| 600~800 | 45 | 合计 | 100 | ||||||||||||||||||||||||||||||||||||||||||
| 800~1 000 | 25 | ||||||||||||||||||||||||||||||||||||||||||||
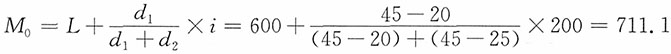
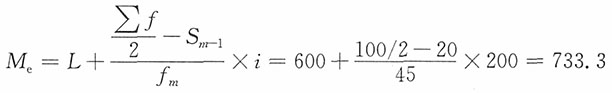
| 计算过程 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 按月收入 水平分组 |
组中值x | 家庭数f | xf | 
|
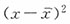
|
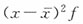
|
||||||||||||||||||||||||||||||||||||||||||||
| 400~600 | 500 | 20 | 10000 | -250 | 62500 | 1250000 | ||||||||||||||||||||||||||||||||||||||||||||
| 600~800 | 700 | 45 | 31500 | -50 | 2500 | 112500 | ||||||||||||||||||||||||||||||||||||||||||||
| 800~1000 | 900 | 25 | 22500 | 150 | 22500 | 562500 | ||||||||||||||||||||||||||||||||||||||||||||
| 1000以上 | 1100 | 10 | 11000 | 350 | 122500 | 1225000 | ||||||||||||||||||||||||||||||||||||||||||||
| 总计 | — | 100 | 75000 | — | — | 3150000 | ||||||||||||||||||||||||||||||||||||||||||||
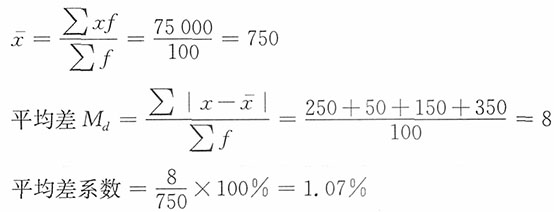
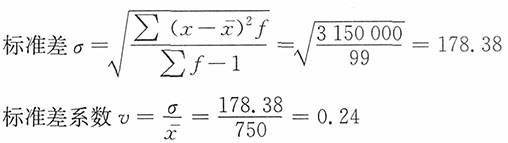
| 工资资料 | |||||||||||||||||||||||||||||||||||||||||
| 甲单位 | 乙单位 | ||||||||||||||||||||||||||||||||||||||||
| 月工资(元) | 职工人数(人) | 月工资(元) | 职工人数(人) | ||||||||||||||||||||||||||||||||||||||
| 600以下 | 2 | 600以下 | 1 | ||||||||||||||||||||||||||||||||||||||
| 600~700 | 4 | 600~700 | 2 | ||||||||||||||||||||||||||||||||||||||
| 700~800 | 10 | 700~800 | 4 | ||||||||||||||||||||||||||||||||||||||
| 800~900 | 7 | 800~900 | 12 | ||||||||||||||||||||||||||||||||||||||
| 900~1000 | 6 | 900~1000 | 6 | ||||||||||||||||||||||||||||||||||||||
| 1000~1100 | 4 | 1000~1100 | 5 | ||||||||||||||||||||||||||||||||||||||
| 合计 | 33 | 合计 | 30 | ||||||||||||||||||||||||||||||||||||||
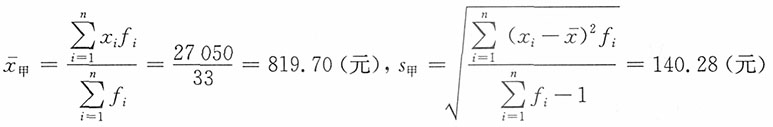
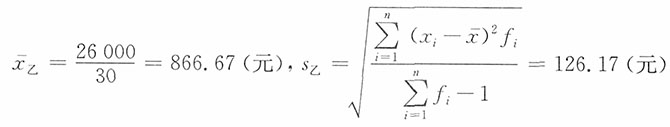
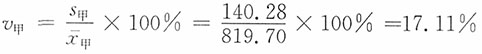 ,
, ,因为v甲>v乙,所以乙单位职工的工资差异程度小。
,因为v甲>v乙,所以乙单位职工的工资差异程度小。| 用户年龄数据 单位:周岁 | |||||||||||||||||||||||||
| 19 23 30 23 41 | 15 21 20 27 20 | 29 38 19 22 31 | 15 22 19 34 17 | 24 18 16 24 23 | |||||||||||||||||||||
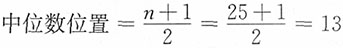 ,所以Me=23。
,所以Me=23。