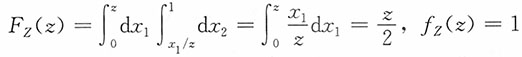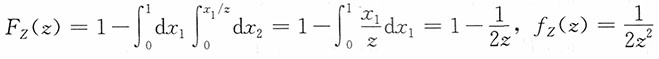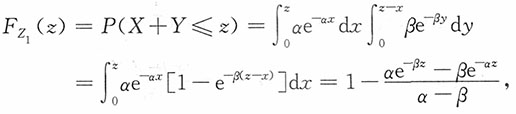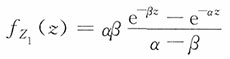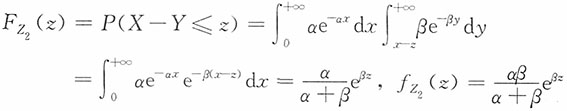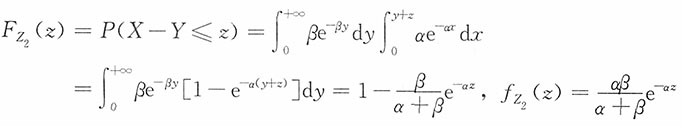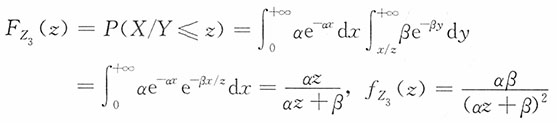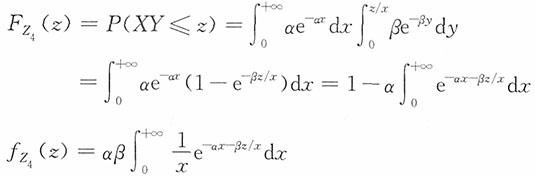计算题1. (辛普森分布)设X和Y独立,且
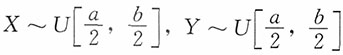
,求Z=X+Y的密度函数、分布函数。
解:当z<a时,F
Z(z)=0,fZ(z)=0
当
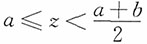
时,
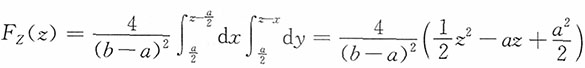
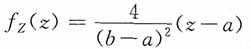
当
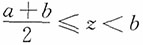
时,
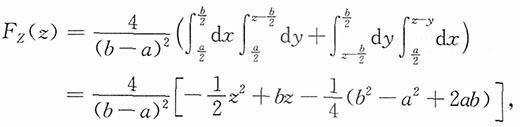
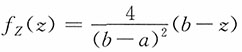
当z≥b时,F
Z(z)=1,f
Z(z)=0
特别地,如果取a=0,b=2,此时X~U[0,1],Y~U[0,1],如果X与Y相互独立,则Z=X+Y的分布函数、密度函数分别为
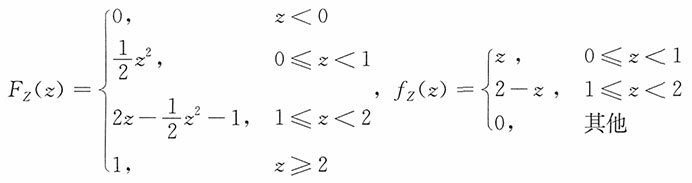
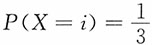 ,i=-1,0,1,而Y的密度函数为
,i=-1,0,1,而Y的密度函数为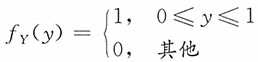 ,记Z=X+Y,求:
,记Z=X+Y,求:2.
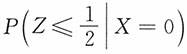
。
解:
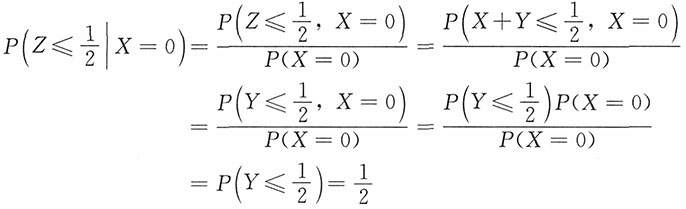
3. Z的密度函数。
解:当z<-1时,F
Z(z)=P(X+Y≤z)=0
当-1≤z<2时,
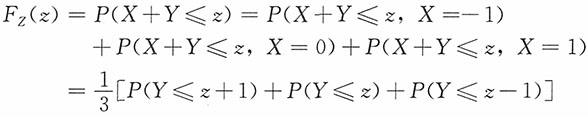
其中,当-1≤z<0时,P(Y≤z+1)=z+1,P(Y≤z)=0,P(Y≤z-1)=0
当0≤z<1时,P(Y≤z+1)=1,P(Y≤z)=z,P(Y≤z-1)=0
当1≤z<2时,P(Y≤z+1)=1,P(Y≤z)=1,P(Y≤z-1)=z-1
即,当-1≤z<0时,
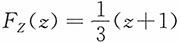
;当0≤z<1时,
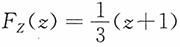
;当1≤z<2时,
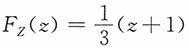
。
综上,
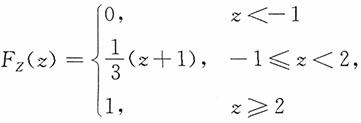
而密度函数
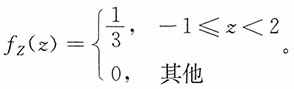
4. 设二维随机变量(X,Y)的联合密度函数为
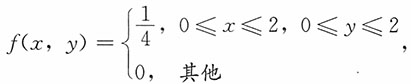
求:Z=X-Y的密度函数。
解:采用“分布函数法”,
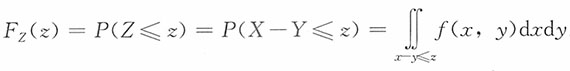
。
当z<-2时,F
Z(z)=0,f
Z(z)=0
当z≥2时,F
Z(z)=1,f
Z(z)=0
当-2≤z<0时,
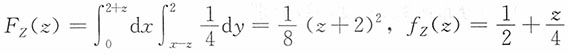
当0≤z<2时,
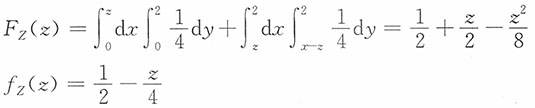
5. 设X和Y独立,且X~N(0,1),Y~N(0,1),求
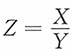
的密度函数。
解:对-∞<z<+∞,有
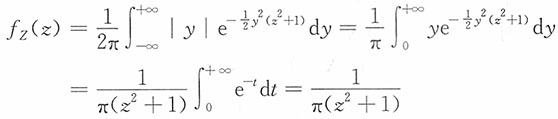
即Z服从标准柯西分布。
6. 设X,Y相互独立,其密度函数分别为
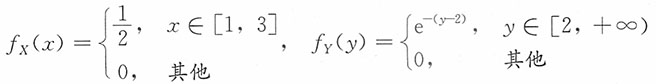
求
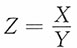
的密度函数。
7. 设X
1,X
2独立同服从U(0,1),求:Z=X
1X
2的密度函数。
解:当z<0时,F
Z(z)=0,f
Z(z)=0;当z≥1时,F
Z(z)=1,f
Z(z)=0
当0≤z<1时,
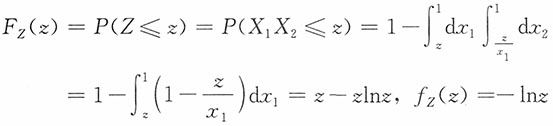
8. 设X
1,X
2,…,X
n独立同服从U(0,1),求
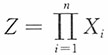
的密度函数。
解:当0<z<1时,
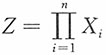
的密度函数为
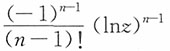
,可用数学归纳法给予证明。事实上,设
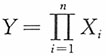
的密度函数为

,0<y<1,而X
n+1~U(0,1)且与Y相互独立。下面求Z=YX
n+1的密度函数。
对0<z<1,
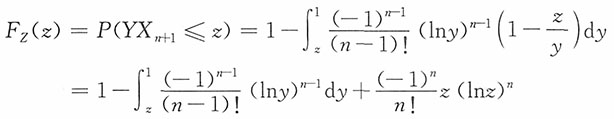
于是
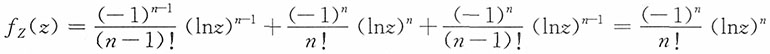
9. 设随机变量X,Y相互独立,且X~Exp(1),Y~Exp(1),证明X+Y和
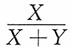
相互独立。
证明:由于X,Y相互独立同分布,(X,Y)的联合密度为f
X,Y(x,y)=e
-(x+y),x≥0,y≥0,令U=X+Y,

,作变换
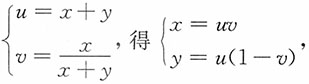
且当x≥0,y≥0时,u≥0,0≤v≤1,
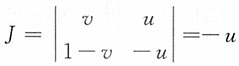
,|J|=u,故(U,V)的联合密度函数为f
U,V(u,v)=ue
-u,u≥0,0≤v≤1于是得U和V的边际密度函数f
U(u),f
V(v)
当u≥0时,
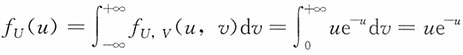
;当u<0时,f
U(u)=0
当0≤v≤1时,
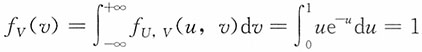
当v<0或v>1时,f
V(v)=0。
所以,f
U,V(u,v)=f
U(u)f
V(v),即U,V相互独立,亦即X+Y和
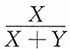
相互独立。
10. (瑞利分布)设火炮射2时弹着点的坐标(X,Y)服从二维正态分布,其联合密度函数为
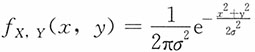
,此处把目标作为坐标原点,试求弹着点与目标之间的距离
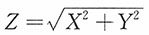
的密度函数f
Z(z)。
解:方法一:令
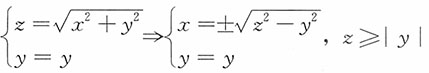
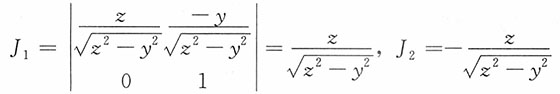
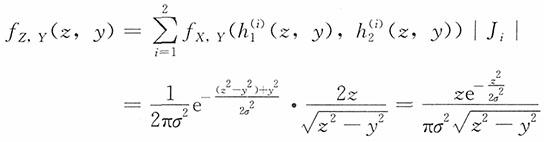
对z>0有
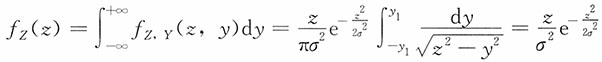
方法二:对z>0,
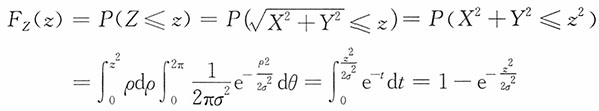
方法三:X~N(0,σ
2),Y~N(0,σ
2)且相互独立,则

,且相互独立。进而,
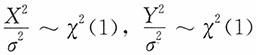
,且相互独立。于是有
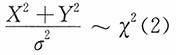
或Exp(1/2),所以,当z>0时,
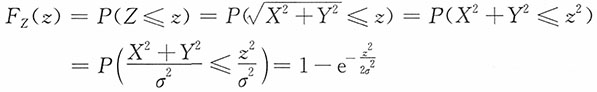
11. 设n个非负随机变量X
1,X
2,…,X
n独立同分布于指数分布Exp(λ),问X
(1)服从什么分布?
解:对x>0,FX(1)(x)=1-[1-F(x)]n=1-e-nλx,即X(1)~Exp(nλ)。
12. 设n个非负随机变量X
1,X
2,…,X
n独立同分布于两参数威布尔分布W(m,β),问X
(1)服从什么分布?
解:对x>0,
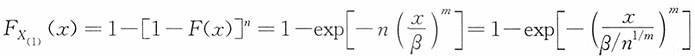
即

。
13. 设取值为正整数值的n个离散型随机变量X
1,X
2,…,X
n独立同分布于几何分布Ge(p),问X
(1)服从什么分布?
解:对k=1,2,…,
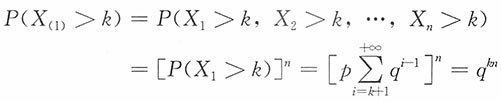
P(X
(1)=k)=P(X
(1)>k-1)-P(X
(1)>k)=q
(k-1)n-q
kn=(1-q
n)(q
n)
k-1 记p'=1-q
n,q'=1-p'=q
n,则P(X
(1)=k)=p'(q')
k-1,即X
(1)~Ge(p')。
14. 设X
1,X
2,…,X
n为连续型总体X的一个简单随机样本,记p
1=P(X
1>0),p
2=P(X
1+X
2>0),p
3=P(X
1+X
2>0,X
1>0)。请详细推导出用p
1,p
2表示p
3的关系式。
解:记总体X的密度函数与分布函数分别为f(x),F(x)。
A={X
1>0,X
2>0},B
1={X
1>0,X
2<0,X
1+X
2>0}
B
2={X
1>0,X
2<0,X
1+X
2<0},C={X
1<0,X
2>0,X
1+X
2>0}
A,B
1,B
2,C如图所示,则
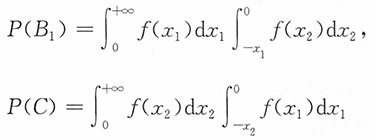
进而有P(B
1)=P(C)
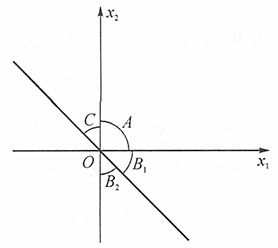 A,B,C图示
A,B,C图示 由于p
1=p
3+P(B
2),p
=p
3+P(C)=p
3+P(B
1)
而
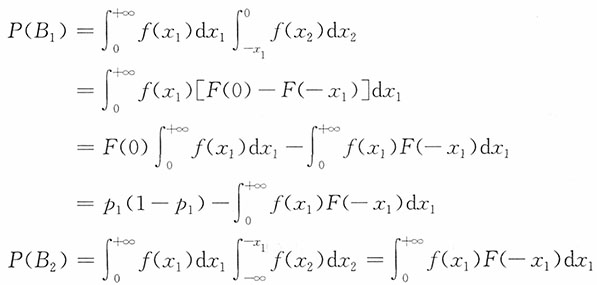
而p
1+p
2=2p
3+P(B
2)+P(B
1)=2p
3+p
1(1-p
1)
则
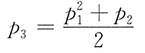
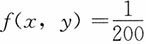 ,0≤x≤y,0≤y≤20。
,0≤x≤y,0≤y≤20。15. 给定Y=y条件下,X的条件分布。
解:Y的边际密度函数为
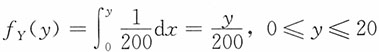
,于是
当0<y≤20时,有
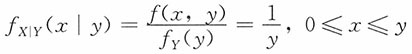
16. 假定某日开门时,Y=10(件)。求这天顾客买走X≤5(件)的概率,如果Y=20(件)呢?
解:因为
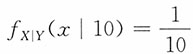
,0≤x≤10,所求概率
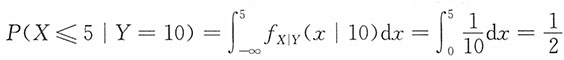
即开门营业时有10件货物,当日卖出不超过5件的概率为1/2。
又因为
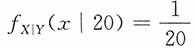
,0≤x≤20,于是
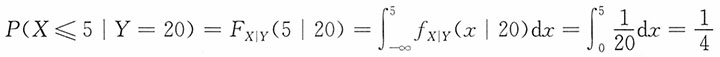
即开门营业时有20件货物,当日卖出不超过5件的概率仅为1/4。这表明货物销售量的概率与现有货物数量的关系很密切。
17. 设随机变量X有密度函数f
X(x)=λ
2xe
-λx,x>0,而随机变量Y在(0,X)上有均匀分布,求Y的密度函数f
Y(y)。
解:由于随机变量Y在(0,X)上有均匀分布,则
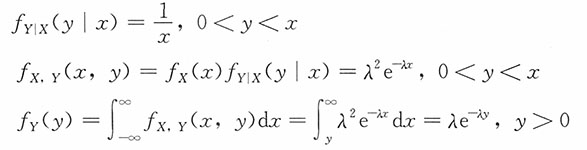
18. 设X和Y独立,且X服从[0,1]上的均匀分布,Y服从[0,2]上的辛普森分布,其分布密度函数为
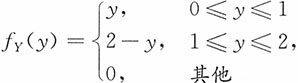
求Z=X+Y的密度函数。
解:采用“分布函数法”先求Z=X+Y的分布函数F
Z(z)。由于X和Y独立,则(X,Y)的联合密度函数为
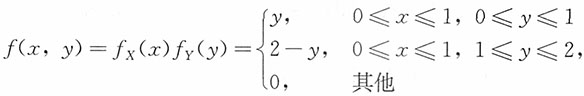
而f(x,y)在区域D
1={(x,y):0≤x≤1,0≤y≤1}和区域D
2={(x,y):0≤x≤1,1≤y≤2}上不为零。则
当z<0时,F
Z(z)=0,f
Z(z)=0
当z≥3时,F
Z(z)=1,f
Z(z)=0
当0≤z<1时,
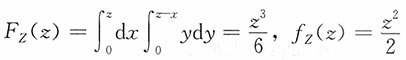
当1≤z<2时,
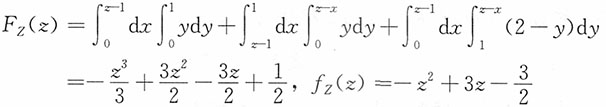
当2≤z<3时,
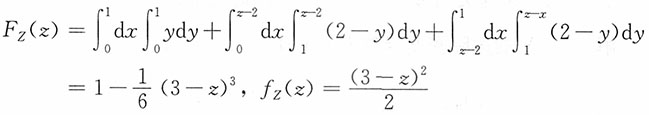
19. 设X与Y相互独立,且都服从标准正态分布N(0,1),令U=X
2+Y
2,
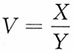
,求(U,V)的联合密度函数,并说明U和V是否独立?
解:由
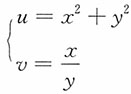
,得
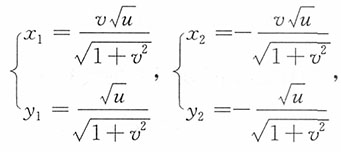
u>0,-∞<v<+∞
于是
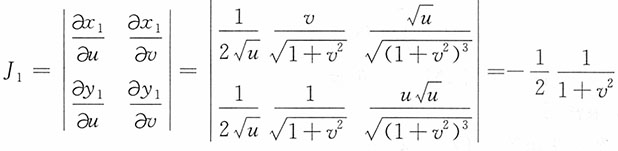
,
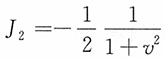
由于(X,Y)的联合密度函数为
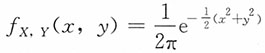
,-∞<x,y<+∞,则(U,V)联合密度函数为
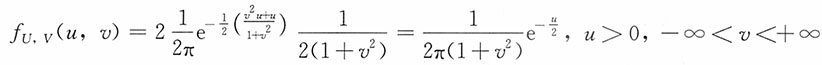
U的边际密度函数为
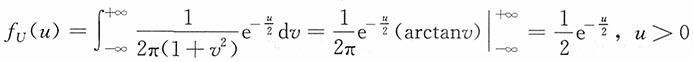
即
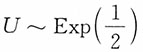
或χ
2(2),事实上可以从另一途径得到该结果。由于X,Y独立同服从N(0,1),则X
2~χ
2(1),Y
2~χ
2(1),进而X
2+Y
2~χ
2(2)。
V的边际密度函数为
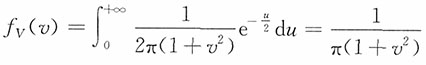
,-∞<v<+∞
即V服从标准柯西分布。
因此,f
U,V(u,v)=f
U(u)f
V(v),u>0,-∞<v<+∞,即随机变量U和V相互独立。
20. 设随机变量X和Y的联合概率密度函数为
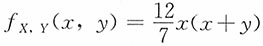
,0<x<1,0<y<1,令U=min(X,Y),V=max(X,Y),求U和V的联合密度函数。
解:方法一:将矩形{0<x<1,0<y<1}分为A和B两部分,如果随机点(X,Y)落入A,那么X<Y;如果随机点(X,Y)落入B,那么X>Y。对区域A,随机变量的变换成为
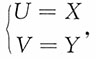
此时密度函数中变量的变换和逆变换分别为
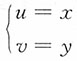
和

0<u<v<1,变换的雅可比行列式为
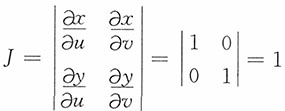
。而对区域B,随机变量的变换成为
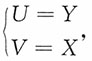
此时密度函数中变量的变换和逆变换分别为
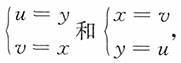
0<u<v<1,变换的雅可比行列式为
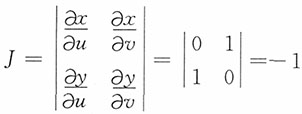
。于是,U和V的联合密度函数为
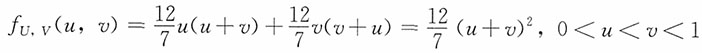
方法二:对0<u,v<1,
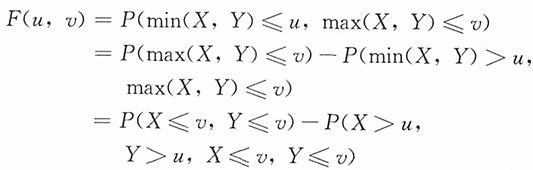
当u≥v时,
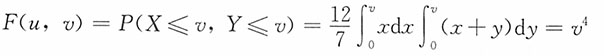
当u<v时,
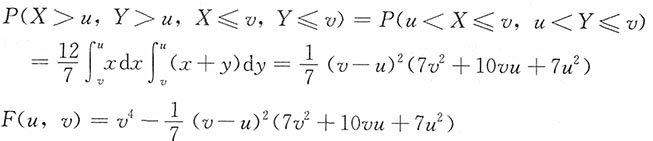
由此,当0<u<v<1时,
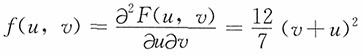
。
21. 已知随机变量X与Y相互独立,X服从参数为λ的指数分布,P(Y=-1)=0.25,P(Y=1)=0.75,试计算概率P(X-Y≤1);P(XY≤2)。
解:
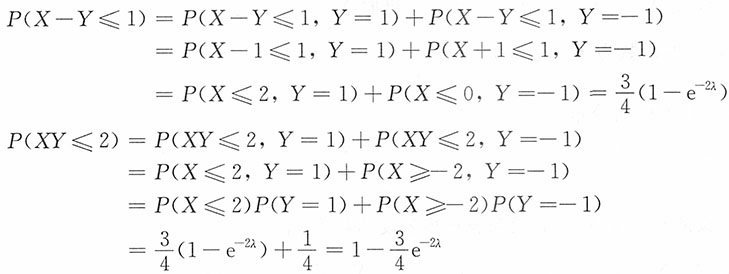
22. 设随机变量X,Y,Z的联合密度函数为
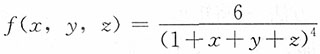
,x,y,z>0,求X+Y+Z的密度函数。
解:记T=X+Y+Z,则对t>0有
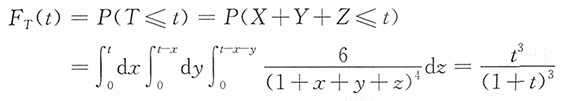
则有
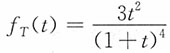
23. 设X
1,X
2独立同服从U(0,1),求(1)Z=X
1-X
2的密度函数。
解:当z<0,
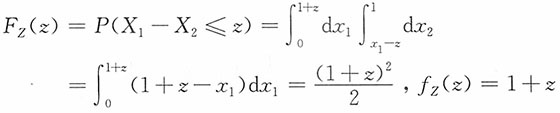
当z>0时,

24. 求
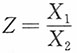
的密度函数。
解:当z<1时,
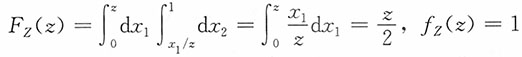
当z≥1时,
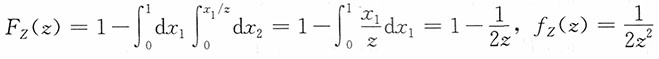
25. 设独立的随机变量X,Y分别服从参数为α,β的指数分布,分别求Z
1=X+Y,Z
2=X-Y,Z
3=X/Y和Z
4=XY的密度函数。
解:(1)当z>0时,
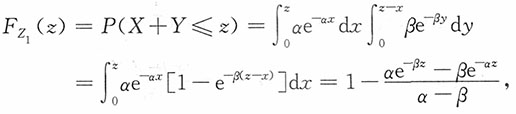
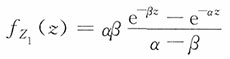
特别地,若α=β,则F
Z1(z)=1-e
-αz-αze
-αz,f
Z1(z)=α
2ze
-αz (2)当z<0时,
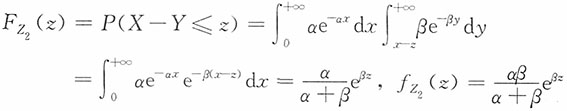
当z>0时,
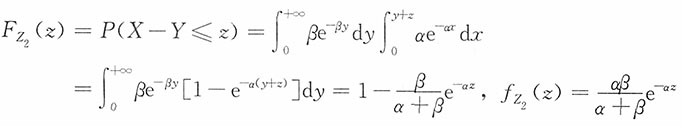
(3)当z>0时,
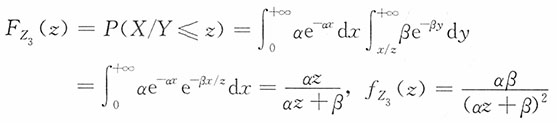
(4)当z>0时,
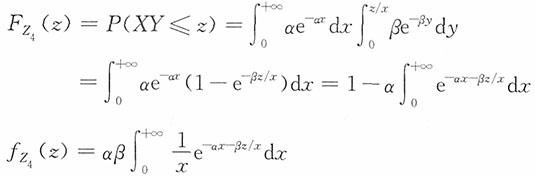
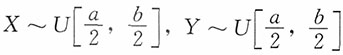 ,求Z=X+Y的密度函数、分布函数。
,求Z=X+Y的密度函数、分布函数。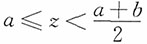 时,
时,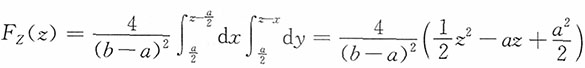
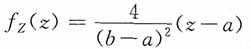
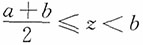 时,
时,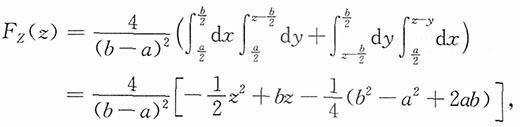
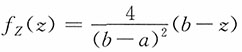
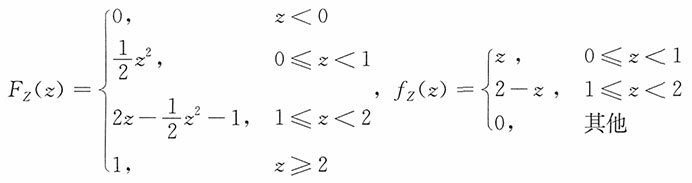
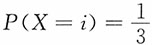 ,i=-1,0,1,而Y的密度函数为
,i=-1,0,1,而Y的密度函数为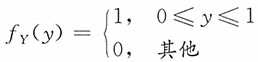 ,记Z=X+Y,求:
,记Z=X+Y,求: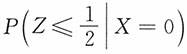 。
。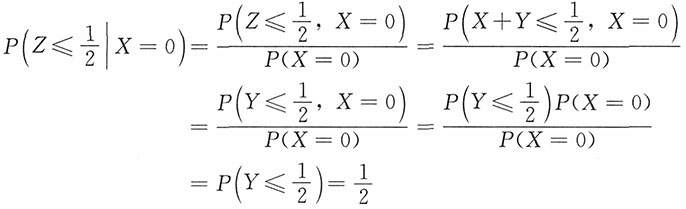
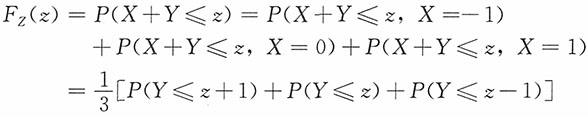
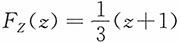 ;当0≤z<1时,
;当0≤z<1时,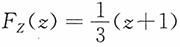 ;当1≤z<2时,
;当1≤z<2时,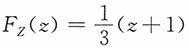 。
。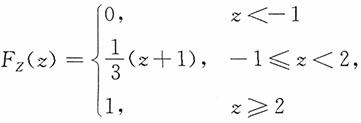 而密度函数
而密度函数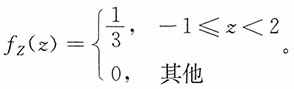
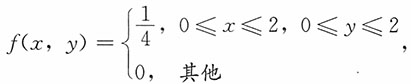 求:Z=X-Y的密度函数。
求:Z=X-Y的密度函数。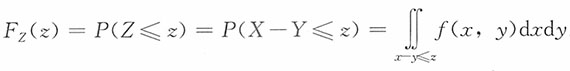 。
。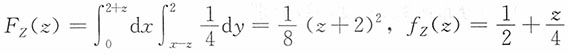
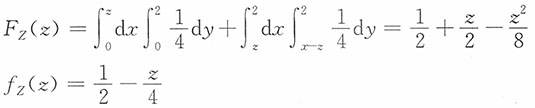
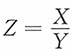 的密度函数。
的密度函数。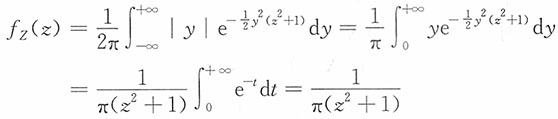
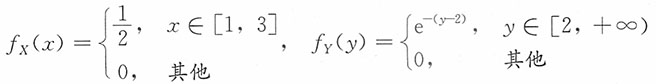
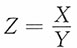 的密度函数。
的密度函数。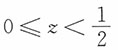 时,
时,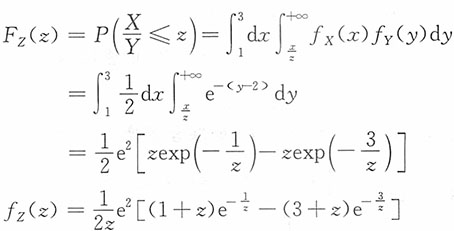
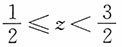 时,
时,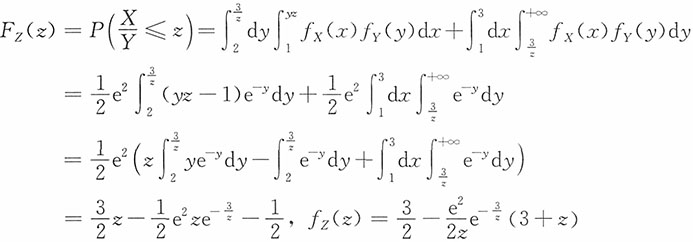
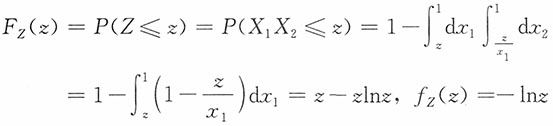
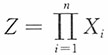 的密度函数。
的密度函数。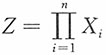 的密度函数为
的密度函数为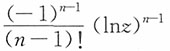 ,可用数学归纳法给予证明。事实上,设
,可用数学归纳法给予证明。事实上,设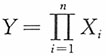 的密度函数为
的密度函数为 ,0<y<1,而Xn+1~U(0,1)且与Y相互独立。下面求Z=YXn+1的密度函数。
,0<y<1,而Xn+1~U(0,1)且与Y相互独立。下面求Z=YXn+1的密度函数。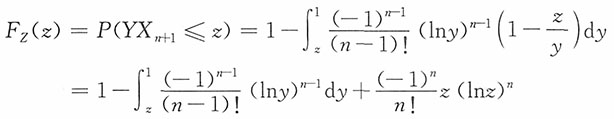
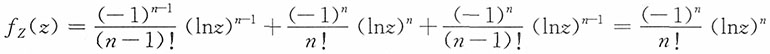
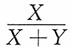 相互独立。
相互独立。 ,作变换
,作变换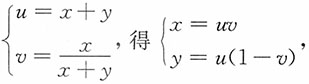 且当x≥0,y≥0时,u≥0,0≤v≤1,
且当x≥0,y≥0时,u≥0,0≤v≤1,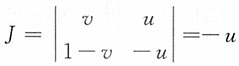 ,|J|=u,故(U,V)的联合密度函数为fU,V(u,v)=ue-u,u≥0,0≤v≤1于是得U和V的边际密度函数fU(u),fV(v)
,|J|=u,故(U,V)的联合密度函数为fU,V(u,v)=ue-u,u≥0,0≤v≤1于是得U和V的边际密度函数fU(u),fV(v)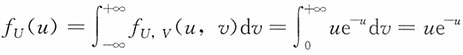 ;当u<0时,fU(u)=0
;当u<0时,fU(u)=0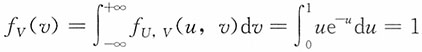
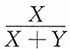 相互独立。
相互独立。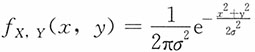 ,此处把目标作为坐标原点,试求弹着点与目标之间的距离
,此处把目标作为坐标原点,试求弹着点与目标之间的距离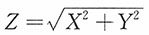 的密度函数fZ(z)。
的密度函数fZ(z)。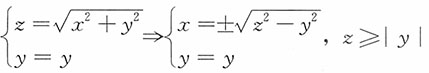
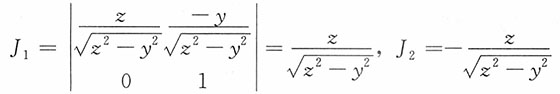
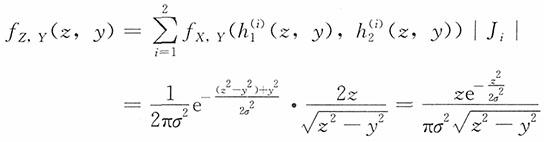
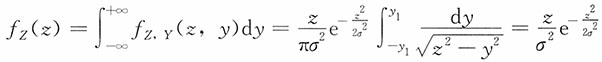
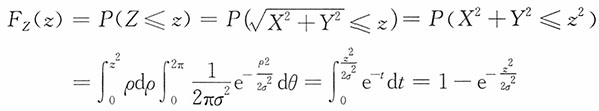
 ,且相互独立。进而,
,且相互独立。进而,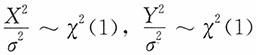 ,且相互独立。于是有
,且相互独立。于是有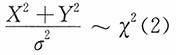 或Exp(1/2),所以,当z>0时,
或Exp(1/2),所以,当z>0时,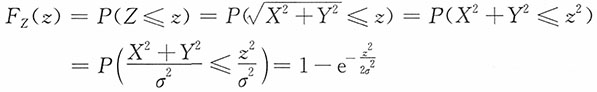
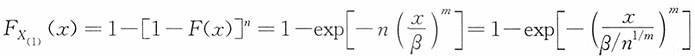 即
即 。
。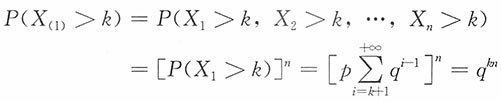
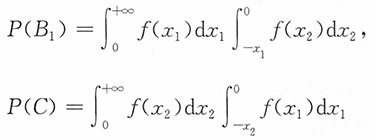

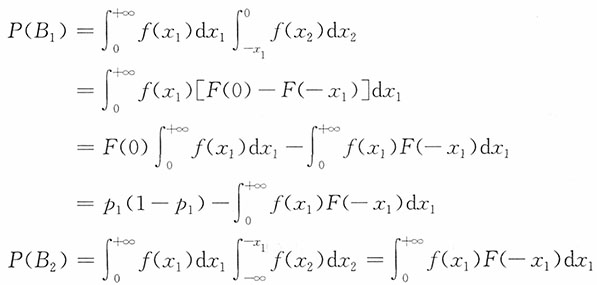
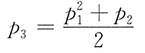
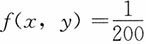 ,0≤x≤y,0≤y≤20。
,0≤x≤y,0≤y≤20。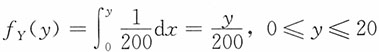 ,于是
,于是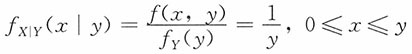
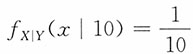 ,0≤x≤10,所求概率
,0≤x≤10,所求概率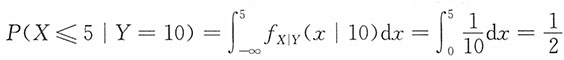
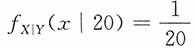 ,0≤x≤20,于是
,0≤x≤20,于是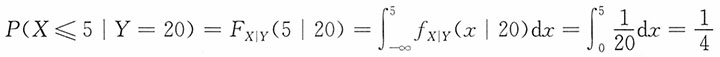
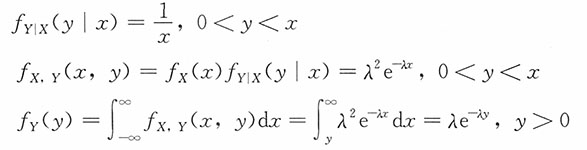
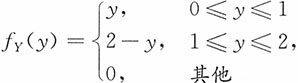 求Z=X+Y的密度函数。
求Z=X+Y的密度函数。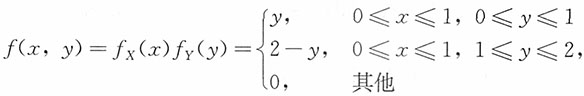 而f(x,y)在区域D1={(x,y):0≤x≤1,0≤y≤1}和区域D2={(x,y):0≤x≤1,1≤y≤2}上不为零。则
而f(x,y)在区域D1={(x,y):0≤x≤1,0≤y≤1}和区域D2={(x,y):0≤x≤1,1≤y≤2}上不为零。则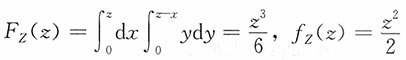
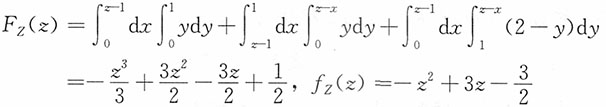
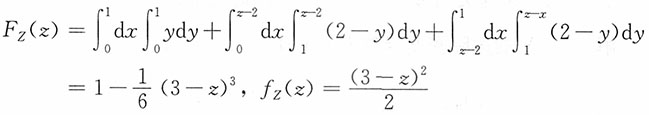
 ,求(U,V)的联合密度函数,并说明U和V是否独立?
,求(U,V)的联合密度函数,并说明U和V是否独立?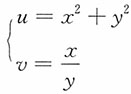 ,得
,得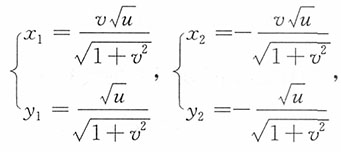 u>0,-∞<v<+∞
u>0,-∞<v<+∞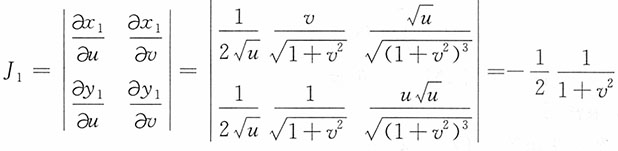 ,
,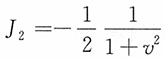
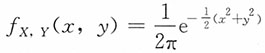 ,-∞<x,y<+∞,则(U,V)联合密度函数为
,-∞<x,y<+∞,则(U,V)联合密度函数为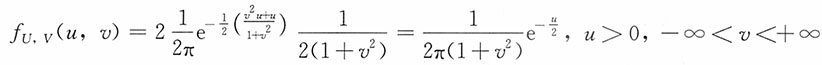
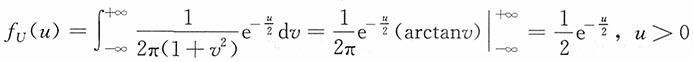
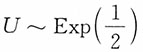 或χ2(2),事实上可以从另一途径得到该结果。由于X,Y独立同服从N(0,1),则X2~χ2(1),Y2~χ2(1),进而X2+Y2~χ2(2)。
或χ2(2),事实上可以从另一途径得到该结果。由于X,Y独立同服从N(0,1),则X2~χ2(1),Y2~χ2(1),进而X2+Y2~χ2(2)。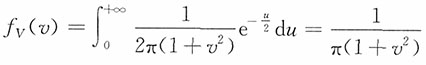 ,-∞<v<+∞
,-∞<v<+∞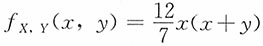 ,0<x<1,0<y<1,令U=min(X,Y),V=max(X,Y),求U和V的联合密度函数。
,0<x<1,0<y<1,令U=min(X,Y),V=max(X,Y),求U和V的联合密度函数。 此时密度函数中变量的变换和逆变换分别为
此时密度函数中变量的变换和逆变换分别为 和
和 0<u<v<1,变换的雅可比行列式为
0<u<v<1,变换的雅可比行列式为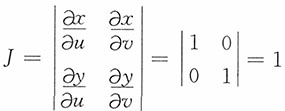 。而对区域B,随机变量的变换成为
。而对区域B,随机变量的变换成为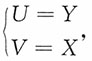 此时密度函数中变量的变换和逆变换分别为
此时密度函数中变量的变换和逆变换分别为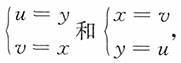 0<u<v<1,变换的雅可比行列式为
0<u<v<1,变换的雅可比行列式为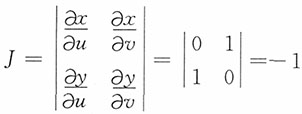 。于是,U和V的联合密度函数为
。于是,U和V的联合密度函数为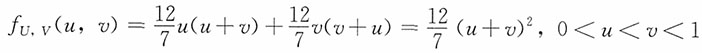
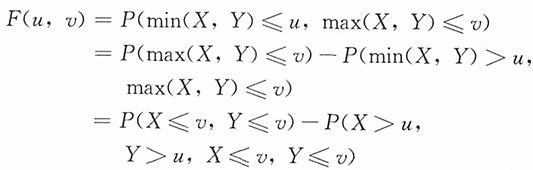
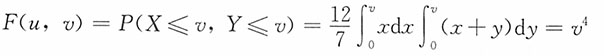
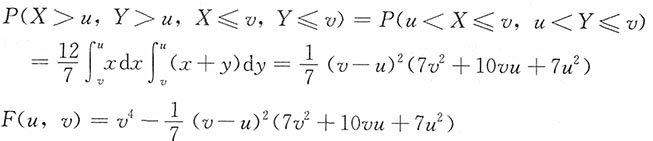
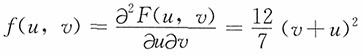 。
。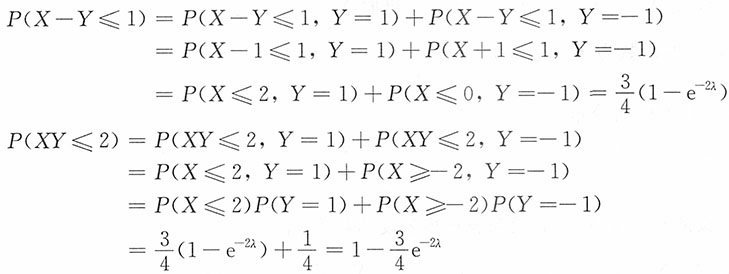
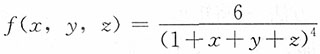 ,x,y,z>0,求X+Y+Z的密度函数。
,x,y,z>0,求X+Y+Z的密度函数。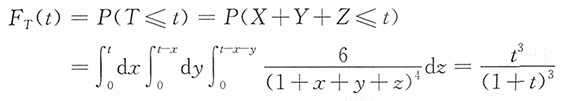
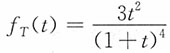
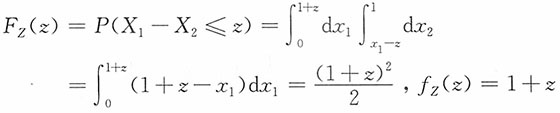

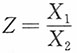 的密度函数。
的密度函数。