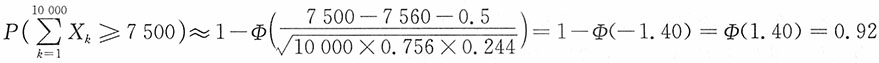单项选择题8. 已知随机变量X服从正态分布N(μ,σ
2)设随机变量Y为X的指数函数,即Y=e
X,则Y的期望值为______。
A.μ+σ
2 B.
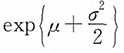
C.
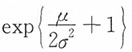
D.exp{μ}
A B C D
B
[解析] 该题事实上是对数正态分布的k阶矩。若X~N(μ,σ
2),则Y=e
X~LN(μ,σ
2)。
令

,Y=eX=e
μe
σZ,则
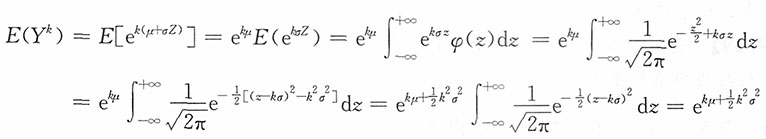
特别地
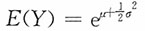
10. 设X
1,X
2,…,X
n,…是相互独立的随机变量,X
n服从参数为n的指数分布n≥1,则下列随机变量序列中不服从车贝雪夫大数定律的是______。
A.
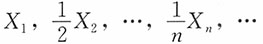
B.X
1,X
2,…,X
n,…
C.X
1,2X
2,…,nX
n,…
D.X
1,2
2X
2,…,n
2X
n,…
A B C D
12. 设随机变量X
1,X
2,…,X
n相互独立,S
n=X
1+X
2+…+X
n,则根据列维—林德伯格中心极限定理,当n充分大时,S
n近似服从正态分布,只要X
1,X
2,…,X
n______。
- A.有相同的期望和方差
- B.服从同一离散型分布
- C.服从同一指数分布
- D.服从同一连续型分布
A B C D
C
[解析] 列维—林德伯格中心极限定理的条件是:随机变量X1,X2,…,Xn相互独立同分布,并且其数学期望和方差存在。由于有相同的数学期望和方差未必有相同分布,可见A不满足定理条件。满足B和D的随机变量Xi的数学期望或方差未必存在,故B和D也不满足定理条件。于是只有C成立。
14. 设随机变量序列X
1,X
2,…,X
n,…,记
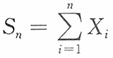
(n足够大),则S
n可用正态分布近似的充分条件是______。
A.X
1,X
2,…,X
n,…独立同分布,且概率密度均为
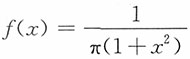
B.X
1,X
2,…,X
n,…均服从参数为λ的泊松分布
C.X
1,X
2,…,X
n,…相互独立,都服从区间[a,b]上的均匀分布
D.X
1,X
2,…,X
n,…均服从参数为p,0<p<1的两点分布
A B C D
C
[解析] 适用中心极限定理的条件是X1,X2,…,Xn,…独立同分布,且期望与方差均存在,B,D缺独立的条件,而A的期望不存在,故选C。
15. 设随机变量X
1,X
2,…,X
n独立同分布,且X
i有概率密度f
i(x),记
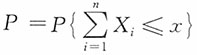
,当”充分大时,有______。
- A.P可以根据fi(x),i=1,2,…,n计算
- B.P不可以根据fi(x),i=1,2,…,n计算
- C.P一定可以根据中心极限定理计算
- D.P一定不能根据中心极限定理计算
A B C D
A
[解析]
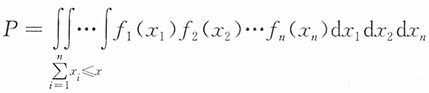
,而题中并未明确X
i的期望与方差是否存在,故不能用中心极限定理计算,选A。
计算题若随机变量X的密度函数为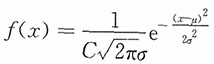 ,x≥0,C>0,σ>0,则称X服从截尾正态分布,记标准正态密度
,x≥0,C>0,σ>0,则称X服从截尾正态分布,记标准正态密度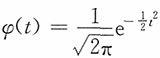 ,分布函数为Φ(t),请回答下列问题:
,分布函数为Φ(t),请回答下列问题:1. 求常数C的值(用μ,σ,φ,Φ表示)。
解:
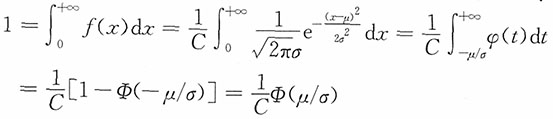
得C=Φ(μ/σ)
2. 求随机变量X的期望(用μ,σ,φ,Φ表示)。
3. 求随机变量X的方差(注:该小题积分是积不出的)。
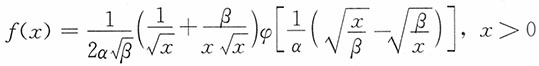
其中,α>0称为形状参数,β>0称为刻度参数,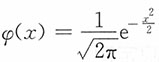 。
。4. 求X的分布函数。
解:当x>0时,
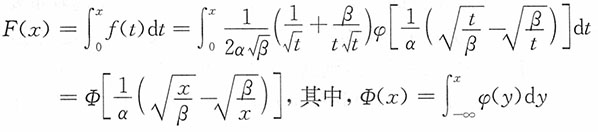
5. 求E(X),D(X)及变异系数。
解:记
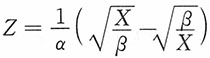
,由(1)易见Z~N(0,1),又
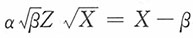
,
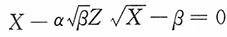
,
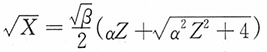
进而

又由于E(Z
2)=1,E(Z
4)=3,同时考虑到被积函数是奇函数,则有
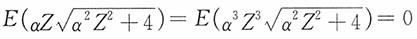
则
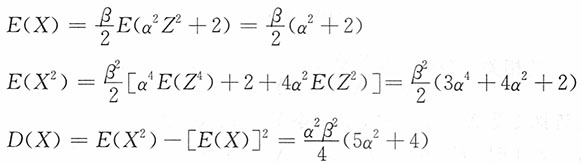
变异系数为
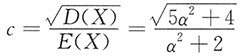
6. 设x≥0为随机变量,证明
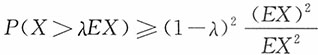
,0<λ<1
证明:构造示性函数
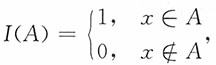
则
EX=E[XI(X>λEX)]+E[XI(X≤λEX)]
E[XI(X≤λEX)]≤λE(X)E[I(X≤λEX)]=λE(X)P(X≤λEX)≤λEX
由柯西-许瓦兹不等式:
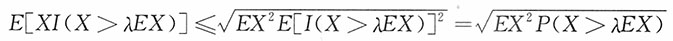
由此
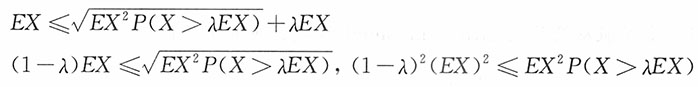
则
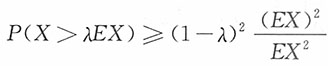
7. 若{X
n,n=1,2,…}是相互独立的随机变量序列,对每个n,X
n的分布列为
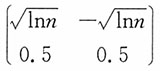
,问{X
n,n=1,2,…}是否服从马尔科夫大数定律?
解:E(X
n)=0,
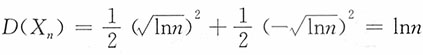
,而
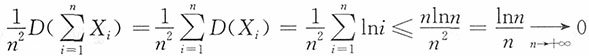
,于是马尔可夫大数定律成立。
8. 若{X
n,n=1,2,…}是相互独立的随机变量序列,对每个n,X
n的分布列为
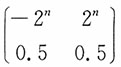
,问马尔可夫条件是否成立?
解:E(X
n)=0,
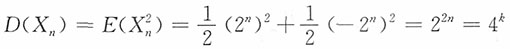
,而
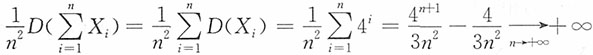
,故马尔可夫条件不成立。
9. 若{X
n,n=1,2,…)是相互独立的随机变量序列,对每个n,X
n的分布列为
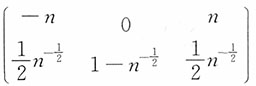
,问马尔可夫条件是否成立?
解:E(X
n)=0,

,而
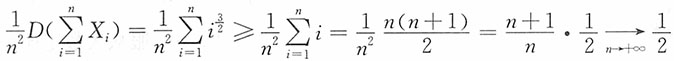
,故马尔可夫条件不成立。
10. 设在随机变量序列{X
n,n=1,2,…}中X
n仅与X
n-1及X
n+1相关,而与其他的随机变量都不相关,且对一切n,一致地有D(X
n)≤C(C为常数),则{X
n,n=1,2,…}服从大数定律。
证明:
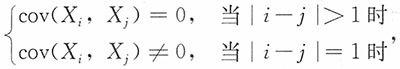
又
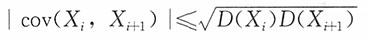
则
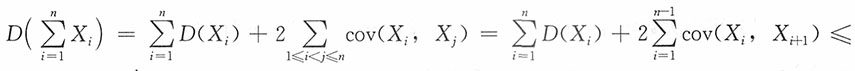

故
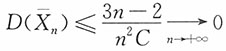
,{X
n,n=1,2,…}满足马尔可夫条件,即{X
n,n=1,2,…}服从大数定律。
11. 设{X
n,n=1,2,…}是相互独立的随机变量序列,且X
i,i=1,2,…的分布为
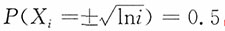
,则{Xn,n=1,2,…}不满足车贝雪夫大数定律的条件,但满足马尔可夫条件。
证明:注意到E(X
i)=0,
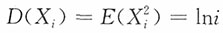
非一致有界,即{X
n,n=1,2,…}不满足车贝雪夫大数定律的条件。又
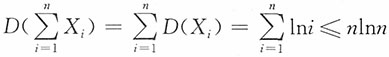
,则
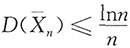
;又
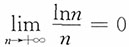
,则
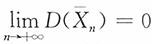
,即{X
n,n=1,2,…}满足马尔可夫条件。
12. 一加法器同时受到20个噪声电压V
k,k=1,2,…,20的影响,设它们是相互独立的随机变量,且都在区间(0,10)上服从均匀分布。记
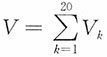
,求P(V105)的近似值。
解:E(V
k)=5,D(V
k)=100/12,k=1,2,…,20,
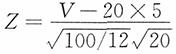
近似服从正态分布N(0,1),于是
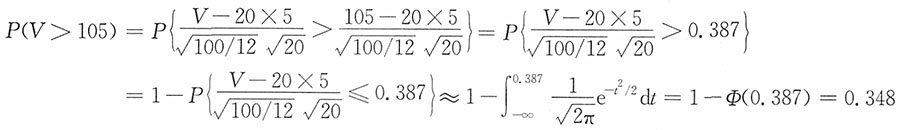
13. 一船舶在某海区航行,已知每遭受一次波浪的冲击,纵摇角大于3°的概率为p=1/3,若船舶遭受了90000次波浪冲击,问其中有29500~30500次纵摇角度大于3°的概率是多少?
解:将船舶每遭受一次波浪冲击看作是一次试验,并假定各次试验是独立的。将在90000次波浪冲击中纵摇角度大于3°的次数记为X,则X是一个随机变量,且有X~B(90000,1/3)。其分布列为
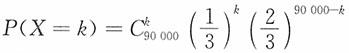
,k=1,2,…,90000,所求的概率为
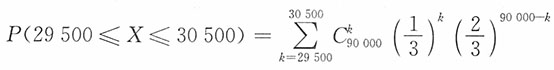
利用利莫弗-拉普拉斯定理来求它的近似值。即有
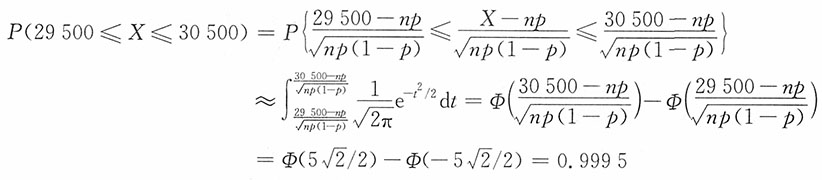
14. 求参加会议的家长人数X超过450的概率。
解:以X
k,k=1,2,…,400记第k个学生来参加会议的家长人数,则X
k的分布列为
P(X
k=0)=0.05,P(X
k=1)=0.8,P(X
k=2)=0.15
易知E(X
k)=1.1,D(X
k)=0.19,而
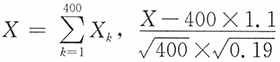
近似服从正态分布N(0,1),于是
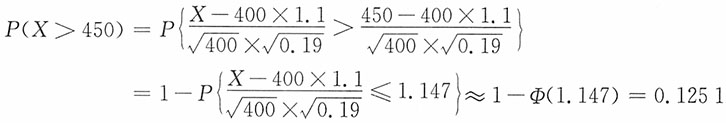
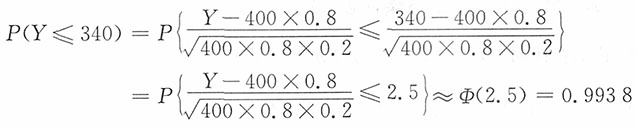
15. 求有1名家长来参加会议的学生人数不多余340的概率。
解:以Y记有1名家长参加会议的学生人数,则Y~B(400,0.8)。
16. 假设{X
i,i≥1}相互独立且都服从参数为λ的指数分布,记
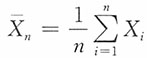
,则当n→∞时,
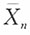
依概率收敛于
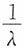
;
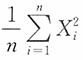
依概率收敛于

;
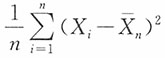
依概率收敛于
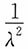
;
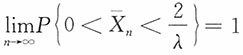
证明:X
1,X
2,…,X
n,…独立同分布,X
i~Exp(λ),
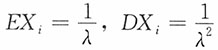

…独立同分布,
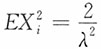
由辛钦大数定律知
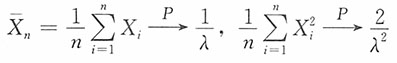
又
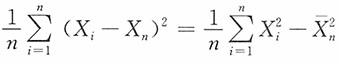
,则
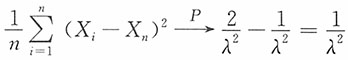
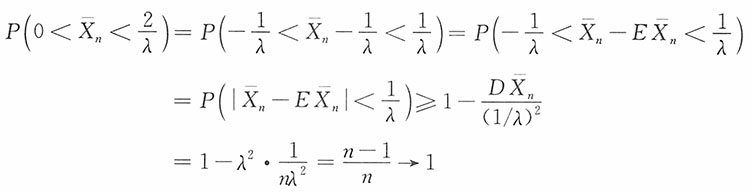
17. 一养鸡场购进1万只良种鸡蛋,已知每只鸡蛋孵化成雏鸡的概率为0.84,每只雏鸡育成种鸡的概率为0.9,试计算由这批鸡蛋得到种鸡不少于7500只的概率。
解:记事件A
k={第k只鸡蛋孵化成雏鸡},B
k={第k只鸡蛋育成种鸡}。
记

k=1,2,…,10000,则{X
k,k=1,2,…,10000}是相互独立且同分布的随机变量,且
P(X
k=1)=P(B
k)=P(A
k)P(B
k|A
k)=0.84×0.9=0.756
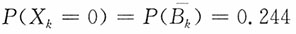
显然,
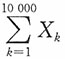
表示10000只鸡蛋育成的种鸡数,
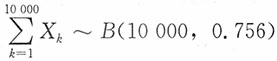
。所求概率为
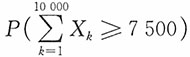
,根据棣莫弗—拉普拉斯中心极限定理可知
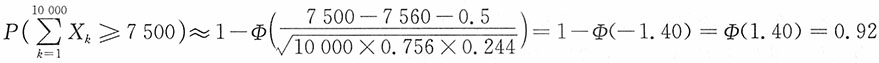
即由这批鸡蛋得到种鸡不少于7500只的概率为0.92。
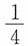
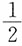
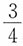
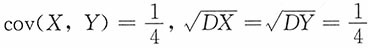
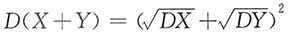
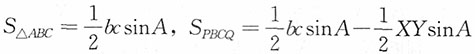 而X~U(0,c),Y~U(0,b)且相互独立,进而
而X~U(0,c),Y~U(0,b)且相互独立,进而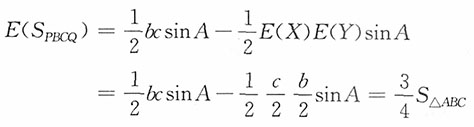
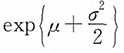
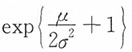
 ,Y=eX=eμeσZ,则
,Y=eX=eμeσZ,则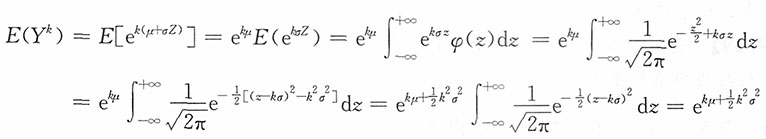
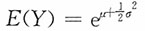
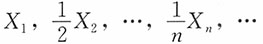
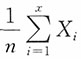 依概率收敛于数学期望,只要{Xn,n≥1)______。
依概率收敛于数学期望,只要{Xn,n≥1)______。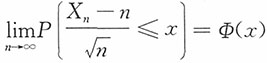
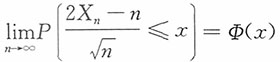
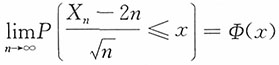
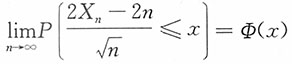
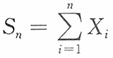 (n足够大),则Sn可用正态分布近似的充分条件是______。
(n足够大),则Sn可用正态分布近似的充分条件是______。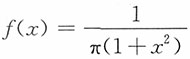
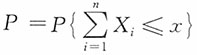 ,当”充分大时,有______。
,当”充分大时,有______。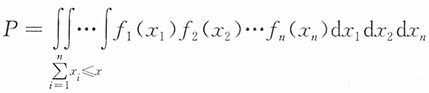 ,而题中并未明确Xi的期望与方差是否存在,故不能用中心极限定理计算,选A。
,而题中并未明确Xi的期望与方差是否存在,故不能用中心极限定理计算,选A。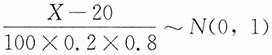 ,
,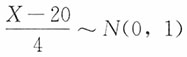 ,P(X=15)=P(15-0.5≤
,P(X=15)=P(15-0.5≤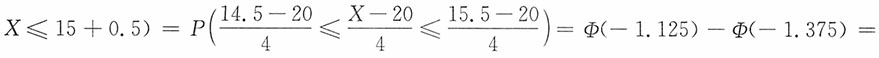
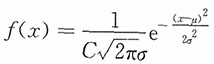 ,x≥0,C>0,σ>0,则称X服从截尾正态分布,记标准正态密度
,x≥0,C>0,σ>0,则称X服从截尾正态分布,记标准正态密度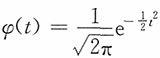 ,分布函数为Φ(t),请回答下列问题:
,分布函数为Φ(t),请回答下列问题: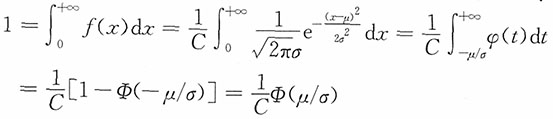
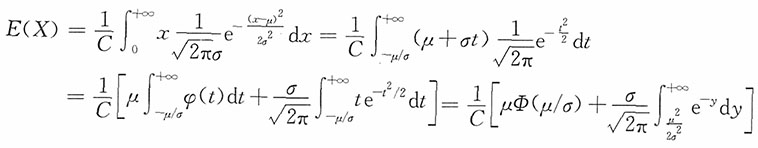
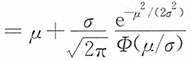
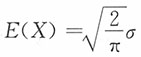
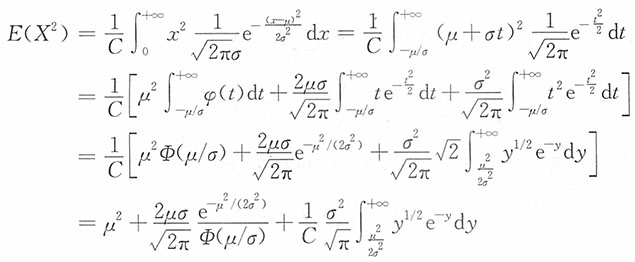
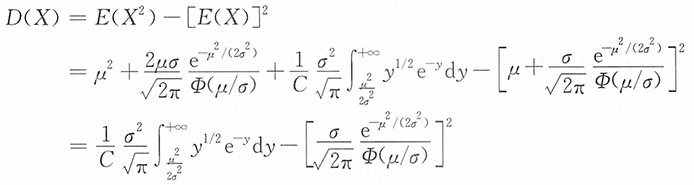
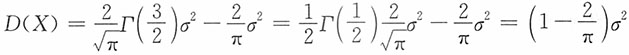 。
。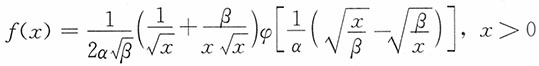
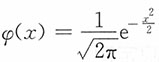 。
。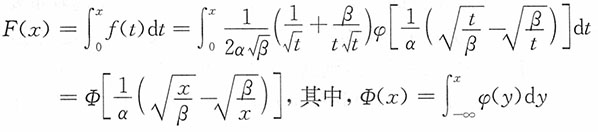
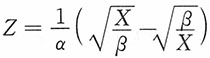 ,由(1)易见Z~N(0,1),又
,由(1)易见Z~N(0,1),又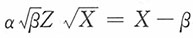 ,
,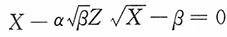 ,
,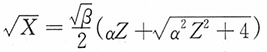

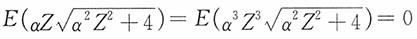
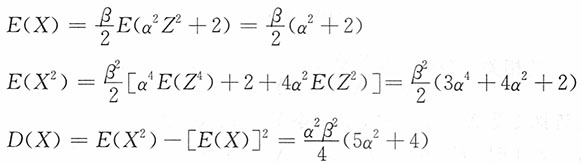
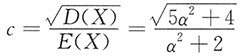
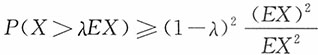 ,0<λ<1
,0<λ<1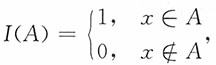 则
则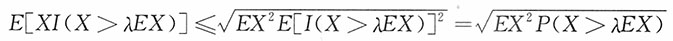
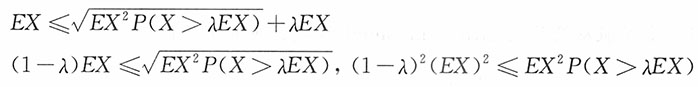
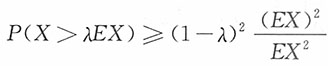
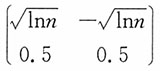 ,问{Xn,n=1,2,…}是否服从马尔科夫大数定律?
,问{Xn,n=1,2,…}是否服从马尔科夫大数定律?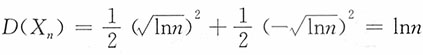 ,而
,而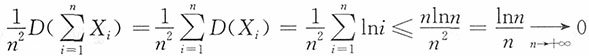 ,于是马尔可夫大数定律成立。
,于是马尔可夫大数定律成立。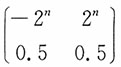 ,问马尔可夫条件是否成立?
,问马尔可夫条件是否成立?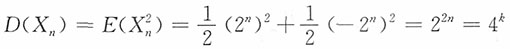 ,而
,而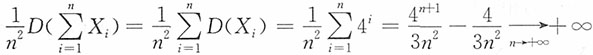 ,故马尔可夫条件不成立。
,故马尔可夫条件不成立。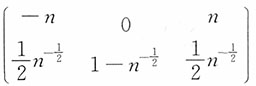 ,问马尔可夫条件是否成立?
,问马尔可夫条件是否成立? ,而
,而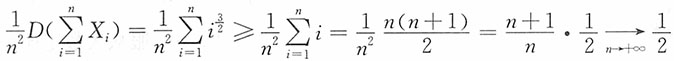 ,故马尔可夫条件不成立。
,故马尔可夫条件不成立。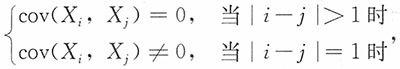 又
又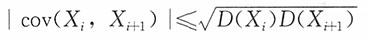
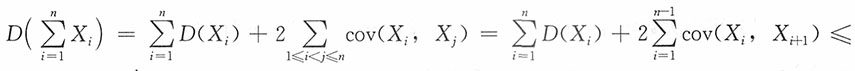

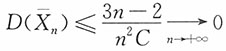 ,{Xn,n=1,2,…}满足马尔可夫条件,即{Xn,n=1,2,…}服从大数定律。
,{Xn,n=1,2,…}满足马尔可夫条件,即{Xn,n=1,2,…}服从大数定律。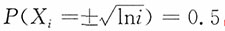 ,则{Xn,n=1,2,…}不满足车贝雪夫大数定律的条件,但满足马尔可夫条件。
,则{Xn,n=1,2,…}不满足车贝雪夫大数定律的条件,但满足马尔可夫条件。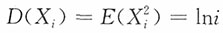 非一致有界,即{Xn,n=1,2,…}不满足车贝雪夫大数定律的条件。又
非一致有界,即{Xn,n=1,2,…}不满足车贝雪夫大数定律的条件。又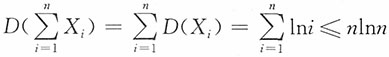 ,则
,则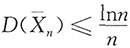 ;又
;又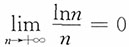 ,则
,则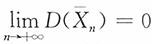 ,即{Xn,n=1,2,…}满足马尔可夫条件。
,即{Xn,n=1,2,…}满足马尔可夫条件。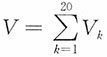 ,求P(V105)的近似值。
,求P(V105)的近似值。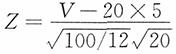 近似服从正态分布N(0,1),于是
近似服从正态分布N(0,1),于是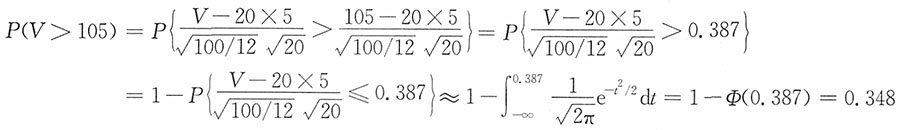
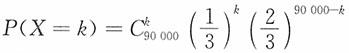 ,k=1,2,…,90000,所求的概率为
,k=1,2,…,90000,所求的概率为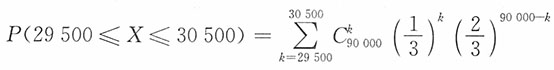
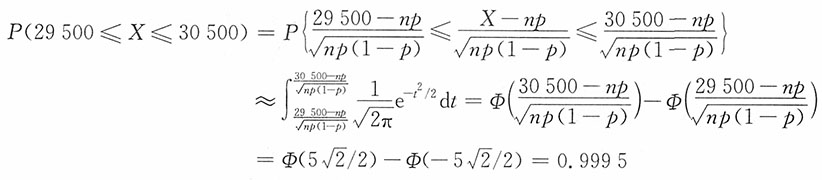
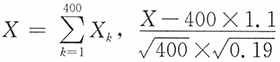 近似服从正态分布N(0,1),于是
近似服从正态分布N(0,1),于是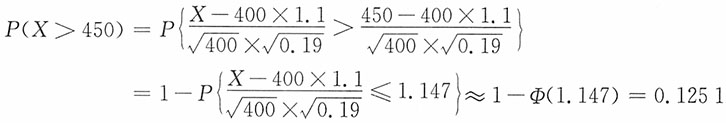

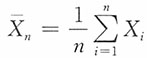 ,则当n→∞时,
,则当n→∞时,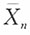 依概率收敛于
依概率收敛于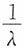 ;
;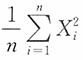 依概率收敛于
依概率收敛于 ;
;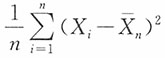 依概率收敛于
依概率收敛于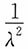 ;
;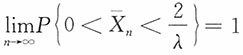
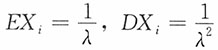
 …独立同分布,
…独立同分布,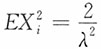
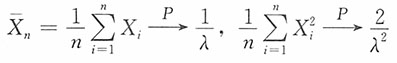
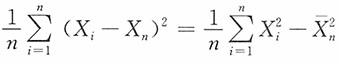 ,则
,则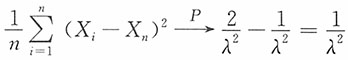
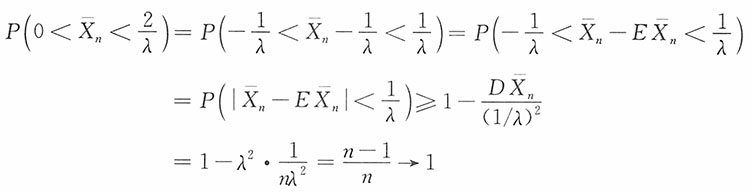
 k=1,2,…,10000,则{Xk,k=1,2,…,10000}是相互独立且同分布的随机变量,且
k=1,2,…,10000,则{Xk,k=1,2,…,10000}是相互独立且同分布的随机变量,且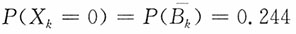
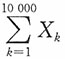 表示10000只鸡蛋育成的种鸡数,
表示10000只鸡蛋育成的种鸡数,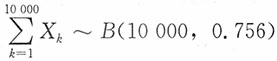 。所求概率为
。所求概率为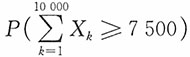 ,根据棣莫弗—拉普拉斯中心极限定理可知
,根据棣莫弗—拉普拉斯中心极限定理可知