单项选择题1. 设X
1,X
2,X
3,X
4是总体N(μ,σ
2)的样本,μ,σ未知,则统计量是______。
A.X
1+5X
4 B.
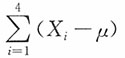
C.X
1-σ
D.
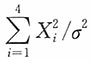
A B C D
2. 设总体
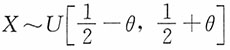
,其中θ为未知参数;又设X
1,X
2,…,X
n为来自总体X的一个样本,令
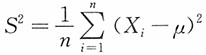
,则当μ为______时,S
2不是统计量。
A.
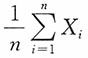
B.DX
C.
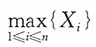
D.EX
A B C D
6. 设X
1,X
2,…,X
n来自总体N(μ,σ
2),且相互独立,则随机变量
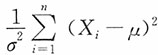
服从的分布是______。
A.χ
2(n-1)
B.
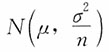
C.N(μ,σ
2)
D.χ
2(n)
A B C D
7. 设总体X~χ
2(n),X
1,X
2,…,X
n是样本,X是样本均值,则______。
A.
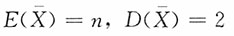
B.
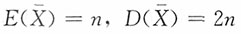
C.
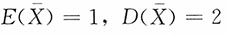
D.
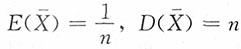
A B C D
10. 设X
1,X
2,…,X
n是取自N(0,1)的样本,且n≥2,
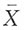
为样本均值,
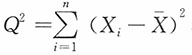
,则下列结论正确的是______。
A.
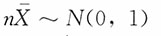
B.
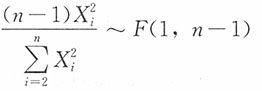
C.Q2~χ2(n)
D.
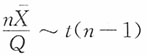
A B C D
17. 设X
1,X
2,…,X
n,n>1是来自总体期望为μ,总体方差为σ
2的样本,X样本均值,则______。
A.
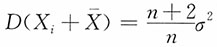
B.
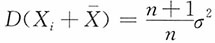
C.
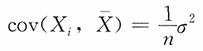
D.
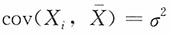
A B C D
21. 不重复抽样的抽样标准误公式比重复抽样多了一个系数______。
A.
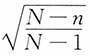
B.

C.
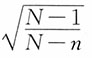
D.
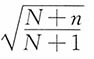
A B C D
A
[解析] 在重复抽样时,样本均值的抽样标准误为
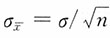
,在不重复抽样时,样本均值的标准误为
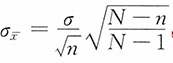
,其中
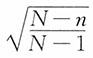
为修正系数。对于无限总体进行不重复抽样时,可以按照重复抽样计算。当总体为有限总体,N比较大而n/N≥5%时,修正系数可以简化为
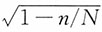
;当N比较大而n/N<5%时,修正系数可以近似为1,即可以按重复抽样计算。
计算题设总体X~N(0,1),X1,X2为其一个简单随机样本,求1.
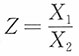
的密度函数。
解:(X
1,X
2)的联合密度为f
(X1,X2)(x
1,x
2)=φ(x
1)φ(x
2),对-∞<z<+∞,
有
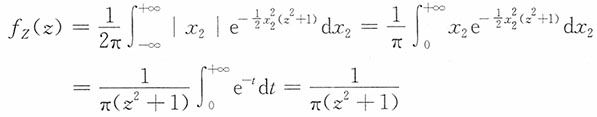
即Z服从标准柯西分布。
2.
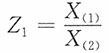
的密度函数。
解:(X(1),X(2))的联合密度函数为f
(X(1),X(2))(x
1,x
2)=2φ(x
1)φ(x
2),x
1≤x
2。
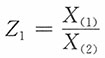
的密度函数为
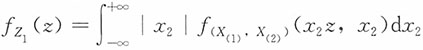
。
注意到x
1≤x
2,即x
2z≤x
2,(z-1)x
2≤0,也即,当z<1时,x
2>0;当x≥1时,x
2≥0。
当z<1时,
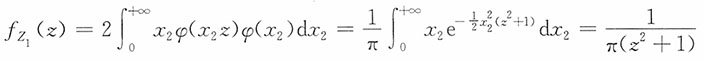
当z>1时,
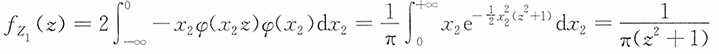
即Z
1服从标准柯西分布。
3.
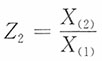
的密度函数。
解:同理知,Z
2服从标准柯西分布。也即
(X(1),X(2))的联合密度为f
(X(1),X(2))(x
1,x
2)=2φ(x
1)φ(x
2),x
1≤x
2 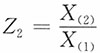
的密度函数为
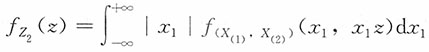
注意到x
1≤x
2,即x
1≤x
1z,(z-1)x
1≥0,也即,当z<1时,x
1<0;当z≥1时,x
1≥0。
当z>1时,
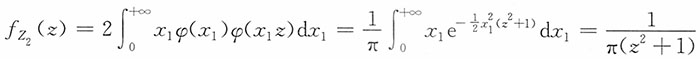
当z<1时,
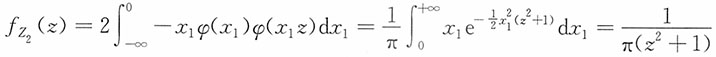
或者利用结论:若Z~t(1),则有
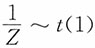
。
F(x)=1-e-λx,f(x)=λe-λx,x>0,λ>0
设X1,X2,…,Xn为总体X的一个简单随机样本,X(1)≤X(2)≤…≤X(n)为其次序统计量,求4. X
(k),k=1,2,…,n的密度函数,E(X
(k)),D(X
(k))。
解:对y>0,
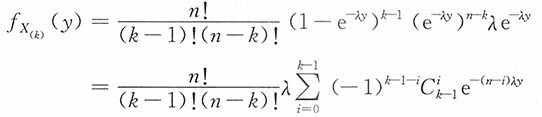
记Y
i=λX
i,i=1,2,…,n,则Y
1,Y
2,…,Y
n独立且同服从标准指数分布Exp(1)

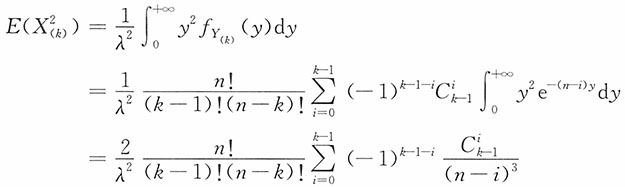
进而有
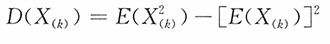
[解析] (1)X
(1)的密度函数为f
X(1)(y)=n[1-F(y)]
n-1-f(y)=nλe
-nλy,y>0。易见X
(1)仍服从指数分布,此时参数为nλ,即
(1)~Exp(nλ)。
(2)X
(n)的密度函数为f
X(n)(y)=n[F(y)]
n-1f(y)=nλe
-λy[1-e-λy]
n-1,y>0,而X
(n)并不服从指数分布。
(3)一般地,对j=1,2,…,X
(k)的j阶矩
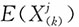
为
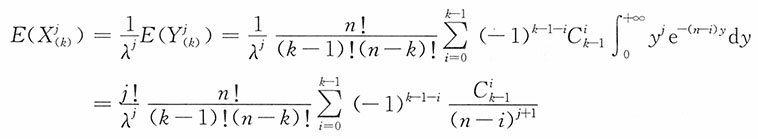
(4)如果用随机变量X表示某种产品的寿命,从中抽取n个产品做寿命试验,试验做到有r个产品失效为止(被称为定数截尾寿命试验),此时次序失效时间为X
(1),X
(2),…,X
(r),统计量
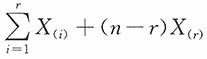
实质上是产品总的试验时间。
5. 极差
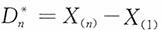
的密度函数。
解:对y>0,
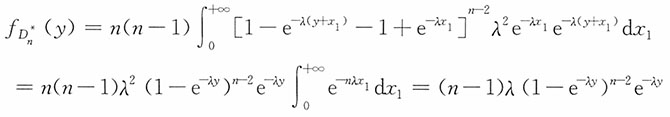
6. 对1≤r≤n,X
(1),X
(2),…,X
(r)的联合密度函数。
解:对0≤y
1<y
2<…<y
r,
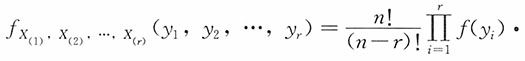
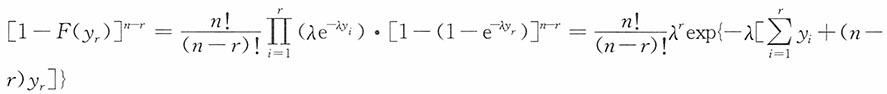
7. 设总体X~U[0,θ],θ>0为未知参数,X
1,X
2,…,X
n是来自总体X的一个简单随机样本,求θ的一个充分统计量。
解:设样本观测值为x
1,x
2,…,x
n,样本X
1,X
2,…,X
n的联合密度函数为
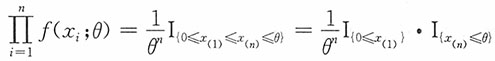
取t=x
(n),
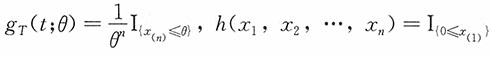
,则X
(n)为θ的充分统计量。
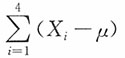
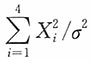
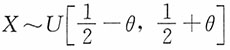 ,其中θ为未知参数;又设X1,X2,…,Xn为来自总体X的一个样本,令
,其中θ为未知参数;又设X1,X2,…,Xn为来自总体X的一个样本,令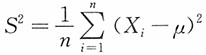 ,则当μ为______时,S2不是统计量。
,则当μ为______时,S2不是统计量。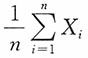
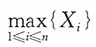
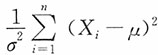 服从的分布是______。
服从的分布是______。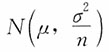
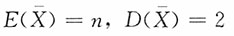
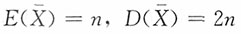
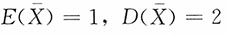
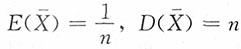
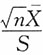
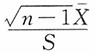
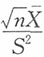
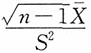
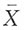 为样本均值,
为样本均值,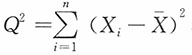 ,则下列结论正确的是______。
,则下列结论正确的是______。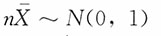
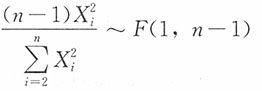
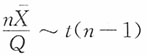
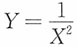 ,则______。
,则______。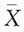 近似服从______的正态分布。
近似服从______的正态分布。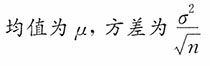
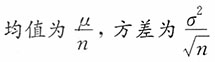
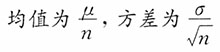
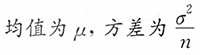
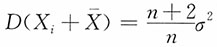
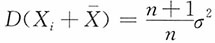
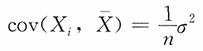
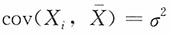
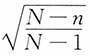

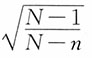
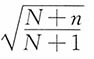
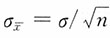 ,在不重复抽样时,样本均值的标准误为
,在不重复抽样时,样本均值的标准误为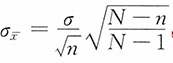 ,其中
,其中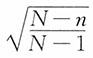 为修正系数。对于无限总体进行不重复抽样时,可以按照重复抽样计算。当总体为有限总体,N比较大而n/N≥5%时,修正系数可以简化为
为修正系数。对于无限总体进行不重复抽样时,可以按照重复抽样计算。当总体为有限总体,N比较大而n/N≥5%时,修正系数可以简化为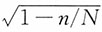 ;当N比较大而n/N<5%时,修正系数可以近似为1,即可以按重复抽样计算。
;当N比较大而n/N<5%时,修正系数可以近似为1,即可以按重复抽样计算。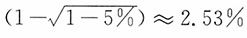 ,也即
,也即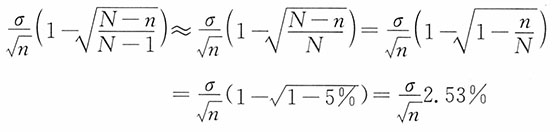

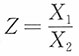 的密度函数。
的密度函数。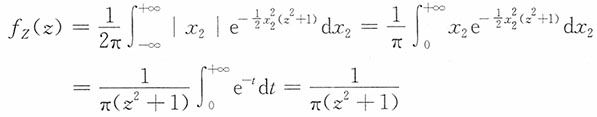
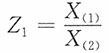 的密度函数。
的密度函数。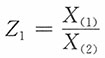 的密度函数为
的密度函数为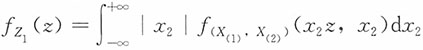 。
。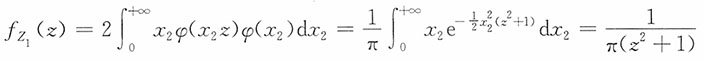
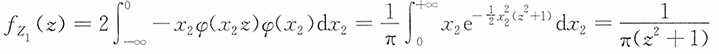
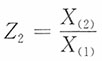 的密度函数。
的密度函数。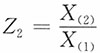 的密度函数为
的密度函数为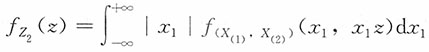
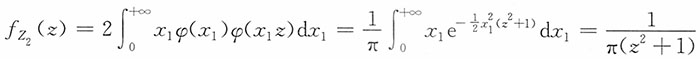
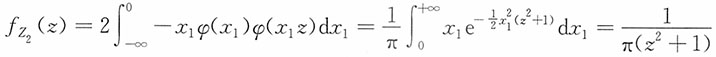
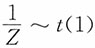 。
。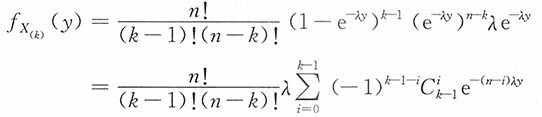

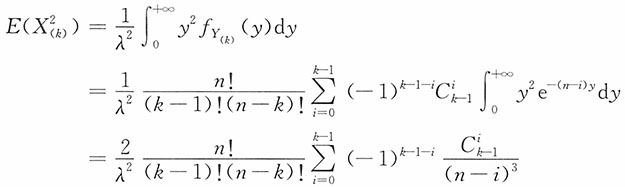
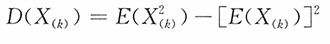
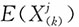 为
为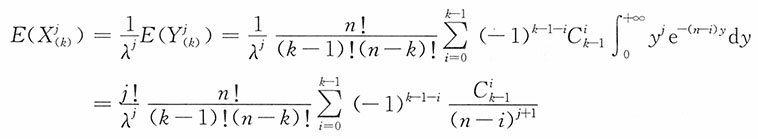
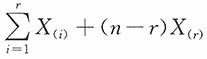 实质上是产品总的试验时间。
实质上是产品总的试验时间。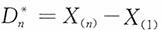 的密度函数。
的密度函数。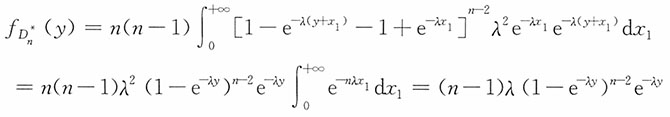
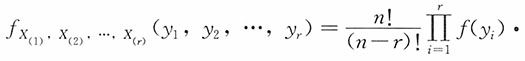
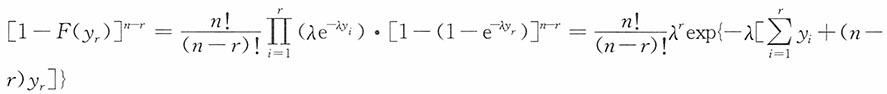
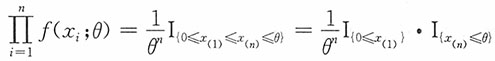
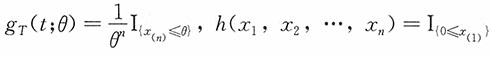 ,则X(n)为θ的充分统计量。
,则X(n)为θ的充分统计量。