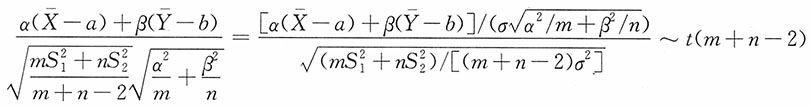计算题1. 为研究吸烟与慢性气管炎的关系,随机地抽查了205名50岁以上吸烟的人,其中有43人患有慢性气管炎,请计算有95%的把握可以认为有慢性气管炎的人数比例不低于多少。(保留四位)(z
0.025=1.96,z
0.05=1.645,Φ(1.96)=0.975,Φ(1.645)=0.95)
解:
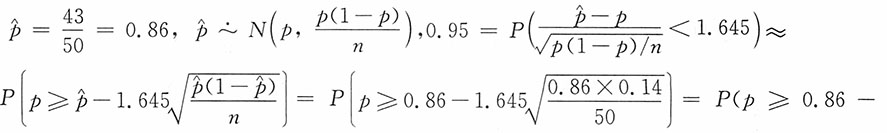
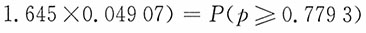
,即比例不低于0.7793。
2. 设总体X
i,i=1,2服从正态分布
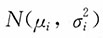
,X
1和X
2相互独立;由来自总体X
i,i=1,2的简单随机样本,得样本均值
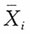
和样本方差
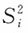
。(1)证明:4个随机变量
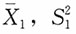
,
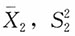
相互独立。(2)假设μ
1=μ
2=μ,证明:
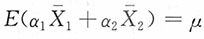
,其中,α
i是统计量:
解:设X
11,X
12,…,X
1n为来自
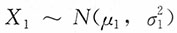
的一个简单随机样本,X
21,X
22,…,X
2m为来自
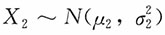
的一个简单随机样本。
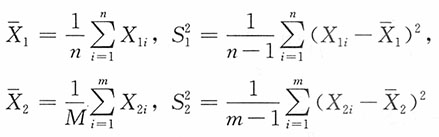
(1)对-∞<s,u<+∞,t,v>0,
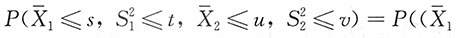
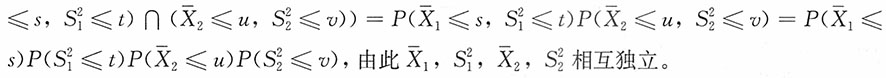
(2)易见α
1与
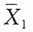
独立,α
2与
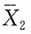
独立。
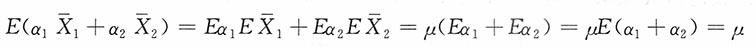
3. 设F(x)是总体X的分布函数,F
n(x)是基于来自总体X的容量为n的简单随机样本的经验分布函数。对于任意给定的x,-∞<x<+∞,试求F
n(x)的概率分布、数学期望和方差。
解:设n
x表示在总体X的n次抽样事件(X≤x)出现的次数,则n
x~B(n,F(x))经验分布函数
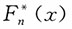
可以表示为
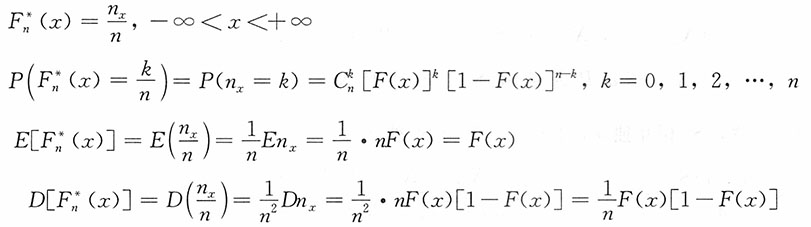
4. 已知(X,Y)的概率密度为
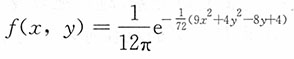
求证明:
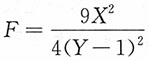
服从参数为(1,1)的F分布。
证明:
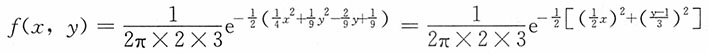
则(X,Y)服从二元正态分布,且X~N(0,2
2),Y~N(1,3
2),X,Y独立。
则
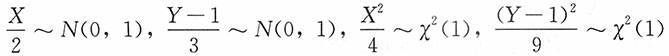
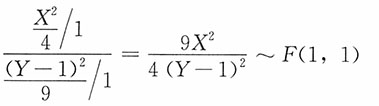
5. 设总体X服从标准正态分布N(0,1),X
1,X
2,…,X
2n是来自总体为X,容量为2n的简单随机样本,求下列统计量的分布。
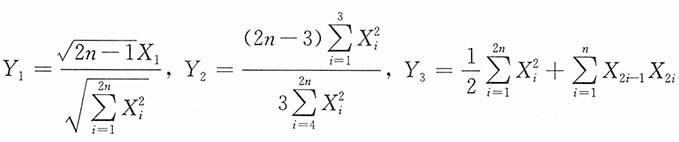
解:X
i~N(0,1),i=1,2,…,2n,由于X
1~N(0,1),

,则
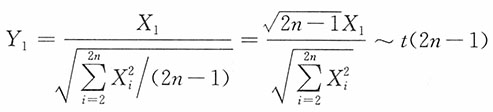
由于
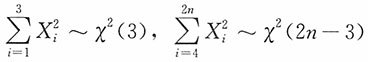
,则
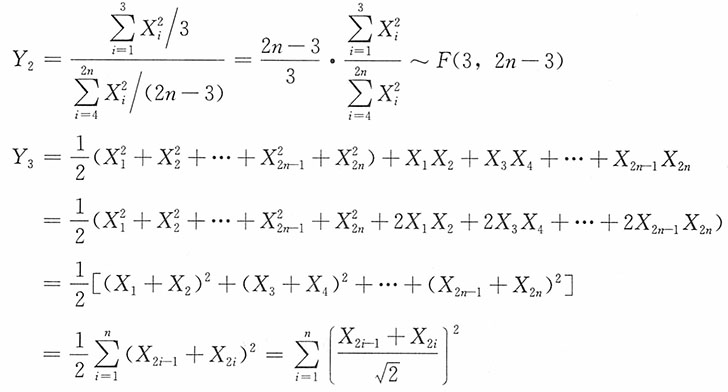
由于E(X
2i-1+X
2i)=0,D(X
2i-1+X
2i)=2

则Y
3~χ
2(n)
6. 设总体X服从具有E(X)=0,
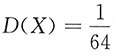
的正态分布,X
1,X
2,X
3为总体X的一个简单随机样本。记Y
1=(X
1-X
2)
2,

,试问Y
1,Y
2,Y
3各统计量分别服从什么分布?
解:令σ=1/8,则X~N(0,σ
2)
而X
1-X
2~N(0,2σ
2),
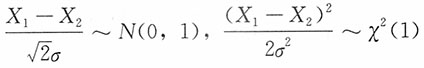
于是
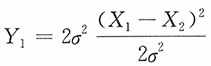
的密度函数为
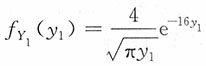
,y
1>0
又
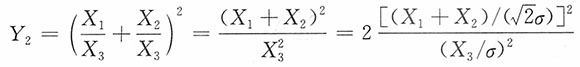
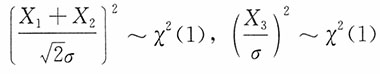
,且两者独立,则有
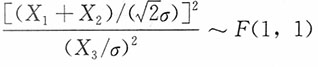
进而Y
2的密度函数为
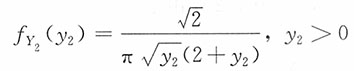
又
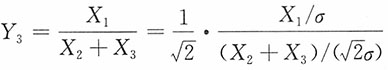
,由于
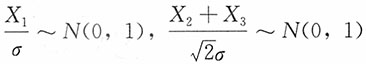
,且两者独立,则有
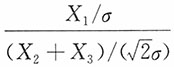
服从柯西分布。
进而Y
3的密度函数为
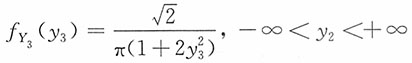
7. 设X
1,X
2是来自正态总体N(μ,σ
2)的一个简单随机样本,则(X
1+X
2)
2与(X
1-X
2)
2相互独立。
证明:方法一:由于
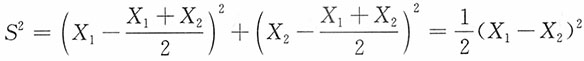
,则有费歇定理知X
1+X
2与(X
1-X
2)
2独立,进而(X
1+X
2)
2与(X
1-Y
2)
2也独立。
方法二:X
1+X
2~N(2μ,2σ
2),X
1-X
2~N(0,2σ
2),
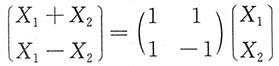
且矩阵
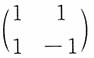
可逆,则
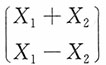
服从二维正态分布。而
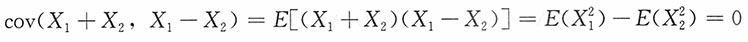
故X
1+X
2,X
1-X
2不相关,进而也独立,于是有(X
1+X
2)
2与(X
1-X
2)
2相互独立。
方法三:X
1,X
2的联合密度为
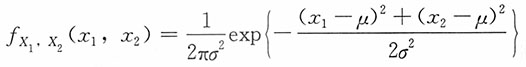
令
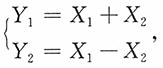
则
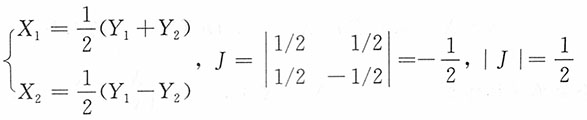
由此,Y
1,Y
2的联合密度为

即得Y
1~N(2μ,2σ
2),Y
2~N(0,2σ
2),且Y
1,Y
2相互独立,进而(X
1+X
2)
2与(X
1-X
2)
2也相互独立。
8. 若总体X~N(μ,1),X
1,X
2,…,X
n为X的一个样本,证明
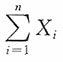
为充分统计量。
9. 当n很大时(通常n>45)则
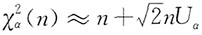
。
证明:利用中心极限定理求其近似值,即
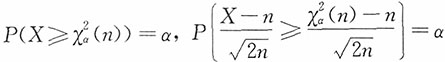
由于
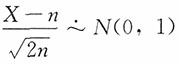
,则有
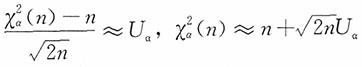
。
10. 设X
1,X
2,…,X
n独立同分布N(μ,σ
2),令
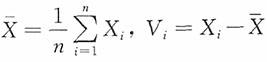
,i=1,2,…,n,问
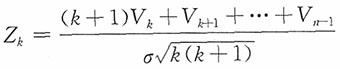
服从什么分布,k=1,2,…,n-1。
解:
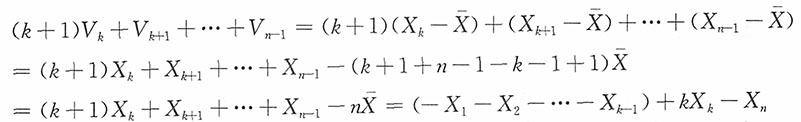
于是Z
k是独立正态分布随机变量X
1,X
2,…,X
k,X
n的线性组合,所以Z
k服从正态分布。
而
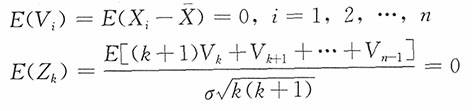
D[(k+1)V
k+V
k+1+…+V
n-1]=D[(-X
1-X
2-…-X
k-1)+kX
k-X
n]
=D(X
1)+…+D(X
k-1)+k
2D(X
k)+D(X
n)
=[(k-1)+k
2+1]σ
2=(k
2+k)σ
2 由此(k+1)V
k+V
k+1+…+V
n-1~N(0,(k
2+k)σ
2),标准化后即Z
k~N(0,1)。
11. 已知X
1,X
2,X
3独立且服从N(0,σ
2)分布,证明
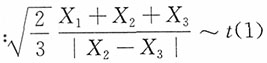
。
证明:记Y
1=X
2+X
3,Y
2=X
2-X
3,则E(Y
1)=E(Y
2)=0,D(Y
1)=D(Y
2)=2σ
2。
由于X
2,X
3独立且同服从N(0,σ
2),则Y
1~N(0,2σ
2),Y
2~N(0,2σ
2)。
又
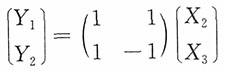
,且矩阵
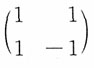
可逆,则(Y
1,Y
2)服从二维正态分布。再者,又
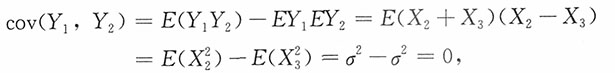
故Y
1,Y
2独立且同服从N(0,2σ
2)分布并与X,独立。
对任意的x
1,y
1,y
2,P(X
1≤x
1,Y
1≤y
1,Y
2≤y
2)=P(X
1≤x
1,(Y
1≤y
1,Y
2≤y
2))
=P(X
1≤x
1)P(Y
1≤y
1,Y
2≤y
2)=P(X
1≤x
1)P(Y
1≤y
1)P(Y
2≤y
2)
即有X
1,Y
1,Y
2相互独立,进而X
1+X
2+X
3与X
2-X
3也相互独立。
又
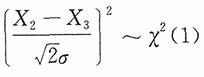
,则
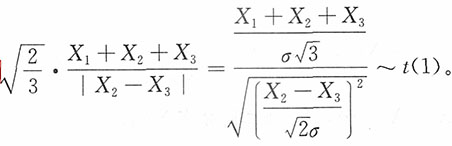
。
12. 设(X
1,X
2)是取自正态总体X~N(0,σ
2)的一个样本,求
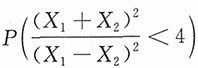
。
解:由于X
1+X
2~N(0,2σ
2),X
1-X
2~N(0,2σ
2),
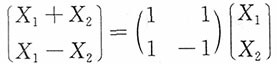
,且矩阵
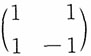
可逆,则
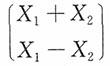
服从二维正态分布。而
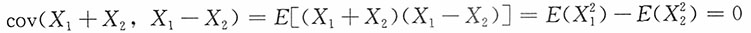
故X
1+X
2,X
1-X
2不相关,进而也独立,于是有(X
1+X
2)
2,(X
1-X
2)
2相互独立。又
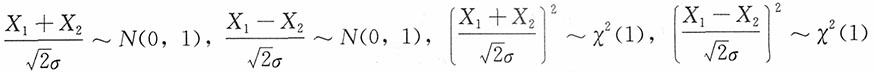
由此
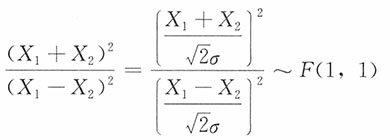
记
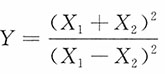
的密度函数为f
Y(y),
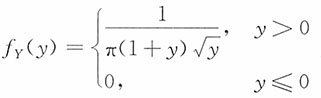
所以
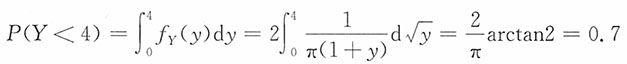
13. 设总体X的均值μ与方差σ
2存在,X
1,X
2,…,X
n为总体X的一个简单随机样本,试证明:对i≠j,
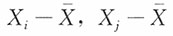
的相关系数:
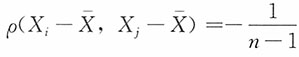
。
证明:对i=1,2,…,n,有
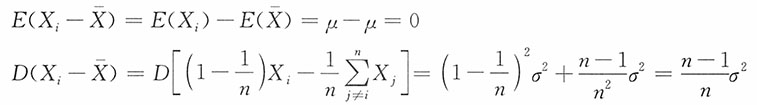
对i≠j,
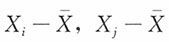
的协方差为
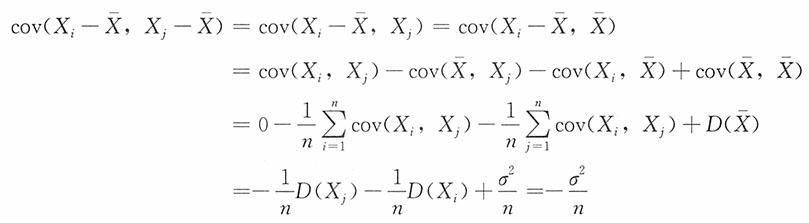
对i≠j,
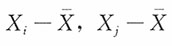
的相关系数为
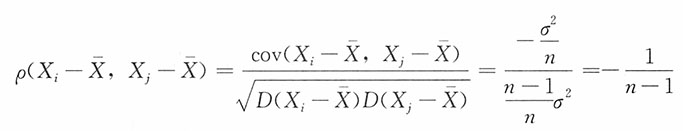
14. 设总体X的分布函数F(x)严格单调增加,X
1,X
2,…,X
n是来自总体X的一个简单随机样本,则有
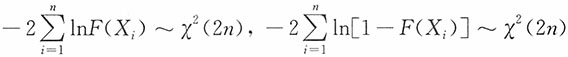
。
证明:由于分布函数F(x)严格单调增加,则F(X)~U[0,1],1-F(X)~U[0,1],
进而有-lnF(X)~Exp(1),-ln[1-F(X)]~Exp(1),
-2lnF(X)~χ2(2),-2ln[1-F(X)]~χ2(2)
由于X1,X2,…,Xn相互独立且同分布,则-2lnF(X1),-2lnF(X2),…,-2lnF(Xn)相互独立且同服从χ2(2);-2ln[1-F(X1)],-2ln[1-F(X2)],…,-2ln[1-F(Xn)]也相互独立且同服从χ2(2)。由χ2分布的可加性知
15. 设总体X~N(0,1),X
1,X
2,X
3为其一个简单随机样本,试证明:
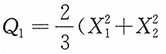
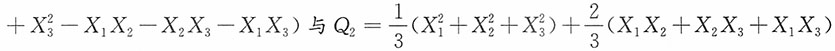
相互独立,且分别服从χ
2(2)与χ
2(1)。
证明:由于
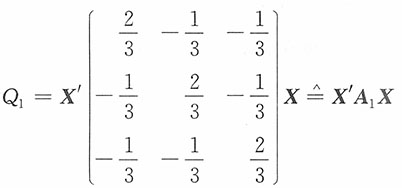
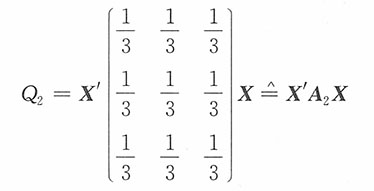
其中,X'=(X
1,X
2,X
3)。又
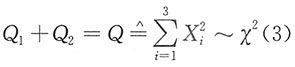
,n=3,而A
1,A
2的秩分别为n
1=2,n
2=1,即n
1+n
2=3=n。由柯赫伦定理:Q
1~χ
2(2),Q
2~χ
2(1),且相互独立。
16. 设X
1,X
2,X
3,X
4相互独立同服从N(0,1),令Y=X
1X
2+X
3X
4,则Y的密度函数为
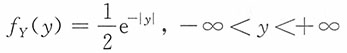
证明:注意到
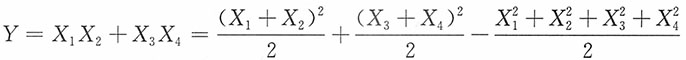
作如下线性变换:
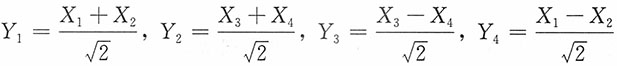
则(Y
1,Y
2,Y
3,Y
4)'=A(X
1,X
2,X
3,X
4)',其中
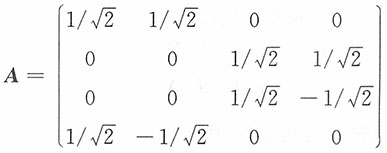
则
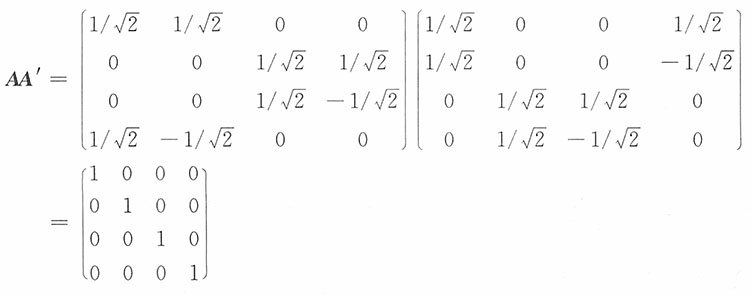
即矩阵A是正交阵,也即上述线性变换为正交变换。
则
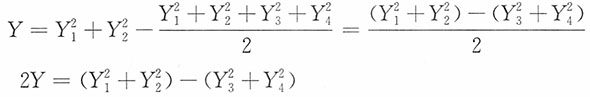
由于X
1,X
2,X
3,X
4相互独立同服从N(0,1),经过正交变换后得到的Y
1,Y
2,Y
3,Y
4也是独立且同服从N(0,1),于是
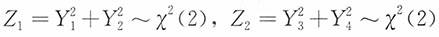
,且两者独立。
又

下面求
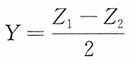
的分布函数
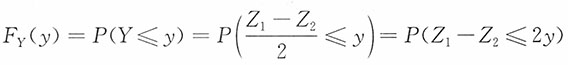
当y<0,

当y≥0,
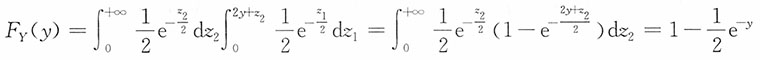
进而得Y的密度函数为
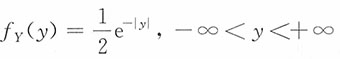
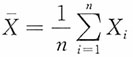 ,
, 。
。17. 证明:E(T)=μ
2。
解:由费歇定理知:
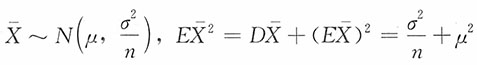
,又ES
2=σ
2由此
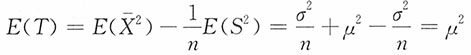
18. 当μ=0,σ=1时,求D(T)。
解:当μ=0,σ=1时,即X
1,X
2,…,X
n是总体X~N(0,1)的一个简单随机样本。由费歇定理知:
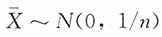
,(n-1)S
2~χ
2(n-1),
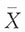
与S
2独立,进而
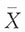
与S
2独立。注意到
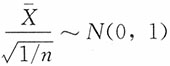
,进而
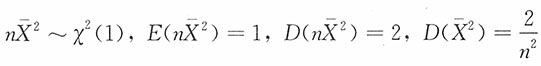
,又注意到
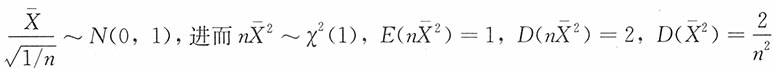
,又
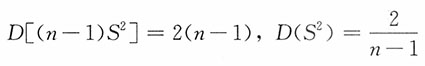
因此,
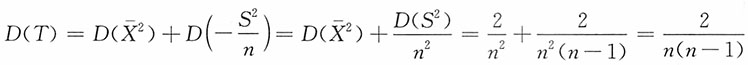
19. 设(X
i,X
j),i=1,2,…,n是来自二维正态分布
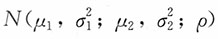
的一个简单随机样本,记
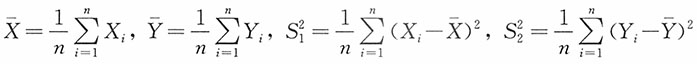
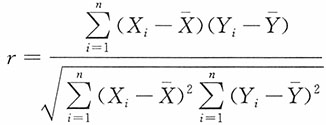
,求统计量
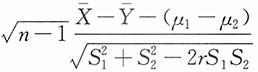
的分布。
解:注意到

令Z
i=X
i-Y
i,
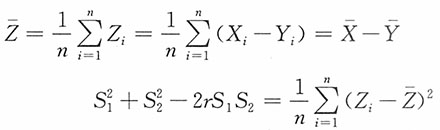
由此
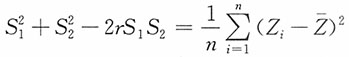
又
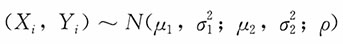
,i=1,2,…,n,则X
i-Y
i也服从正态分布。
而
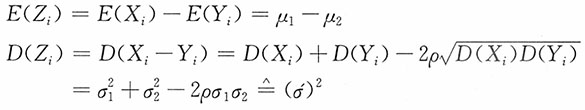
即Z
i~N(μ
1-μ
2,(σ')
2),由此
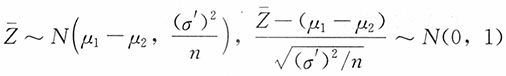
。
又
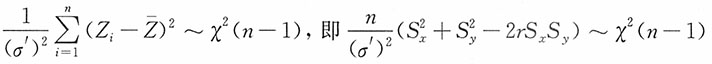
则
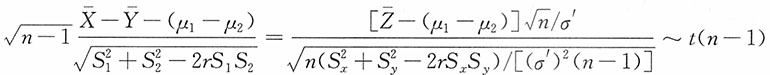
20. 设X
1X
2,…,X
m;Y
1,Y
2,…,Y
n独立。X
i~N(a,σ
2),i=1,2,…,m,Y
i~N(b,σ
2),i=1,2,…,n,
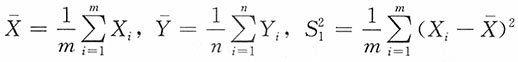
,
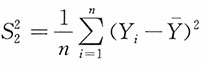
,而α,β为常数。试求
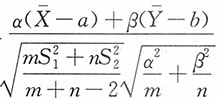
的分布。
解:由于X
i~N(a,σ
2),i=1,2,…,m,Y
i~N(b,σ
2),i=1,2,…,n;且X
1,X
2,…,X
m,Y
1,Y
2,…,Y
n相互独立,则
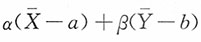
也服从正态分布。
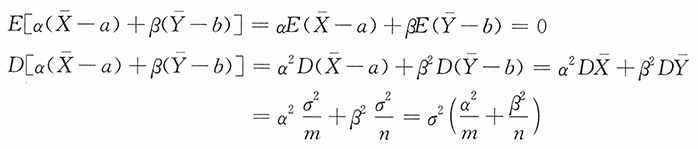
所以
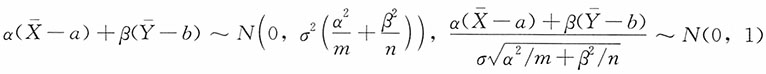
,而又

,且
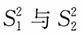
独立,则
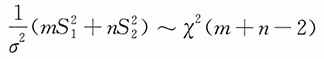
对-∞<t
1,t
2<+∞,s
1,s
2>0,则有
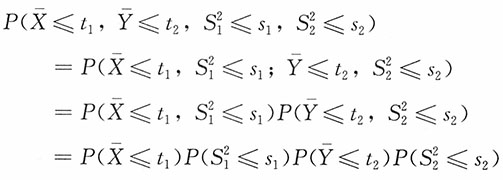
则
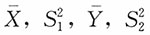
相互独立,进而
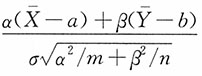
与
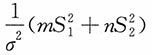
独立,则
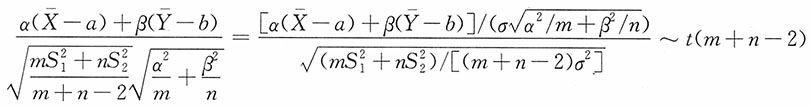
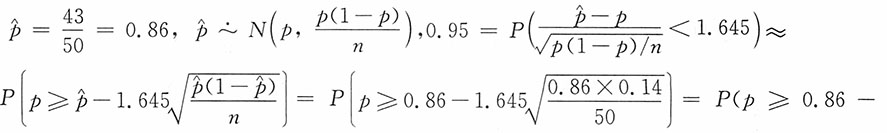
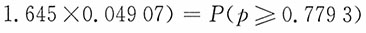 ,即比例不低于0.7793。
,即比例不低于0.7793。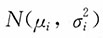 ,X1和X2相互独立;由来自总体Xi,i=1,2的简单随机样本,得样本均值
,X1和X2相互独立;由来自总体Xi,i=1,2的简单随机样本,得样本均值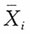 和样本方差
和样本方差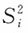 。(1)证明:4个随机变量
。(1)证明:4个随机变量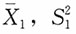 ,
,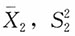 相互独立。(2)假设μ1=μ2=μ,证明:
相互独立。(2)假设μ1=μ2=μ,证明: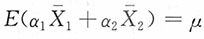 ,其中,αi是统计量:
,其中,αi是统计量: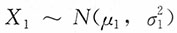 的一个简单随机样本,X21,X22,…,X2m为来自
的一个简单随机样本,X21,X22,…,X2m为来自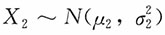 的一个简单随机样本。
的一个简单随机样本。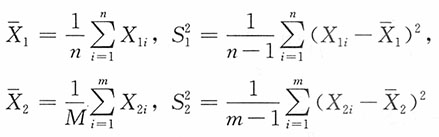
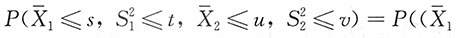
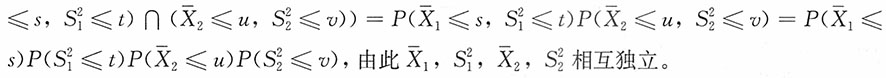
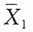 独立,α2与
独立,α2与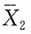 独立。
独立。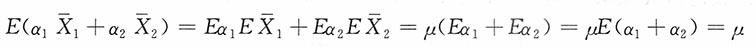
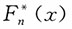 可以表示为
可以表示为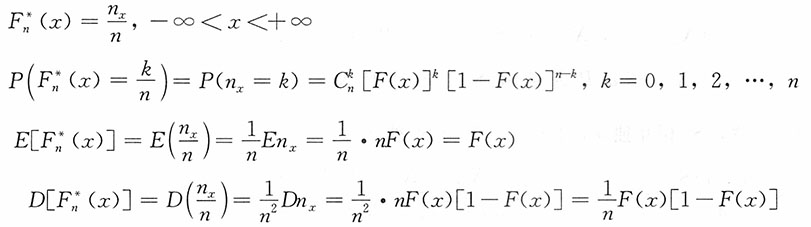
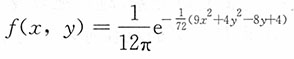 求证明:
求证明: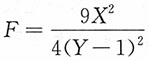 服从参数为(1,1)的F分布。
服从参数为(1,1)的F分布。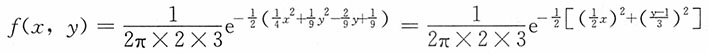
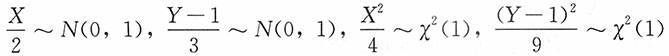
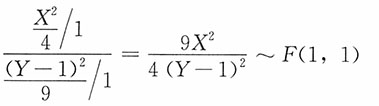
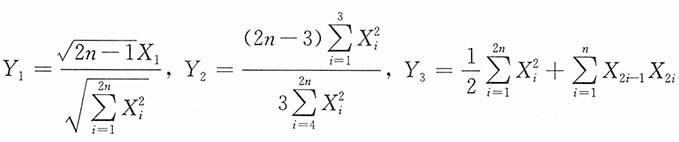
 ,则
,则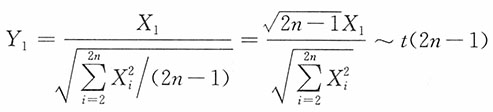
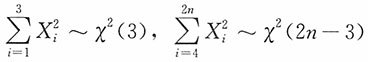 ,则
,则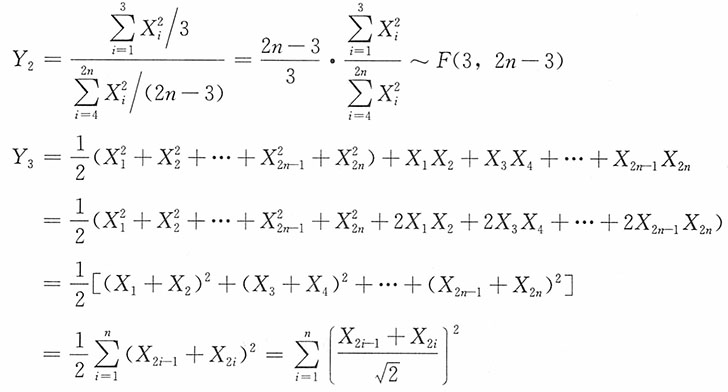

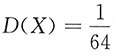 的正态分布,X1,X2,X3为总体X的一个简单随机样本。记Y1=(X1-X2)2,
的正态分布,X1,X2,X3为总体X的一个简单随机样本。记Y1=(X1-X2)2, ,试问Y1,Y2,Y3各统计量分别服从什么分布?
,试问Y1,Y2,Y3各统计量分别服从什么分布?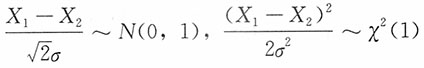
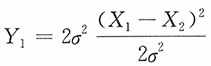 的密度函数为
的密度函数为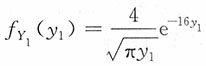 ,y1>0
,y1>0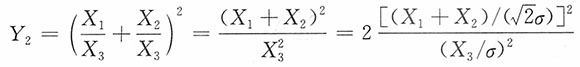
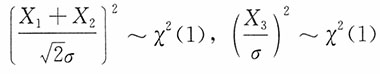 ,且两者独立,则有
,且两者独立,则有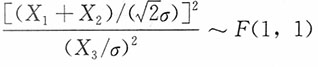
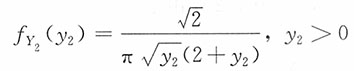
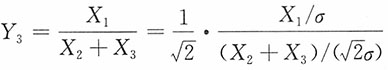 ,由于
,由于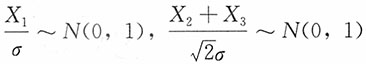 ,且两者独立,则有
,且两者独立,则有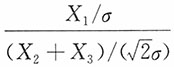 服从柯西分布。
服从柯西分布。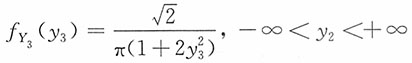
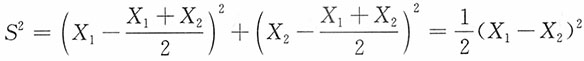 ,则有费歇定理知X1+X2与(X1-X2)2独立,进而(X1+X2)2与(X1-Y2)2也独立。
,则有费歇定理知X1+X2与(X1-X2)2独立,进而(X1+X2)2与(X1-Y2)2也独立。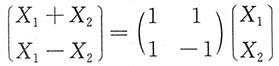
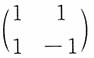 可逆,则
可逆,则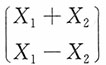 服从二维正态分布。而
服从二维正态分布。而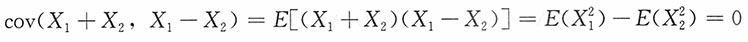
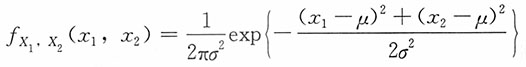
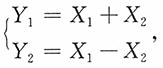 则
则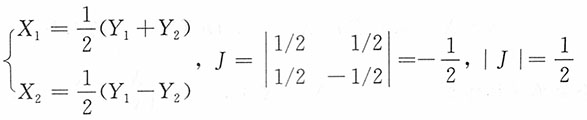

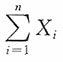 为充分统计量。
为充分统计量。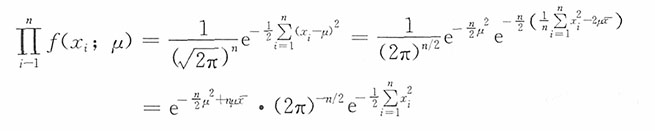
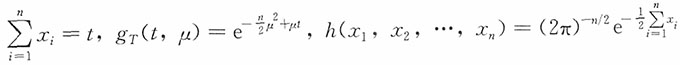 ,由因子分解定理知
,由因子分解定理知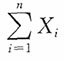 为充分统计量。
为充分统计量。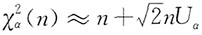 。
。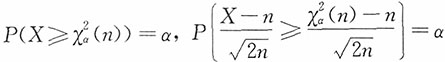
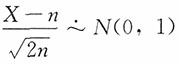 ,则有
,则有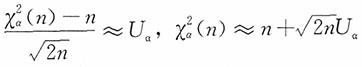 。
。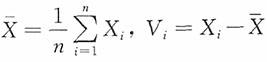 ,i=1,2,…,n,问
,i=1,2,…,n,问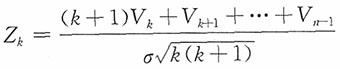 服从什么分布,k=1,2,…,n-1。
服从什么分布,k=1,2,…,n-1。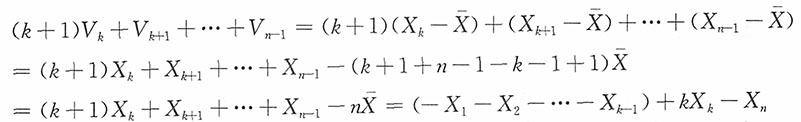
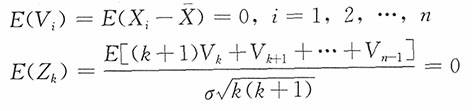
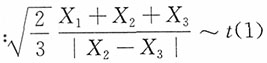 。
。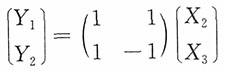 ,且矩阵
,且矩阵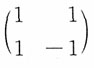 可逆,则(Y1,Y2)服从二维正态分布。再者,又
可逆,则(Y1,Y2)服从二维正态分布。再者,又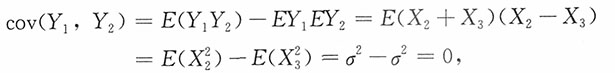
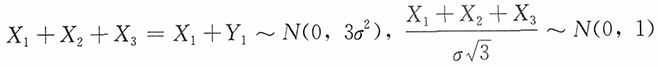
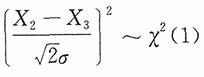 ,则
,则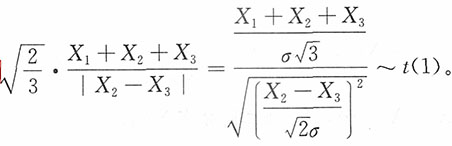 。
。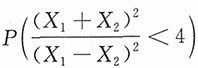 。
。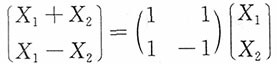 ,且矩阵
,且矩阵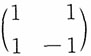 可逆,则
可逆,则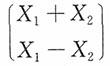 服从二维正态分布。而
服从二维正态分布。而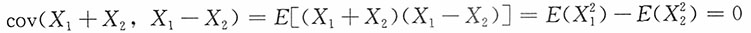
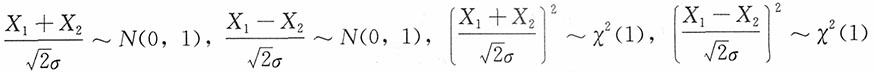
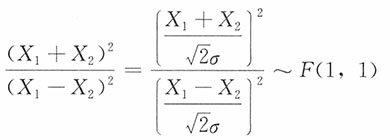
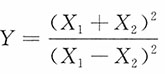 的密度函数为fY(y),
的密度函数为fY(y),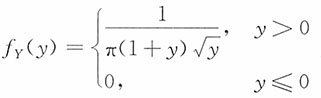
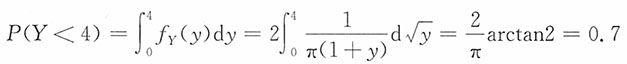
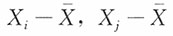 的相关系数:
的相关系数: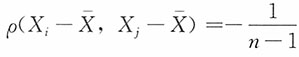 。
。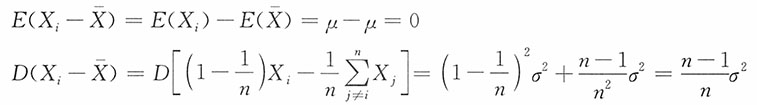
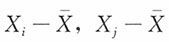 的协方差为
的协方差为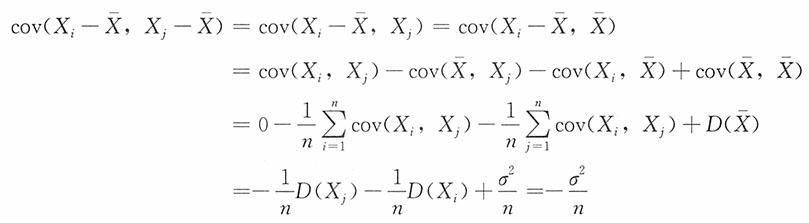
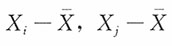 的相关系数为
的相关系数为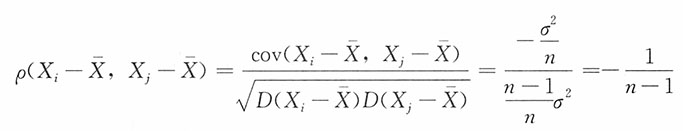
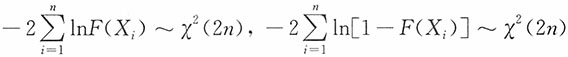 。
。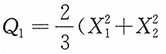
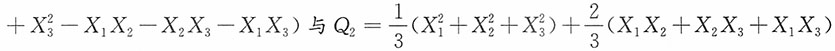 相互独立,且分别服从χ2(2)与χ2(1)。
相互独立,且分别服从χ2(2)与χ2(1)。
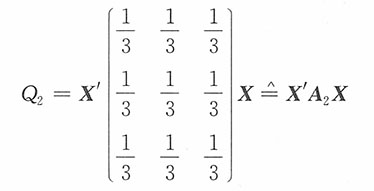
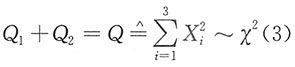 ,n=3,而A1,A2的秩分别为n1=2,n2=1,即n1+n2=3=n。由柯赫伦定理:Q1~χ2(2),Q2~χ2(1),且相互独立。
,n=3,而A1,A2的秩分别为n1=2,n2=1,即n1+n2=3=n。由柯赫伦定理:Q1~χ2(2),Q2~χ2(1),且相互独立。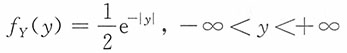
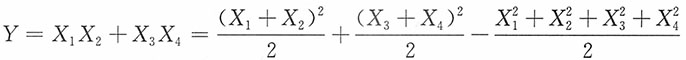
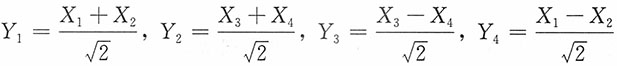
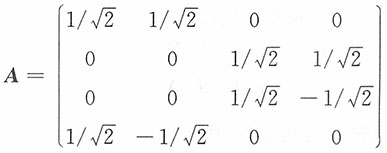

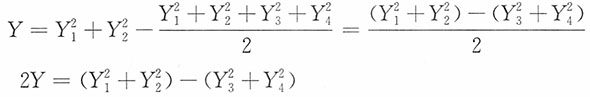
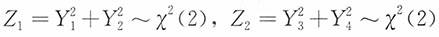 ,且两者独立。
,且两者独立。
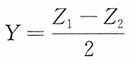 的分布函数
的分布函数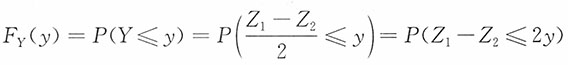

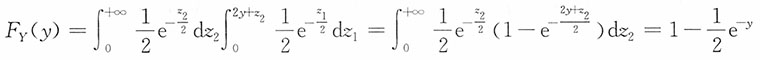
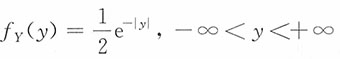
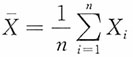 ,
, 。
。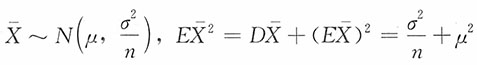 ,又ES2=σ2由此
,又ES2=σ2由此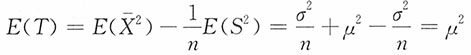
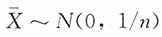 ,(n-1)S2~χ2(n-1),
,(n-1)S2~χ2(n-1),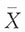 与S2独立,进而
与S2独立,进而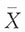 与S2独立。注意到
与S2独立。注意到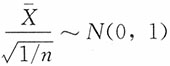 ,进而
,进而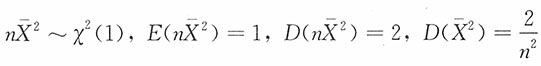 ,又注意到
,又注意到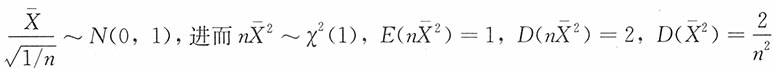 ,又
,又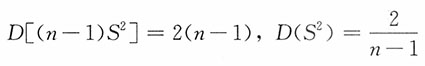
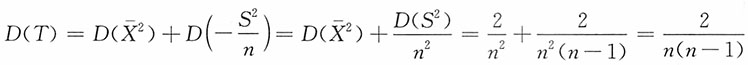
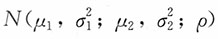 的一个简单随机样本,记
的一个简单随机样本,记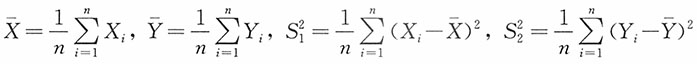
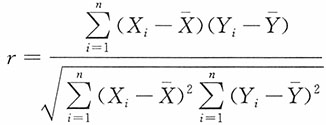 ,求统计量
,求统计量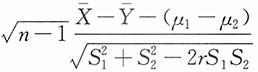 的分布。
的分布。
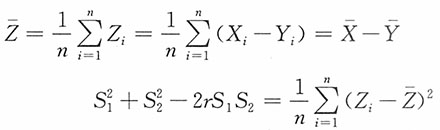
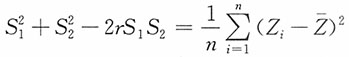
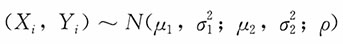 ,i=1,2,…,n,则Xi-Yi也服从正态分布。
,i=1,2,…,n,则Xi-Yi也服从正态分布。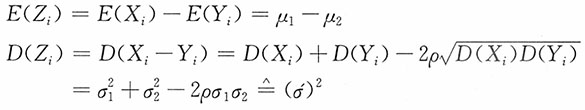
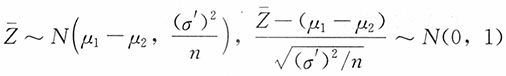 。
。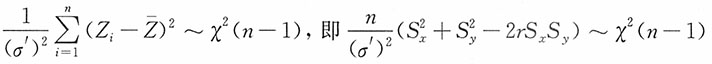
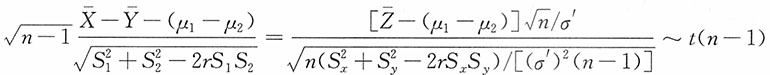
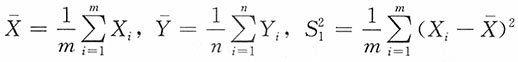 ,
,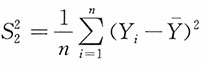 ,而α,β为常数。试求
,而α,β为常数。试求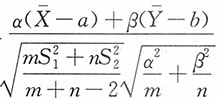 的分布。
的分布。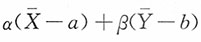 也服从正态分布。
也服从正态分布。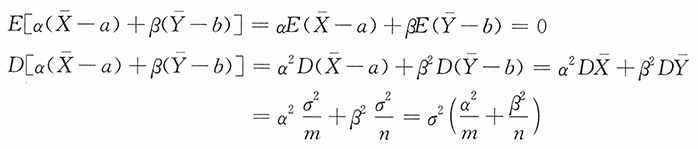
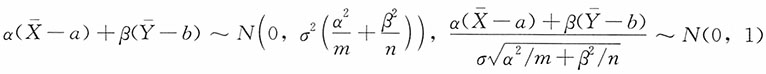 ,而又
,而又 ,且
,且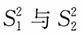 独立,则
独立,则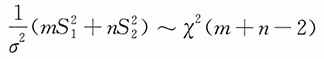
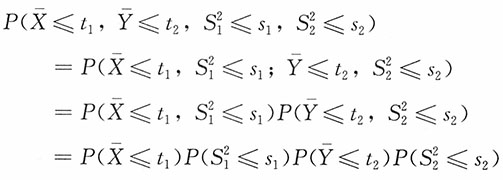
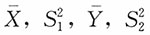 相互独立,进而
相互独立,进而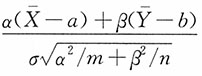 与
与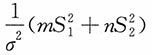 独立,则
独立,则