单项选择题2. 设X
1,X
2,…,X
n,是来自正态总体X~N(μ,σ
2)的样本,则μ
2+σ
2的矩法估计量为______。
A.
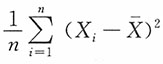
B.
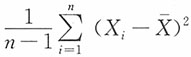
C.
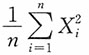
D.
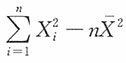
A B C D
4. 设X
1,X
2,…,X
n为来自正态分布N(μ,σ
2)的样本,其中μ为已知,
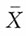
为样本均值,则σ
2的极大似然估计为______。
A.
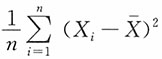
B.

C.
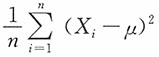
D.
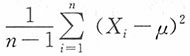
A B C D
5. 设总体X服从参数为λ的泊松分布,λ>0未知,X
1,X
2,…,X
n是总体的一个样本,
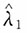
是参数λ的矩估计,
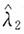
是参数λ的极大似然估计,则
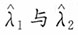
的关系为______。
A.

B.
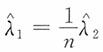
C.
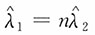
D.
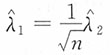
A B C D
8. 设X
1,X
2,…,X
n是来自正态总体N(μ,σ
2)的一个随机样本,μ已知,定义三个统计量如下:
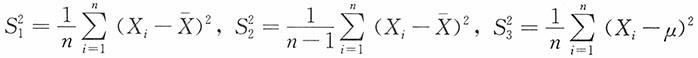
,那么,下面论断中,哪一项成立?______。
A.
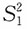
是σ
2的无偏估计
B.S
2是σ的无偏估计
C.S
3是σ的无偏估计
D.
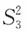
是σ2的无偏估计
A B C D
9. 设样本X
1,X
2,…,X
n是来自正态总体N(μ,σ
2)的样本,则常数C=______时,
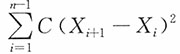
为σ
2的无偏估计。
A.
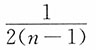
B.
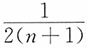
C.
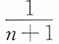
D.
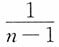
A B C D
11. 设X
1,X
2,X
3,X
4是来自总体X的样本,EX=μ,则______是μ的最有效估计。
A.
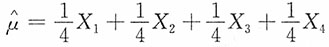
B.
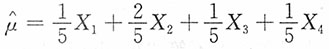
C.
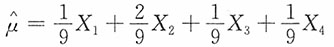
D.
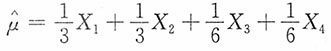
A B C D
15. 设总体X的分布中未知参数θ的置信度为1-α的置信区间为
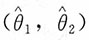
,即
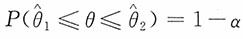
,则下列说法正确的是______。
A.对
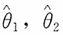
的观测值a,b,恒有θ∈(a,b)
B.θ的数学期望Eθ必属于
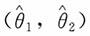
C.θ以1-α的概率落入区间
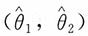
D.区间
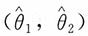
以1-α的概率包含θ
A B C D
37. 设X
1,X
2,…,X
n独立同分布,具有期望μ,则______。
A.
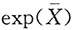
是e
μ的相合估计量
B.
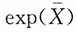
是e
μ的最大似然估计量
C.
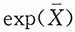
是e
μ的无偏估计量
D.
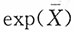
是e
μ的充分统计量
A B C D
A
[解析] 结论:设

是θ的相合估计量,g(x)是连续函数,则
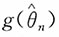
是g(θ)的相合估计量。

,
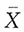
为μ的相合估计,又函数y=e
x为连续函数,则

也为e
μ的相合估计。
38. 假设男子身高服从正态分布,根据调查,2009年上海成年男子身高68%的区间估计为[167.32,175.02],据此推算,99.7%的上海成年男子的身高的区间估计为______。
- A.[161.32,177.02]
- B.[159.62,189.72]
- C.[163.47,178.87]
- D.[155.77,186.57]
A B C D
B
[解析] 假设X~N(μ,σ
2),给定1-α,μ的区间估计为
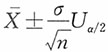
。若取1-α=0.68,U
α/2=1,此时区间估计为

,若置信水平为1-α'=0.997,此时U
α'/2=3,μ的区间估计为
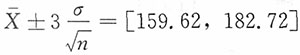
。
39. 已知一总体服从指数分布,其均值为μ,取样本x
1,x
2,…,x
n(n>1),得到样本均值
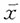
,以下说法错误的是______。
A.μ的矩估计和极大似然估计都是
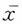
B.
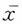
是μ的充分统计量
C.在μ的所有估计中,
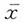
的均方误差最小
D.当样本量趋于无穷时,
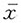
的极限是μ
A B C D
D
[解析] X~Exp(1/μ),EX=μ,即μ的矩估计为
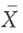
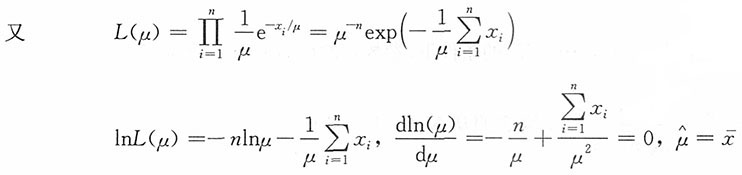
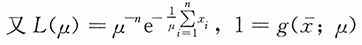
由因子分解定理,
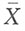
为μ的充分统计量。又
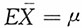
,
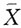
的均方误差即为

的方差
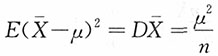
,
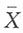
为最小方差的无偏估计,而由大数定律,
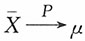
,即依概率收敛于μ,而不是极限μ。
40. 设X
1,X
2,…,X
n是来自正态总体N(μ,σ
2)的一个样本,下列统计量中均方误差最小的是______。
A.
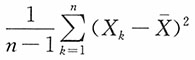
B.
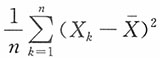
C.
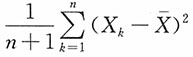
D.

A B C D
41. 设X
1,X
2,…,X
n是来自正态总体N(μ,σ
2)的一个简单随机样本,σ
2的极大似然估计为
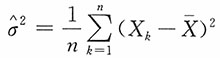
,则
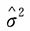
的渐进分布是______。
A.N(σ
2,2σ
4)
B.N(σ
2,σ
4)
C.
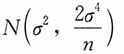
D.
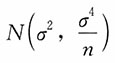
A B C D
C
[解析]
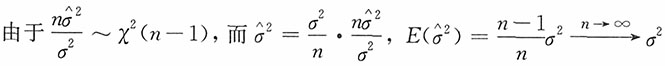
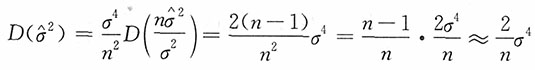
,当n很大时,χ
2(n-1)近似为N(n-1,2(n-1)),则
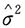
的渐近分布为
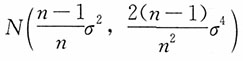
,也即
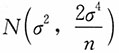
。
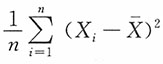
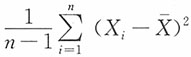
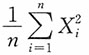
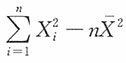
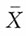 为样本均值,则σ2的极大似然估计为______。
为样本均值,则σ2的极大似然估计为______。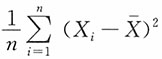

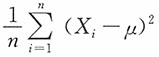
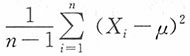
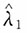 是参数λ的矩估计,
是参数λ的矩估计,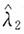 是参数λ的极大似然估计,则
是参数λ的极大似然估计,则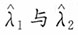 的关系为______。
的关系为______。
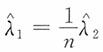
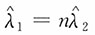
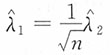
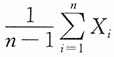
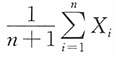
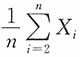
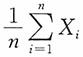
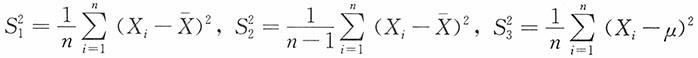 ,那么,下面论断中,哪一项成立?______。
,那么,下面论断中,哪一项成立?______。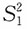 是σ2的无偏估计
是σ2的无偏估计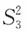 是σ2的无偏估计
是σ2的无偏估计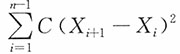 为σ2的无偏估计。
为σ2的无偏估计。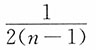
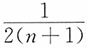
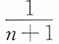
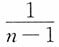
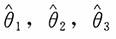 均为参数的无偏估计量,下列对于参数θ的估计量最有效的是______。
均为参数的无偏估计量,下列对于参数θ的估计量最有效的是______。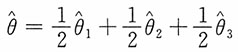
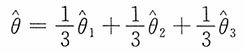
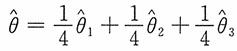
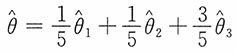
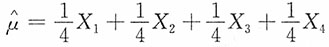
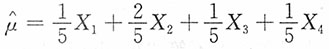
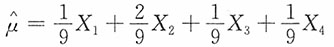
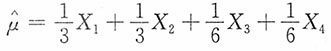
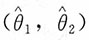 ,即
,即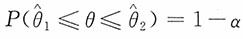 ,则下列说法正确的是______。
,则下列说法正确的是______。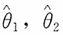 的观测值a,b,恒有θ∈(a,b)
的观测值a,b,恒有θ∈(a,b)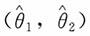
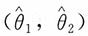
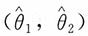 以1-α的概率包含θ
以1-α的概率包含θ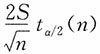
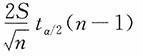
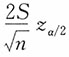
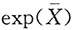 是eμ的相合估计量
是eμ的相合估计量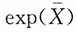 是eμ的最大似然估计量
是eμ的最大似然估计量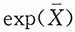 是eμ的无偏估计量
是eμ的无偏估计量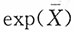 是eμ的充分统计量
是eμ的充分统计量 是θ的相合估计量,g(x)是连续函数,则
是θ的相合估计量,g(x)是连续函数,则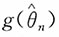 是g(θ)的相合估计量。
是g(θ)的相合估计量。 ,
,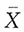 为μ的相合估计,又函数y=ex为连续函数,则
为μ的相合估计,又函数y=ex为连续函数,则 也为eμ的相合估计。
也为eμ的相合估计。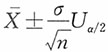 。若取1-α=0.68,Uα/2=1,此时区间估计为
。若取1-α=0.68,Uα/2=1,此时区间估计为 ,若置信水平为1-α'=0.997,此时Uα'/2=3,μ的区间估计为
,若置信水平为1-α'=0.997,此时Uα'/2=3,μ的区间估计为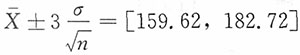 。
。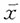 ,以下说法错误的是______。
,以下说法错误的是______。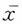
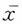 是μ的充分统计量
是μ的充分统计量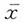 的均方误差最小
的均方误差最小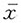 的极限是μ
的极限是μ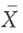
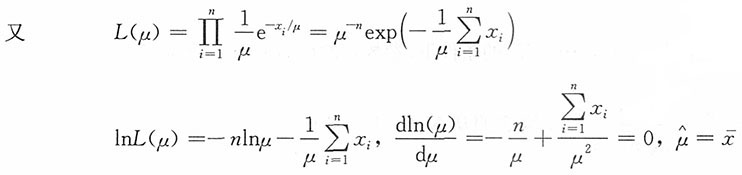
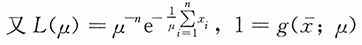 由因子分解定理,
由因子分解定理,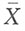 为μ的充分统计量。又
为μ的充分统计量。又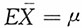 ,
,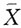 的均方误差即为
的均方误差即为 的方差
的方差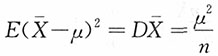 ,
,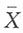 为最小方差的无偏估计,而由大数定律,
为最小方差的无偏估计,而由大数定律,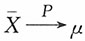 ,即依概率收敛于μ,而不是极限μ。
,即依概率收敛于μ,而不是极限μ。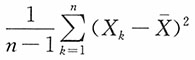
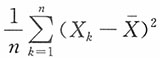
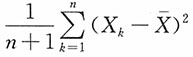

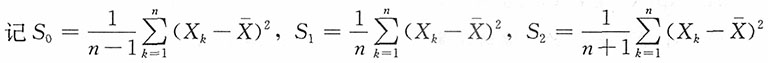
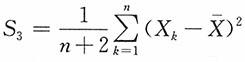 ,由于
,由于 ,则
,则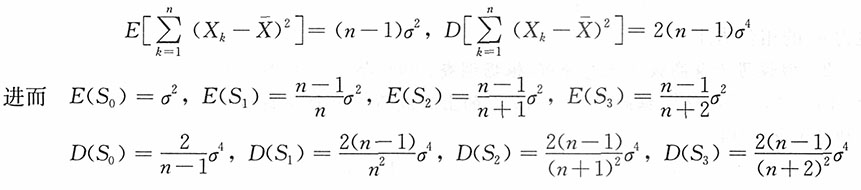
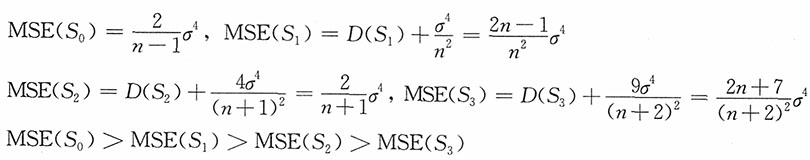
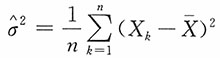 ,则
,则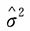 的渐进分布是______。
的渐进分布是______。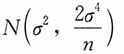
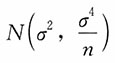
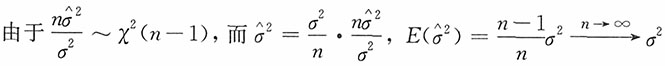
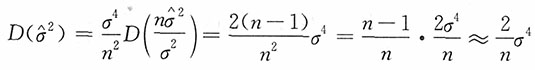 ,当n很大时,χ2(n-1)近似为N(n-1,2(n-1)),则
,当n很大时,χ2(n-1)近似为N(n-1,2(n-1)),则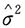 的渐近分布为
的渐近分布为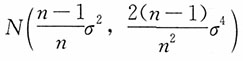 ,也即
,也即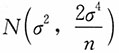 。
。