计算题设X1,X2,…,Xn是来自总体X~U[0,θ]的一个简单随机样本,证明:1.
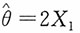
不是θ的相合估计。
证明:
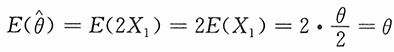
,即
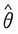
为θ的无偏估计。为证
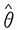
不是θ的相合估计,只需要证明:对任意ε>0,
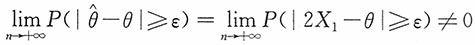
。
注意到|2X
1-θ|≥ε等价于2X
1-θ≥ε或2X
1-θ≤-ε,也即
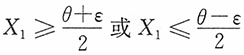
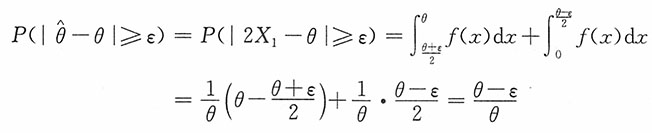
则有
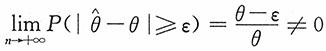
,即
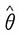
不是θ的相合估计。
2. 对任意给定的常数a,b,
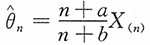
是θ的相合估计。
证明:又由于
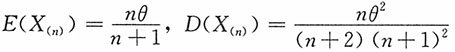
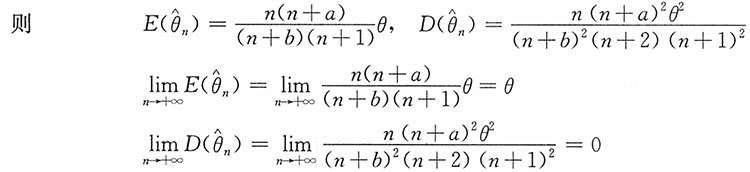
进而由定理可知
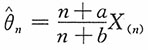
是θ的相合估计。
注 参数θ的极大似然估计X
(n),θ的无偏估计
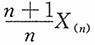
都是θ的相合估计。
3. 设X
1,X
2,…,X
n是取自总体X~U[0,θ]的一个简单随机样本,试证
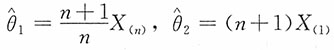
都是θ的无偏估计,并问这两个估计中哪个更有效?
证明:
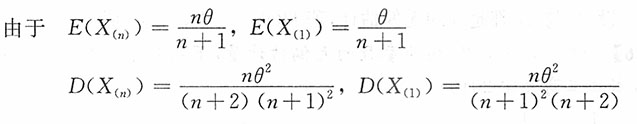
由此,
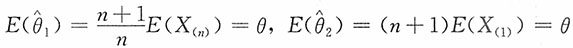
,即
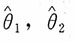
都是θ的无偏估计。
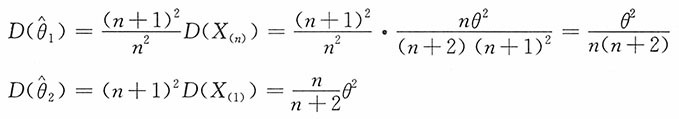
易见,当n>1时,有
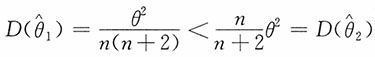
,即
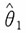
的方差较小,其更有效。
4. 设X
1,X
2…X
n是取自总体
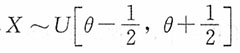
的一个简单随机样本,试证
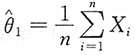
和
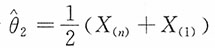
都是θ的无偏估计,并问这两个估计中哪个更有效?
证明:易知
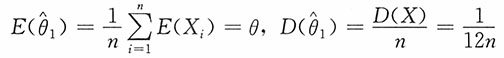

当n≤2时,
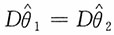
;而当n>2时,
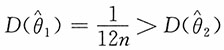
,故
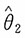
更有效。
5. 设X
1,X
2,…,X
n是来自总体X~N[0,θ]的一个简单随机样本,θ的极大似然估计
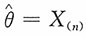
,而其无偏估计
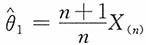
,其均方误差
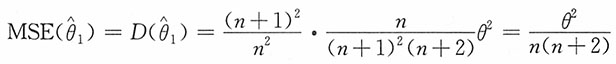
解:现考虑如下形式
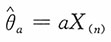
的估计,其均方误差
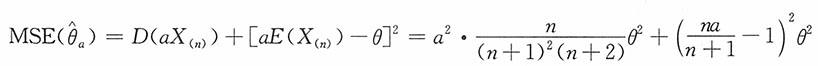
当a取
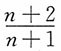
时,上述均方误差达到最小值,且
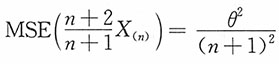
,这表明
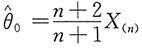
虽为θ的有偏估计,但其均方误差
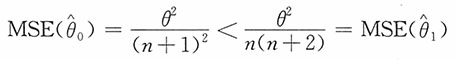
即在此均方误差的标准下,有偏估计
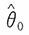
优于无偏估计
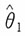
。
6. 设X
1,X
2,…,X
n来自正态总体X~N(μ,σ
2)的一个简单随机样本,由于
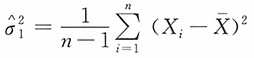
是σ
2的无偏估计量,
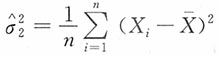
是σ
2的极大似然估计。求在σ
2的估计类
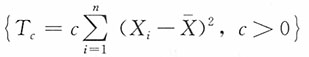
中具有最小均方误差的σ
2的估计量。
解:由于

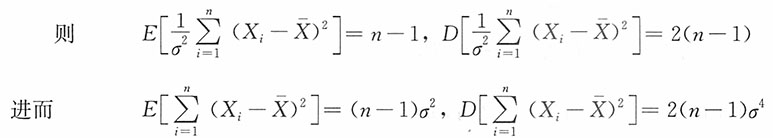
MSE(T
c)=D(T
c)+[E(T
c)-σ
2]
2=2c
2(n-1)σ
4+[c(n-1)σ
2-σ
2]
2 ={2c
2(n-1)+[c(n-1)-1]
2}σ
4 令函数g(c)=2c
2(n-1)+[c(n-1)-1]
2,c>0
g'(c)=4c(n-1)+2[c(n-1)-1](n-1)=0,并令g'(c)=0,解得
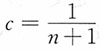
又
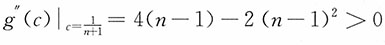
,则当

时,g(c)取得最小值。
由此,在此估计类中具有最小均方误差的σ
2的估计量为
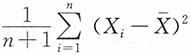
。
7. 设正态总体X~N(0,σ
2),从中抽取容量为4的随机枰本X
1,X
2,X
3,X
4,
令
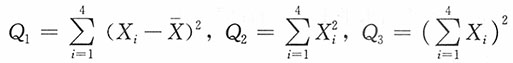
(1)分别求常数b
1,b
2,b
3,使b
1Q
1,b
2Q
2,b
3Q
3是方差σ
2的无偏估计量。
(2)比较(1)中3个无偏估计量的优劣。
(3)基于Q
2构建σ
2的一个95%的置信区间。
解:(1)

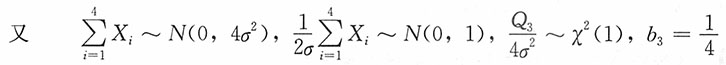
(2)
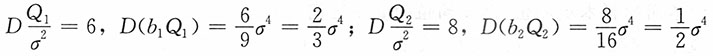
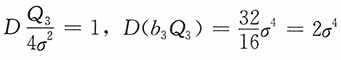
,即b
2Q
2更有效。
(3)
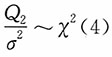
,于是有
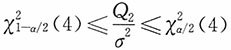
,则σ
2在95%置信水平下的置信区间为
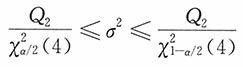
两个独立样本的均值和标准差 
8. 设n
1=n
2=100,求μ
1-μ
2的95%的置信区间。
解:由于两个样本均为独立大样本,
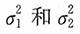
未知。当α=0.05时,z
0.05/2=1.96,μ
1-μ
2的95%的置信区间为
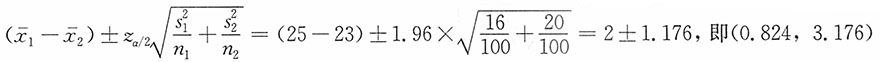
9. 设n
1=n
2=10,
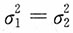
,求μ
1-μ
2的95%的置信区间。
解:由于两个样本均为来自正态总体的独立小样本,当
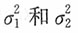
未知但相等时,
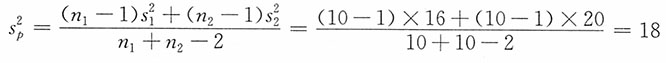
当α=0.05时,t
0.05/2(10+10-2)=2.101,μ
1-μ
2的95%的置信区间为
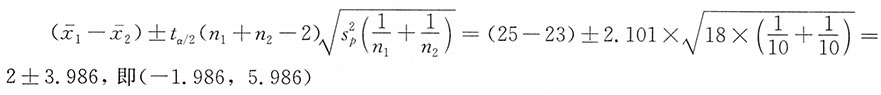
10. 设n
1=n
2=10,
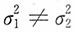
,求μ
1-μ
2的95%的置信区间。
解:由于两个样本均为来自正态总体的独立小样本,
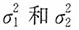
未知且不相等,n
1=n
2=10。因此,μ
1-μ
2的95%的置信区间为
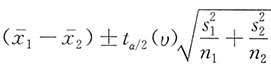
。自由度的计算如下:
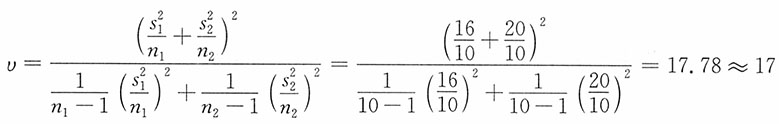
当α=0.05时,t
0.05/2(17)=2.11。μ
1-μ
2的95%的置信区间为
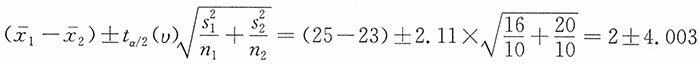
,即(-2.003,6.003)
11. 设n
1=10,n
2=20,
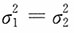
,求μ
1-μ
2的95%的置信区间。
解:由于两个样本均为来自正态总体的独立小样本,
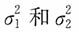
未知但相等,n
1≠n
2。此时
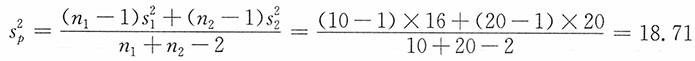
当α=0.05时,t
0.05/2(10+20-2)=2.048。μ
1-μ
2的95%的置信区间为
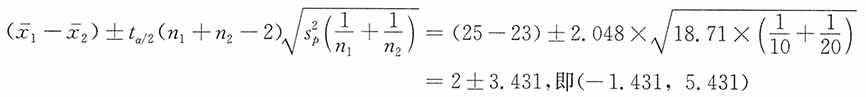
12. 设n
1=10,n
2=20,
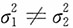
,求μ
1-μ
2的95%的置信区间。
解:由于两个样本均为来自正态总体的独立小样本,
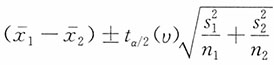
。未知且不相等,n
1≠n
2。因此,μ
1-μ
2的95%的置信区间为
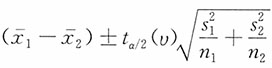
。自由度的计算如下:
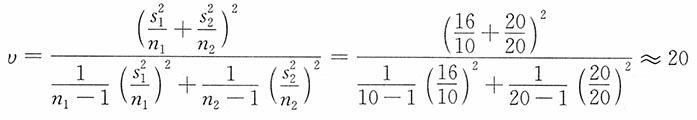
当α=0.05时,t
0.05/2(20)=2.086。μ
1-μ
2的95%的置信区间为
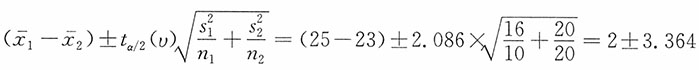
,即(-1.364,5.364)
13. 由10名学生组成一个随机样本,让他们分别采用A和B两套试卷进行测试,结果如表所示。
| 测试结果对比 |
| 学生编号 | 试卷A | 试卷B | 差值d |
| l | 78 | 71 | 7 |
| 2 | 63 | 44 | 19 |
| 3 | 72 | 61 | 11 |
| 4 | 89 | 84 | 5 |
| 5 | 91 | 74 | 17 |
| 6 | 49 | 51 | -2 |
| 7 | 68 | 55 | 13 |
| 8 | 76 | 60 | 16 |
| 9 | 85 | 77 | 8 |
| 10 | 55 | 39 | 16 |
假定两套试卷分数之差服从正态分布,试建立两套试卷平均分数之差μ
d=μ
1-μ
2的95%的置信区间。
解:计算得
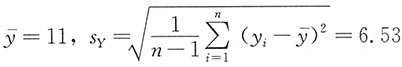
,而t
0.025(9)=2.2622,则两套试卷平均分数之差μ
d=μ
1-μ
2的95%的置信区间为
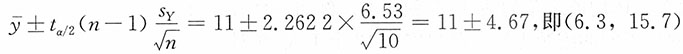
两套试卷平均分数之差的95%的置信区间为6.3分~15.7分。
14. 设X
1,X
2,…,X
n是取自
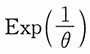
的一个简单随机样本,求e
-θ的置信水平为1-α的单侧置信下限。
解:由于对i=1,2,…,n,
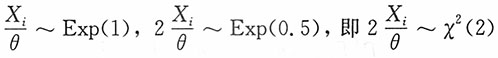
,且
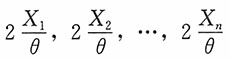
相互独立,则
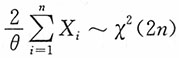
。
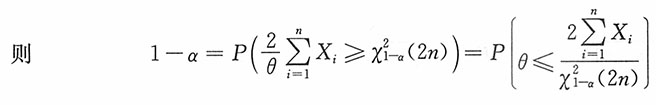
即θ的置信水平为1-α的置信上限为
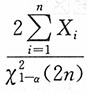
,而e
-θ的置信水平为1-α的置信下限为
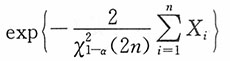
15. 设X
(1),X
(2),…,X
(n)为来自两参数指数分布总体X~Exp(μ,1/θ)的一个容量为n的前n个次序统计量,总体的密度函数为
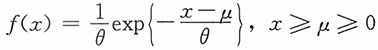
,θ>0,给定显著性水平α,求参数μ,θ的置信水平1-α的置信区间。
解:令
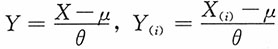
,i=1,2,…,n,则Y
(1),Y
(2),…,Y
(n)与来自标准指数分布Exp(1)的容量为n的前n个次序统计量同分布。
易见,nY
(1),(n-1)(Y
(2)-Y
(1)),…,(Y
(n)-Y
(n-1))相互独立且同服从标准指数分布Exp(1),进而2nY
(1),2(n-1)(Y
(2)-Y
(1)),…,2(Y
(n)-Y
(n-1))相互独立且同服从χ2(2)
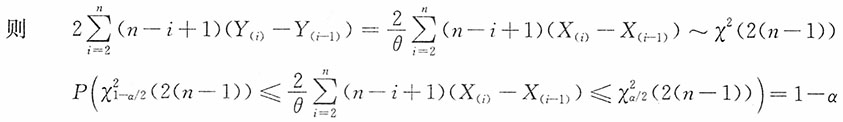
进而θ的置信水平1-α的置信区间为:
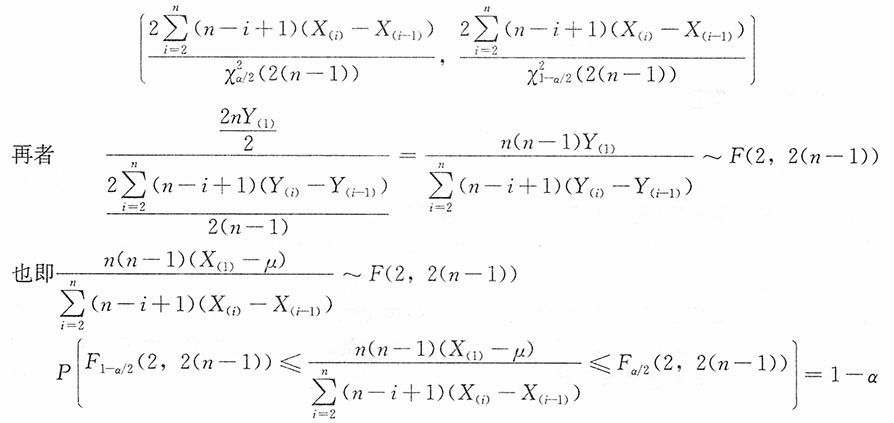
则参数μ的置信水平1-α的置信区间为

也可以进行如下方式处理:
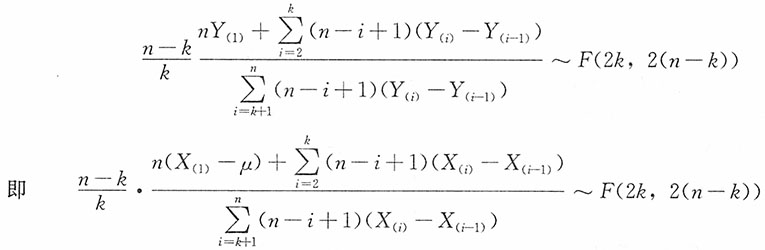
而k取值通常取为
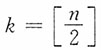
16. 某居民小区有居民500户,小区管理者准备采用一项新的供水设施,想了解居民是否赞成。管理者采取重复抽样方法随机抽取了50户,其中有32户赞成,18户反对。(1)当置信水平为95%时,求总体中赞成该项改革的户数比率的置信区间。(2)如果管理者预计赞成的比率能达到80%,置信水平为95%时,要求允许误差不超过10%,应抽取多少户进行调查?
解:(1)样本容量n=50>30,可视为是一个大样本,由中心极限定理知,总体中赞成该项改革的户数比率π的抽样分布近似服从均值为p,方差为p(1-p)/n的正态分布。此时可用样本方差来代替总体方差,则总体中赞成该项改革的户数比率95%的置信区间为
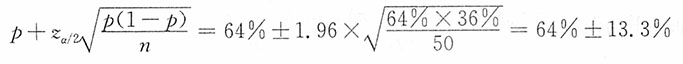
即总体中赞成该项改革的户数比率95%置信区间为(50.7%,77.3%)。
(2)允许误差范围为不超过10%,即
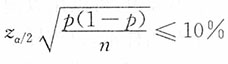
,解得n≥62,说明要求允许误差不超过10%,至少应抽取62户进行调查。
17. 设某批产品的废品率为p,从这批产品中抽取一个样本X
1,X
2,…,X
n,取p的先验分布π(p)为[0,1]上的均匀分布,求p的贝叶斯估计。
解:
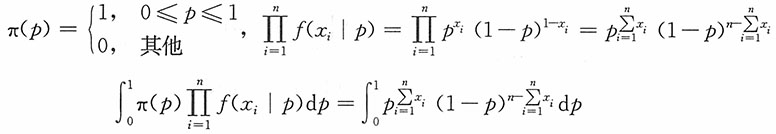
由贝塔函数
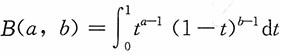
的定义及性质

,得
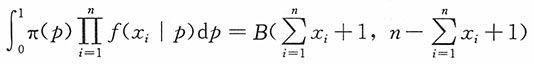
所以p的后验分布为
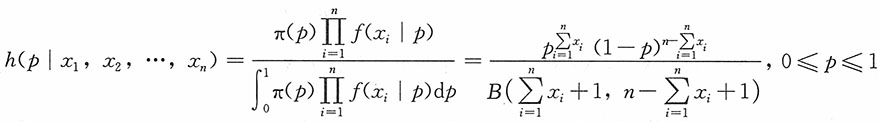
因此p的贝叶斯估计
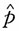
为
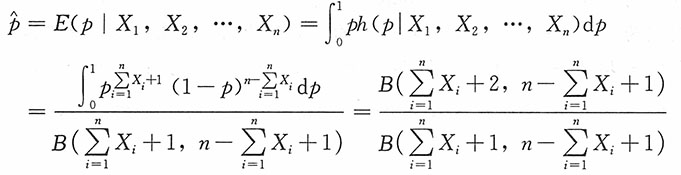
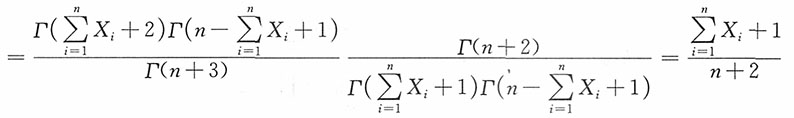 注
注 用经典方法构造的p的估计
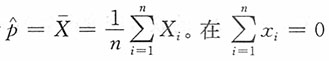
时(即样本中无废品时),估计
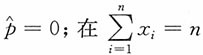
时(即样本中均是废品时),估计
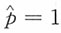
。这样的估计似乎太极端了,有点不切实际,但当样本容量n较小时这样的情形难以避免。而按贝叶斯估计
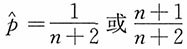
这样的估计留有余地,给人以比较可靠之感。这个例子也是贝叶斯方法受到人们重视的一个原因。
18. 设总体X~N(μ,σ
2),σ
2已知,X
1,X
2,…,X
n是来自总体X的一个简单随机样本,取π(μ)=1,-∞<μ<+∞,求μ的贝叶斯估计。
19. 已知某种电视机的寿命服从指数分布密度,
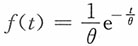
,其中θ>0为电视机的平均寿命(原题用的符号为λ),现在随机抽取n台进行寿命测试,试验到第r台失效为止,并且这些失效时间为t
1≤t
2≤…≤t
r,其余n-r台直到试验结束还未失效。请回答下列问题:(1)求电视机平均寿命θ的极大似然估计。(2)若θ的先验分布为
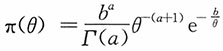
,其中,θ>0,a>0,b>0,求电视机平均寿命θ的贝叶斯估计。
解:(1)似然函数为
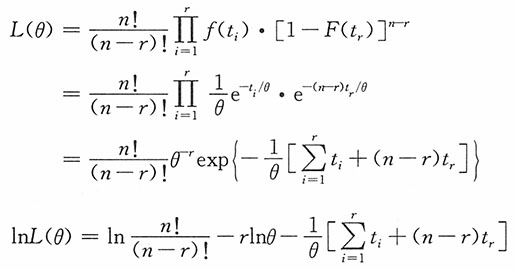

则参数θ的极大似然估计为
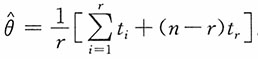
。
(2)后验密度函数为
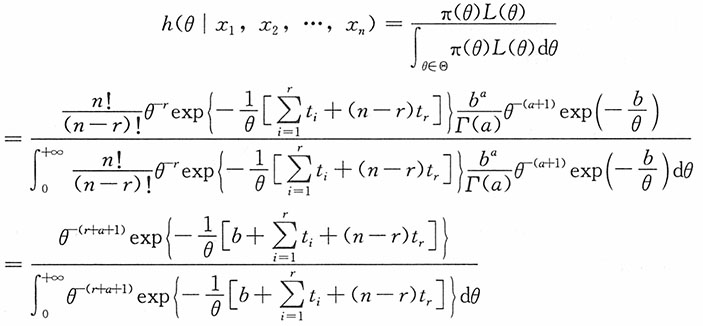

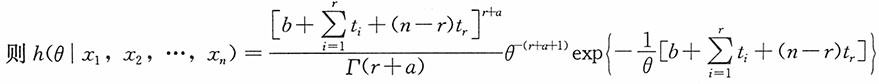
进而θ的贝叶斯估计为
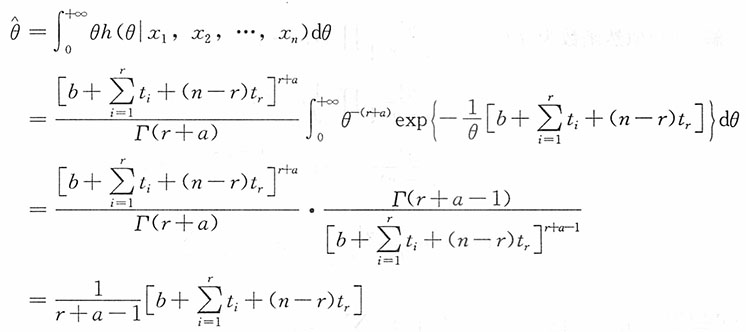
20. 设总体
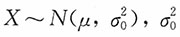
已知,X
1,X
2,…,X
n是来自总体X的一个简单随机样本,取π(μ)=1,-∞<μ<+∞,求μ的贝叶斯置信区间。
解:可知,在题设条件下μ的后验分布为
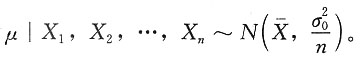
所以
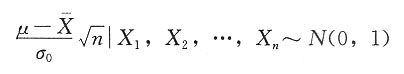
由
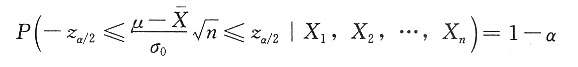
得
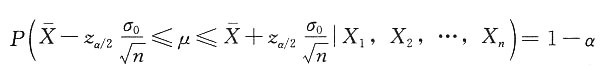
μ的贝叶斯区间估计为
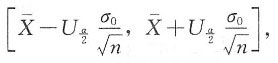
与经典方法得到的一致。
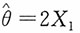 不是θ的相合估计。
不是θ的相合估计。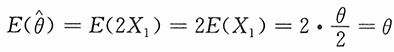 ,即
,即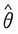 为θ的无偏估计。为证
为θ的无偏估计。为证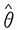 不是θ的相合估计,只需要证明:对任意ε>0,
不是θ的相合估计,只需要证明:对任意ε>0,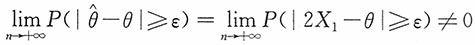 。
。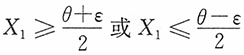
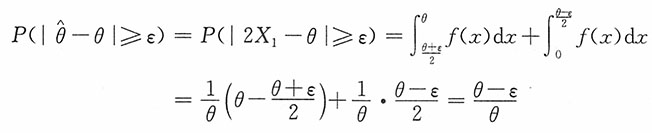
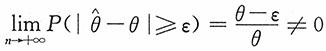 ,即
,即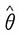 不是θ的相合估计。
不是θ的相合估计。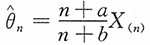 是θ的相合估计。
是θ的相合估计。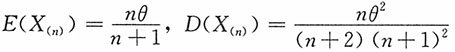
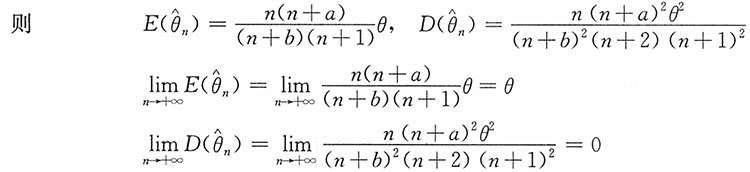
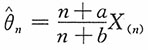 是θ的相合估计。
是θ的相合估计。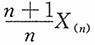 都是θ的相合估计。
都是θ的相合估计。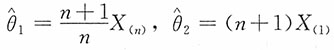 都是θ的无偏估计,并问这两个估计中哪个更有效?
都是θ的无偏估计,并问这两个估计中哪个更有效?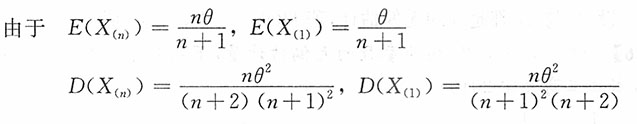
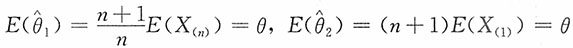 ,即
,即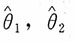 都是θ的无偏估计。
都是θ的无偏估计。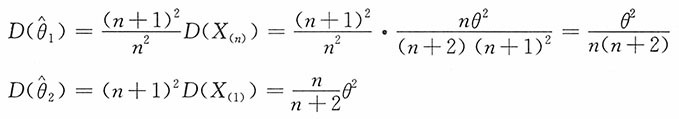
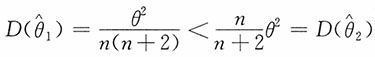 ,即
,即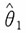 的方差较小,其更有效。
的方差较小,其更有效。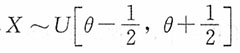 的一个简单随机样本,试证
的一个简单随机样本,试证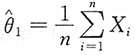 和
和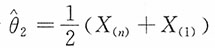 都是θ的无偏估计,并问这两个估计中哪个更有效?
都是θ的无偏估计,并问这两个估计中哪个更有效?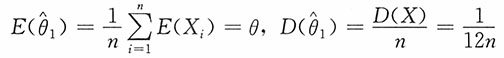

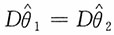 ;而当n>2时,
;而当n>2时,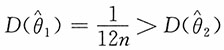 ,故
,故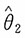 更有效。
更有效。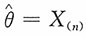 ,而其无偏估计
,而其无偏估计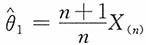 ,其均方误差
,其均方误差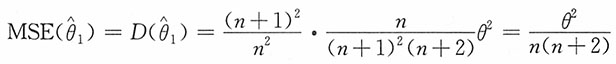
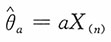 的估计,其均方误差
的估计,其均方误差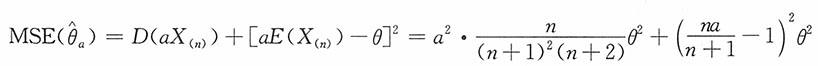
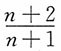 时,上述均方误差达到最小值,且
时,上述均方误差达到最小值,且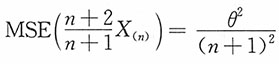 ,这表明
,这表明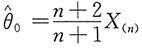 虽为θ的有偏估计,但其均方误差
虽为θ的有偏估计,但其均方误差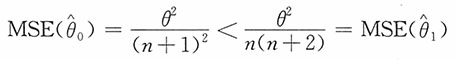
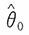 优于无偏估计
优于无偏估计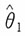 。
。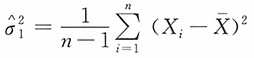 是σ2的无偏估计量,
是σ2的无偏估计量,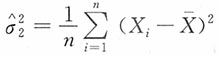 是σ2的极大似然估计。求在σ2的估计类
是σ2的极大似然估计。求在σ2的估计类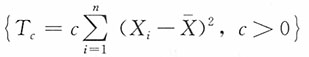 中具有最小均方误差的σ2的估计量。
中具有最小均方误差的σ2的估计量。
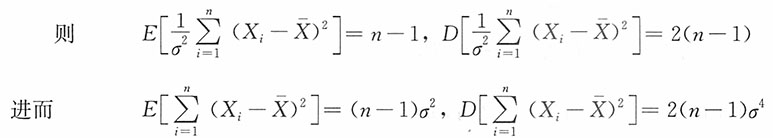
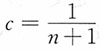
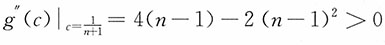 ,则当
,则当 时,g(c)取得最小值。
时,g(c)取得最小值。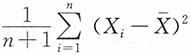 。
。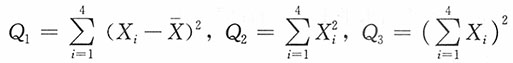

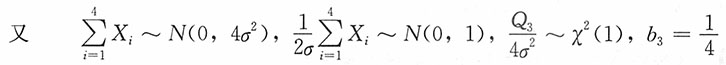
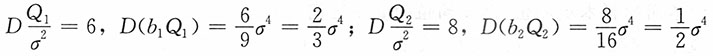
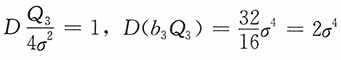 ,即b2Q2更有效。
,即b2Q2更有效。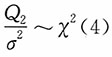 ,于是有
,于是有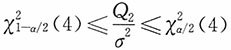 ,则σ2在95%置信水平下的置信区间为
,则σ2在95%置信水平下的置信区间为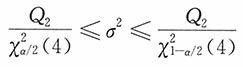

 未知。当α=0.05时,z0.05/2=1.96,μ1-μ2的95%的置信区间为
未知。当α=0.05时,z0.05/2=1.96,μ1-μ2的95%的置信区间为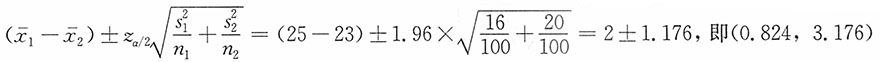
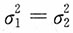 ,求μ1-μ2的95%的置信区间。
,求μ1-μ2的95%的置信区间。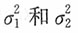 未知但相等时,
未知但相等时,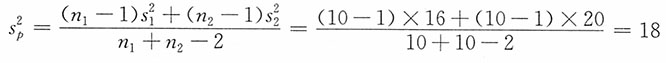
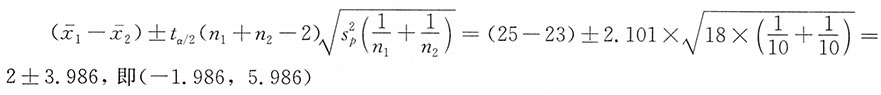
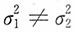 ,求μ1-μ2的95%的置信区间。
,求μ1-μ2的95%的置信区间。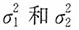 未知且不相等,n1=n2=10。因此,μ1-μ2的95%的置信区间为
未知且不相等,n1=n2=10。因此,μ1-μ2的95%的置信区间为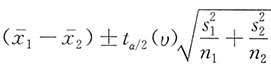 。自由度的计算如下:
。自由度的计算如下: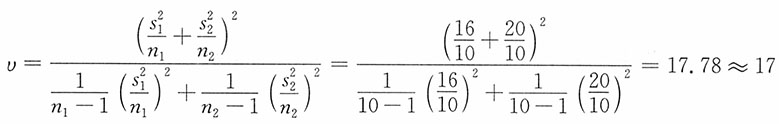
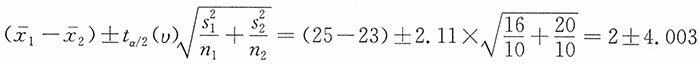 ,即(-2.003,6.003)
,即(-2.003,6.003) ,求μ1-μ2的95%的置信区间。
,求μ1-μ2的95%的置信区间。 未知但相等,n1≠n2。此时
未知但相等,n1≠n2。此时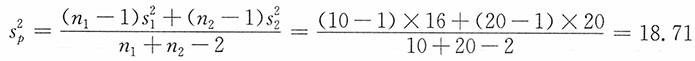
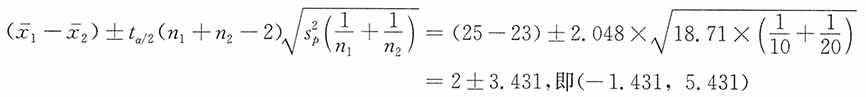
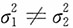 ,求μ1-μ2的95%的置信区间。
,求μ1-μ2的95%的置信区间。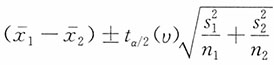 。未知且不相等,n1≠n2。因此,μ1-μ2的95%的置信区间为
。未知且不相等,n1≠n2。因此,μ1-μ2的95%的置信区间为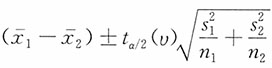 。自由度的计算如下:
。自由度的计算如下: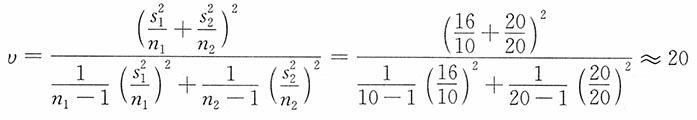
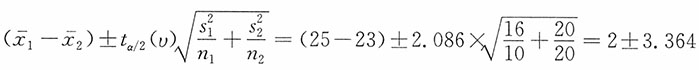 ,即(-1.364,5.364)
,即(-1.364,5.364)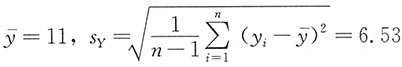 ,而t0.025(9)=2.2622,则两套试卷平均分数之差μd=μ1-μ2的95%的置信区间为
,而t0.025(9)=2.2622,则两套试卷平均分数之差μd=μ1-μ2的95%的置信区间为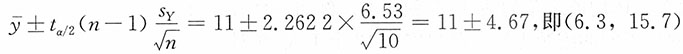 两套试卷平均分数之差的95%的置信区间为6.3分~15.7分。
两套试卷平均分数之差的95%的置信区间为6.3分~15.7分。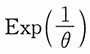 的一个简单随机样本,求e-θ的置信水平为1-α的单侧置信下限。
的一个简单随机样本,求e-θ的置信水平为1-α的单侧置信下限。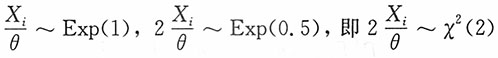 ,且
,且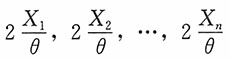 相互独立,则
相互独立,则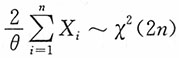 。
。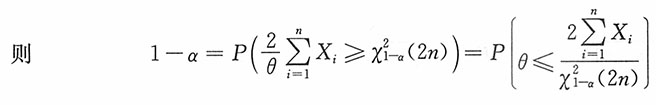
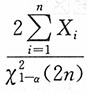 ,而e-θ的置信水平为1-α的置信下限为
,而e-θ的置信水平为1-α的置信下限为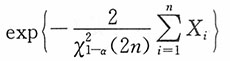
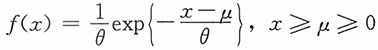 ,θ>0,给定显著性水平α,求参数μ,θ的置信水平1-α的置信区间。
,θ>0,给定显著性水平α,求参数μ,θ的置信水平1-α的置信区间。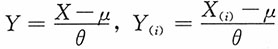 ,i=1,2,…,n,则Y(1),Y(2),…,Y(n)与来自标准指数分布Exp(1)的容量为n的前n个次序统计量同分布。
,i=1,2,…,n,则Y(1),Y(2),…,Y(n)与来自标准指数分布Exp(1)的容量为n的前n个次序统计量同分布。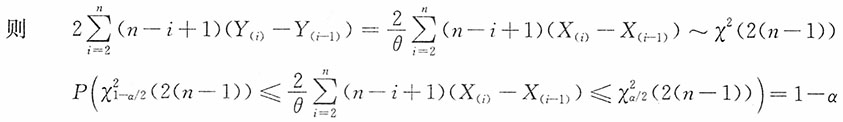

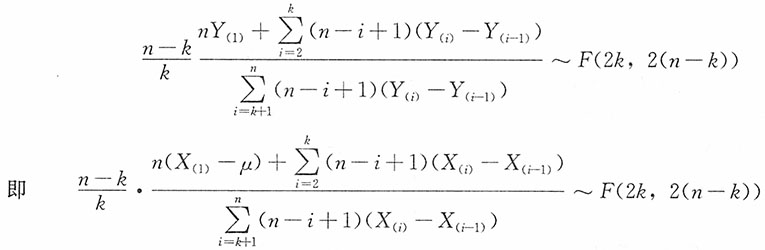
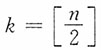
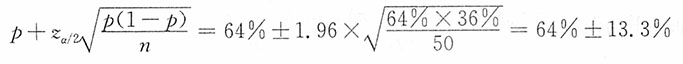
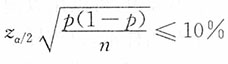 ,解得n≥62,说明要求允许误差不超过10%,至少应抽取62户进行调查。
,解得n≥62,说明要求允许误差不超过10%,至少应抽取62户进行调查。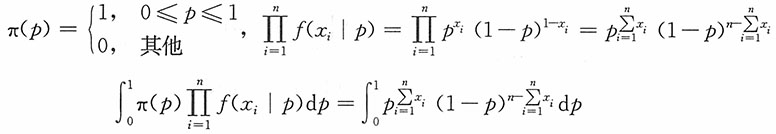
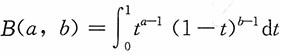 的定义及性质
的定义及性质 ,得
,得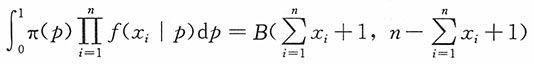
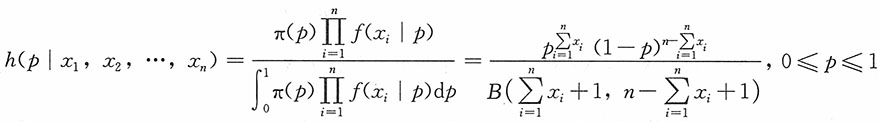
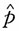 为
为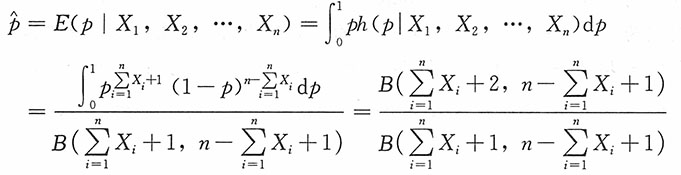
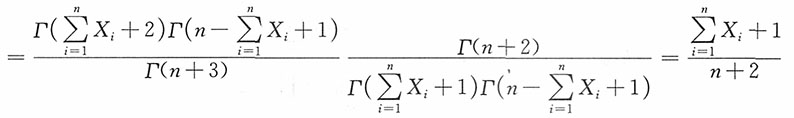
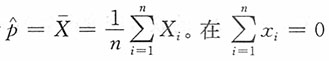 时(即样本中无废品时),估计
时(即样本中无废品时),估计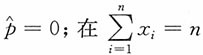 时(即样本中均是废品时),估计
时(即样本中均是废品时),估计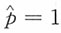 。这样的估计似乎太极端了,有点不切实际,但当样本容量n较小时这样的情形难以避免。而按贝叶斯估计
。这样的估计似乎太极端了,有点不切实际,但当样本容量n较小时这样的情形难以避免。而按贝叶斯估计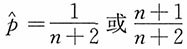 这样的估计留有余地,给人以比较可靠之感。这个例子也是贝叶斯方法受到人们重视的一个原因。
这样的估计留有余地,给人以比较可靠之感。这个例子也是贝叶斯方法受到人们重视的一个原因。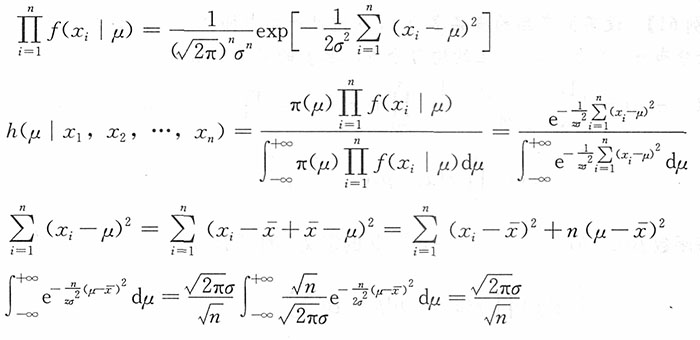
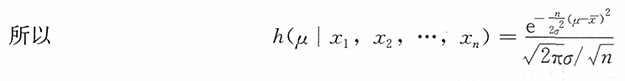
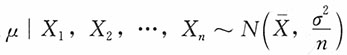 ,μ的贝叶斯估计为
,μ的贝叶斯估计为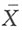 。
。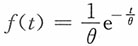 ,其中θ>0为电视机的平均寿命(原题用的符号为λ),现在随机抽取n台进行寿命测试,试验到第r台失效为止,并且这些失效时间为t1≤t2≤…≤tr,其余n-r台直到试验结束还未失效。请回答下列问题:(1)求电视机平均寿命θ的极大似然估计。(2)若θ的先验分布为
,其中θ>0为电视机的平均寿命(原题用的符号为λ),现在随机抽取n台进行寿命测试,试验到第r台失效为止,并且这些失效时间为t1≤t2≤…≤tr,其余n-r台直到试验结束还未失效。请回答下列问题:(1)求电视机平均寿命θ的极大似然估计。(2)若θ的先验分布为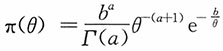 ,其中,θ>0,a>0,b>0,求电视机平均寿命θ的贝叶斯估计。
,其中,θ>0,a>0,b>0,求电视机平均寿命θ的贝叶斯估计。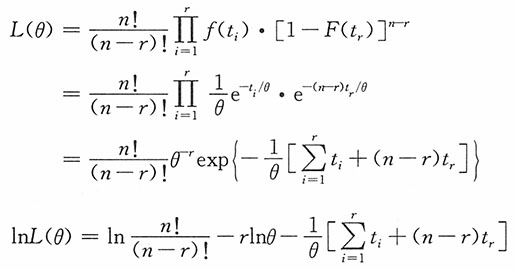

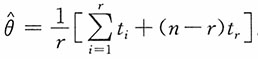 。
。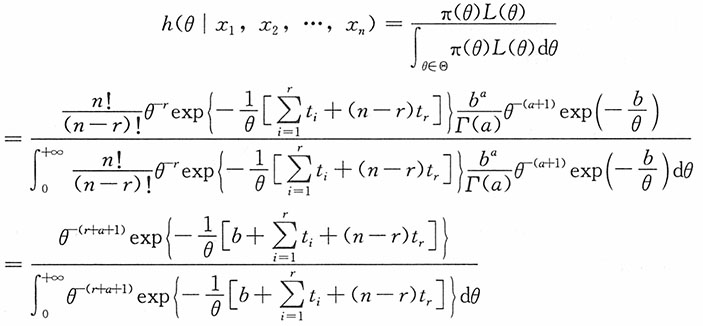

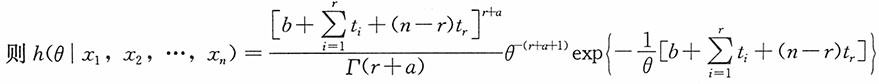
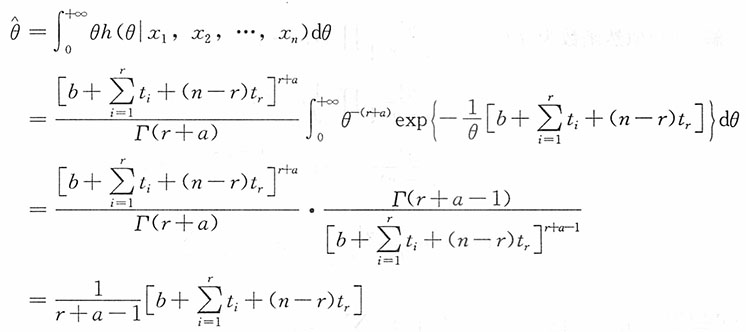
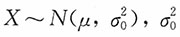 已知,X1,X2,…,Xn是来自总体X的一个简单随机样本,取π(μ)=1,-∞<μ<+∞,求μ的贝叶斯置信区间。
已知,X1,X2,…,Xn是来自总体X的一个简单随机样本,取π(μ)=1,-∞<μ<+∞,求μ的贝叶斯置信区间。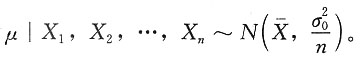
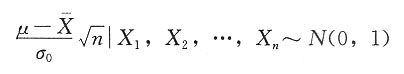
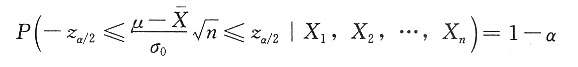
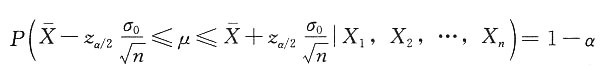
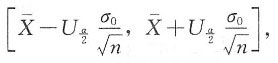 与经典方法得到的一致。
与经典方法得到的一致。