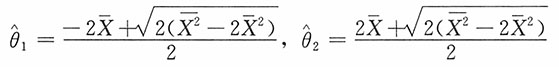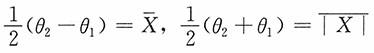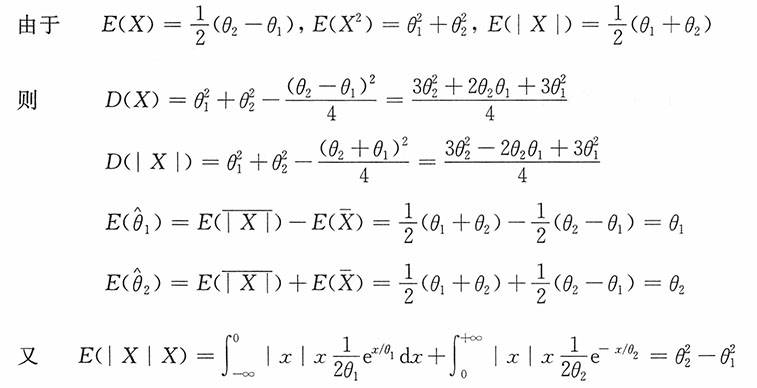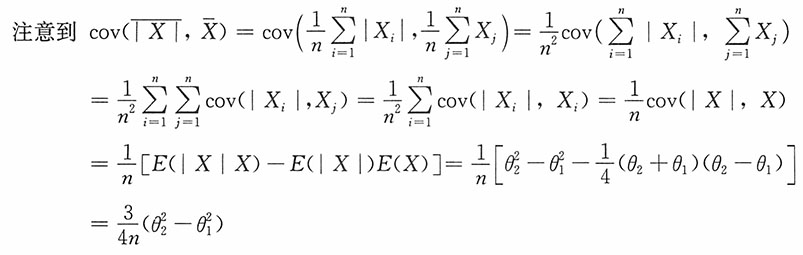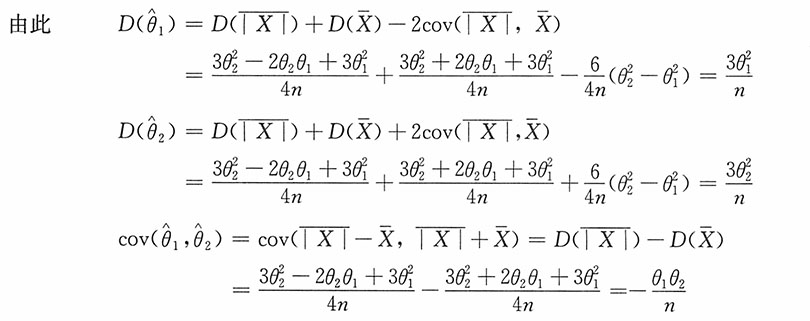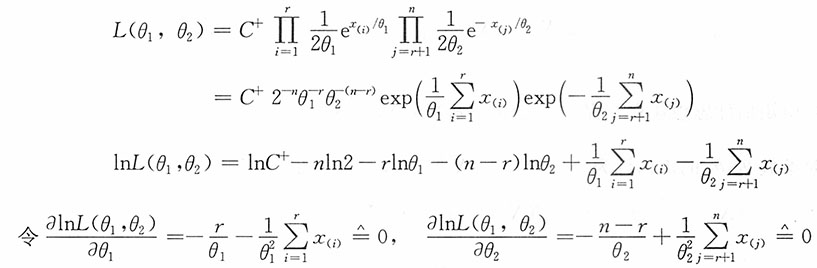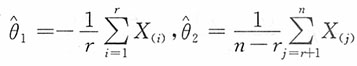计算题1. 从正态总体X~N(μ,σ
2)中抽取容量为n的样木,试证明:若σ已知,则在关于μ的置信度为0.95的置信区间中,
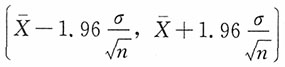
是最短的。
事实上证明如下结论:设总体X~N(μ,σ
2),X
1,X
2…X
n为总体X的一个简单随机样本,在给定置信水平1-α下,
(1)若方差
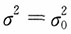
已知时,利用枢轴量
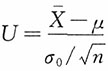
求得的均值μ的区间估计中的最短区间估计为
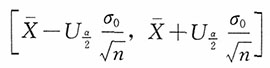
(2)方差σ
2未知时,利用枢轴量
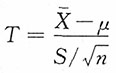
求得的均值μ的区间估计中的最短区间估计为
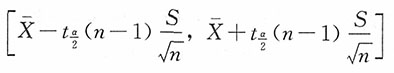
证明:仅(1)考虑到t(n-1)分布与标准正态分布密度函数图形类似,其密度函数曲线单峰且y轴对称,所以(2)完全可类似于(1)给出证明。
由于
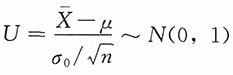
,选取a,b,a<b,使
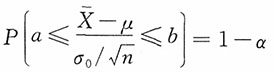
于是
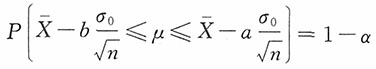
则均值μ的置信水平为1-α的置信区间为
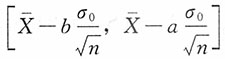
,而此区间的平均长度为
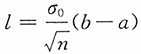
,选取a,b,使L达到最小。
又1-α=P(a≤U≤b)=Φ(b)-Φ(a),其中记Φ(x),φ(x)分别为标准正态分布N(0,1)的分布函数和密度函数。
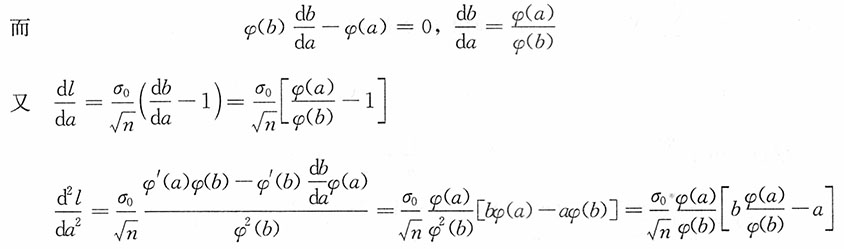
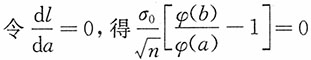
,从中解得φ(a)=φ(b)。考虑到N(0,1)的密度函数单峰且y轴对称,又a<b,则a<b,b>0,b=-a。
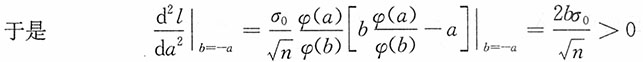
即在a<0,b>0,b=-a下,
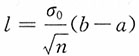
取极小值。进而可得
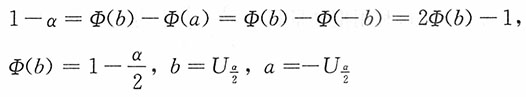
即均值μ的置信水平为1-α的最短的区间估计为
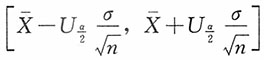
。
2. 为研究儿童看电视的习惯,社会学家从10000名儿童中无放回地随机抽取n=50个儿童作为样本,得到每周看电视的平均时间为12.5小时,样本标准差为2.2小时;样本中男孩为27名。
(1)估计儿童每周平均看电视时间的95%的置信区间。
(2)估计总体中男孩人数的95%的置信区间。
(3)在(1)中,若总体人数为500人,其他条件不变,相应的置信区间是多少?
(4)在(1)中,若平均看电视时间的允许误差(即抽样极限误差)缩小为原来的一半,应抽取多少儿童作为样本?(已知:Z
0.025=1.96)
解:(1)已知n=50属大样本,置信水平1-α=95%,Z
α/2=1.96。
又
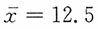
,s=2.2,则儿童每周平均看电视时间的95%的置信区间为
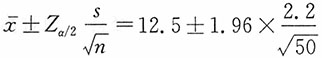
,即12.5±0.61=(11.9,13.1),即11.9~13.1小时。
(2)已知n=50,1-α=95%,样本比例为
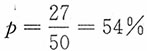
,用样本比例p来代替总体比例π,则总体比例的置信区间可表示为
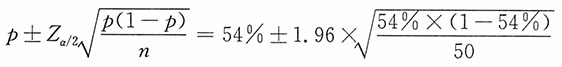
即54%±7.05%=(46.95%,61.05%),总体中男孩人数的95%的置信区间为(46.95%×10000,61.05%×10000),即4695~6105名。
(3)其他条件不变,即仍从500名儿童中无放回随机抽取n=50个儿童作为样本。在大样本情况下,其样本均值的抽样分布仍然服从正态分布,因此置信区间不变,为(11.9,13.1)。
(4)记允许误差为d,则样本量计算公式为
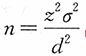
,总体方差未知,用样本方差代替,即为
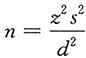
。若d缩小为原来的一半,则n扩大为原来的4倍,即为200个。
 -∞<θ<+∞,X1,X2,…,Xn为其子样。
-∞<θ<+∞,X1,X2,…,Xn为其子样。3. 求参数θ的极大似然估计。
解:似然函数为
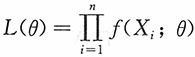
。易见当
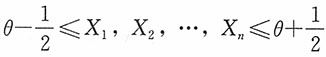
时,L(θ)取到最大值1,此时
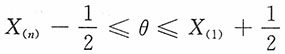
,于是参数θ的极大似然估计为

中的任何值。
4. 证明子样平均
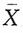
及

都是θ的无偏估计量,问哪个较有效?
解:由于
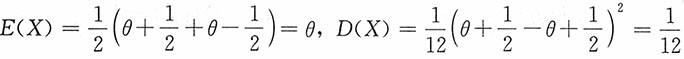
,则
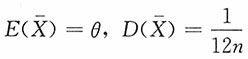
注意到有如下结论:
设总体X~N[θ
1,θ
2],则
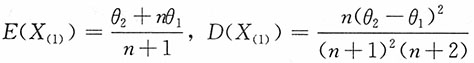
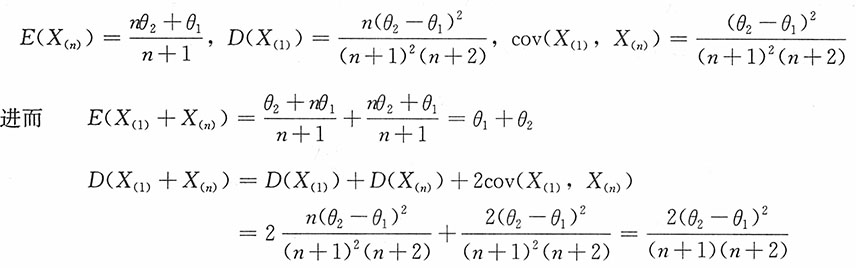
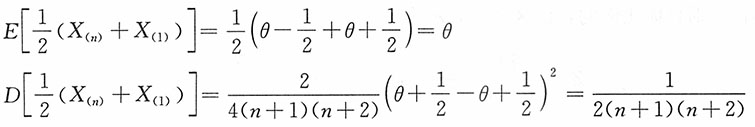
易见,n=1,2时两者相等,而当n>2时,
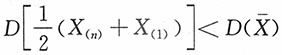
。
5. 设总体X服从
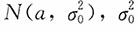
已知,X
1,X
2,…,X
n是来自总体X的一个简单随机样本,假定参数a服从N(0,1),试求a的置信水平为1-α的贝叶斯区间估计。
解:
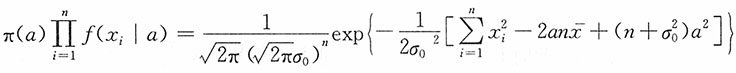
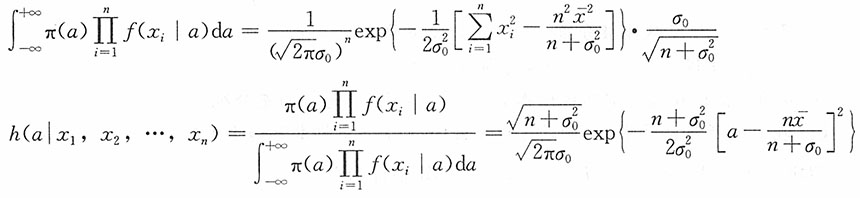
于是在给定样本X
1,X
2,…,X
n的条件下,参数a的后验分布函数为
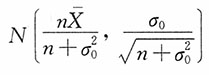
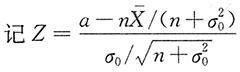
,则Z服从N(0,1),且有

贝叶斯置信区间的中心是a的贝叶斯估计
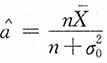
,区间长度
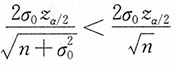
,由此,贝叶斯区间估计的精度比经典的区间估计要高。
6. 设离散总体X的分布如表所示。其中θ,0<θ<0.5是未知参数,利用总体的如下样本值:3,1,3,0,3,1,2,3,求参数θ的矩估计值和极大似然估计。
| X的分布列 |
| X | 0 | 1 | 2 | 3 |
| P | θ2 | 2θ(1-θ) | θ2 | 1-2θ |
解:(1)EX=0·θ
2+1·2θ(1-θ)+2·θ
2+3·(1-2θ)=3-4θ
又
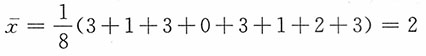
由矩估计思想建立方程3-4θ=2,从中解得参数θ的矩估计为
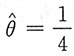
。
(2)似然函数(其中,C
+为正常数)为
L(θ)=P(X
1=x
1,X
2=x
2,…,X
8=x
8)=C
+P(X
1=3,X
2=1,…,X
8=3)
=C
+θ
2·[2θ(1-θ)]
2·θ
2·(1-2θ)
4=C
+4θ
6+(1-θ)
2(1-2θ)
4 lnL(θ)=lnC
++ln4+6lnθ+2ln(1-θ)+4ln(1-2θ),
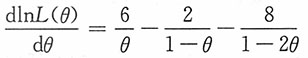
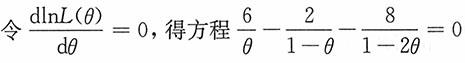
,从中解得
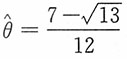
(另一根大于0.5)。
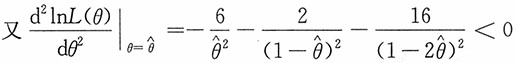
,于是参数θ的极大似然估计为
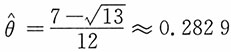
。
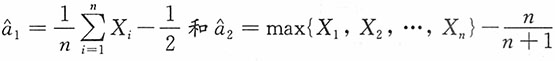 。
。8. 试比较
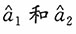
的有效性。
解:易见,当n=1时,
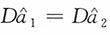
。
当n>1时,令函数g(x)=x
2-7x-2,x>1,易见g(1)=-8;且当1<x<3.5时,g(x)严格单调下降;当x>3.5时,g(x)严格单调增加。记
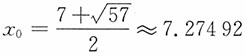
,即有g(x
0)=0进而,当1<x<x
0时,g(x)<0,(x-1)g(x)<0,即x
3-8x
2+5x+2<0,也即12x
2>x
3+4x
2+5x+2,
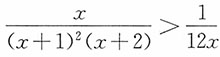
;当x>x
0时,g(x)>0,(x-1)g(x)>0,即x
3-8x
2+5x+2>0,也即12x
2<x
3+4x
2+5x+2,
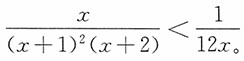
由此,当2≤n≤7时,
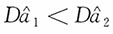
;当n≥8时,
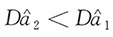
。
注 将此题作稍许改动:(1)求参数a的矩估计
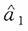
。(2)求参数a的极大似然估计。(3)记
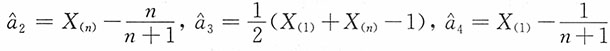
,证明
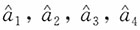
都是参数a的无偏估计,并指出哪个估计较优?
由于
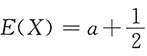
,由矩估计思想列方程
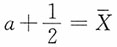
,即参数a的矩估计为
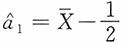
。
又似然函数为L(a)=1,a≤x
1,x
2,…,x
n≤a+1,也即L(a)=1,a≤x
(1),x
(2),…,x
(n)≤a+1,由此满足[X
(n)-1,X
(1)]中的任何值都可以作为参数a的极大似然估计。易见
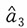
也为参数a的极大似然估计。
再者
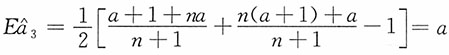
,即
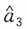
为参数a的无偏估计。
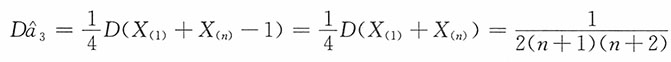

,即
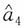
为参数a的无偏估计。

当n=1,2时,
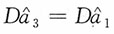
;当n≥3时,

。
当n=1时,
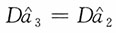
;当n≥2时,
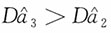
。
综上,当n=1时,
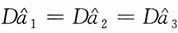
;当n=2时,
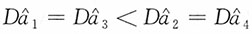
;当3≤n≤7时,
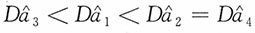
;当n≥8时,
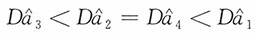
。即
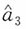
作为参数a的无偏估计较优。
9. 设总体X具有概率密度函数
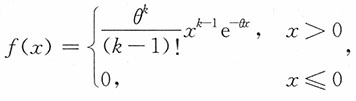
其中k为已知正整数。从该总体中随机地抽取一简单随机样本X
1,X
2,…,X
n,求θ的极大似然估计,并问这个估计量是否为无偏估计量?
解:
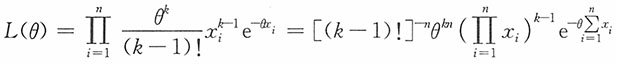

由于X~Γ(k,θ),则
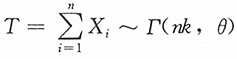
,其密度函数为
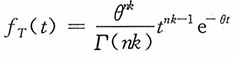
,
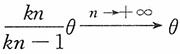
,即
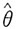
不是θ的无偏估计,而是近似无偏估计。
10. 设(X
1,Y
1),(X
2,Y
2),…,(X
n,Y
n)是取自二维正态总体
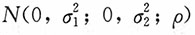
的一个简单随机样本,求
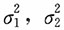
,ρ的极大似然估计。
解:
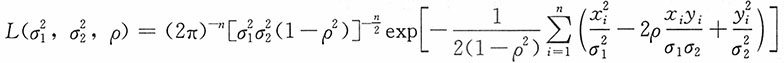
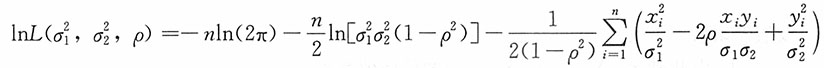
分别对
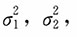
,ρ求导,并令其为0,得如下方程组
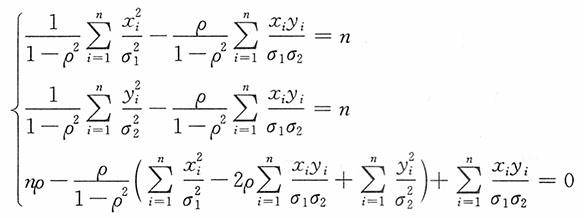
将上述第一、二方程式代人第三个方程式得
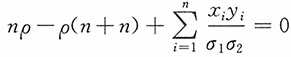
,化简得
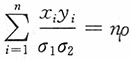
,并将其代入第一、第二个方程式得
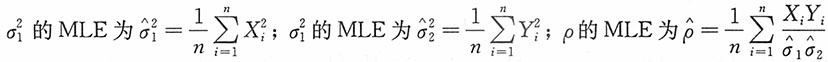
。
另解 易知,
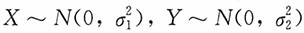
,且X,Y的相关系数为ρ,于是X
1,X
2,…,X
n为来自正态总体
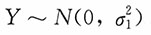
的一个简单随机样本,Y
1,Y
2,…,Y
n为来自正态总体Y~N(0,σ
2)的一个简单随机样本,参数
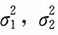
的MLE为
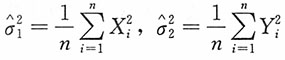
。又由上述第一个方程式可得参数ρ的MLE为
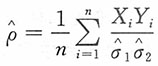
。
11. 设总体X的密度函数为
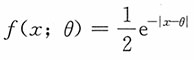
,-∞<θ<+∞,-∞<x<+∞,而X
1,X
2,…,X
n是来自总体X的一个简单随机样本,求参数θ的极大似然估计。
解:似然函数为
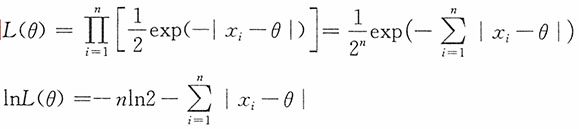
记样本观察值x
1,x
2,…,x
n中不大于θ的有k个,即有
x
(1)≤x
(2)≤…≤x
(k)≤θ<x
(k+1)≤x
(k+2)≤…≤x
(n) 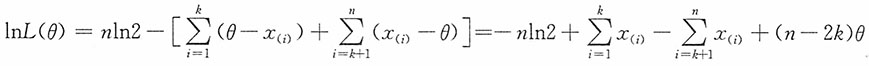
由此得θ的极大似然估计为样本的中位数,即
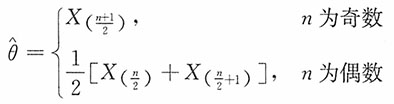
12. 若μ已知,试适当选择k,使
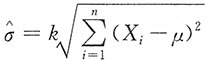
为σ的无偏估计,并求其方差。
13. 若μ未知,试适当选择k,使
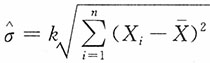
为σ的无偏估计,并求其方差。
14. 若μ已知,试适当选择k,使
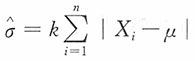
为σ的无偏估计,并求其方差。
解:注意到
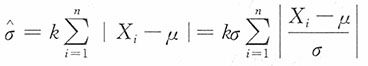
当i=1,2,…,n时,X
i~N(μ,σ
2),
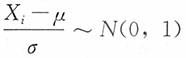

15. 若μ未知,试适当选择k,使
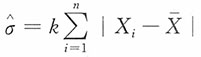
为σ的无偏估计。
16. 设总体X服从[θ-λ,θ+λ]上的均匀分布,即X~U[θ-λ,θ+λ],-∞<θ<+∞,λ>0,而X
1,X
2,…,X
n为来自总体X的容量为n的一个简单随机样本。求
(1)参数θ,λ的矩估计

,并计算其数学期望与方差。
(2)参数θ,λ的极大似然估计
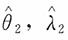
,并计算其数学期望与方差。
(3)将参数λ的极大似然估计
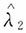
作修正,记为λ
3,使
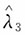
为λ的无偏估计,并求其方差。
(4)θ的矩估计与极大似然估计,哪个更有效?
解:易知E(X)=θ,
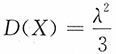
,下面求参数θ,λ的矩估计与极大似然估计。
(1)由矩估计思想可建立方程组
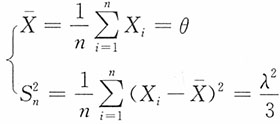
,则
参数θ,λ的矩估计分别为
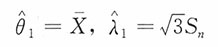
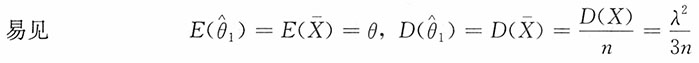
(2)似然函数为
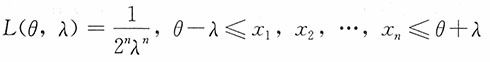
则参数θ,λ的极大似然估计
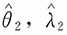
满足
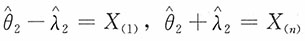
,即
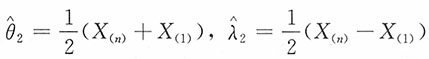
容易计算得
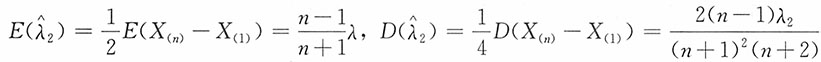
(3)
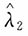
不是参数λ的无偏估计,将其进行修偏,即
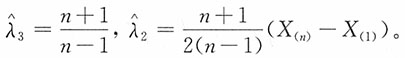
此时,其方差为
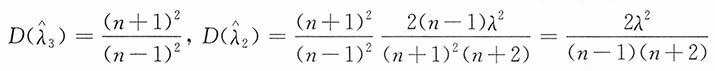
(4)关于
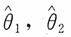
的比较:当n=2时,
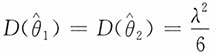
;而当n≥3时,
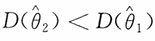
,即
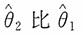
更有效。
17. 设总体X的密度函数为
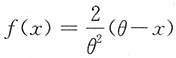
,0<x<θ,θ是未知参数。假定X
1是总体X的一个样本容量为1的简单随机样本,试求θ的置信水平为1-α的置信区间。
解:
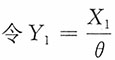
,易知Y
1的密度函数f
Y1(y),f
Y1(y)与分布函数分别为
f
Y1(y)=2(1-y),F
Y1(y)=2y-y
2,0<y<1
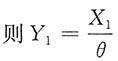
为一枢轴量,且对θ单调下降。
对给定置信水平1-α,
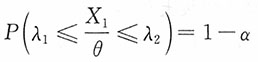
其中,λ
1,λ
2满足
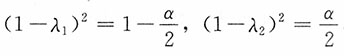
,即
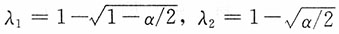
,于是有
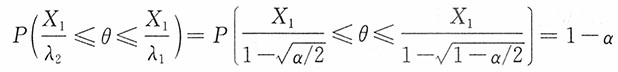
所以,θ的置信水平为1-α的置信区间为
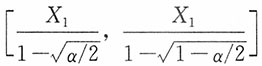
。
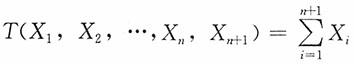 为统计量,
为统计量,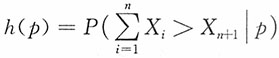 为前n个样本之和大于第n+1个样本的概率,从而h(p)为p的函数。
为前n个样本之和大于第n+1个样本的概率,从而h(p)为p的函数。18. 证明:
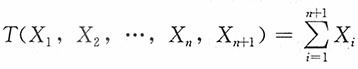
是参数p的充分统计量。
证明:(X
1,X
2,…,X
n,X
n+1)的联合分布列为
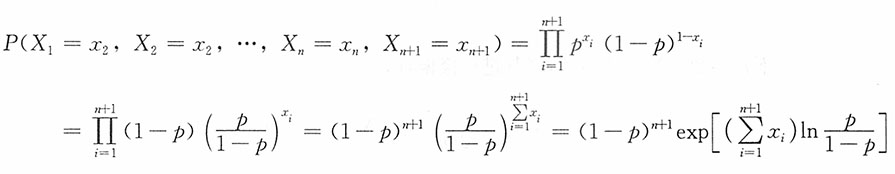
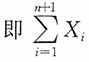
为充分完备统计量。
20. 寻找h(p)的最小方差无偏估计(需要写出具体形式)。
证明:
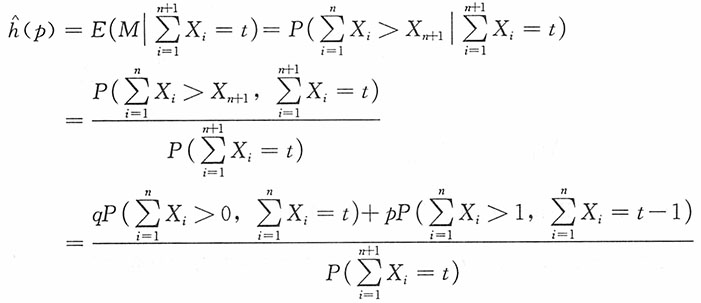
显然,若t=0是不合适的。
若t=1,则
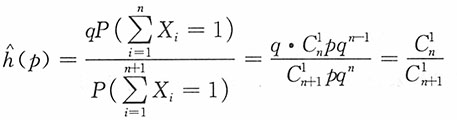
若t=2,则
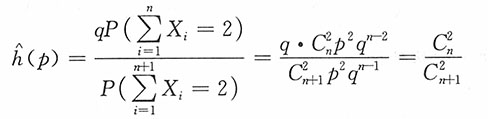
若t≥3,则
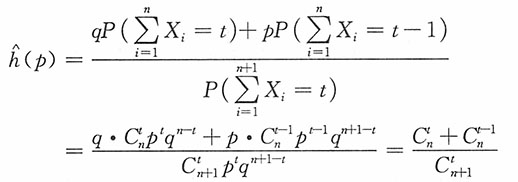
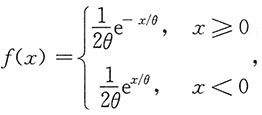 而X1,X2,…,Xn为来自总体X的一个容量为n的样本。
而X1,X2,…,Xn为来自总体X的一个容量为n的样本。21. 可否利用样本的一阶矩
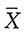
求参数θ的矩估计,为什么?
解:由于总体X服从对称拉普拉斯分布,其数学期望E(X)=0,不含未知参数θ,所以无法建立样本一阶矩等于总体一阶矩的方程。
22. 利用样本的二阶矩
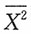
求参数θ的矩估计。
解:易见E(X
2)=2θ
2,即θ的矩估计为
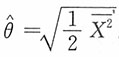
。
23. 利用样本的一阶绝对矩
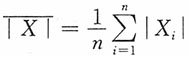
求参数θ的矩估计。
解:易见E(|X|)=θ,即θ的矩估计为
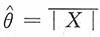
。
24. 求参数θ的极大似然估计,并求其期望与方差。
解:由于X~L(θ),其密度函数可表示为
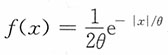
,此时似然函数为
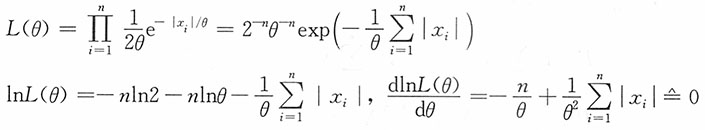
即参数θ的极大似然估计为
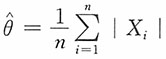
。
又由于|X|~Exp(1/θ),则
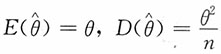
。
25. 设总体X服从参数为θ
1>0,θ
2>0的两参数非对称拉普拉斯分布,即x~L(θ
1,θ
2),其密度函数为
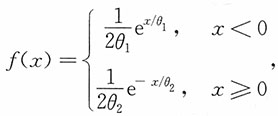
而X
1,X
2,…,X
n为来自总体X的一个容量为n的样本。(1)利用样本的一阶矩
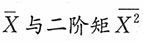
,求参数θ
1,θ
2的矩估计。(2)利用样本的一阶矩
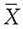
与一阶绝对矩
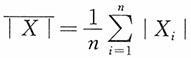
,求参数θ
1,θ
2的矩估计,并求其方差与协方差。(3)求参数θ
1,θ
2的极大似然估计。
解:

(1)由矩估计思想建立方程
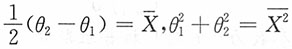
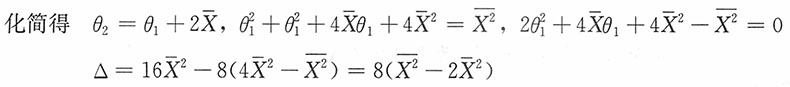
对样本附加条件一,即
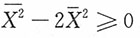
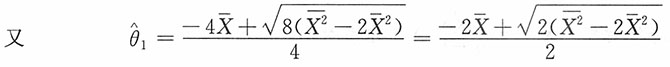
对样本附加条件二,即
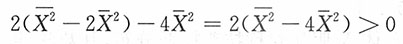
综合附加条件一与附加条件二,即要求样本满足
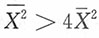
,此时参数θ
1,θ
2的矩估计为
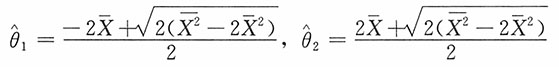
(2)由矩估计思想建立方程
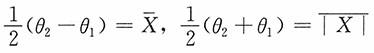
此时参数θ
1,θ
2的矩估计为

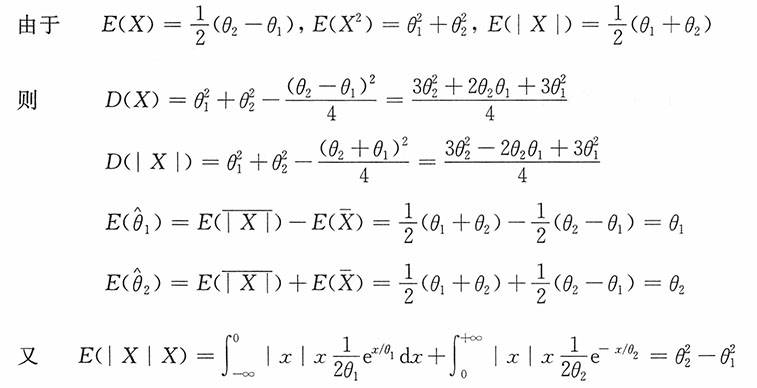
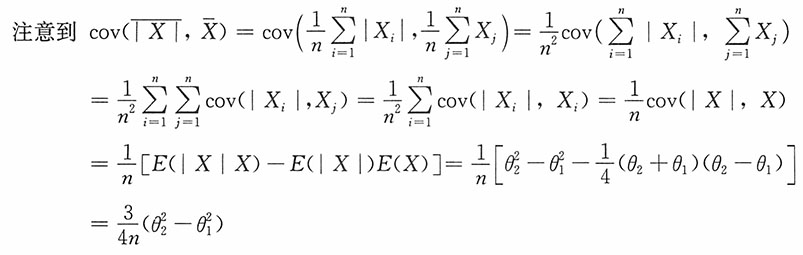
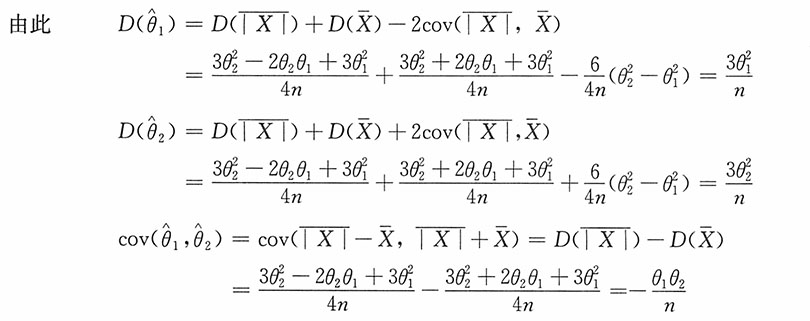
(3)将样本x
1,x
2,…,x
n从小到大排序,其中前r个小于0,后n-r个大于等于0,即
x
(1)≤x
(2)≤…≤x
(r)<0≤x
(r+1)≤…≤x
(n) 此时似然函数(其中C
+为正常数)为
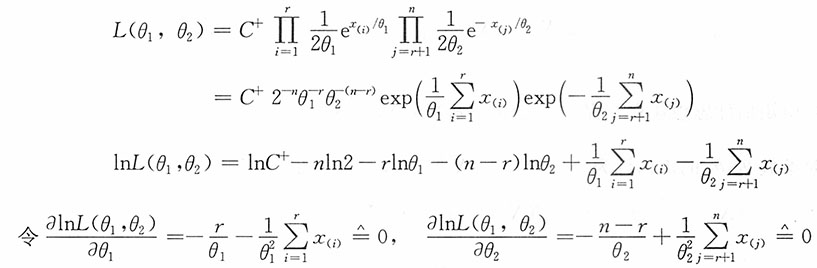
即得参数θ
1,θ
2的极大似然估计为
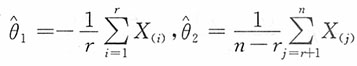
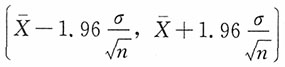 是最短的。
是最短的。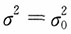 已知时,利用枢轴量
已知时,利用枢轴量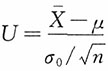 求得的均值μ的区间估计中的最短区间估计为
求得的均值μ的区间估计中的最短区间估计为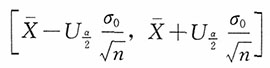
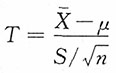 求得的均值μ的区间估计中的最短区间估计为
求得的均值μ的区间估计中的最短区间估计为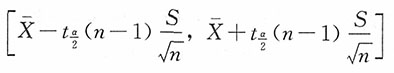
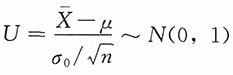 ,选取a,b,a<b,使
,选取a,b,a<b,使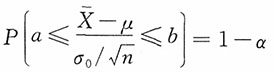
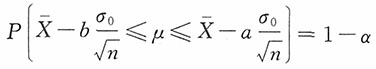
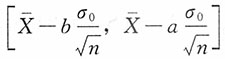 ,而此区间的平均长度为
,而此区间的平均长度为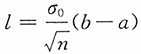 ,选取a,b,使L达到最小。
,选取a,b,使L达到最小。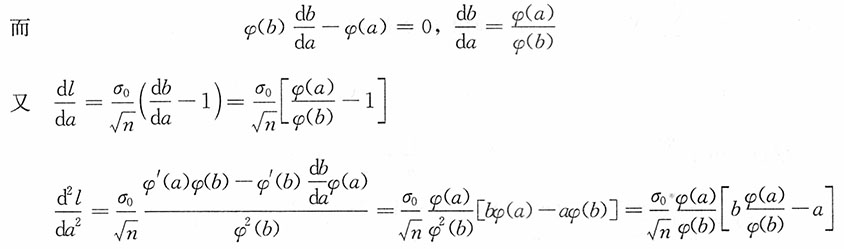
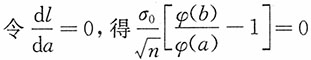 ,从中解得φ(a)=φ(b)。考虑到N(0,1)的密度函数单峰且y轴对称,又a<b,则a<b,b>0,b=-a。
,从中解得φ(a)=φ(b)。考虑到N(0,1)的密度函数单峰且y轴对称,又a<b,则a<b,b>0,b=-a。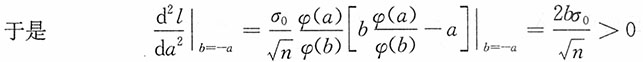
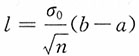 取极小值。进而可得
取极小值。进而可得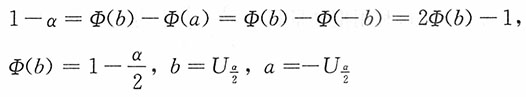
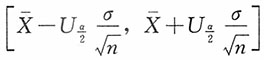 。
。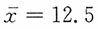 ,s=2.2,则儿童每周平均看电视时间的95%的置信区间为
,s=2.2,则儿童每周平均看电视时间的95%的置信区间为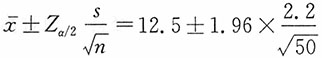 ,即12.5±0.61=(11.9,13.1),即11.9~13.1小时。
,即12.5±0.61=(11.9,13.1),即11.9~13.1小时。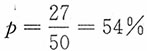 ,用样本比例p来代替总体比例π,则总体比例的置信区间可表示为
,用样本比例p来代替总体比例π,则总体比例的置信区间可表示为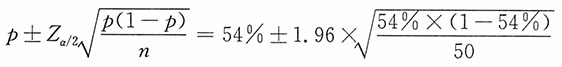
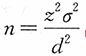 ,总体方差未知,用样本方差代替,即为
,总体方差未知,用样本方差代替,即为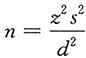 。若d缩小为原来的一半,则n扩大为原来的4倍,即为200个。
。若d缩小为原来的一半,则n扩大为原来的4倍,即为200个。 -∞<θ<+∞,X1,X2,…,Xn为其子样。
-∞<θ<+∞,X1,X2,…,Xn为其子样。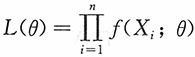 。易见当
。易见当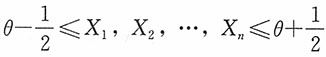 时,L(θ)取到最大值1,此时
时,L(θ)取到最大值1,此时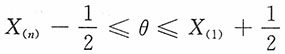 ,于是参数θ的极大似然估计为
,于是参数θ的极大似然估计为 中的任何值。
中的任何值。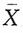 及
及 都是θ的无偏估计量,问哪个较有效?
都是θ的无偏估计量,问哪个较有效?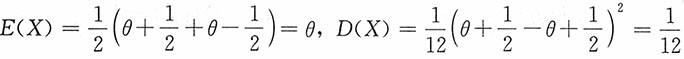 ,则
,则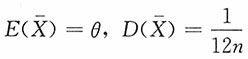
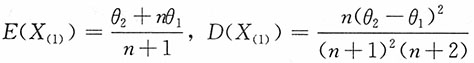
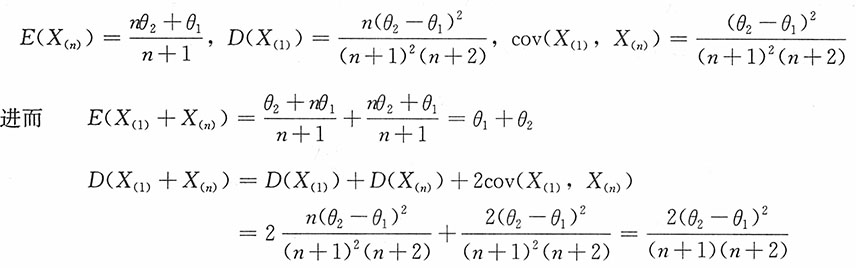
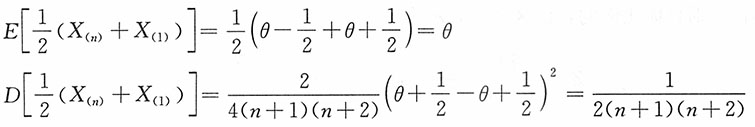
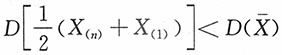 。
。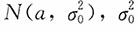 已知,X1,X2,…,Xn是来自总体X的一个简单随机样本,假定参数a服从N(0,1),试求a的置信水平为1-α的贝叶斯区间估计。
已知,X1,X2,…,Xn是来自总体X的一个简单随机样本,假定参数a服从N(0,1),试求a的置信水平为1-α的贝叶斯区间估计。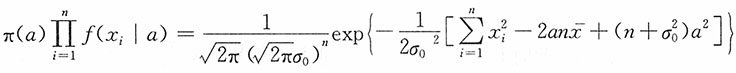
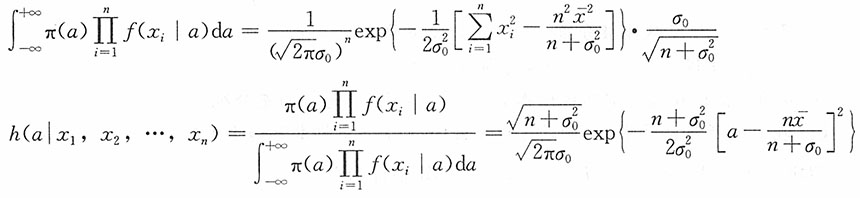
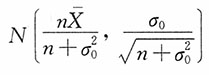
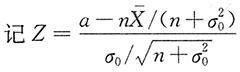 ,则Z服从N(0,1),且有
,则Z服从N(0,1),且有
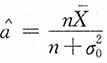 ,区间长度
,区间长度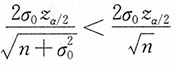 ,由此,贝叶斯区间估计的精度比经典的区间估计要高。
,由此,贝叶斯区间估计的精度比经典的区间估计要高。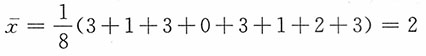
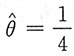 。
。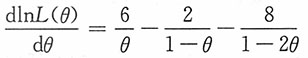
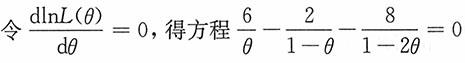 ,从中解得
,从中解得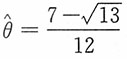 (另一根大于0.5)。
(另一根大于0.5)。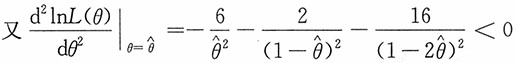 ,于是参数θ的极大似然估计为
,于是参数θ的极大似然估计为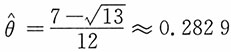 。
。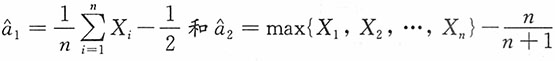 。
。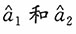 都是a的无偏估计。
都是a的无偏估计。
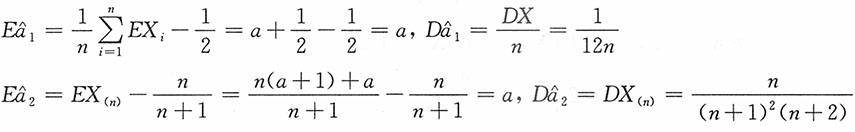
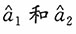 的有效性。
的有效性。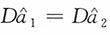 。
。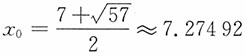 ,即有g(x0)=0进而,当1<x<x0时,g(x)<0,(x-1)g(x)<0,即x3-8x2+5x+2<0,也即12x2>x3+4x2+5x+2,
,即有g(x0)=0进而,当1<x<x0时,g(x)<0,(x-1)g(x)<0,即x3-8x2+5x+2<0,也即12x2>x3+4x2+5x+2,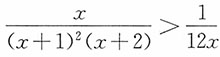 ;当x>x0时,g(x)>0,(x-1)g(x)>0,即x3-8x2+5x+2>0,也即12x2<x3+4x2+5x+2,
;当x>x0时,g(x)>0,(x-1)g(x)>0,即x3-8x2+5x+2>0,也即12x2<x3+4x2+5x+2,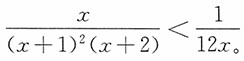
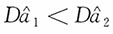 ;当n≥8时,
;当n≥8时,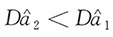 。
。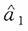 。(2)求参数a的极大似然估计。(3)记
。(2)求参数a的极大似然估计。(3)记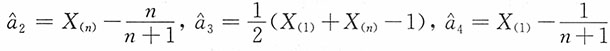 ,证明
,证明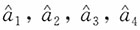 都是参数a的无偏估计,并指出哪个估计较优?
都是参数a的无偏估计,并指出哪个估计较优?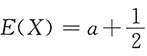 ,由矩估计思想列方程
,由矩估计思想列方程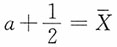 ,即参数a的矩估计为
,即参数a的矩估计为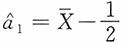 。
。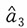 也为参数a的极大似然估计。
也为参数a的极大似然估计。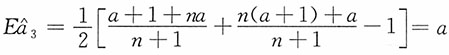 ,即
,即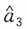 为参数a的无偏估计。
为参数a的无偏估计。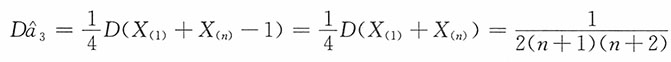
 ,即
,即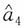 为参数a的无偏估计。
为参数a的无偏估计。
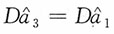 ;当n≥3时,
;当n≥3时, 。
。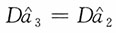 ;当n≥2时,
;当n≥2时,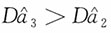 。
。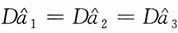 ;当n=2时,
;当n=2时,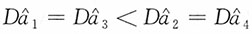 ;当3≤n≤7时,
;当3≤n≤7时,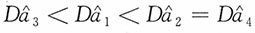 ;当n≥8时,
;当n≥8时,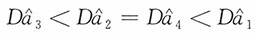 。即
。即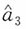 作为参数a的无偏估计较优。
作为参数a的无偏估计较优。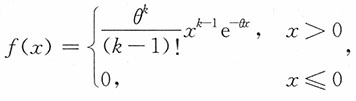 其中k为已知正整数。从该总体中随机地抽取一简单随机样本X1,X2,…,Xn,求θ的极大似然估计,并问这个估计量是否为无偏估计量?
其中k为已知正整数。从该总体中随机地抽取一简单随机样本X1,X2,…,Xn,求θ的极大似然估计,并问这个估计量是否为无偏估计量?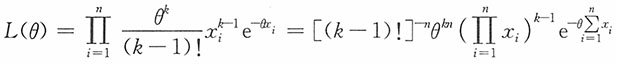

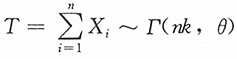 ,其密度函数为
,其密度函数为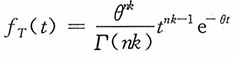 ,
,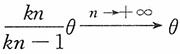 ,即
,即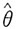 不是θ的无偏估计,而是近似无偏估计。
不是θ的无偏估计,而是近似无偏估计。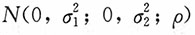 的一个简单随机样本,求
的一个简单随机样本,求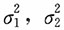 ,ρ的极大似然估计。
,ρ的极大似然估计。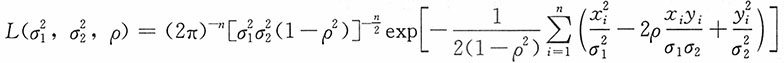
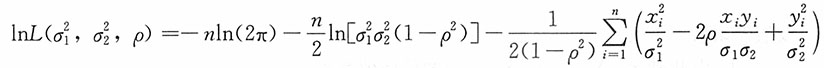
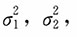 ,ρ求导,并令其为0,得如下方程组
,ρ求导,并令其为0,得如下方程组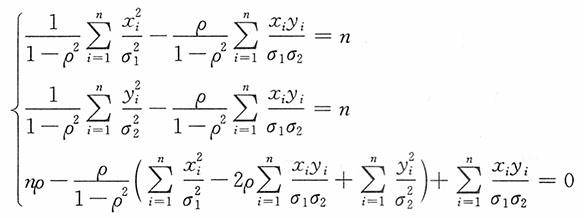
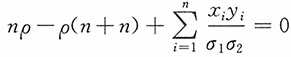 ,化简得
,化简得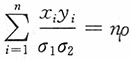 ,并将其代入第一、第二个方程式得
,并将其代入第一、第二个方程式得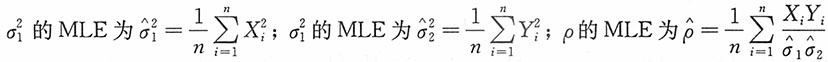 。
。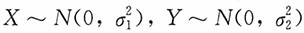 ,且X,Y的相关系数为ρ,于是X1,X2,…,Xn为来自正态总体
,且X,Y的相关系数为ρ,于是X1,X2,…,Xn为来自正态总体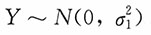 的一个简单随机样本,Y1,Y2,…,Yn为来自正态总体Y~N(0,σ2)的一个简单随机样本,参数
的一个简单随机样本,Y1,Y2,…,Yn为来自正态总体Y~N(0,σ2)的一个简单随机样本,参数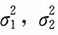 的MLE为
的MLE为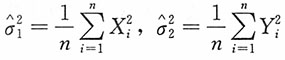 。又由上述第一个方程式可得参数ρ的MLE为
。又由上述第一个方程式可得参数ρ的MLE为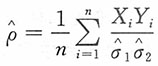 。
。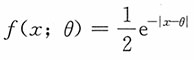 ,-∞<θ<+∞,-∞<x<+∞,而X1,X2,…,Xn是来自总体X的一个简单随机样本,求参数θ的极大似然估计。
,-∞<θ<+∞,-∞<x<+∞,而X1,X2,…,Xn是来自总体X的一个简单随机样本,求参数θ的极大似然估计。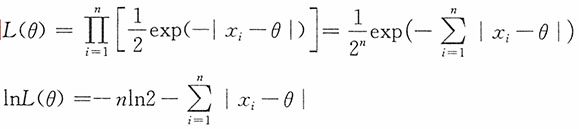
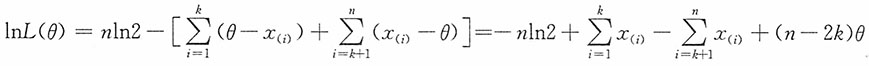
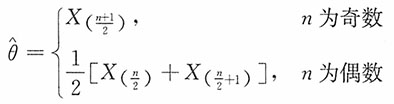
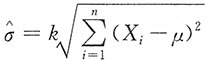 为σ的无偏估计,并求其方差。
为σ的无偏估计,并求其方差。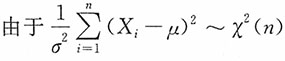 ,所以
,所以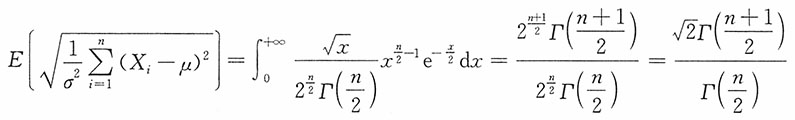
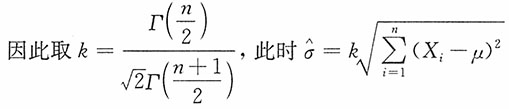 为σ的无偏估计。求其方差
为σ的无偏估计。求其方差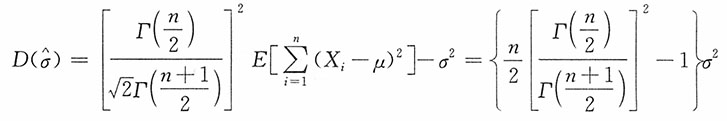
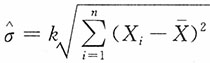 为σ的无偏估计,并求其方差。
为σ的无偏估计,并求其方差。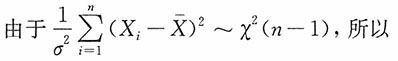
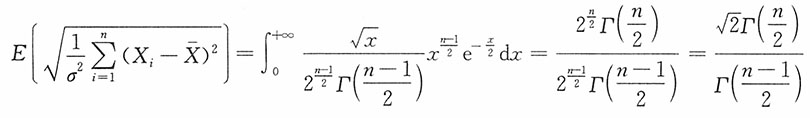
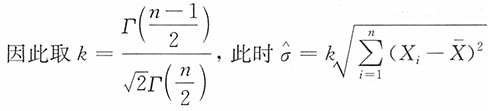 为σ的无偏估计。求其方差
为σ的无偏估计。求其方差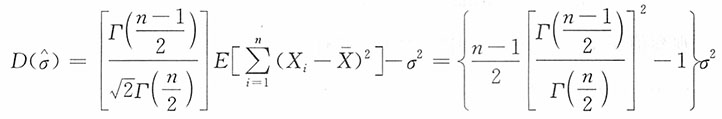
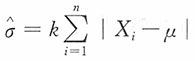 为σ的无偏估计,并求其方差。
为σ的无偏估计,并求其方差。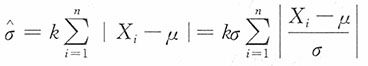
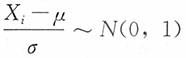

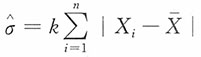 为σ的无偏估计。
为σ的无偏估计。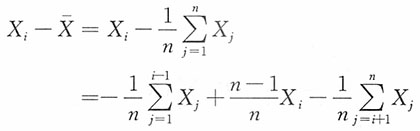
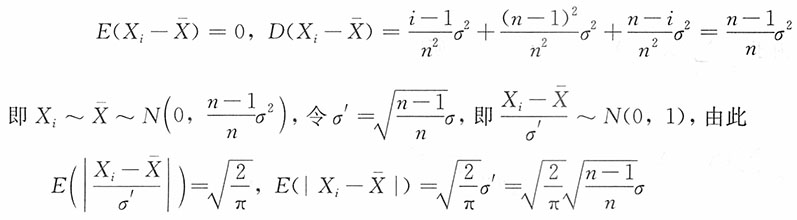
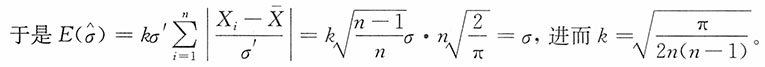
 ,并计算其数学期望与方差。
,并计算其数学期望与方差。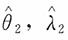 ,并计算其数学期望与方差。
,并计算其数学期望与方差。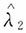 作修正,记为λ3,使
作修正,记为λ3,使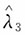 为λ的无偏估计,并求其方差。
为λ的无偏估计,并求其方差。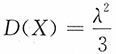 ,下面求参数θ,λ的矩估计与极大似然估计。
,下面求参数θ,λ的矩估计与极大似然估计。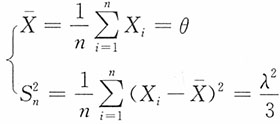 ,则
,则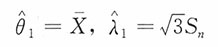
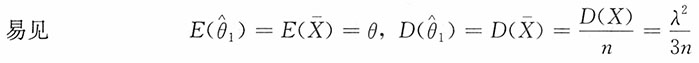
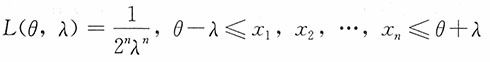
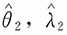 满足
满足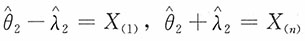 ,即
,即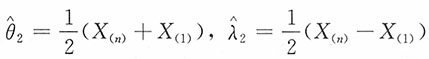
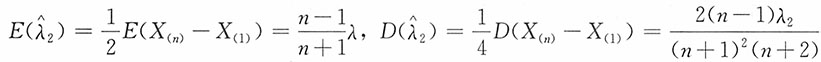
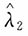 不是参数λ的无偏估计,将其进行修偏,即
不是参数λ的无偏估计,将其进行修偏,即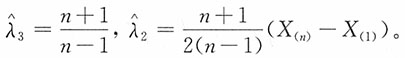
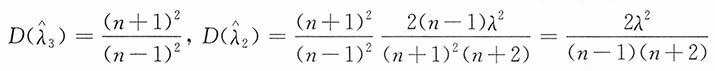
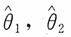 的比较:当n=2时,
的比较:当n=2时,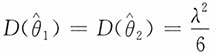 ;而当n≥3时,
;而当n≥3时,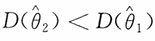 ,即
,即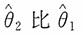 更有效。
更有效。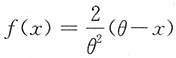 ,0<x<θ,θ是未知参数。假定X1是总体X的一个样本容量为1的简单随机样本,试求θ的置信水平为1-α的置信区间。
,0<x<θ,θ是未知参数。假定X1是总体X的一个样本容量为1的简单随机样本,试求θ的置信水平为1-α的置信区间。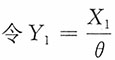 ,易知Y1的密度函数fY1(y),fY1(y)与分布函数分别为
,易知Y1的密度函数fY1(y),fY1(y)与分布函数分别为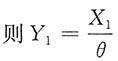 为一枢轴量,且对θ单调下降。
为一枢轴量,且对θ单调下降。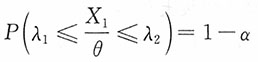
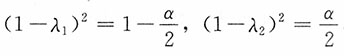 ,即
,即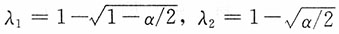 ,于是有
,于是有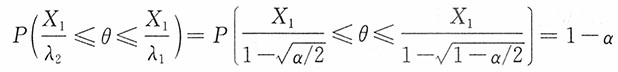
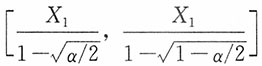 。
。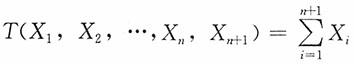 为统计量,
为统计量,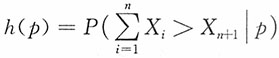 为前n个样本之和大于第n+1个样本的概率,从而h(p)为p的函数。
为前n个样本之和大于第n+1个样本的概率,从而h(p)为p的函数。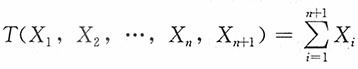 是参数p的充分统计量。
是参数p的充分统计量。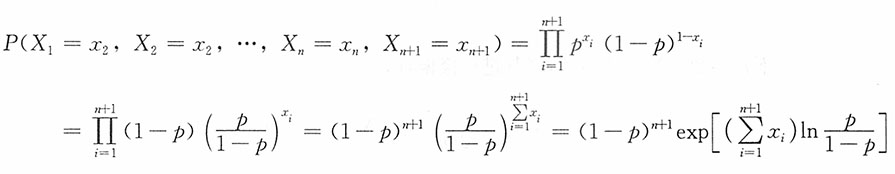
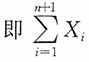 为充分完备统计量。
为充分完备统计量。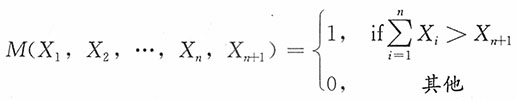 是h(p)的无偏估计量。
是h(p)的无偏估计量。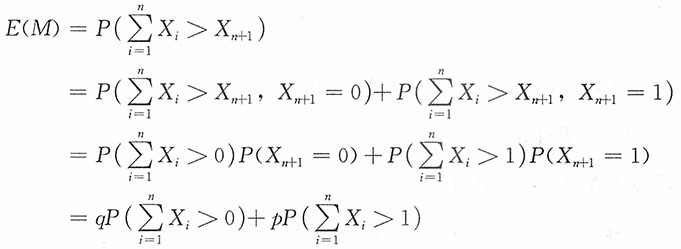
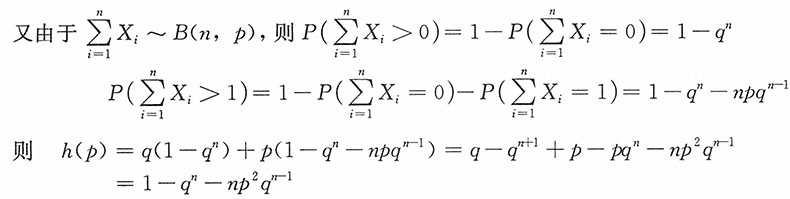
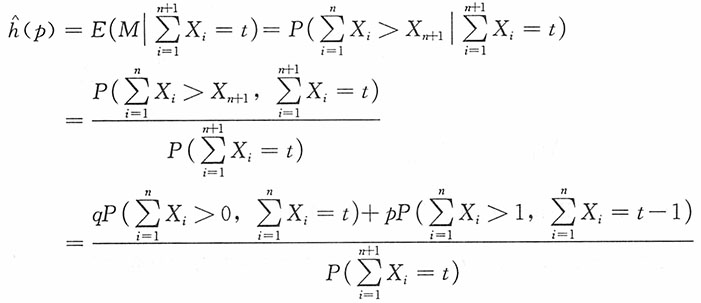
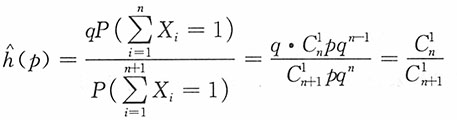
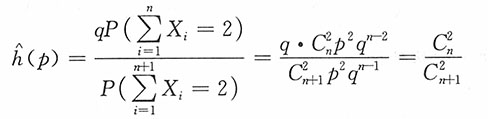
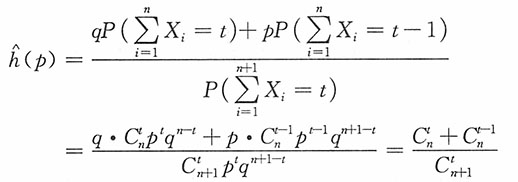
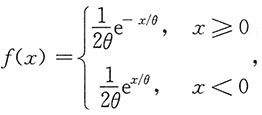 而X1,X2,…,Xn为来自总体X的一个容量为n的样本。
而X1,X2,…,Xn为来自总体X的一个容量为n的样本。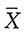 求参数θ的矩估计,为什么?
求参数θ的矩估计,为什么?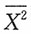 求参数θ的矩估计。
求参数θ的矩估计。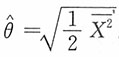 。
。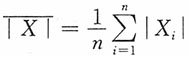 求参数θ的矩估计。
求参数θ的矩估计。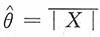 。
。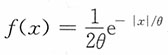 ,此时似然函数为
,此时似然函数为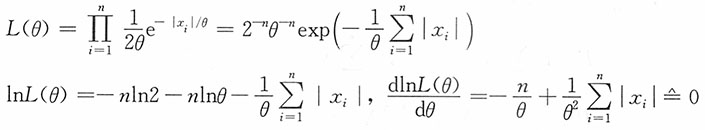
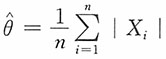 。
。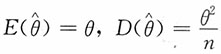 。
。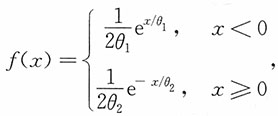 而X1,X2,…,Xn为来自总体X的一个容量为n的样本。(1)利用样本的一阶矩
而X1,X2,…,Xn为来自总体X的一个容量为n的样本。(1)利用样本的一阶矩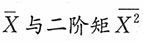 ,求参数θ1,θ2的矩估计。(2)利用样本的一阶矩
,求参数θ1,θ2的矩估计。(2)利用样本的一阶矩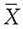 与一阶绝对矩
与一阶绝对矩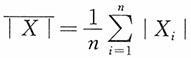 ,求参数θ1,θ2的矩估计,并求其方差与协方差。(3)求参数θ1,θ2的极大似然估计。
,求参数θ1,θ2的矩估计,并求其方差与协方差。(3)求参数θ1,θ2的极大似然估计。
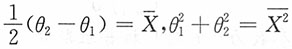
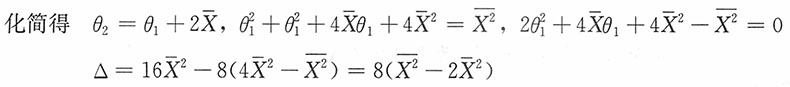
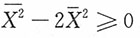
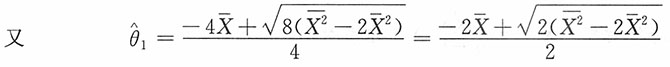
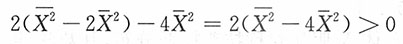
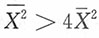 ,此时参数θ1,θ2的矩估计为
,此时参数θ1,θ2的矩估计为