第Ⅰ卷(选择题)
一、选择题在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若D为x
2+y
2≤4所确定的区域,则
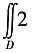
·dσ=______.
A B C D
D
[解析] 区域D为一个圆域,且其面积S=4π.
由二重积分的性质可得
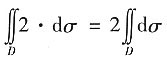
=2·S=8π.
5. 若
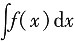
=xln(x+1)+C,则
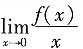
等于______.
A B C D
A
[考点] 本题考查一元函数的导数及其极限.
[解析] 因为
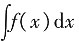
=xln(x+1)+C,所以f(x)=[xln(x+1)+C]'=ln(x+1)+
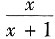
,故
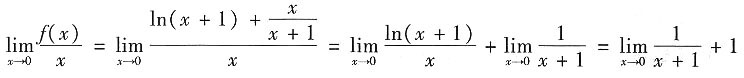
=2.
7. 函数y=x
2-x+1在区间[-1,3]上满足拉格朗日中值定理的ξ等于______.
A.
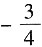
B.0
C.
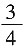
D.1
A B C D
D
[解析] 由于函数y=x2-x+1在区间[-1,3]上连续,在区间(-1,3)内可导,因此在[-1,3]上,y满足拉格朗日中值定理条件.又y'=2x-1,则存在ξ∈(-1,3),使得
f(3)-f(-1)=(2ξ-1)[3-(-1)],
即4(2ξ-1)=7-3,解得ξ=1.
第Ⅱ卷(非选择题)
二、填空题1. 过原点且与直线
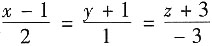
垂直的平面方程为______.
2x+y-3z=0
[考点] 本题考查平面方程和平面与直线的关系.
[解析] 由于已知直线与所求平面垂直,可知所给直线的方向向量s平行于所求平面的法向量n.
由于s=(2,1,-3),因此可取n=(2,1,-3).由于平面过原点,由平面的点法式方程,可知所求平面方程为2x+y-3z=0.
2. 设y=-f(x)是由方程x
3-y
3-3xy-9=0所确定的隐函数,则y'=______.
[解析] 解法一 将方程两端对x求导,可得3x
2-3y
2y'-3y-3xy'=0.
整理得 y'=
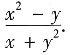
解法二 方程两端取微分,可得
d(x
3-y
3-3xy-9)=3x
2dx-3y
2dy-3(ydx+xdy)
=(3x
2-3y)dx-(3y
2+3x)dy=0.
因此 y'=
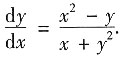
3.
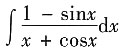
=______.
ln|x+cosx|+C
[解析] 利用凑微分法求解该不定积分,则有
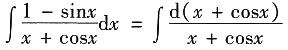
=ln|x+cosx|+C.
4. 曲线y=x
3-6x的拐点坐标为______.
(0,0)
[解析] 由y=x3-6x,得y'=3x2-6,y"=6x.令y"=0,得到x=0.
当x=0时,y=0.当x<0时,y"<0;当x>0时,y">0.
因此点(0,0)是曲线y=x3-6x的拐点.
5. 方程y'=2xy的诵解为______.
y=
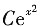
[解析] 方程y'=2xy为可分离变量微分方程,分离变量可得

=2xdx.
两边同时取积分可得lny=x
2+C
1,即通解为y=
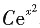
.
6. 若f'(e
x)=1+e
2x,且f(0)=1,则f(x)=______.
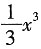
+x+1
[解析] 由f'(e
x)=1+e
2x,可知f'(x)=1+x
2.两端积分可得
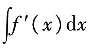
=
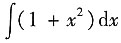
,即f(x)=

+x+C.
又f(0)=C=1.因此f(x)=
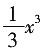
+x+1.
7. 过点(1,-1,0)且与直线
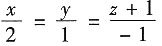
平行的直线方程为______.
[考点] 本题考查直线的方程和直线与直线的关系.
[解析] 由于两条直线平行的充分必要条件为它们的方向向量平行,因此可取所求直线的方向向量为(2,1,-1).由直线的点向式方程可知所求直线方程为
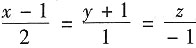
.
8. 当x=1时,f(x)=x
3+3px+q取到极值(其中q为任意常数),则p=______.
-1
[解析] f'(x)=3x2+3p,f'(1)=3+3p=0,所以p=-1.
9. 已知当x→0时,

-1与x
2是等价无穷小,则a=______.
2
[解析] 由于当x→0时,
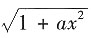
-1与x
2是等价无穷小,则
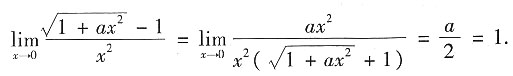
因此可得a=2.
10. 过点(1,2,-1)且与直线
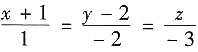
垂直的平面方程为______.
x-2y-3z=0
[解析] 由于已知直线与平面垂直,且直线的方向向量为(1,-2,-3),因此所求平面的法向量可取为(1,-2,-3).又平面过点(1,2,-1),由平面的点法式,可得平面方程为(x-1)-2(y-2)-3(z+1)=0,即x-2y-3z=0.
三、解答题共70分,解答应写出推理、演算步骤.1. 计算
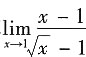
.
解法一 分母先有理化,可得
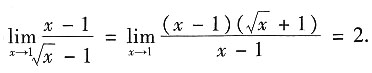
解法二 换元法.令t=

,则x=t
2,且当x→1时,t→1.因此
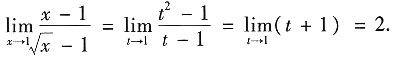
2. 计算
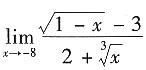
.
解法一 当x→-8时,分子分母均趋于零,所求极限符合洛必达使用条件.
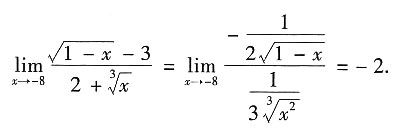
解法二 用变量替换法进行求解.
令t=
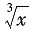
,则x=t
3,且当x→-8时,t→-2.因此
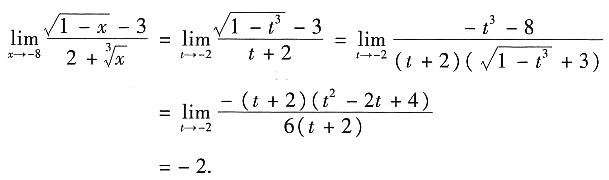
3. 计算
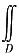
(x+y
2)dxdy,其中区域D由直线y=x,y=1与y轴围成.
由积分区域的图形特征以及被积函数的特征可知,积分区域D既可以表示成X型区域,又可以表示成Y型区域.
解法一 当积分区域看成X型区域时(即先对y积分,再对x积分),区域D可表示为
0≤x≤1, x≤y≤1.
因此
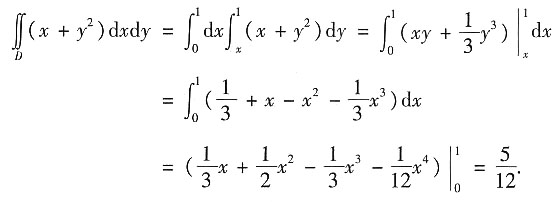
解法二 当积分区域看成Y型区域时(即先对x积分,再对y积分),区域D可表示为
0≤Y≤1,0≤x≤y.
因此
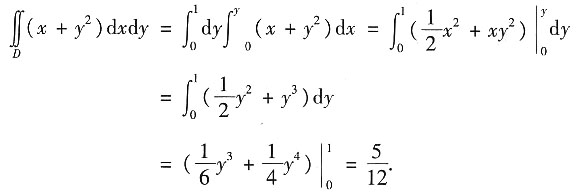
4. 计算二重积分
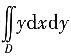
,其中D为曲线x=y
2+1,直线x=0,y=0,y=1所围成的区域.
由积分区域D的图形特征可知,把二重积分转化为先对x积分,再对y积分的二次积分更容易求解.此时积分区域D可表示为
0≤x≤y
2+1.0≤y≤1.
因此
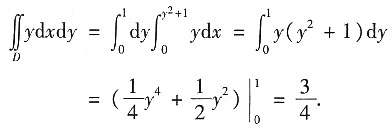
5. 设

.
本题考查形式为参数方程的函数的求导的相关知识.
由于
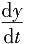
=6t
2+6t=6t(t+1),
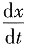
=e
t+te
t=(t+1)e
t,
因此
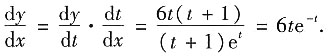
6. 求函数f(x,y)=e
2y(x
2+2x+y)的极值.
联立方程组
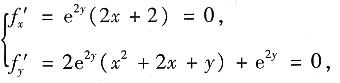
解得唯一驻点(-1,
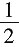
).并在该驻点处,
A=
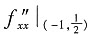
=2e,B=
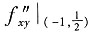
=0,C=
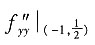
=2e.
由于AC-B
2=4e
2>0,且A>0,
因此(-1,

)为极小值点,且极小值为f(-1,
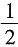
)=
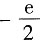
.
7. 求微分方程y"-2y'-3y=e
-2x的通解.
齐次微分方程y"-2y'-3y=0对应的特征方程是
r
2-2r-3=0.
解得特征根r
1=-1,r
2=3.
因此齐次方程的通解为Y=C
1e
-x+C
2e
3x.
原非齐次微分方程的自由项为f(x)=e
-2x,且α=-2不是特征根.
则可设y
*=Ae
-2x为原非齐次方程的一个特解,代入该方程可得
4Ae
-2x+4Ae
-2x-3Ae
-2x=e
-2x.
解得A=
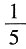
.则y
*=
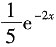
.因此原微分方程的通解为
y=Y+y
*=C
1e
-x+C
2e
3x+
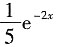
(C
1,C
2为任意常数).
8. 已知z=xy
2,y=e
t,x=t
3+t,求
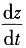
,dz.
解法一 将y=e
t,x=t
3+t代入z=xy
2,则有
z=(t
3+t)e
2t.
此时z变成关于t的一元函数.因此可得
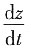
=(3t
2+1)e
2t+(t
3+t)2e
2t
=(2t
3+3t
2+2t+1)e
2t.
进而 dz=(2t
3+3t
2+2t+1)e
2tdt.
解法二 利用复合函数的求导法则求解.首先可知
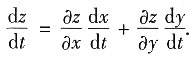
又
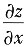
=y
2=e
2t,

=2xy=2(t
3+t)e
t.
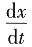
=3t
2+1,
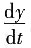
=e
t.
因此
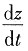
=e
2t(3t
2+1)+2(t
3+t)e
te
t
=(2t
3+3t
2+2t+1)e
2t.
进而 dz=(2t
3+3t
2+2t+1)e
2tdt.
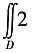 ·dσ=______.
·dσ=______.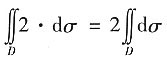 =2·S=8π.
=2·S=8π. =-1≠0,显然点(1,0)不是驻点,故其处无极值.
=-1≠0,显然点(1,0)不是驻点,故其处无极值.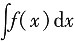 =xln(x+1)+C,则
=xln(x+1)+C,则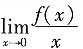 等于______.
等于______.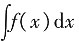 =xln(x+1)+C,所以f(x)=[xln(x+1)+C]'=ln(x+1)+
=xln(x+1)+C,所以f(x)=[xln(x+1)+C]'=ln(x+1)+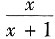 ,故
,故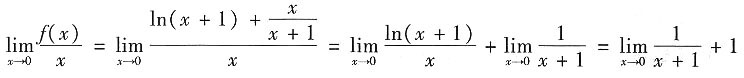 =2.
=2.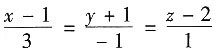 与平面x+2y-z+3=0的位置关系是______.
与平面x+2y-z+3=0的位置关系是______.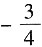
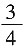
 ,则f(x)在x=0处______.
,则f(x)在x=0处______.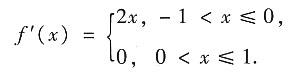
 =0=f'(0),故函数f(x)在x=0可导.
=0=f'(0),故函数f(x)在x=0可导. =-dx.
=-dx.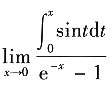 =______.
=______.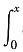 sintdt→0,且e-x-1→0.由洛必达法则,得
sintdt→0,且e-x-1→0.由洛必达法则,得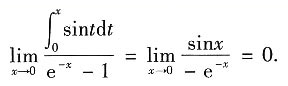
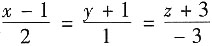 垂直的平面方程为______.
垂直的平面方程为______.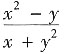
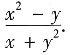
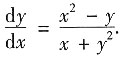
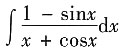 =______.
=______.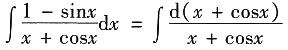 =ln|x+cosx|+C.
=ln|x+cosx|+C.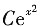
 =2xdx.
=2xdx.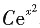 .
.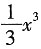 +x+1
+x+1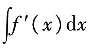 =
=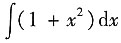 ,即f(x)=
,即f(x)= +x+C.
+x+C.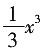 +x+1.
+x+1.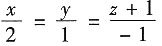 平行的直线方程为______.
平行的直线方程为______.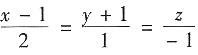
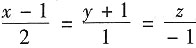 .
. -1与x2是等价无穷小,则a=______.
-1与x2是等价无穷小,则a=______.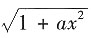 -1与x2是等价无穷小,则
-1与x2是等价无穷小,则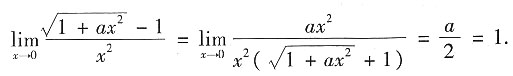
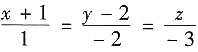 垂直的平面方程为______.
垂直的平面方程为______.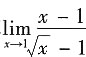 .
.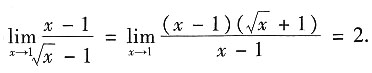
 ,则x=t2,且当x→1时,t→1.因此
,则x=t2,且当x→1时,t→1.因此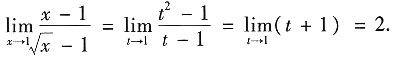
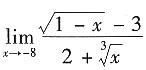 .
.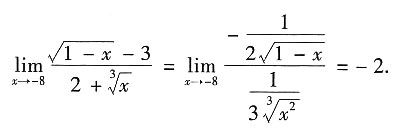
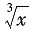 ,则x=t3,且当x→-8时,t→-2.因此
,则x=t3,且当x→-8时,t→-2.因此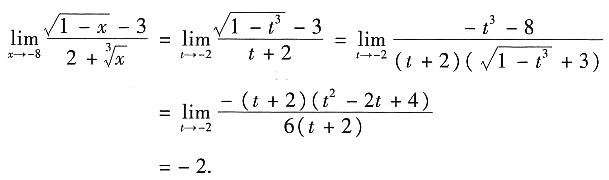
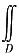 (x+y2)dxdy,其中区域D由直线y=x,y=1与y轴围成.
(x+y2)dxdy,其中区域D由直线y=x,y=1与y轴围成.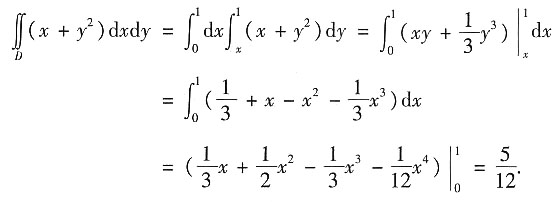
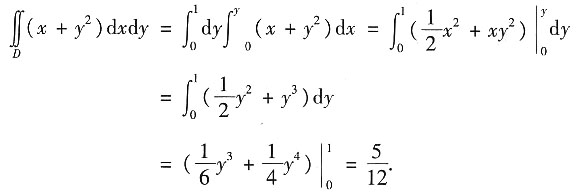
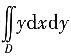 ,其中D为曲线x=y2+1,直线x=0,y=0,y=1所围成的区域.
,其中D为曲线x=y2+1,直线x=0,y=0,y=1所围成的区域.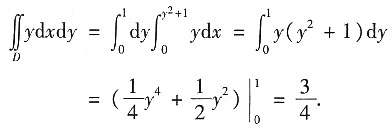
 .
.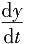 =6t2+6t=6t(t+1),
=6t2+6t=6t(t+1),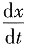 =et+tet=(t+1)et,
=et+tet=(t+1)et,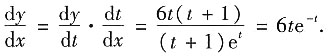
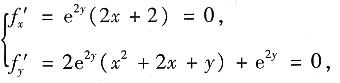
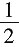 ).并在该驻点处,
).并在该驻点处,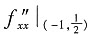 =2e,B=
=2e,B=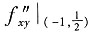 =0,C=
=0,C=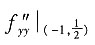 =2e.
=2e. )为极小值点,且极小值为f(-1,
)为极小值点,且极小值为f(-1,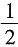 )=
)=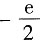 .
.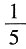 .则y*=
.则y*=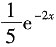 .因此原微分方程的通解为
.因此原微分方程的通解为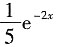 (C1,C2为任意常数).
(C1,C2为任意常数).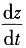 ,dz.
,dz.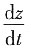 =(3t2+1)e2t+(t3+t)2e2t
=(3t2+1)e2t+(t3+t)2e2t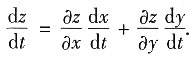
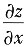 =y2=e2t,
=y2=e2t, =2xy=2(t3+t)et.
=2xy=2(t3+t)et.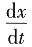 =3t2+1,
=3t2+1,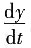 =et.
=et.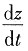 =e2t(3t2+1)+2(t3+t)etet
=e2t(3t2+1)+2(t3+t)etet