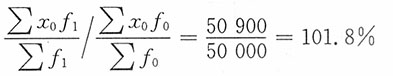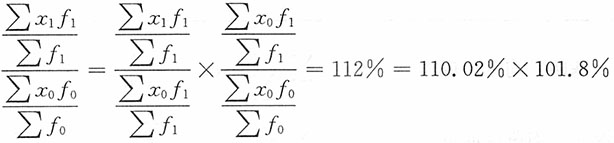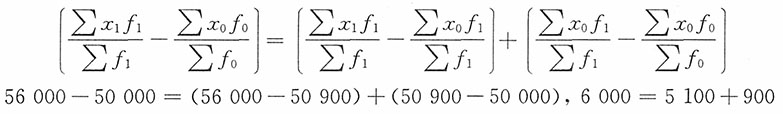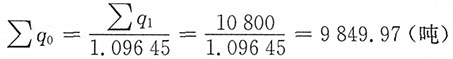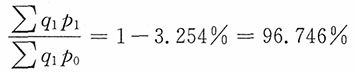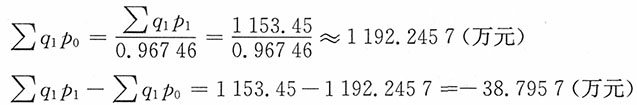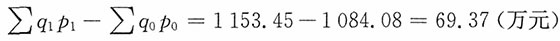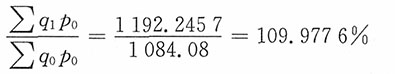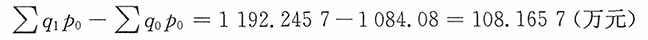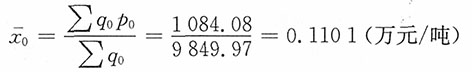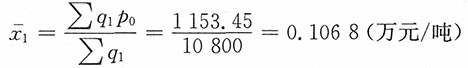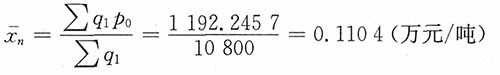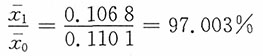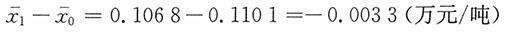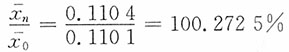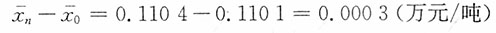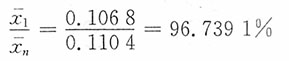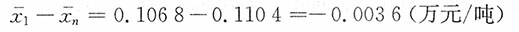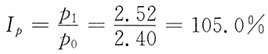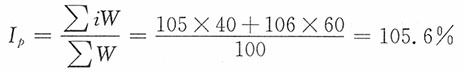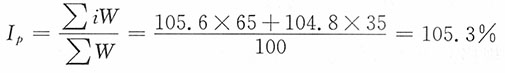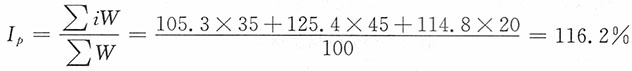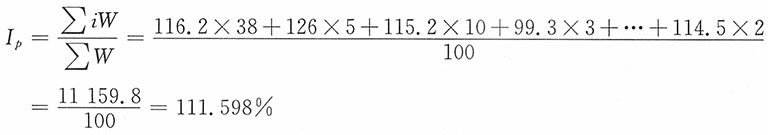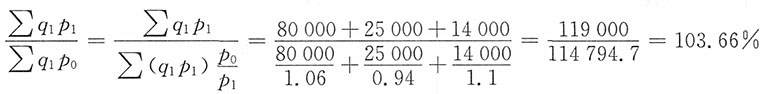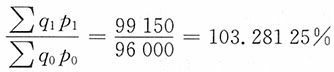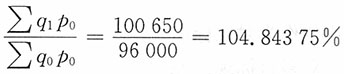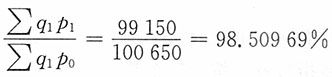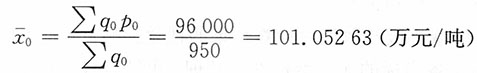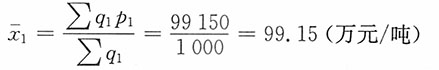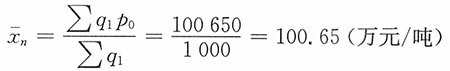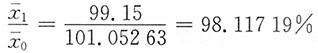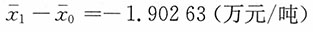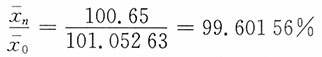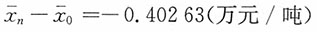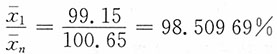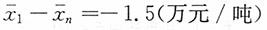计算题1. 下表是一家啤酒生产企业2010—2015年各季度的啤酒销售量数据(单位:万吨)。试绘制时间度列图,并利用移动平均趋势剔除法计算季节指数,观察啤酒销售量的构成要素。
| 2010—2015各季度的啤酒销售量 单位:万吨 |
| | A | B | C | D | E |
| 1 | 年份(年) | 季度 |
| 2 | 1 | 2 | 3 | 4 |
| 3 | 2010 | 25 | 32 | 37 | 26 |
| 4 | 2011 | 30 | 38 | 42 | 30 |
| 5 | 2012 | 29 | 39 | 50 | 35 |
| 6 | 2013 | 30 | 39 | 51 | 37 |
| 7 | 2014 | 29 | 42 | 55 | 38 |
| 8 | 2015 | 31 | 43 | 54 | 41 |
解:啤酒销售量的时间序列图如图1所示。从图1中可以看出,啤酒销售量具有明显的季节成分,而且后面年份的销售量比前面的年份高,因此其中还含有趋势成分,但其周期性难以判断。可以认定啤酒销售量序列是一个含有季节成分和趋势成分的时间序列。
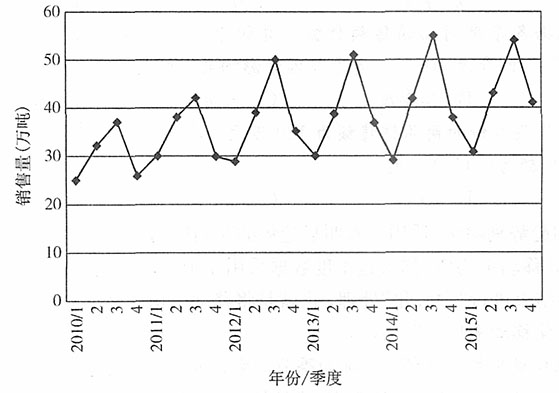 图1 啤酒销售量时间序列图
图1 啤酒销售量时间序列图 为预测啤酒销售量,首先确定季节成分,并从序列中将季节成分剔除,然后根据剔除季节成分的序列选择适当的预测模型并进行预测。
有关计算过程见下表所示。
| 表1 计算过程
|
|
|
A
|
B
|
C
|
D
|
E
|
| 1
|
年/季度
|
时间标号t
|
销售量(Y)
|
中心化移动
平均值(CMA)
|
比值(Y/CMA)
|
| 2
|
2010/1
|
1
|
25
|
—
|
—
|
| 3
|
2
|
2
|
32
|
—
|
—
|
| 4
|
3
|
3
|
37
|
30.625
|
1.2082
|
| 5
|
4
|
4
|
26
|
32.000
|
0.8125
|
| 6
|
2011/1
|
5
|
30
|
33.375
|
0.8989
|
| 7
|
2
|
6
|
38
|
34.500
|
1.1014
|
| 8
|
3
|
7
|
42
|
34.875
|
1.2043
|
| 9
|
4
|
8
|
30
|
34.875
|
0.8602
|
| 10
|
2012/1
|
9
|
29
|
36.000
|
0.8056
|
| 11
|
2
|
10
|
39
|
37.625
|
1.0365
|
| 12
|
3
|
11
|
50
|
38.375
|
1.3029
|
| 13
|
4
|
12
|
35
|
38.500
|
0.9091
|
| 14
|
2013/1
|
13
|
30
|
38.625
|
0.7767
|
| 15
|
2
|
14
|
39
|
39.000
|
1.0000
|
| 16
|
3
|
15
|
51
|
39.125
|
1.3035
|
| 17
|
4
|
16
|
37
|
39.375
|
0.9397
|
| 18
|
2014/1
|
17
|
29
|
40.250
|
0.7205
|
| 19
|
2
|
18
|
42
|
40.875
|
1.0275
|
| 20
|
3
|
19
|
55
|
41.250
|
1.3333
|
| 2l
|
4
|
20
|
38
|
41.625
|
0.9129
|
| 22
|
2015/1
|
21
|
31
|
41.625
|
0.7447
|
| 23
|
2
|
22
|
43
|
4i.875
|
1.0269
|
| 24
|
3
|
23
|
54
|
—
|
—
|
| 25
|
4
|
24
|
41
|
—
|
—
|
其中,
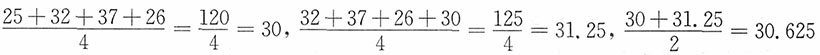
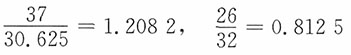
为计算各比值的平均值和季节指数,需要将表1中的比值再按季度重新排列,结果如表2所示。
| 表2 计算过程
|
|
|
A
|
B
|
C
|
D
|
E
|
| 1
|
年份
|
季度
|
| 2
|
1
|
2
|
3
|
4
|
| 3
|
2010
|
—
|
—
|
1.2082
|
0.8125
|
| 4
|
2011
|
0.8989
|
1.10144
|
1.2043
|
0.8602
|
| 5
|
2012
|
0.8056
|
1.0365
|
1.3029
|
0.9091
|
| 6
|
2013
|
0.7767
|
1.0000
|
1.3035
|
0.9397
|
| 7
|
2014
|
0.7205
|
1.0275
|
1.3333
|
0.9129
|
| 8
|
2015
|
0.7447
|
1.0269
|
—
|
—
|
| 9
|
合计
|
3.9464
|
5.1924
|
6.3522
|
4.4344
|
| 10
|
平均
|
0.7893
|
1.0385
|
1.2704
|
0.8869
|
| 11
|
季节指数
|
0.7922
|
1.0424
|
1.2752
|
0.8902
|
其中,
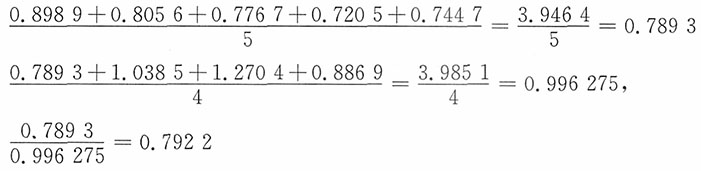
为反映啤酒销售量的季节变动,可以将季节指数绘制成图形,如图2所示,啤酒销售量的旺季是3季度,淡季是1季度。
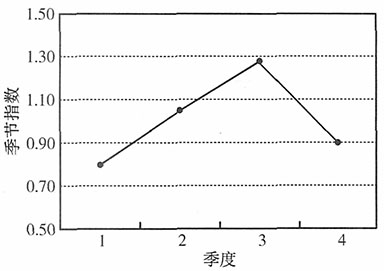 图2 啤酒销售量季节变动图
图2 啤酒销售量季节变动图
2. 用按季平均法计算季节指数。
解:用按季平均法求季节指数的过程如表1所示。
表1 计算过程 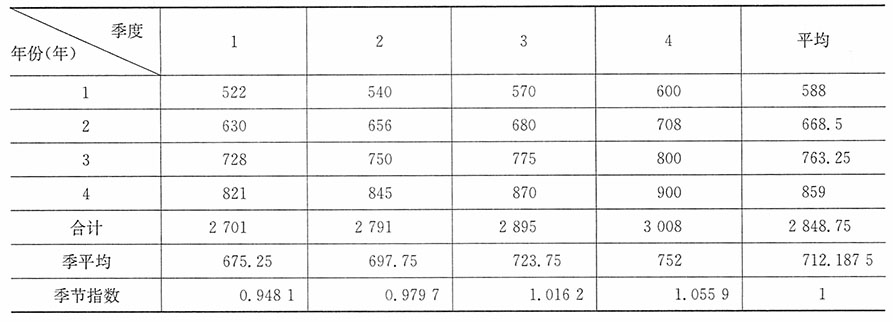
3. 用长期趋势剔除法计算季节指数。
某企业产量季度销量 
解:用长期趋势剔除法求季节指数的过程如表2、表3所示。
| 表2 季节指数的计算过程
|
| 时间序号t
|
Y
|
预测值
|
Y/T=S×I
|
| 1
|
522
|
524.8088
|
0.9946
|
| 2
|
540
|
549.7926
|
0.9822
|
| 3
|
570
|
574.7765
|
0.9917
|
| 4
|
600
|
599.7603
|
1.0004
|
| 5
|
630
|
624.7441
|
1.0084
|
| 6
|
656
|
649.7279
|
1.0097
|
| 7
|
680
|
674.7118
|
1.0078
|
| 8
|
708
|
699.6956
|
1.0119
|
| 9
|
728
|
724.6794
|
1.0046
|
续表
|
| 时间序号t
|
Y
|
预测值
|
Y/T=S×I
|
| 10
|
750
|
749.6632
|
1.0004
|
| 11
|
775
|
774.6471
|
1.0005
|
| 12
|
800
|
799.6309
|
1.0005
|
| 13
|
821
|
824.6147
|
0.9956
|
| 14
|
845
|
849.5985
|
0.9946
|
| 15
|
870
|
874.5824
|
0.9948
|
| 16
|
900
|
899.5662
|
1.0005
|
表3 季平均季节指数计算
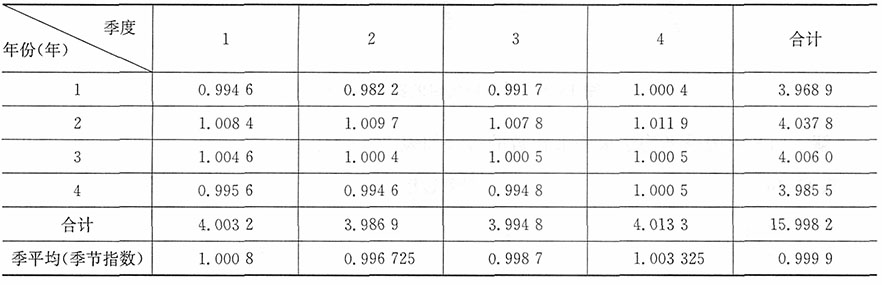
| 两种商品基期和报告期数据 |
| 商品名称 | 计量单位 | 销售量q | 价格p |
| 基期q0 | 报告期q1 | 基期p0 | 报告期p1 |
| 甲 | 千克 | 400 | 350 | 80 | 85 |
| 乙 | 千克 | 600 | 560 | 36 | 43 |
要求:4. 计算两种商品的拉氏价格总指数。
解:两种商品的拉氏价格总指数为
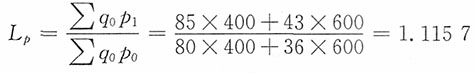
5. 计算两种商品的帕氏价格总指数。
解:两种商品的帕氏价格总指数为
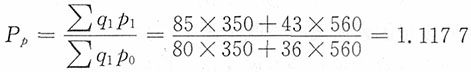
6. 比较拉氏价格总指数与帕氏价格总指数计算结果的差异,并指出产生差异的原因。
解:由于销售量固定在不同的时期,拉氏价格总指数和帕氏价格总指数的计算结果存在一定差异。拉氏价格总指数把作为权数的销售量固定在基期;帕氏价格总指数把作为权数的销售量固定在报告期。拉氏指数计算结果偏小,帕氏指数计算结果偏大。
7. 计算两种商品的价格理想指数。
解:两种商品的价格理想指数为
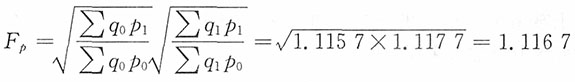
8. 市场上的5种商品销售价格与销售量资料如表所示,试计算拉氏指数和帕氏指数。
| 销售价格与销售量资料 |
| 商品 | 计量 | 商品价格 | 销售量 |
| 单位 | 基期 | 报告期 | 基期 | 报告期 |
| 大米 | 百公斤 | 300 | 360 | 2400 | 2600 |
| 猪肉 | 公斤 | 18 | 20 | 84000 | 95000 |
| 食盐 | 500克 | 1 | 0.8 | 10000 | 15000 |
| 服装 | 件 | 100 | 130 | 24000 | 23000 |
| 电视 | 台 | 4500 | 4300 | 510 | 612 |
解:拉氏销售价格指数和拉氏销售量指数分别为

帕氏销售价格指数和帕氏销售量指数分别为
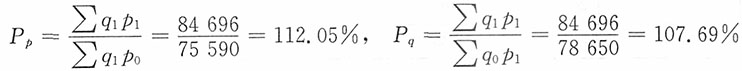
9. 试计算某市居民消费价格总指数,计算结果如表所示。
| 某市居民消费价格总指数计算 |
| 商品类别 | 类指数i | 固定权数W | iW |
| 一、食品类 | 104.15% | 42% | 43.743% |
| 二、衣着类 | 95.46% | 15% | 14.319% |
| 三、家庭设备用品及服务类 | 102.70% | 11% | 11.297% |
| 四、医疗保健和个人用品类 | 110.43% | 3% | 3.313% |
| 五、交通和通信工具类 | 98.53% | 4% | 3.941% |
| 六、娱乐教育用品及服务类 | 101.26% | 5% | 5.063% |
| 七、烟酒及用品类 | 103.50% | 14% | 14.490% |
| 八、居住类 | 108.74% | 6% | 6.524% |
| 合计 | — | 100% | 102.69% |
解:居民消费价格总指数采用固定加权平均指数公式,即
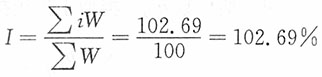
。计算结果表明,该市居民消费价格总指数报告期比基期平均上涨了2.69%。
10. 下表是某商场甲、乙、丙三种商品2007年和2008年的资料,其中,下标0表示2007年,下标1表示2008年,p表示价格,q表示销售量。采用指数体系对该数据进行因素分析。
| 甲、乙、丙2007年、2008年的资料 |
| 商品名称 | 计量单位 | 销售量 | 价格(元) | 销售额(万元) |
| q0 | q1 | p0 | p1 | p0q0 | p1q1 | 假定 |
| p0q1 | p1q0 |
| 甲 | 件 | 200 | 300 | 60 | 60 | 1.2 | 1.8 | 1.8 | 1.2 |
| 乙 | 双 | 400 | 500 | 20 | 30 | 0.8 | 1.5 | 1.0 | 1.2 |
| 丙 | 米 | 500 | 600 | 70 | 80 | 3.5 | 4.8 | 4.2 | 4.0 |
| 合计 | — | — | — | — | — | 5.5 | 8.1 | 7.0 | 6.4 |
解:三种商品销售额的变动:
销售额指数
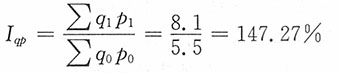
2008年与2007年相比,三种商品销售额增长了47.27%,增加的绝对值为
∑q
1p
1-∑q
0p
0=8.1-5.5=2.6(万元)
其中,(1)销售量变动的影响:销售量指数
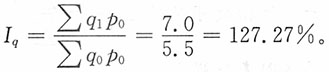
计算结果表明,2008年与2007年相比,该商场三种商品销售量平均增长了27.27%,销售量的上升使销售额增加的绝对值为
∑q
1p
0-∑q
0p
0=7.0-5.5=1.5(万元)
(2)销售价格变动的影响:销售价格指数
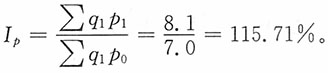
计算结果表明,2008年与2007年相比,三种商品销售价格平均上升了15.71%,销售价格的上升使销售额增加的绝对值为
由此可见,销售额增长了47.27%,是销售量平均增长27.27%和销售价格平均增长15.71%共同影响的结果,即147.27%=127.27%×115.71%。
而销售额增加了2.6万元,是销售量增长使其增加1.5万元和销售价格上升使其增加1.1万元共同影响的结果,即2.6万元=1.5万元+1.1万元。
11. 某企业多元化经营中生产三种产品,其基期与报告期产量和出厂价格如表所示。
| 三种产品相关资料 |
产品
名称 | 计量
单位 | 产量 | 出厂价格(元) | 产值(元) |
| q0 | q1 | p0 | p1 | p0q0 | p1q1 |
| 甲 | 吨 | 300 | 3600 | 2000 | 2200 | 600000 | 792000 |
| 乙 | 千米 | 400 | 420 | 3600 | 4000 | 144000 | 168000 |
| 丙 | 千块 | 4 | 5 | 4000 | 4000 | 16000 | 20000 |
| 合计 | — | — | — | — | — | 7456000 | 962000 |
试以产量和出厂价格为因素,完成总产值指数的分解。
解:
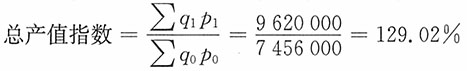
总产值增长绝对数=∑q
1p
1-∑q
0p
0=9620000-7456000=2164000(元)
这表示与基期相比,报告期总产值增长了29.02%,绝对值增长了216.4万元。产量和出厂价格的变动为

可见,在这个过程中,产品产量增长了17.11%,由于产量增长而导致的产值增长绝对数为127.6万元;出厂价格增长了10.17%,由于出厂价格增长而导致的产值增长绝对数为88.8万元。即存在
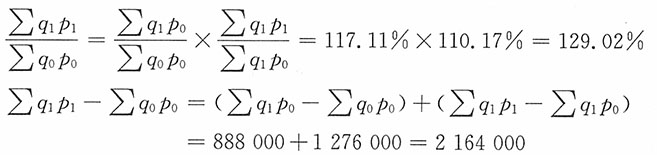
这说明总产值指数变动是由产量指数和出厂价格指数共同变动作用而成的,其中产量指数变动对总产值指数变动造成的影响为117.11%,出厂价格指数变动对总产值指数变动造成的影响为110.17%,二者共同作用使得总产值指数变动为129.02%。同理,可以解释产量和出厂价格两因素对总产值绝对数的变动情况。
12. 某企业生产情况如表所示。要求:遵循综合指数编制的一般原则,计算:(1)三种产品的产量总指数和价格总指数。(2)进行总产值变动的因素分析。
| 某企业生产情况 |
| 产品名称 | 计量单位 | 销售量 | 价格(元) |
| 基期 | 报告期 | 基期 | 报告期 |
| 甲 | 台 | 360 | 300 | 1500 | 1100 |
| 乙 | 件 | 200 | 200 | 1000 | 800 |
| 丙 | 只 | 160 | 140 | 250 | 250 |
解:根据已知资料可得综合指数计算表,如表所示。
| 综合计算表
|
| 产品名称
|
q0p0
|
q1p0
|
q1p1
|
| 甲
|
330000
|
396000
|
540000
|
| 乙
|
160000
|
160000
|
200000
|
| 丙
|
30 800
|
40000
|
40000
|
| 合计
|
520800
|
596000
|
780000
|
(1)产量总指数
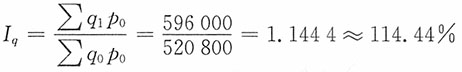
价格总指数
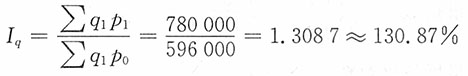
(2)产值变动因素分析:
产值总指数
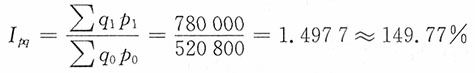
相对数分析

,149.77%≈114.44%×130.87%
即该企业总产值上涨49.77%,是由于产量增长14.44%和价格上涨30.87%两个因素作用的结果。
绝对数分析
∑q
1p
1-∑q
0p
0=(∑q
1p
0-∑q
0p
0)+(∑q
1p
1-∑q
1p
0),
259200=75200+184000
即该企业总产值增加259200元,是由于产量增长使产值增加75200元和价格上涨使产值增加184000元的结果。
13. 某商店三种产品的销售情况资料,如表所示。
| 产品销售情况 |
| 商品名称 | 计量单位 | 价格(元) | 生产量 |
| 基期 | 报告期 | 基期 | 报告期 |
| 皮鞋 | 双 | 25 | 28 | 4000 | 5000 |
| 呢大衣 | 件 | 140 | 160 | 500 | 550 |
| 线手套 | 只 | 0.5 | 0.6 | 800 | 1000 |
要求:
(1)计算商品价格和销售量个体指数。(2)分析销售量总变动程度和价格总变动程度(从相对数和绝对数两方面)。
解:计算过程如表所示。
| 计算过程
|
| 商品名称
|
价格
|
销售量
|
基期
|
销售额
|
假定期
|
| p0
|
p1
|
q0
|
q1
|
p0q0
|
p1q1
|
p0q1
|
| 皮鞋
|
25
|
28
|
4000
|
5000
|
100000
|
140000
|
125000
|
| 呢大衣
|
140
|
160
|
500
|
550
|
70000
|
88000
|
77000
|
| 线手套
|
0.5
|
0.6
|
800
|
1000
|
400
|
600
|
500
|
| 合计
|
|
|
|
|
170400
|
228600
|
202500
|
(1)这三种商品的价格和销售量个体指数:
皮鞋
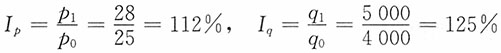
呢大衣
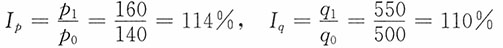
线手套
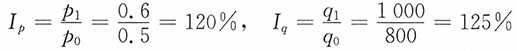
(2)销售量总变动为
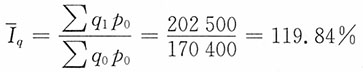
∑q1p0-∑q0p0=32100(元)
即销售量增长18.84%,使销售量增加32100元。
价格总变动为
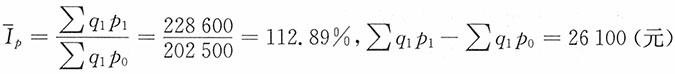
即销售价格增长12.89%,使销售额增加26100元。
14. 某企业利润额资料如表所示。试分析销售量q、销售价格p、利润率r对利润总额T的影响。
| 利润资料 |
| 产品类别 | 计量单位 | 销售量 | 销售价格(元) | 利润率(%) |
| 基期 | 报告期 | 基期 | 报告期 | 基期 | 报告期 |
| 1 | 万件 | 450 | 500 | 700 | 770 | 8 | 9 |
| 2 | 万件 | 500 | 520 | 350 | 350 | 7 | 11 |
| 3 | 台 | 900 | 1080 | 100 | 110 | 12 | 10 |
解:(1)净利润总额:基期T
0=∑q
0p
0r
0=48250(元)
报告期T1=∑q
1p
1r
1=66550(元)
利润额总指数
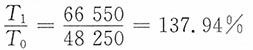
利润额增长绝对数T
1-T
0=66550-48250=18300(元)
即利润额报告期比基期增长了37.94%,绝对额增加为18300元。
(2)销售量指数:
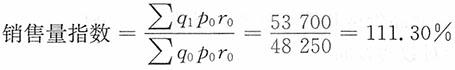
即销售量报告期比基期提升了11.30%,由此带来的利润额增长为
∑q
1p
0r
0-∑q
0p
0r
0=53700-48250=5450(元)
(3)销售价格指数:
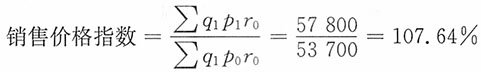
即销售价格报告期比基期上涨了7.64%,由此导致的利润额增长为
∑q
1p
1r
0-∑q
1p
0r
0=57800-53700=4100(元)
(4)利润率指数:

即利润率报告期比基期提高了15.14%,由此形成的利润额增长为
∑q
1p
1r
1-∑q
1p
1r
0=66550-57800=8750(元)
(5)利润额总指数构成分析:基于上述的计算结果进行综合分析得
137.94%=111.30%×107.67%×115.14%,18300=5450+4100+8750
由此说明,在报告期,由于销售量增加了11.30%,销售价格上涨了7.64%,利润率提高了15.14%等三个方面的综合作用结果,使得企业总利润额提高了37.94%;从绝对数上看,利润额增加18300元来自销售量提升带来的5450元,销售价格上涨导致的4100元和利润率提高形成的8750元。
进一步分析可见,在企业利润额增加的过程中,利润率因素带来的利润额增加约占50%,销售量因素带来的利润额增加约占30%,销售价格因素带来的利润额增加约占20%。这说明企业的发展处于一个比较好的态势,企业具有较强的市场竞争能力,其利润创造是通过内涵建设而产生的,不是一味依赖于生产要素的投入和市场价格波动的投机而产生的。
15. 某机械厂所属两个分厂的某机器产品成本资料如表所示。试分析该厂某产品总平均单位成本的变动受各分厂成本水平变动以及产量结构变动的影响情况。
| 产品成本资料 |
| 分厂 | 单位成本(元) | 产量(台) | 总成本(元) |
| x0 | x1 | f0 | f1 | x0f0 | x1f1 | x0f1 |
| 一分厂 | 1200.0 | 1220.0 | 70 | 70 | 84000 | 85400 | 84000 |
| 二分厂 | 1000.0 | 900.0 | 30 | 130 | 30000 | 117000 | 130000 |
| 全厂 | — | — | 100 | 200 | 114000 | 202400 | 214000 |
解:基期平均单位成本
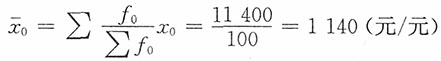
报告期平均单位成本
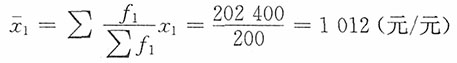
假定平均单位成本
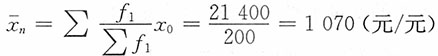
该机械厂平均单位成本变动分析:
总平均水平指数
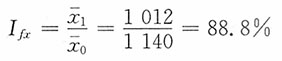
总平均水平变动额
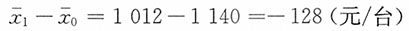
其中,(1)各分厂产量结构变动对全厂平均单位成本变动的影响:
结构变动指数
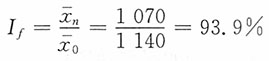
各分厂产量结构变动使全厂单位成本变化为:
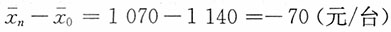
。
(2)各分厂单位成本变动对全厂平均单位成本变动的影响:
组水平变动指数
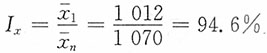
各分厂单位成本变动使全厂单位成本变化为:
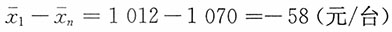
。
计算结果表明,全厂平均单位成本下降11.2%,产量结构变动使全厂单位成本下降6.1%,各分厂单位成本下降使全厂单位成本下降5.4%,两者共同影响的结果,即88.8%=93.9%×94.6%
从绝对数上看,全厂平均单位成本降低了128元,产量结构变动使全厂单位成本降低70元,各分厂单位成本下降使全厂单位成本降低58元,即-128元/台=-58元/台+(-70)元/台。
16. 某理财组合由两种股票组成,其股票价格、持股数量资料如表所示。试分析该理财组合收益变动受股票价格变动以及持股数量变动的影响情况。
| 股票价格及持股情况 |
| | 股票价格(元/股) | 持股数量(股) |
| 基期 | 报告期 | 基期 | 报告期 |
股票一
股票二 | 22
35 | 28
32 | 1000
800 | 1200
700 |
解:可变结构指数

固定构成指数

结构影响指数
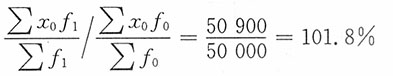
所以,存在
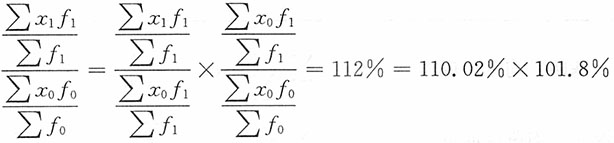
即理财组成收益增长12%,其中由于股价变动造成的收益增长为10.02%,由持股数量变动造成的收益增长为1.8%。
该理财组合收益变动绝对值为
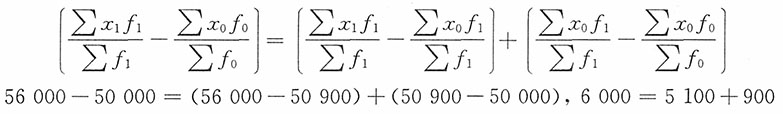
即理财组合收益增加6000元,其中,由于股价变动造成的收益增长为5100元,由于持股数量变动造成的收益增长为900元。
17. 某公司下属三个工厂生产同种产品,已知基期产品总成本为1084.08万元,报告期产品总成本为1153.45万元,报告期与基期相比,单位产品成本降低3.254%,总产量增长9.645%,又知该公司报告期总产量为10800吨。试从相对数和绝对数两方面分析该公司产品总成本变动中单位成本、产品结构和产品总量三个因素变动的影响。
解:已知:∑q
0p
0=1084.08,∑q
1p
1=1153.45,∑q
1=10800
而
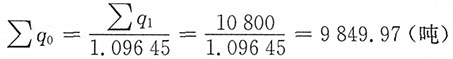
单位产品成本总指数
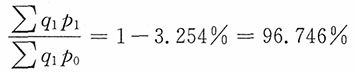
而
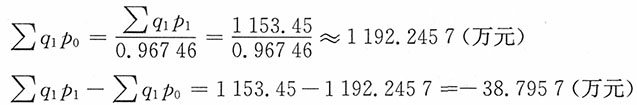
产品总成本指数

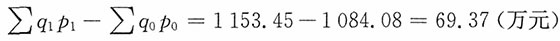
产量总指数
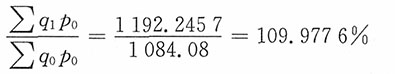
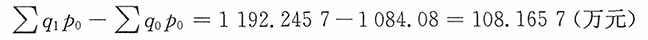
综上:106.399%=109.9776%×96.746%,69.37万元=108.1657万元-38.7957万元
再者,基期的平均单位成本
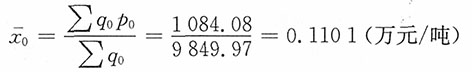
报告期的平均单位成本
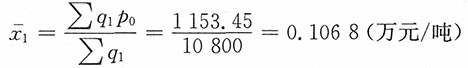
而
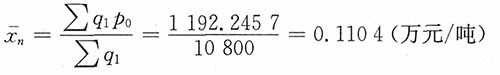
可变构成指数
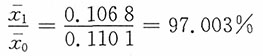
绝对量增减
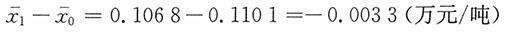
结构变动指数
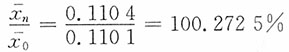
绝对量增减
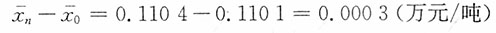
固定构成指数
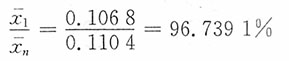
绝对量增减
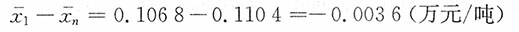
综上:97.003%=100.2725%×96.7391%,-0.0033万元/吨=0.0003万元/吨-0.0036万元/吨。
18. 现以部分资料(见下表)说明消费品部分价格总指数的编制和计算过程。
| 消费品部分价格总指数的编制 |
| 商品类别及名称 | 代表规格品 | 计量单位 | 平均价格(元) | 权数W
(%) | 指数i
(%) | iW |
| p0 | p1 |
| 总指数 | | | | | 100 | 111.6 | 11159.8% |
| 一、食品类 | | | | | 38 | 116.2 | 4415.6% |
| 1.粮食 | | | | | 35 | 105.3 | 3685.5% |
| 细粮 | | | | | 65 | 105.6 | 6864.0% |
| 面粉 | 标准 | kg | 2.40 | 2.52 | 40 | 105.0 | 4200.0% |
| 大米 | 梗米标一 | kg | 3.50 | 3.71 | 60 | 106.0 | 6360.0% |
| 粗粮 | | | | | 35 | 104.8 | 3668.0% |
| 2.副食品 | | | | | 45 | 125.4 | 5643.0% |
| 3.其他食品 | | | | | 20 | 114.8 | 2296.0% |
| 二、饮料、烟酒 | | | | | 5 | 126.0 | 630.0% |
| 三、服装、鞋帽 | | | | | 10 | 115.2 | 1152.0% |
| 四、纺织品 | | | | | 3 | 99.3 | 297.9% |
| 五、家用电器及音像器材 | | | | | 8 | 94.2 | 753.6% |
| 六、文化办公用品 | | | | | 2 | 110.4 | 220.8% |
| 七、日用品 | | | | | 11 | 109.5 | 1204.5% |
| 八、体育娱乐用品 | | | | | 2 | 98.1 | 196.2% |
| 九、交通、通信用品 | | | | | 1 | 91.1 | 91.1% |
| 十、家具 | | | | | 2 | 97.8 | 195.6% |
| 十一、化妆品 | | | | | 1 | 98.9 | 98.9% |
| 十二、金银珠宝 | | | | | 3 | 108.6 | 325.8% |
| 十三、中西药品及医疗保健用品 | | | | | 7 | 116.4 | 814.8% |
| 十四、书报杂志及电子出版物 | | | | | 2 | 108.6 | 217.2% |
| 十五、燃料 | | | | | 3 | 105.6 | 316.8% |
| 十六、建筑材料及五金电料 | | | | | 2 | 114.5 | 229.0% |
解:(1)计算出各代表规格品的价格指数。例如,面粉价格指数为
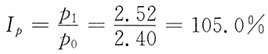
(2)根据各代表规格品的价格指数及给出的相应权数,加权算术平均计算小类指数。例如,细粮类价格指数为
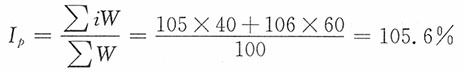
(3)根据各小类指数及相应的权数,加权算术平均计算中类指数。例如,粮食价格指数为
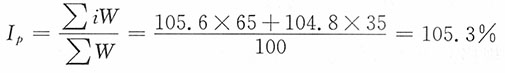
(4)根据各中类指数及相应的权数,加权算术平均计算大类指数。例如,食品类价格指数为
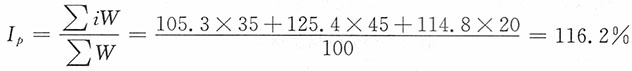
(5)根据各大类指数及相应的权数,加权算术平均计算总指数。即
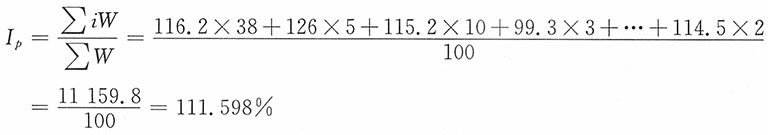
19. 某商店销售的三种商品2011年价格分别是2010年的106%、94%、110%,三种商品销售额2011年分别为80000元、25000元、14000元。三种商品物价指数是多少?
解:物价指数
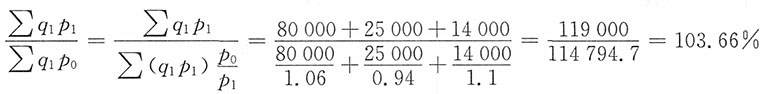
20. 某公司下属三个工厂生产某种产品的情况如表所示。
| 甲、乙、丙三厂生产某种产品的情况 |
| 企业名称 | 单位产品成本(万元/吨) | 产量(吨) |
| 上年 | 来年 | 上年 | 本年 |
| 甲厂 | 98 | 95 | 450 | 560 |
| 乙厂 | 101 | 104 | 300 | 250 |
| 丙厂 | 108 | 105 | 200 | 190 |
根据上表资料,从相对数和绝对数两个方面计算和分析该公司产品成本总额变动中单位成本、总体结构和产品总量三个因素变动的影响。
解:易见∑q
0p
0=98×450+101×300+108×200=96000
∑q
1p
1=95×560+104×250+105×190=99150
∑q
1p
0=98×560+101×250+108×190=100650
总成本指数
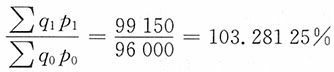
总成本增加∑q
1p
1-∑q
0p
0=99150-96000=3150(万元)
产量总指数
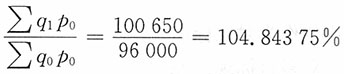
影响总成本增加∑q
1p
0-∑q
0p
0=100650-96000=4650(万元)
单位产品成本总指数
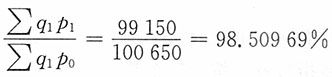
影响总成本减少∑q
1p
1-∑q
1p
0=99150-100650=1500(万元)
综上:103.28125%=104.84375%×98.50969%,3150=4650-1500
再者,基期的平均单位成本
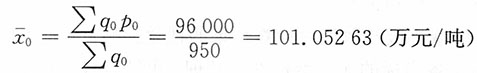
报告期的平均单位成本
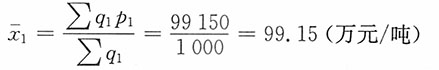
而
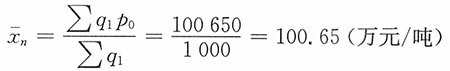
可变构成指数
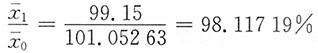
绝对量增减
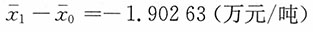
结构变动指数
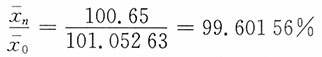
绝对量增减
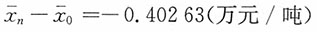
固定构成指数
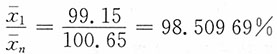
绝对量增减
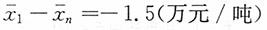
综上:98.11719%=99.60156%×98.50969%
-1.90263元/吨=-0.40263万元/吨-1.5万元/吨

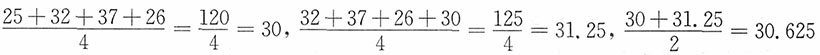
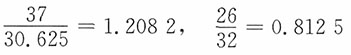 为计算各比值的平均值和季节指数,需要将表1中的比值再按季度重新排列,结果如表2所示。
为计算各比值的平均值和季节指数,需要将表1中的比值再按季度重新排列,结果如表2所示。
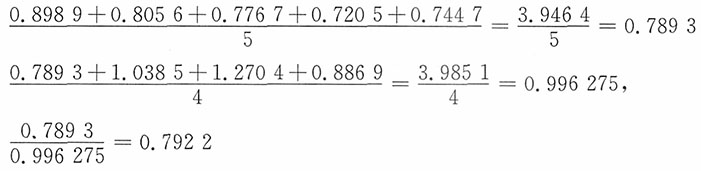




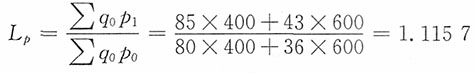
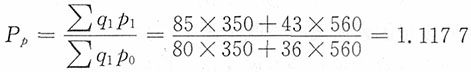
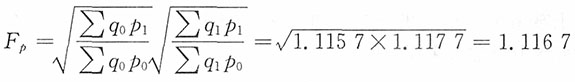

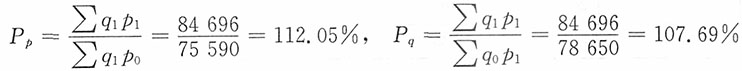
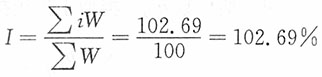 。计算结果表明,该市居民消费价格总指数报告期比基期平均上涨了2.69%。
。计算结果表明,该市居民消费价格总指数报告期比基期平均上涨了2.69%。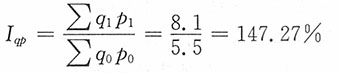
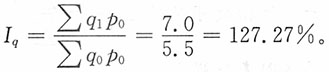
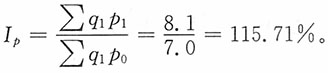
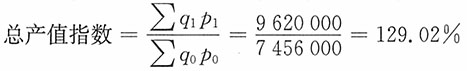

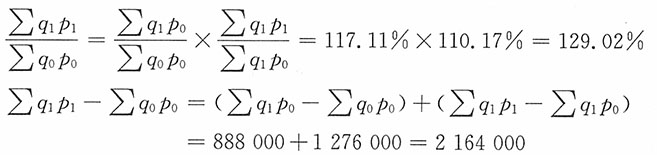
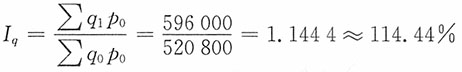
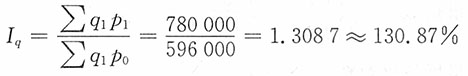
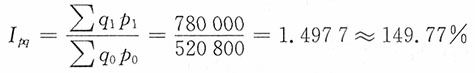
 ,149.77%≈114.44%×130.87%
,149.77%≈114.44%×130.87%
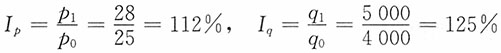
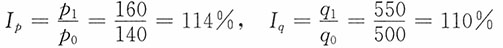
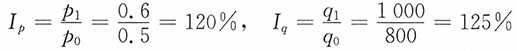
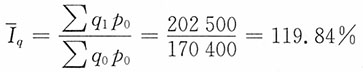
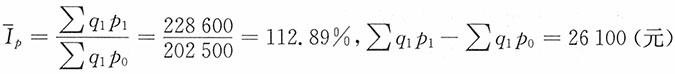
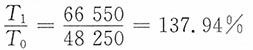
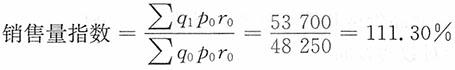
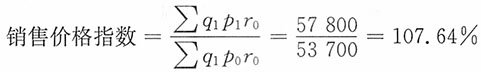

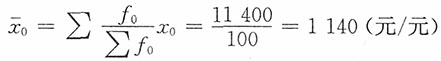
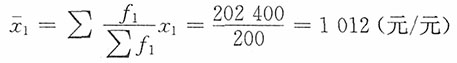
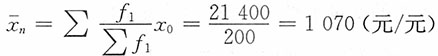
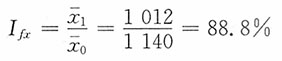
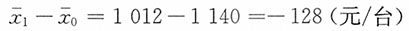
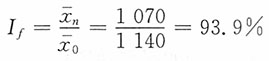
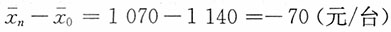 。
。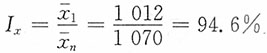
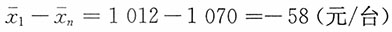 。
。