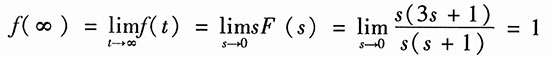计算题求下列周期信号的基波角频率Ω和周期T。1. cos2t+sin4t;
解:因为2和4的最大公约数是2,所以cos2t+sin4t的基波角频为Ω=2,
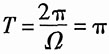
。
2. cos2πt+cosπt+cos5πt;
解:因为2π、3π、5π的最大公约数是π,所以信号cos2πt+cos3πt+cos(5πt)的基波角频率为Ω=π,
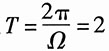
。
3.
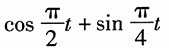
解:因为
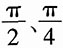
的最大公约数是
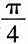
,所以信号
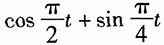
的基波角频率为
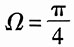
,
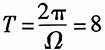
。
4.
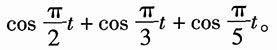
5. 求下图所示离散系统(未标的支路增益均为1)的系统函数H(z)。
解:(1)图(a)中共有两个回路,回路增益分别为
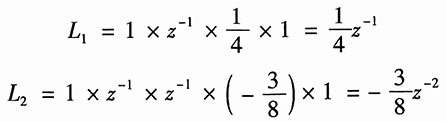
并且它们没有两个以上互不接触的回路,所以信号流图的特征多项式为
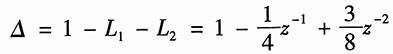
它有两条前向通路,其增益分别为
P
1=1×1×2×1=2
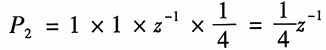
并知各回路均与该两个前向通路相接触,则其特征余子式为
Δ
1=1,Δ
2=1
利用梅森公式,可得该系统的系统函数为
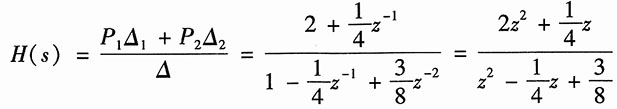
(2)图(b)中共有两个回路,回路增益分别为
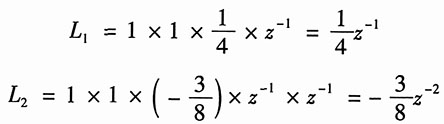
并且它们没有两个以上互不接触的回路,所以信号流图的特征多项式为
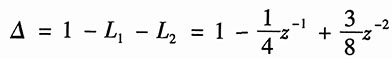
它有两条前向通路,其增益分别为
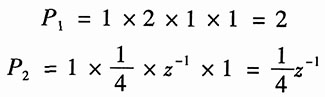
并知各回路均与该两个前向通路相接触,则其特征余子式为
Δ
1=1,Δ
2=1
利用梅森公式,可得该系统的系统函数为
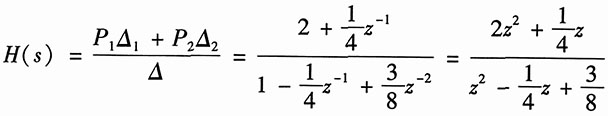
6. 写出下图所示各序列的闭合形式表示式。
解:由上图可知:
(a)f(k)=ε(k+2)
(b)f(k)=ε(k-3)-ε(k-7)
(c)f(k)=ε(2-k)
(d)f(k)=(-1)kε(k)
7. 用直接计算傅里叶系数的方法,求下图所示周期函数的傅里叶系数(三角形式或指数形式)。
解:(1)由图知T=4,所以
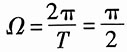
。
直接使用公式:
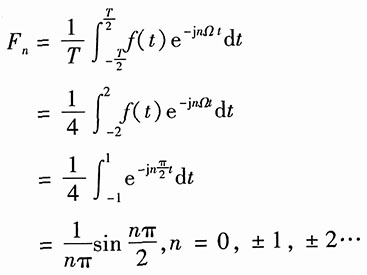
(2)由题图看出
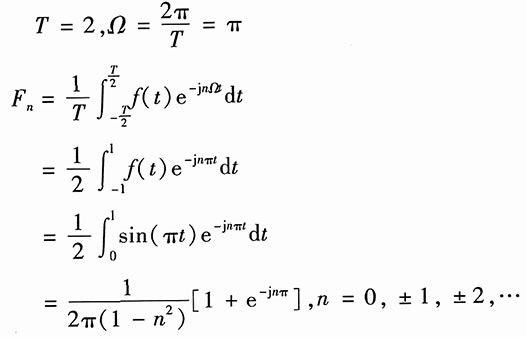
8. 为用计算机求解微分方程,需要将连续信号离散化。若描述系统的一阶微分方程为
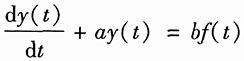
(1)
在t=kT各时刻激励和响应的取样值分别为f(kT)、y(kT),并假设时间间隔T(称为取样周期)足够小,那么在t=kT时刻y(t)的导数可近似为
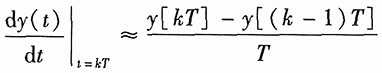
这样,上述微分方程可写为
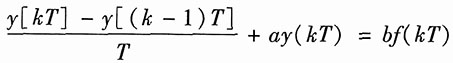
稍加整理,得

或写为
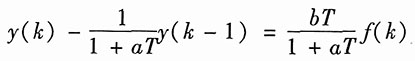
(2)
若a=b=1,f(t)=ε(t),求微分方程式(1)的零状态响应;若取a=b=1,T=0.25s,f(k)=ε(k),求差分方程式(2)的零状态响应,并将二者进行比较。
解:y'(t)+ay(t)=f(t) (3)
因为
a=1,f(t)=ε(t)
所以
y'(t)+y(t)=ε(t) (4)
式(4)的齐次解为
y
h(t)=ce
-tε(t)
式(4)的特解为
y
p(t)=1
所以
y(t)=y
h(t)+y
p(t)
=[ce
-t+1]ε(t)
因为是零状态而且式(4)右端不包含冲激项,所以
y(0
+)=0
代入上式,得
c+1=0,c=-1
y(t)=(1-e
-t)ε(t)即式(1)的零状态响应。
求差分方程式(2):
因为
a=b=1,T=0.25,f(k)=ε(k)
所以方程式(2)写为
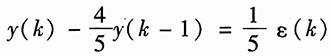
(5)
方程式(5)的零状态响应写为
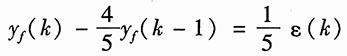
(6)
式(6)的齐次解为
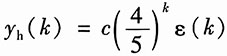
式(5)的特解为
y
p(k)=1
所以
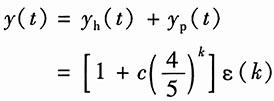
由式(5)求初始值:
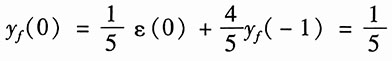
将y(0)代入上式,解得
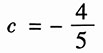
所以
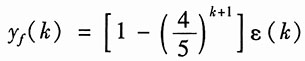
9. y"(t)+3y'(t)+2y(t)=f'(t);
解:对方程两边同时进行傅里叶变换,得
(jω)
2Y(jω)+3(jω)Y(jω)+2Y(jω)=(jω)F(jω)
所以

10. y"(t)+5y'(t)+6y(t)=f'(t)+4f(t)。
解:方程两边同时进行傅里叶变换,得
(jω)
2Y(jω)+5(jω)Y(jω)+6Y(jω)=(jω)F(jω)+4F(jω)
所以
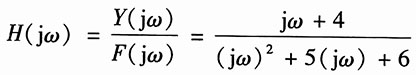
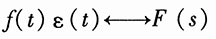 ,且有实常数a>0,b>0,试证明:
,且有实常数a>0,b>0,试证明:
11.
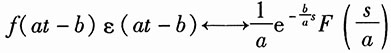
证明:利用性质证明。
由于
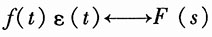
,则当b>0,利用时移特性,得
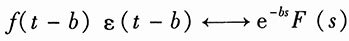
再利用尺度变换,得

12.
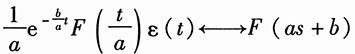
证明:由于

,则利用尺度变换,当a>0时,有
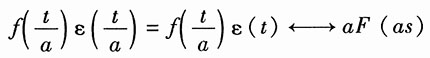
然后再利用复频域特性,得
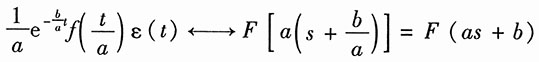
也可直接利用定义证明。
13. 已知图1所示系统的输入为
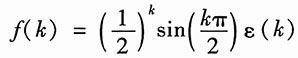
求系统的零状态响应y
zs(k)。
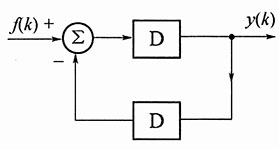
图1
解:画出系统的Z域框图(图2)。
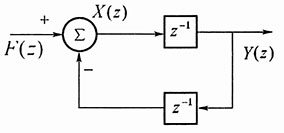
图2
设加法器的输出为X(z),则在加法器的输出端可列出方程:
X(z)=F(z)-z
-1Y(z)
于是,系统输出的象函数为
Y(z)=z-1X(z)=z
-1[F(z)-z
-1Y(z)]
解得
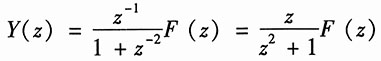
由于

因此系统零状态响应的象函数为

取逆变换,得系统的零状态响应为
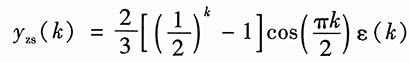
14. 描述某LTI离散系统的差分方程为
y(k)-y(k-1)-2y(k-2)=f(k)
已知y(-1)=-1,
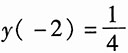
,f(k)=ε(k),求该系统的零输入响应y
zi(k),零状态响应y
zs(k)及全响应y(k)。
解:设y(k)的Z变换为Y(z),f(k)的Z变换为F(z)。对差分方程取单边Z变换,利用移序特性,得
Y(z)-[z
-1Y(z)+y(-1)]-2[z
-2Y(z)+z
-1y(-1)+y(-2)]=F(z)
解得
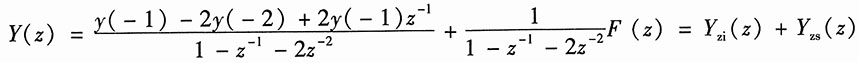
其中
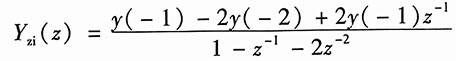
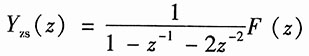
将初始状态y(-1)=-1,
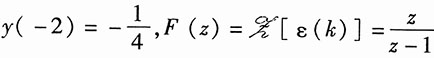
代入并整理,得
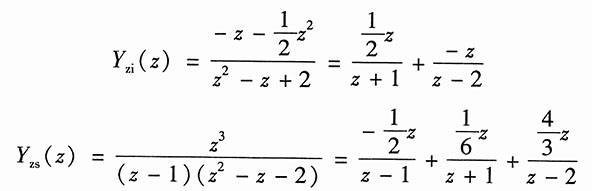
对以上两式取逆变换,得系统的零输入响应和零状态响应分别为
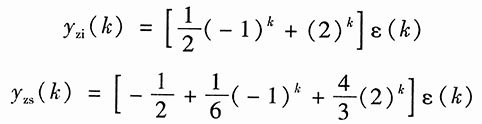
系统的全响应为
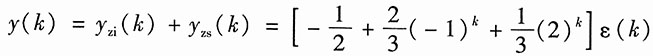
15.
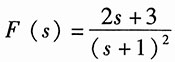
解:因象函数F(s)为真分式,则其原函数f(t)中不含δ(t)及其各阶导数,由初值定理,可得
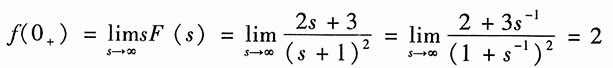
由于F(s)的极点s=-1位于左半平面,故终值存在。由终值定理,得
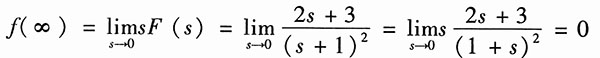
16.
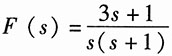
解:因F(s)为s的实系数有理真分式,则其函数f(t)中不包含δ(t)及其各阶导数,则由初值定理可得
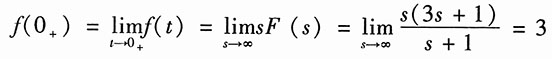
由于极点s=-1在左半平面,原点上的极点s=0为一阶,故终值存在,即