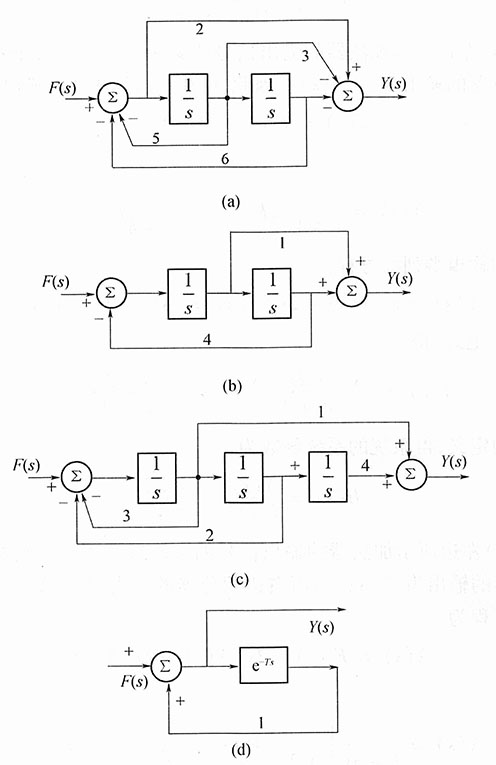
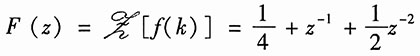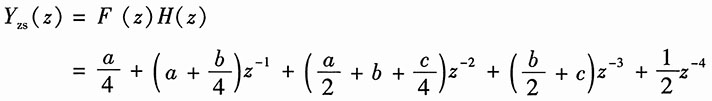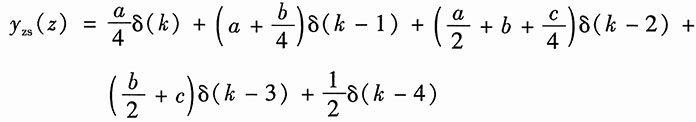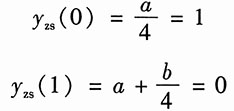计算题1. 写出下图所示各s域框图所描述系统的系统函数H(s)(图(d)中e
-Ts为延时单元的s域模式)。
解:(1)设图(a)左边所示加法器的输出信号的象函数为X(s),则左边积分器的输出为s
-1X(s),而右边积分器的输出为s
-2X(s)。因此,可在左边加法器的输出端列出方程为
X(s)=F(s)-5s
-1X(s)-6s
-2X(s)
解得
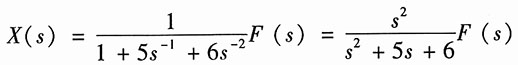
(1)
在右边加法器的输出端列写方程
Y(s)=2X(s)-3s
-1X(s)-4s-4s
-2X(s)=(2-3s
-1-4s
-2)X(s)
将式(1)代入上式,得
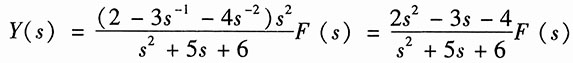
根据系统函数的定义,得系统的系统函数为
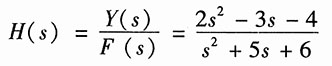
(2)设图(b)左边所示加法器的输出信号的象函数为X(s),则左边积分器的输出为s
-1X(s),而右边积分器的输出为s
-2X(s)。因此,可在左边加法器的输出端列出方程为
X(s)=F(s)-4s
-2X(s)
解得
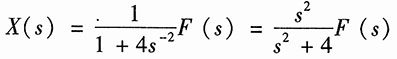
(2)
在右边加法器的输出端列写方程:
Y(s)=s
-1X(s)+2s
-2X(s)=(s
-1+2s
-2)X(s)
将式(2)代入上式,得
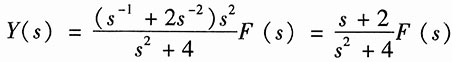
根据系统函数的定义,得系统的系统函数为
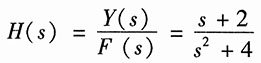
(3)设图(c)左边所示加法器的输出信号的象函数为X(s),则左边积分器的输出为s
-1X(s),中间积分器的输出为s
-2X(s),而右边积分器的输出为s
-3X(s)。因此,可在左边加法器的输出端列出方程为
X(s)=F(s)-3s
-1X(s)-2s
-2X(s)
解得
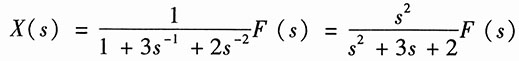
(3)
在右边加法器的输出端列写方程:
Y(s)=s
-1X(s)+4s
-3X(s)=(s
-1+4s
-3)X(s)
将式(3)代入上式,得
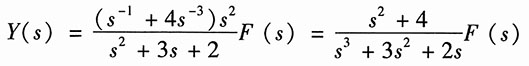
根据系统函数的定义,得系统的系统函数为
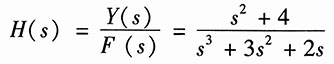
(4)由图(d),可得输出的象函数为
Y(s)=F(s)+e
-TsY(s)
解得
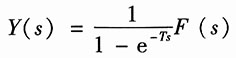
根据系统函数的定义,得系统的系统函数为

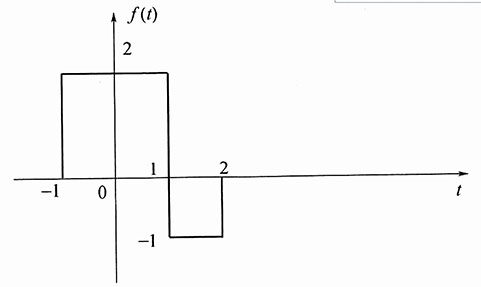
2. f(t)=2ε(t+1)-3ε(t-1)+ε(t-2)
3. f(t)=r(t)-2r(t-1)+r(t-2)
解:

该信号波形如图所示。
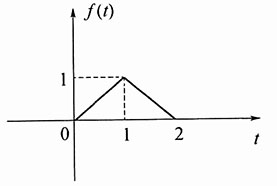
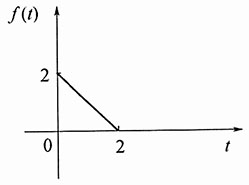
4. f(t)=ε(t)γ(2-t)
解:
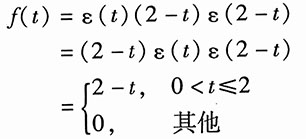
该信号波形如图所示。
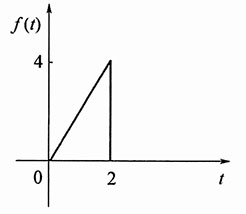
5. f(t)=r(2t)ε(2-t)
解:
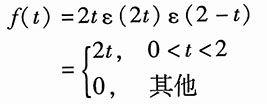
该信号波形如图所示。
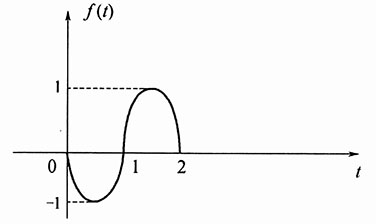
6. f(t)=sin(πt)[ε(t)-ε(t-1)]
解:f(t)=sin(πt)[ε(t)-ε(t-1)]
该信号波形如图所示。
7. f(t)=sin[π(t-1)][ε(t)-ε(t-1)]
11.
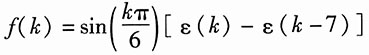
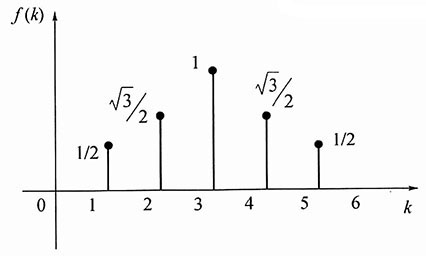
12. f(k)=2
k[ε(3-k)-ε(-k)]
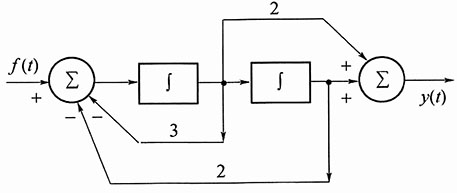
13. 如图所示的系统,试求输入f(t)=ε(t)时,系统的零状态响应。
解:先求得系统的冲激响应。设右端积分器的输出为x(t),则由左端加法器输出,得
x"(t)=f(t)-3x'(t)-2x(t)
即
x"(t)+3x'(t)+2x(t)=f(t) (1)
由右端加法器的输出,得
y(t)=x(t)+2x'(t) (2)
设式(1)的冲激响应为h
1(t),即满足
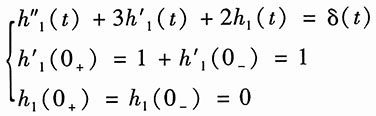
解此方程,得
h
1(t)=c
1e
-tε(t)+c
2e
-2tε(t)
将初始条件代入上式,解得c
1=1,c
2=-1,所以
h
1(t)=(e
-t-e
-2t)ε(t)
由式(2)知系统的冲激响应为
h(t)=h
1(t)+2h'
1(t)
=(3e
-2t-e
-t)ε(t)
所以当输入f(t)=ε(t)时,有
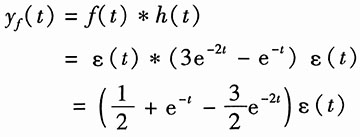
14. a
0=2,a
1=3;
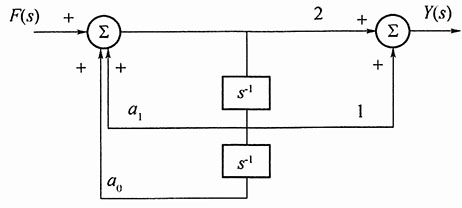
解:设图中左边加法器的输出为X(s),则可列出方程:
X(s)=a
1s
-1X(s)+a
0s
-2X(s)+F(s)
Y(s)=2X(s)+s
-2X(s)
由以上两式,消去中间变量X(s),可得系统函数为
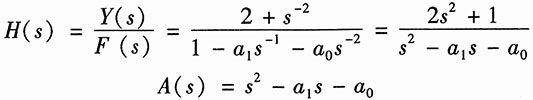
当a
0=2,a
1=3时,A(s)=s
2-3s-2=0。
极点为
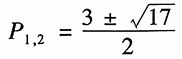
可见,其极点不全部在左半开平面,故系统不稳定。
15. a
0=-2,a
1=-3;
解:当a0=2,a1=-3时,A(s)=s2+3s+2=0。
极点为p1=-1,p2=-2,可见,其极点全部在左半开平面,故系统稳定。
16. a
0=2,a
1=-3。
解:当a
0=2,a
1=-3时,A(s)=s
2+3s-2=0。
极点为
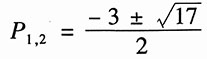
可见,其极点不全部在左半开平面,故系统不稳定。
17. 求图1所示各信号的傅里叶变换。

图1
18. 依据上题第一小题、第二小题的结果,利用傅里叶变换的性质,求图2所示各信号的傅里叶变换。
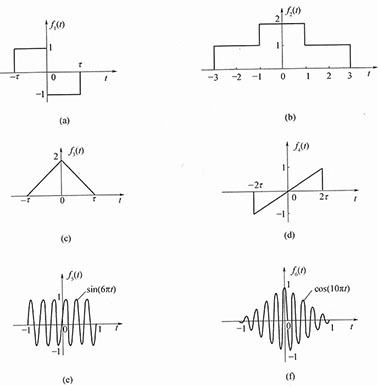
图2
解:设图1(a)的信号为f
a(t),(b)的信号为f
b(t)。
(1)由图2(a)知f
1(t)=f
a(-t)-f
a(t)。
因为

所以
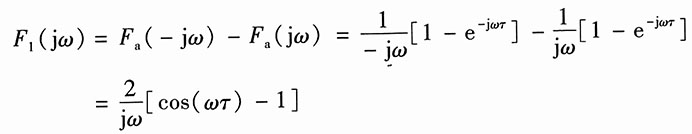
(2)由图2(b)得
f
a(t)=[f
a(t)+f
a(-t)](τ=3)+[f
a(-t)+f
a(t)](τ=1)
所以
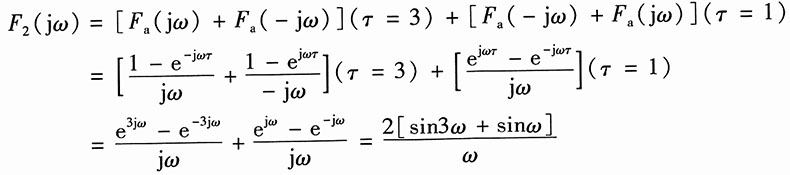
(3)由图2(c):
f
3(t)=[2-2f
b(t)][ε(t)-ε(t-2)]+[2-2f
b(-t)][ε(t+2)-ε(t)]
=2[ε(t+2)-ε(t-2)]-2f
b(t)-f
b(-t)
因为
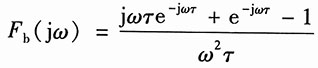
所以
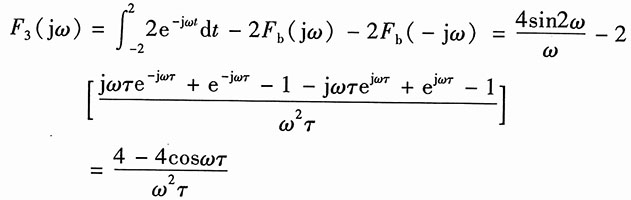
(4)令
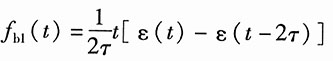
则由第二小题知
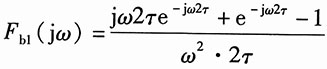
。
由图2(d)知
f
4(t)=f
b1(t)-f
b1(-t)
所以
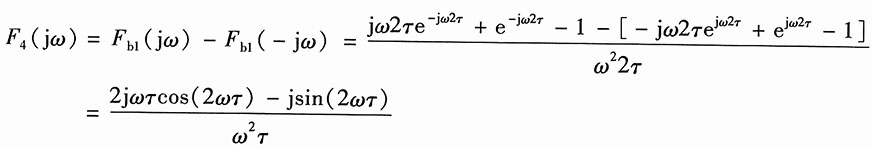
(5)f
5(t)=sin(6πt)[ε(t+1)-ε(t-1)]
所以
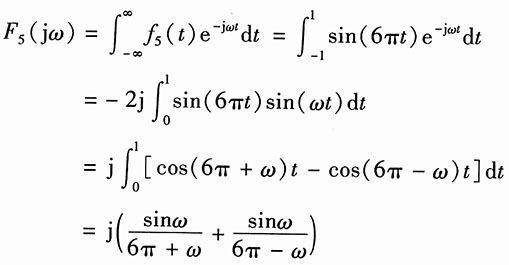
(6)由图2(c):
令

则
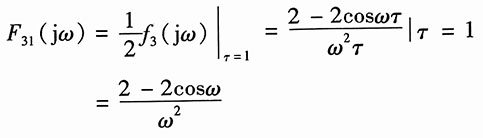
由图2(t)可以看出
f
b(t)=f
31(t)·cos(10πt)
因为
F[cos(10πt)]=π[δ(ω-10π)+δ(ω+10π)]
所以
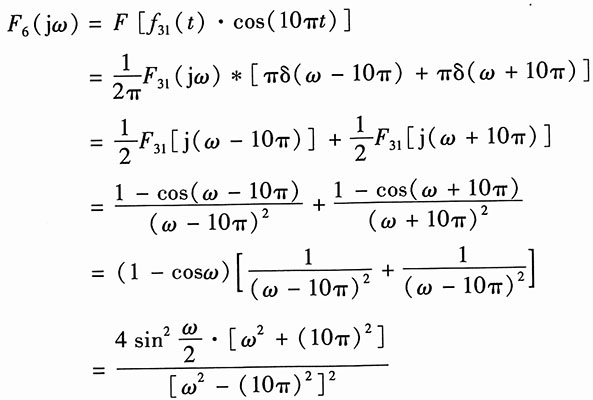
19. y(k)+3y(k-1)+2y(k-2)=f(k)
y(-1)=0,y(-2)=1;
解:
由已知可得
yx(k)+3yx(k-1)+2yx(k-2)=0 (1)
因为
yx(-1)=y(-1)=0
yx(-2)=y(-2)=1
由式(1)可得
yx(0)=-3yx(-1)-2yx(-2)=-2
yx(1)=-3yx(0)-2yx(-1)=6
特征方程为
λ2+3λ+2=0
所以特征根为
λ1=-1,λ2=-2
yx(k)=[c1(-1)k+c2(-2)k]ε(k)
将yx(+1)=6,yx(0)=-2代入上式,解得c1=2,c2=-4,所以
yx(k)=[2(-1)k-4(-2)k]ε(k)
20. y(k)+2y(k-1)+y(k-2)=f(k)-f(k-1)
y(-1)=1,y(-2)=-3;
解:由已知差分方程可得
yx(k)+2yx(k-1)+yx(k-2)=0 (2)
因为
yx(-1)=y(-1)=1,yx(-2)=y(-2)=-3
所以由式(2)可得
yx(0)=-2yx(-1)-yx(-2)=1
yx(1)=-2yx(0)-yx(-1)=-3
由式(2)可得特征根为λ1=λ2=-1,所以
yx(k)=[(c1k+c2)(-1)k]ε(k)
将yx(0)、yx(1)代入上式,可解得c1=2,c2=1,所以
yx(k)=[(2k+1)(-1)k]ε(k)
21. y(k)+y(k-2)=f(k-2)
y(-1)=-2,y(-2)=-1。
解:由已知差分方程可得
y
x(k)+y
x(k-2)=0 (3)
由式(3)可得
y
x(0)=-y
x(-2)=-y(-2)=+1
y
x(1)=-y
x(-1)=-y(-1)=2
由已知差分方程可知特征方程为λ
2+1=0,所以

将y
x(0)=1,y
x(1)=2代入上式,可得c
1=1,c
2=1,所以
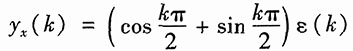
22. 系统函数
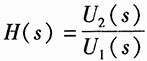
解:画出题中电路的零状态s域电路模型(图2)。
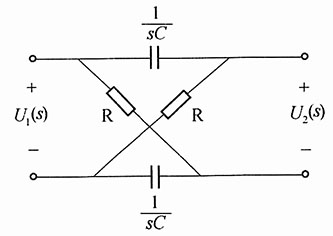
图2
借助分压公式,容易得出
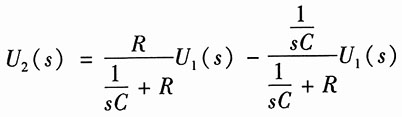
于是可解得系统函数为
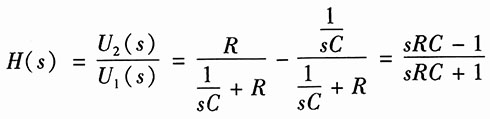
将R、C的数值代入,得
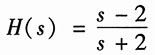
23. 冲激响应和阶跃响应;
解:取H(s)的逆变换得系统的冲激响应为
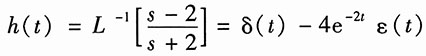
系统阶跃响应的象函数为
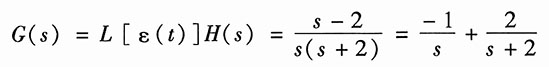
取逆变换,可得系统的阶跃响应为
g(t)=(-1+2e
-2t)ε(t)
24. 输入为图1(b)所示的矩形脉冲时的零状态响应y
zs(t);
解:由u
1(t)的波形,可写出其表达式
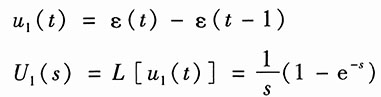
则系统零状态响应的象函数为

取逆变换,得系统的零状态响应为
y
zs(t)=(2e
-2t-1)ε(t)-(2e
-2(t-1)-1)ε(t-1)
25. 输入为图2(c)所示的锯齿波时的零状态响应y
zs(t)。
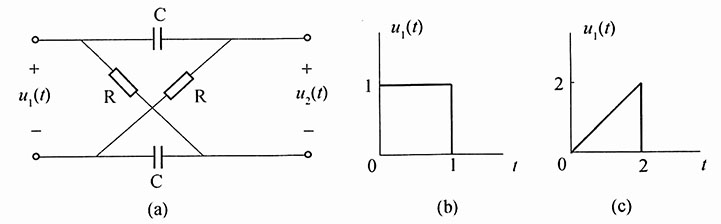
图1
解:由u
1(t)的波形,可写出其表达式为

则系统零状态响应的象函数为
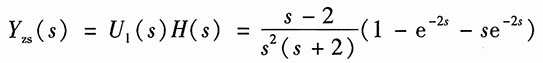
取逆变换,得系统的零状态响应为
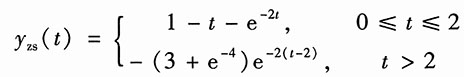
26.
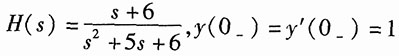
解:由于系统函数H(s)可知系统方程的特征根为s1=-2,s2=-3,故系统的零输入响应为
yzi(t)=C1e-2t+C2e-3t
代入y(0-)=y'(0-)=1,得
y(0-)=C1+C2=1
y'(0-)=-2C1-3C2=1
解得C1=4,C2=-3,因此,得
yzi(t)=4e-2t-3e-3t,t≥0
27.
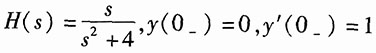
解:由
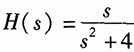
写出描述系统的微分方程为
y"(t)+4y(t)=f'(t)
对微分方程两边取拉普拉斯变换,利用微分特性,得
s
2Y(s)-sy(0
-)-y'(0
-)+4Y(s)=sF(s)
解得
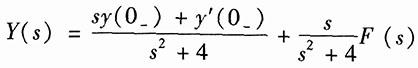
将y(0
-)=0,y'(0
-)=1代入,得零输入响应的象函数:

取逆变换,得系统的零输入响应为
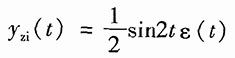
28.
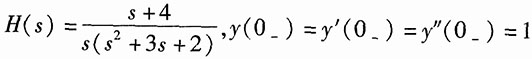
解:由
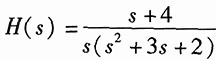
写出描述系统的微分方程:
y"'(t)+3y"(t)+2y'(t)=f'(t)+4f(t)
对微分方程两边取拉普拉斯变换,利用微分特性,得
s
3Y(s)-s
2y(0
-)-sy'(0
-)-y"(0
-)+3s
2Y(s)-3sy(0
-)-
3sy'(0-)+2sY(s)-2y(0
-)=sF(s)+4F(s)
解得

将y(0
-)=y'(0
-)=y''(0
-)=1代入,得零输入响应的象函数:
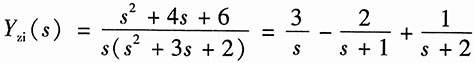
取逆变换,得系统的零输入响应为
y
zi(t)=(3-3e
-t+e
-2t)ε(t)
29. 有限频带信号f(t)=5+2cos(2πf
1t)+cos(4πf
1t),其中f
1=1kHz,用f
s=5kHz的冲激函数序列δ
Ts(t)进行取样。
(1)画出f(t)及取样信号f
s(t)在频率区间(-10kHz,10kHz)的频谱图。
(2)若由f
s(t)恢复原信号,理想低通滤波器的截止频率f
c应如何选择。
解:(1)F(jω)=10πδ(ω)+2π[δ(ω+ω
1)+δ(ω-ω
1)]+π[δ(ω+2ω
1)+δ(ω-2ω
1)],ω
1=2πf
1 冲激函数序列δ
Ts(t)的频谱函数为
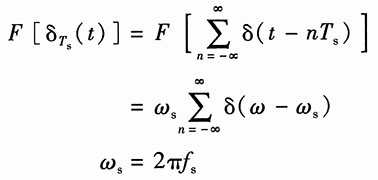
所以
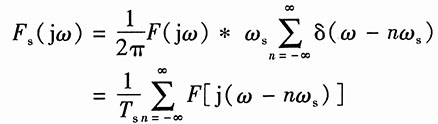
由F(jω)、F
s(jω)可以画出其在(-10kHz,10kHz)的频谱图(图1和图2):
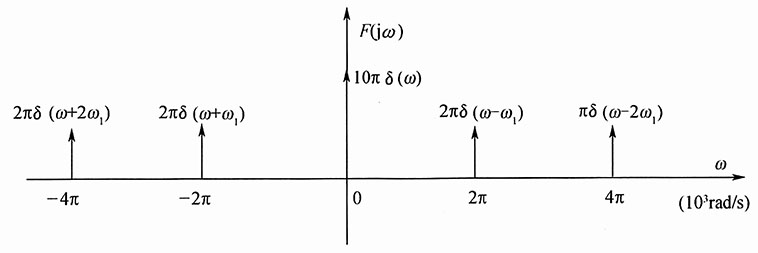
图1
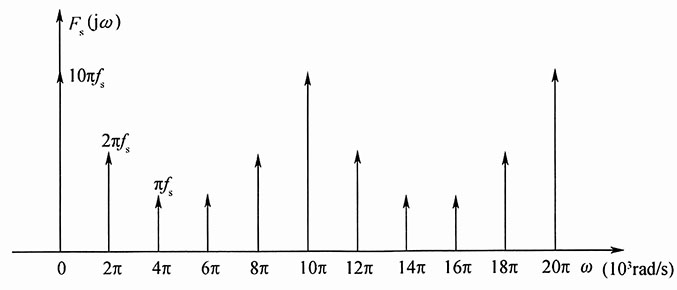
图2
F
s(jω)负半轴和正半轴是对称的,略。
(2)由F(jω)看出其ω
m=2ω
1,所以
ω
m<ω
c<ω
s-ω
m 即
4πf
1<2πf
c<2πf
2-4πf
1 2f
1<f
c<f
2-2f
1 即
2kHz<f
c<3kHz
30. 有限频带信号f(t)=5+2cos(2πf
1t)+cos(4πf
1t),其中f
1=1kHz,用f
s=800Hz的冲激函数序列δ
Ts(t)进行取样(请注意f
s<f
1)。
(1)画出f(t)及取样信号f
s(t)在频率区间(-2kHz,2kHz)的频谱图。
(2)若将取样信号f
s(t)输入到截止频率f
c=500Hz,幅度为T的理想低通滤波器,即其频率响应为
画出滤波器的输出信号的频谱,并求出输出信号y(t)。
解:(1)由题知
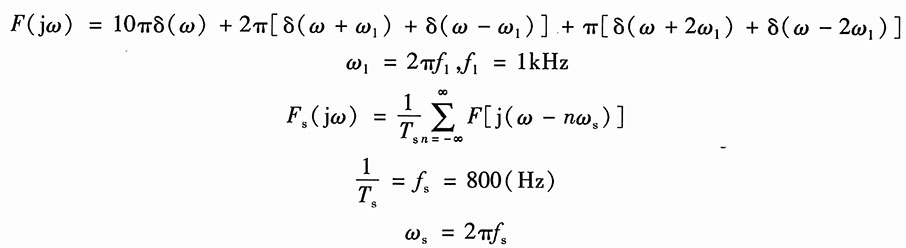
因此,可画出f(t)及取样信号f
s(t)在频率区间(-2kHz,2kHz)的频谱图,分别如图3(a)、(b)所示。
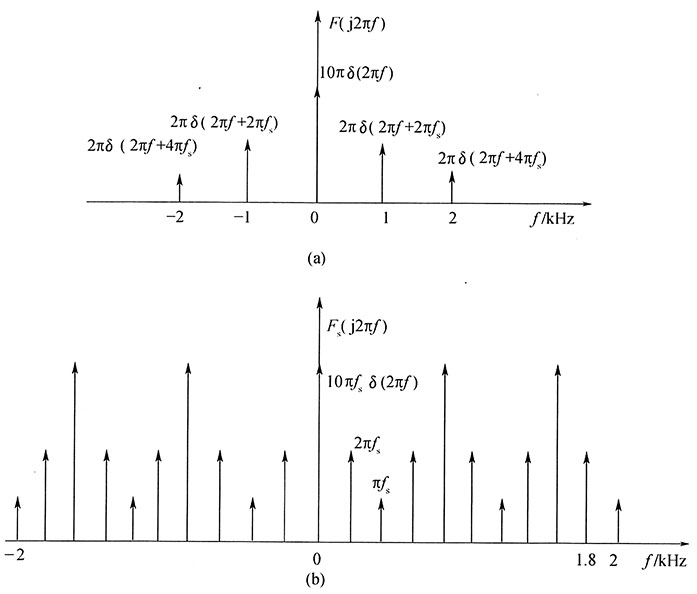
图3
(2)可将理想低通滤波器的频率响应H(j2πf)写为
H(j2πf)=T
sgf
1(j2πf)
则借助图2(b),可得输出信号的频谱为
Y(j2πf)=F
s(j2πf)H(j2πf)=F
s(j2πf)T
sgf
1(j2πf)
=10πδ(2πf)+2π[δ(2πf+2π×0.2f
1)+δ(2πf-2π×0.2f
1)]+
π[δ(2πf)+4π×0.4f
1)+δ(2πf-4π×0.4f
1)]
其频谱图如图4所示,则低通滤波器的输出为
y(t)=F
-1[Y(j2πf)]=5+2cos(2π×0.2f
1t)+cos(2π×0.4f
1t)
=5+2cos400πt+cos800πt
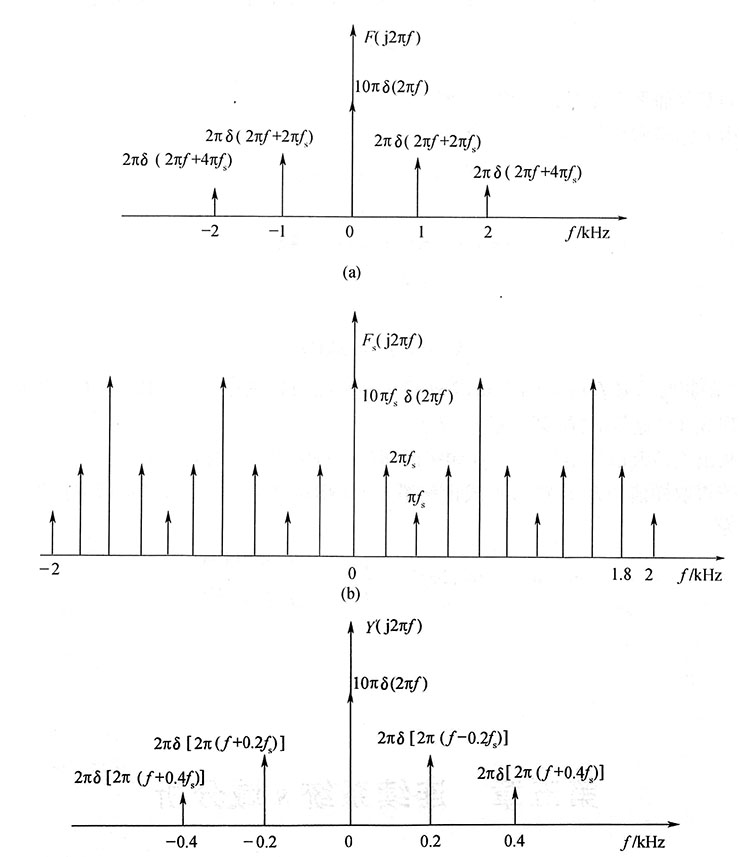
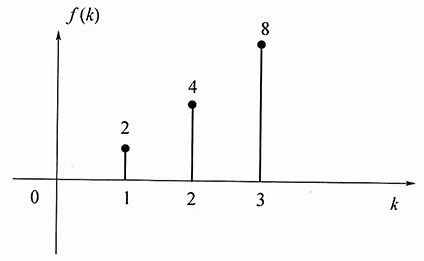
31. 图1所示为用横向滤波器实现的时域均衡器,要求当输入
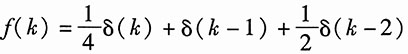
时,其零状态响应y
zs(k)中y
zs(0)=1,y
zs(1)=y
zs(3)=0,试确定系数a、b、c的值。
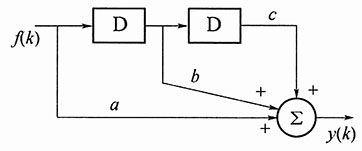
图1
解:由加法器输出可列出方程:
Y
zs(z)=aF(z)+bz
-1F(z)+cz
-2F(z)=(a+bz
-1+cz
-2)F(z)=H(z)F(z)
式中系统函数为
H(z)=(a+bz
-1+cz
-2)
又由已知
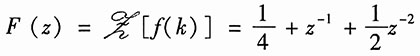
则系统零状态响应的象函数为
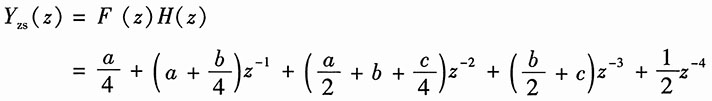
对上式取逆变换,得系统的零状态响应为
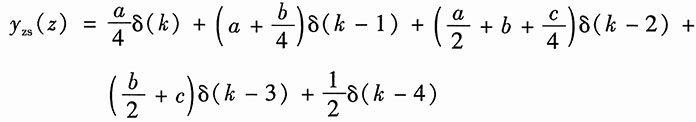
则可得
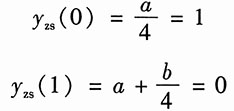

由以上三式可解得a=4,b=-16,c=8。
其图形如图2所示。

图2
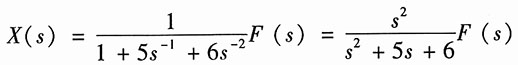 (1)
(1)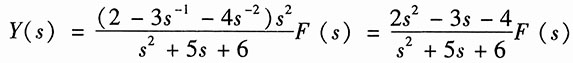
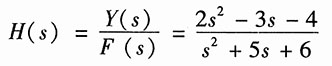
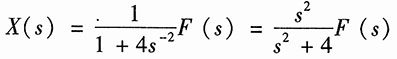 (2)
(2)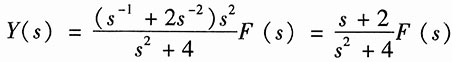
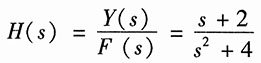
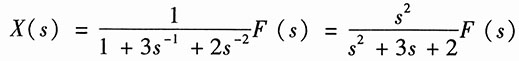 (3)
(3)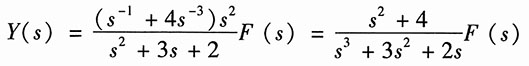
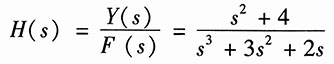
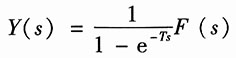


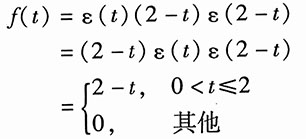
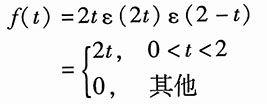
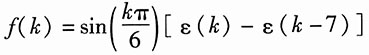
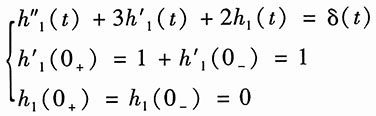
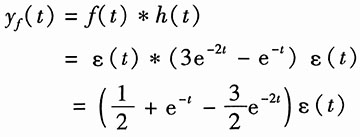
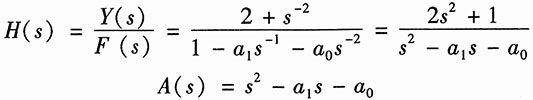
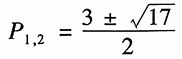
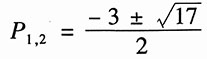

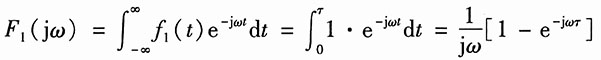
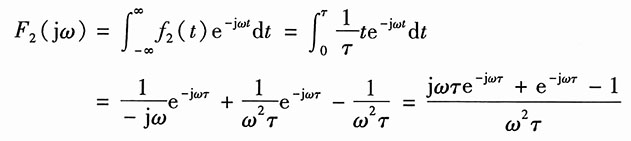
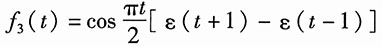
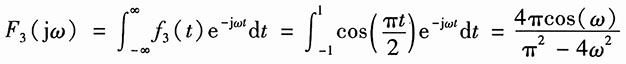
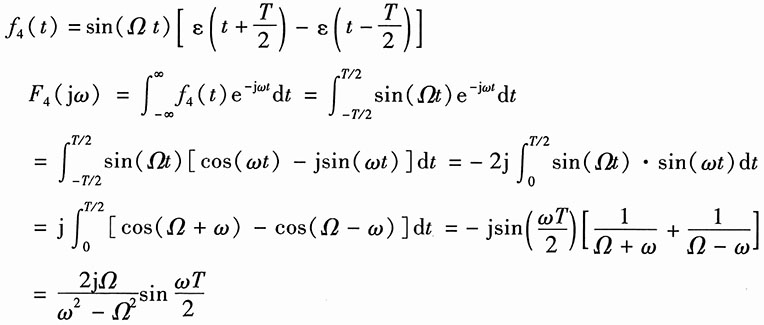


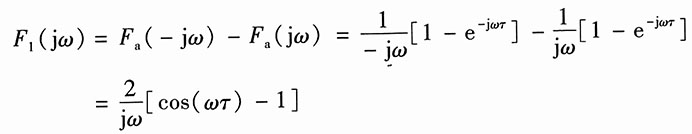
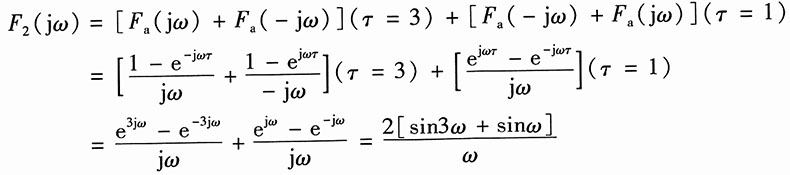
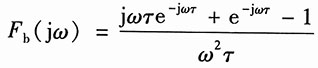
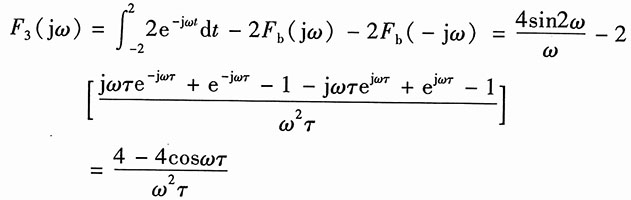
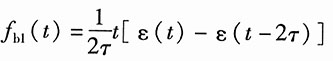
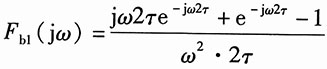 。
。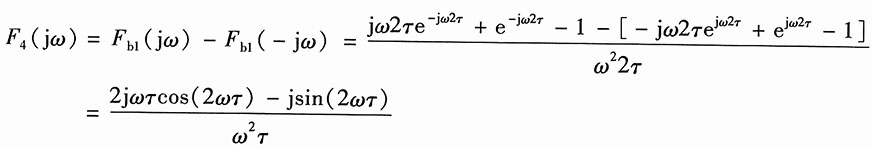
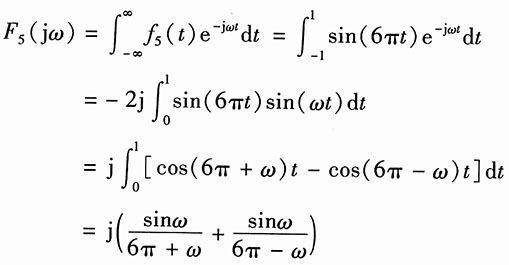

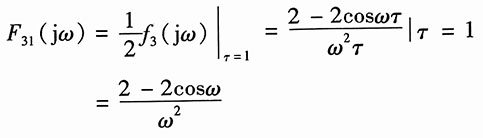
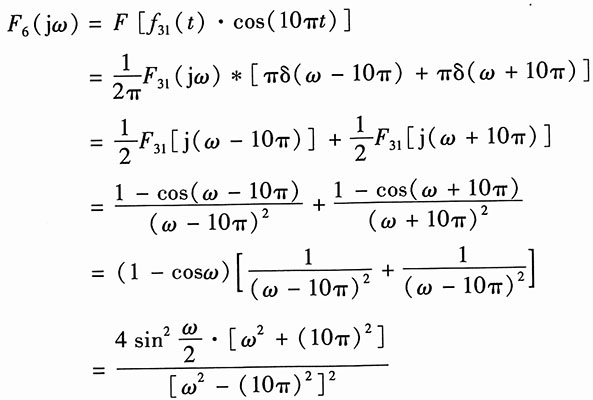

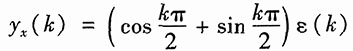
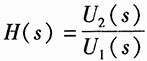

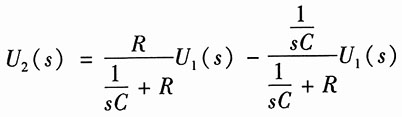
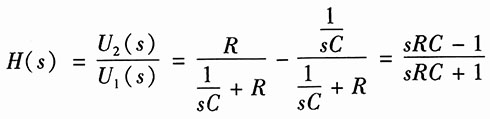
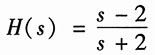
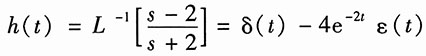
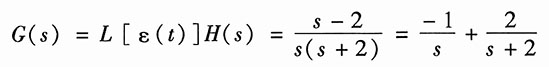
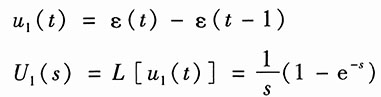



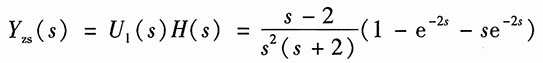
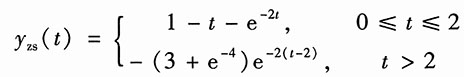
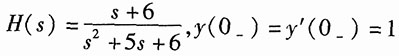
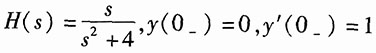
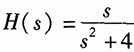 写出描述系统的微分方程为
写出描述系统的微分方程为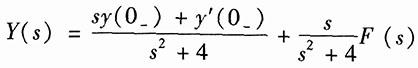

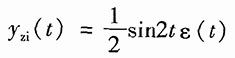
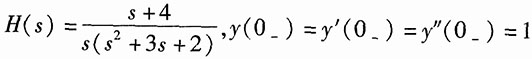
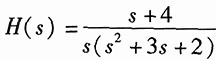 写出描述系统的微分方程:
写出描述系统的微分方程:
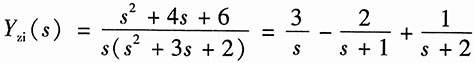
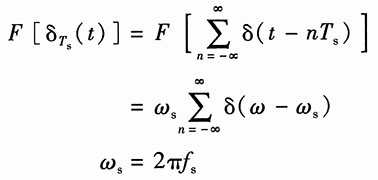
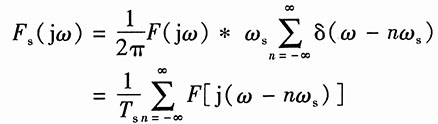


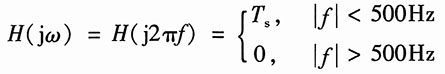
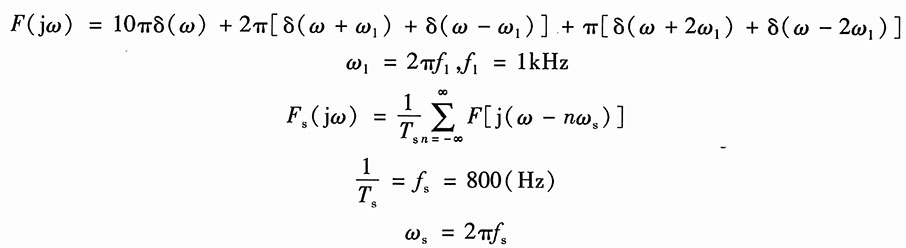


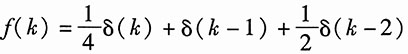 时,其零状态响应yzs(k)中yzs(0)=1,yzs(1)=yzs(3)=0,试确定系数a、b、c的值。
时,其零状态响应yzs(k)中yzs(0)=1,yzs(1)=yzs(3)=0,试确定系数a、b、c的值。