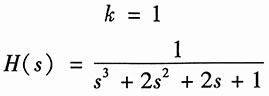计算题1. 如图为有源电路。试用罗斯—霍尔维兹准则确定为使系统稳定,K应满足什么条件?
解:(1)设从左边第一节点电压为u
a,第二个节点为u
b,则由图(a)列写方程:
u
1(s)+u
2(s)=u
0(s) (1)
对结点a:

(2)
结点b:
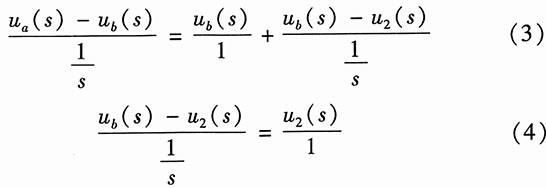
将以上四个方程联立解得系统函数为

所以系统的特征多项式为
A(s)=(k+1)s
3+6s
2+5s+1
A(s)系数排成罗斯阵列为
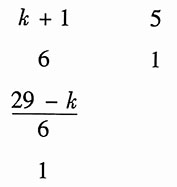
若系统是稳定的,根据罗斯准则,以上阵列中第一项元素应全为正值,所以要求:
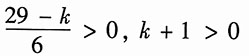
即-1<k<29,实际物理系统中系数k大于零。
因此,取0<k<29即在此范围时,系统是稳定的。
(2)设中间结点电压为u
a(s),由图(b)列写方程:
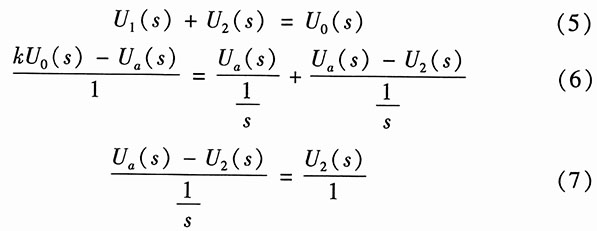
将以上三个方程联立解得系统函数为
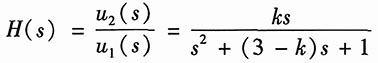
所以系统的特征多项式为
A(s)=s
2+(3-k)s+1
将A(s)系数排成罗斯阵列:
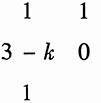
若系统稳定,则根据罗斯准则,以上阵列中的第一列元素应全为正值。即要求:3-k>0
k<3,实际系统中的系数为正值,即0<k<3时,系统是稳定的。
2. 下图所示电路的输入阻抗函数
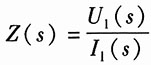
的零点在-2,极点在
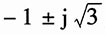
,且
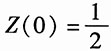
。求R、L、C的值。
解:由已知电路可得输入阻抗函数为
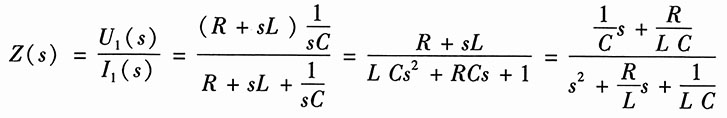
(1)
再根据题中已知输入阻抗函数的零极点,可得
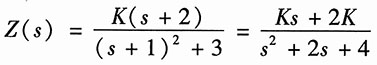
由于Z(0)=1/2,则有
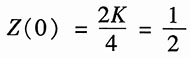
故K=1。因此
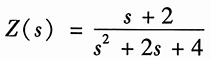
(2)
比较式(1)和式(2)的系数,可得
R=0.5Ω,L=0.25H,C=1F
3. 设a、b为常数(a≠0),试证明:
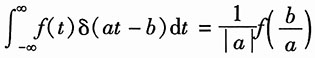
(提示:先证a>0再证a<0)。
证明:令u=at-b,a≠0,所以
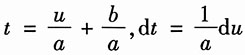
。
(1)a>0
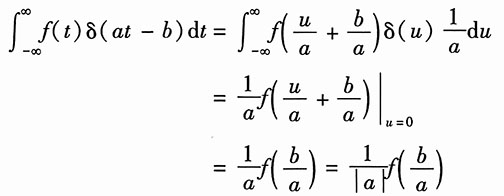
(2)同理可以得a<0时等式也成立。
证毕。
4. 求图中信号流图的增益
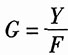
的值。
解:(1)图(a)中,有两个回路,回路增益分别为
L
1=1×2×2=4
L
2=2×3×0.5=3
并且该两个回路相接触,所以信号流图的特征多项式为
Δ=1-L
1-L
2=1-4-3=-6
它有一条前向通路,其增益为
P
1=2×1×2×3×1=12
由于该前向通路与回路相接触,则其特征余子式为
Δ
1=1
利用梅森公式,可得该信号流图的增益为
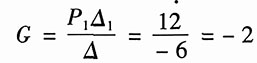
(2)图(b)中,有两个回路,回路增益分别为
L
1=2×2=4
L
2=1×3=3
并且该两个回路相接触,所以信号流图的特征多项式为
Δ=1-L
1-L
2=1-4-3=-6
它有两条前向通路,其增益分别为
P
1=1×2×3×1=6
P
2=1×2×1=2
并知前向通路P
1与回路L
1接触,与回路L
2不接触,于是P
1特征余子式为
Δ
1=1-L
2=1-3=-2
前向通路P
2与回路L
1和回路L
2均不接触,于是P
2特征余子式为
Δ
2=1-L
1-L
2=1-4-3=-6
利用梅森公式,可得该信号流图的增益为
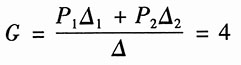
5. 如图所示的系统,试求当输入f(t)=ε(t)-ε(t-4π)时,系统的零状态响应。
解:设右端的积分器输出为x(t),则由加法四则输出,得
x"(t)=f(t)-x(t)
即
x"(t)+x(t)=f(t) (1)
左端积分输出为
y(t)=x'(t) (2)
设式(1)的冲激响应为h
1(t)中,即
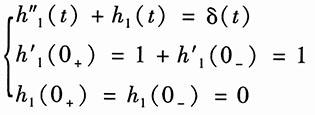
解此方程得
h
1(t)=(c
1cost+c
2sint)·ε(t)
将初始条件代入,解得c
1=0,c
2=1,即
h
1(t)=sint·ε(t)
所以由式(2)可知系统的冲激响应为
h(t)=h'
1(t)
=[sint·ε(t)]'=cosε(t)·ε(t)
所以当f(t)=ε(t)-ε(t-4π)时,有
y(t)=f(t)*h(t)
=[ε(t)-ε(t-4π)]*cost·ε(t)
=[δ(t)-δ(t-4π)]*ε(t)*cost·ε(t)
=[δ(t)-δ(t-4π)]*[sint·ε(t)]
=sint·ε(t)-sin[(t-4π)]·ε(t-4π)
=sint·[ε(t)-ε(t-4π)]
6. 如图1的RC带通滤波电路,求其电压比函数
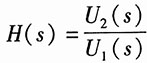
及其零极点。
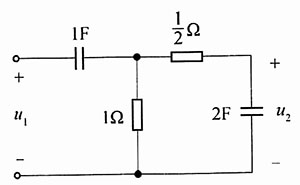
图1
解:画出零状态s域等效电路模型(图2)。
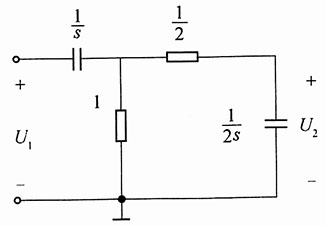
图2
设1Ω电阻的电压为U
a(s),则列出该点的结点方程为
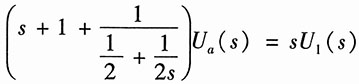
解得

利用分压公式,得
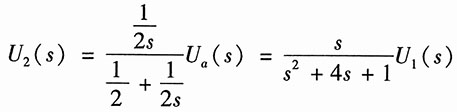
由此可得系统函数为
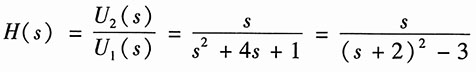
故零点和极点分别为
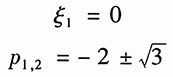
7. 试画出图所示信号的奇分量和偶分量。
解:提示,奇分量为
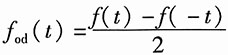
,偶分量为
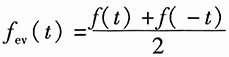
,据此可以画出两个图形的奇偶分量图形。图略。
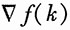 与求和
与求和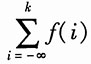 。
。
9.
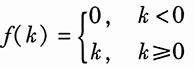
解:f(k)=kε(k)
所以
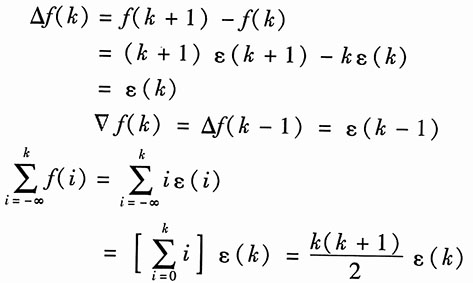
10. 如图的电路,若以u
S(t)为输入,u
C(t)为输出,试列出其微分方程,求出其冲激响应和阶跃响应。
解:由电路图可列写下列方程:
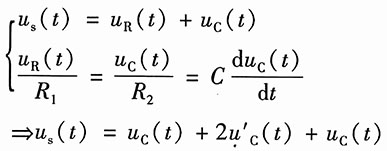
即
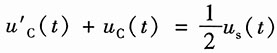
(1)
设式(1)冲激响应为h(t),则
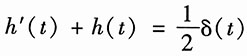
(2)
由式(2)知
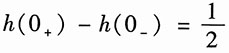
所以
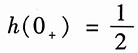
式(1)的解为h(t)=c
1e
-tε(t),将h(0
+)代入,得
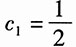
,所以
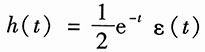
所以其阶跃响应为
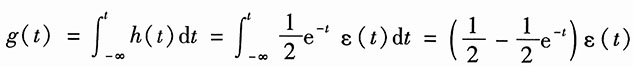
11. 零点在0、-2±j1,极点在-3、-1±j3且H(-2)=-1;
解:由题中已知的零点和极点,可得系统函数为

由于H(-2)=-1,因此有
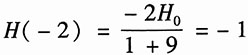
解得H
0=5,故
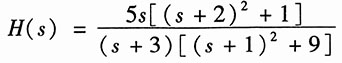
12. 零点在0、±j3,极点在±j2、±j4,且当s=j1时,
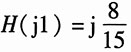
;
解:由题中已知的零点和极点,可得系统函数为
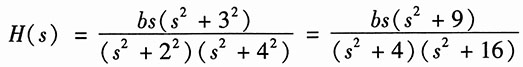
将
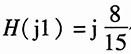
代入得
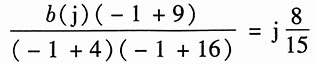
所以
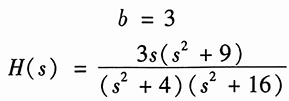
13. 零点在2±j1,极点在-2±j1,且H(0)=2;
解:由题中已知的零点和极点,可得系统函数为
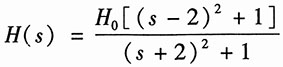
由于H(0)=2,因此有
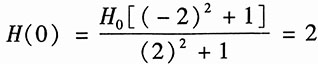
解得H
0=2,故
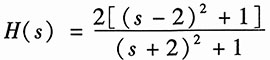
14. 极点在-1,e
±j120°,且H(0)=1。
解:由已知设系统函数
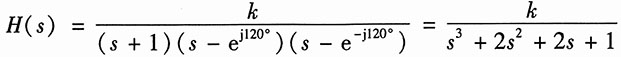
又因为H(0)=1,所以