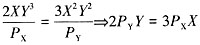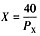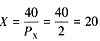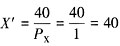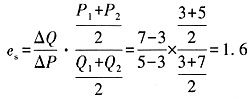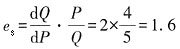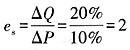计算题1. 某人向A、B两保险公司投保。A保险公司保额20万元,B保险公司保额40万元,损失30万元。求三种情况下的(比例分摊方式、限额责任分摊方式、顺序责任分摊方式)重复保险分摊。
(1)比例责任分摊方式是以各保险人所承保的保险金额为基础来计算分摊责任的方式.即按照各保险人所承保的保险金额与各保险人所承保的保险金额总和的比例来分摊损失赔偿责任的方式,计算公式为:
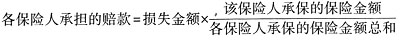
带入数据可得:
A公司应分摊:
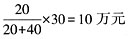
B公司应分摊:
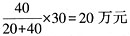
(2)限额责任分摊方式是以各保险人在保险事故损失中的赔偿限额为基础来计算分摊责任的方式,即假设在没有重复保险的条件下,各保险人依其承保的保险金额应负责赔偿的最高限额与各保险人应负赔偿限额总和的比例分摊责任的方式。计算公式为:

带入数据可得:
A公司应分摊:
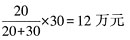
B公司应分摊:
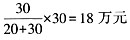
(3)顺序责任分摊方式是以各保险人签发保险单的时间顺序为基础来计算分摊责任的方式。首先由最早出单的保险公司在其保险金额范围内先行赔付,如果应赔偿的总金额超过第一家保险公司的保险金额,则由第二家保险公司在其保险金额范围内赔付超出部分,以此顺序类推,但赔偿责任以所有保险人的保险总金额为限。
则A公司应分摊20万元,B公司应分摊10万元。
2. 某年物价指数为97,银行一年期利率为1.08%,实际利率是多少?
解:物价指数为97,意味着按报告期计算的物价水平总和是按基期价格水平计算的物价水平的97%。由于通货膨胀率为物价水平的上升速度,可得通货膨胀率为-3%。
根据公式利率r*=[(1+r)/(1+p)-1]×100%,其中r为名义利率,p为通货膨胀率。在本题中,r=1.08%,p=-3%,代入可知r*=(1+1.08%)/(1-3%)-1=4.21%。
[考点] 利息率的定文、种类和作用
6. 求均衡价格,均衡交易量和此时的需求价格弹性;
当供给等于需求时,市场上的价格称为均衡价格,此时的交易量称为均衡交易量。联立求解需求函数和供给函数
Q=400-P
Q=P+100
可得均衡价格P=150元,均衡交易量Q为250。
根据需求价格弹性公式.此时的需求价格弹性为:
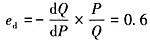
7. 若政府在消费者购买该商品时对每单位商品征收10元的消费税,求新的均衡价格。均衡交易量和相应的需求价格弹性。
若政府在消费者购买该商品时对每单位商品征收10元的消费税,则供给函数为:
Q=(P-10)+100=P+90
需求函数不变,解得此时的均衡价格P=155元,均衡交易量Q为245,此时的需求价格弹性为:
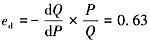
8. 小王今年20岁,购买一份保险,约定如果他能活到60岁,则从保险公司得到10万元一次性给付。设年利率为6%,l
20=983992,l
40=966271,l
60=877671,求这笔钱给付在小王20岁时的现值。
小王可以活到60岁的概率为
40P
20,他在60岁获得这笔钱给付的期望值为
100000×
40P
20+0×(1-
40P
20)=100000×
40P
20 这笔给付在小王20岁时的现值通过利率折现得到:
100000×
40P
20×(1+6%)
-40 
所以,这笔现值为100000×0.89195×1.06
-40=86.72元。
9. 已知生产函数Q=f(K,L)=KL-0.5L
2-0.32K
2,Q表示产量,K表示资本,L表示劳动。令上式K=10。
(1)写出劳动的平均产量函数和边际产量函数。
(2)分别计算当总产量、平均产量和边际产量达到极大值时,厂商雇用的劳动。
(3)证明当AP
L达到极大时,AP
L=MP
L=2。
解:(1)把K=10代入生产函数可以得到:Q=f(K,L)=10L一0.5L
2-32
劳动的平均产量函数为
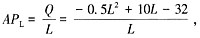
边际产量函数为:
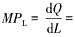
-L+10
(2)当
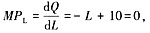
即L=10时,总产量最大。
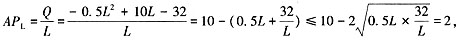
其中0.5L=
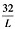
,即L=8时,平均产量最大。由边际产量函数可以知道,当L=0时,边际产量最大。
(3)由(2)可以知道,当L=8时,平均产量最大,且AP
L=2。把L=8代入边际产量函数,可以得到MP
L=-8+10=2。
[考点] 总产品、平均产品与边际产品,生产的三阶段论
10. 他将选择每周工作多少小时?
假设工人的工资率为w,商品x和y的价格分别为P
x和P
y,每周的总收入为(24×7-L)w=168w-Lw。
因此,张三的效用最大化问题为:
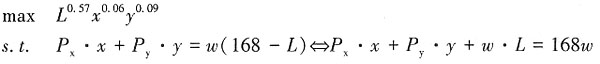
利用拉格朗日乘数法可以解得:
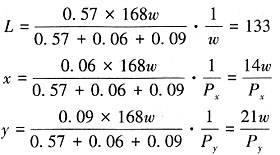
因此,该工人每周工作的时间为:168-L=168-133=35(小时)
11. 他将把收入的多大比例用于购买x?
该工人每周的总收入为:
(168-L)w=35w
所以,该消费者用于x的商品的支出比例为:
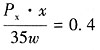
12. 他消费x的需求价格弹性。
消费x的需求价格弹性为:
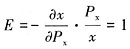
13. 如果他的收入下降30%,Y的价格下降50%,他将过得更好还是更坏?
原先消费者的效用为:
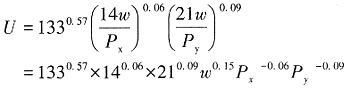
由(1)可知,收入增加、商品y的价格变化不会改变张三的工作与休闲的时间。收入下降30%主要表现为工资率减少30%。
因此,当收入下降30%,Y的价格下降50%时,张三的效用为:
U'=133
0.57×14
0.06×21
0.09(0.7w)
0.15P
x-
0.06(0.5P
y)
-0.09 因为0.7
0.150.5
-0.09>1,所以,U'>U,因而消费者将过得更好。
14. 某商业银行体系持有准备金300亿元,公众持有通货100亿元,中央银行对活期存款和非个人定期存款规定的法定准备率分别为15%和10%,据测算,流通中现金漏损率为25%,商业银行超额准备率为5%,非个人定期存款比率为50%,试求:
①活期存款乘数:
②货币乘数:
③狭义货币供给量M
1。
解:①活期存款乘数
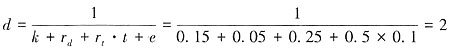
②货币乘数
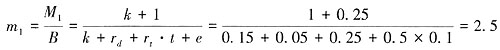
③货币供给量M
1=B·m
1=(R+C)·m
1=(300+100)×2.5=1000亿元
[考点] 基础货币与货币乘数
15. 已知生产函数Q=A
1/4L
1/4K
1/2,各要素价格为P
A=1,P
L=1,P
K=2,求厂商的总成本函数。
解:根据成本函数的定义,成本函数是指生产既定产量的最小成本,假设要生产产量为Q,则约束条件为Q=A
1/4L
1/4K
1/2,在此条件下求C=AP
A+LP
L+KP
K的最小值,构造Lagrange函数。
F(A,L,K,λ)=AP
A+LP
L+KP
K+λ(A
1/4L
1/4K
1/4-Q),令各偏导数等于0。
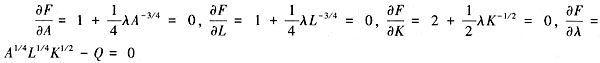
整理得A=L=Q
4/5,K=Q
6/5,所以成本函数为C=2Q
4/5+2Q
6/5。
[考点] 短期成本函数与短期成本曲线
16. 求对商品X的需求函数。
设商品X,Y的价格分别为P
X,P
Y,根据消费者均衡条件
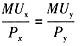
,得:
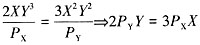
再结合约束条件M=P
XX+P
YY=100,可求得商品X的需求函数为:
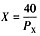
17. 设商品Y的价格P
Y=3,商品X的价格P
X从2降为1,求替代效应和收入效应。
当P
Y=3,P
X=2时,根据上面求得的需求函数消费者均衡条件我们可以得到商品X的最优消费量为:
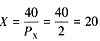
将数据代入到预算约束中便得到商品Y的最优消费量为:
Y=(100-P
XX)/P
Y=60/3=20
因此消费者的效用为U(X,Y)=X
2Y
3=20
5。
当商品x的价格P
X从2降为1时,根据上面求得的需求函数消费者均衡条件,我们可以得到商品X的新最优消费量为:
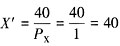
总的价格效应为(40-20)=20。
现在计算替代效应。
为保持原来的购买力不变,设在新价格体系下的新收入(补偿性收入)应为M',于是有:M'=P'
XX+P'
YY=20+60=80。
但是在新收入下消费者按照效用最大化去消费,于是设在新价格体系下消费者对两商品的最优消费量为X',Y',根据消费者均衡条件有:

此时的补偿预算线为:
M'=P'
XX'+P'
YY'==X'+3Y'=80
易得X'=32。
因此替代效应为(32-20)=12,收入效应为(40-32)=8。
18. 求出价格3和5之间的供给的价格弧弹性。
根据题意可知,P=3时,Q=3;P=5时,Q=7。
根据中点公式可得:
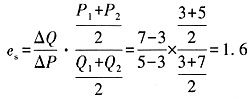
19. 根据给出的供给函数,求出P=4元是的供给的价格点弹性。
当P=4时,Q=-3+2×4=5,所以:
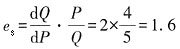
20. 若某商品的价格变动20%,其产量将变动10%,求这种商品的供给弹性。
根据商品供给弹性的定义,可知该商品的供给弹性为:
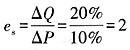
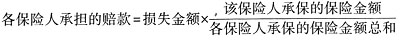
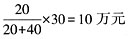
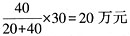

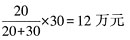
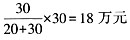
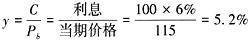


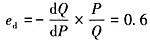
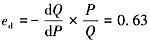

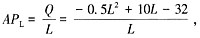 边际产量函数为:
边际产量函数为: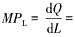 -L+10
-L+10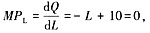 即L=10时,总产量最大。
即L=10时,总产量最大。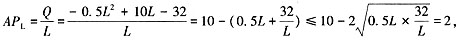 其中0.5L=
其中0.5L=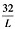 ,即L=8时,平均产量最大。由边际产量函数可以知道,当L=0时,边际产量最大。
,即L=8时,平均产量最大。由边际产量函数可以知道,当L=0时,边际产量最大。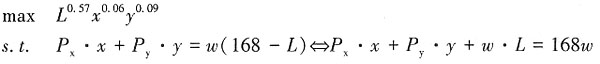
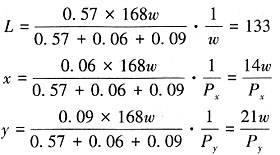
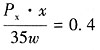
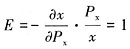
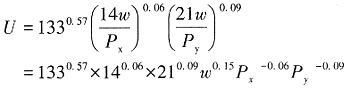
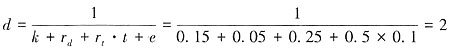
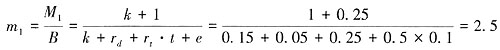
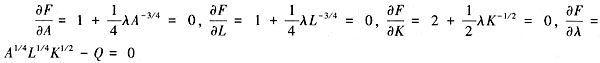
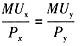 ,得:
,得: