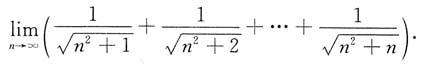一、单项选择题5. 若f(x+y,x-y)=x
2-y
2,则
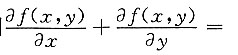
______
A B C D
C
[解析] f(x+y,x-y)=x
2-y
2=(x+y)(x-y),所以f(x,y)=xy,因此
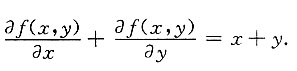
故选C.
6. 同时抛掷三枚匀称的硬币,正面与反面都出现的概率为______
A.
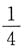
B.
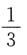
C.
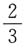
D.
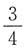
A B C D
D
[解析] 正面反面都出现,可以是一正二反或二正一反,
即
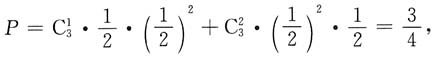
故应选D.
7. 若级数
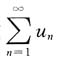
收敛,则下列级数中收敛的是______
A.
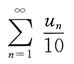
B.
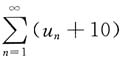
C.
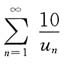
D.
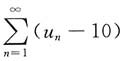
A B C D
A
[解析] 根据无穷级数的运算性质可以断定
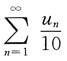
收敛,而其他选项均发散.故应选A.
8. 设函数f(x)在点x=1处可导,且
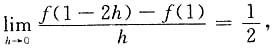
则f'(1)=______
A.
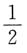
B.
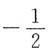
C.

D.
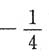
A B C D
D
[解析]
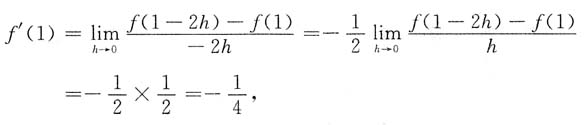
故应选D.
9. 由方程xy+lny=1确定的隐函数x=x(y)的微分dx______
A.
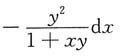
B.
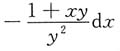
C.
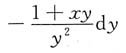
D.
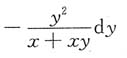
A B C D
C
[解析] 两边微分,得
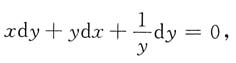
即(xy+1)dy+y
2dx=0,
所以
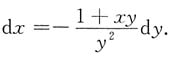
故应选C.
10. 设函数y=y(x)满足y=xlny,则
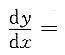
______
A.
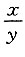
B.lny
C.
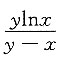
D.
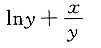
A B C D
C
[解析] 两边同时对x求导,得
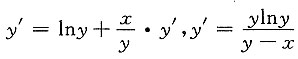
,故选C.
二、填空题1. 设D={(x,y)|x
2+y
2≤1},则
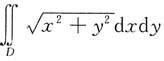
=______.
[解析]
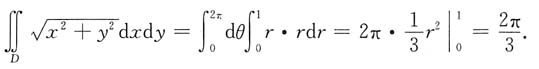
2. 设f(x,y)=e
-xsin(x+2y),则
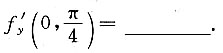
0
[解析] 由于f(0,y)=sin2y,则
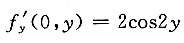
,所以
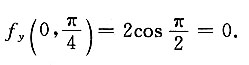
3. 设函数
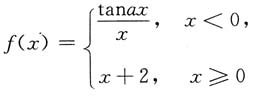
在x=0处连续,则a=______.
2
[解析]
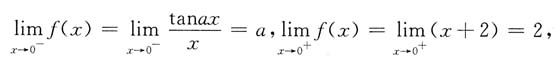
且f(0)=2,由连续的充要条件知a=2.
4. 曲线
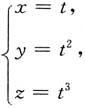
在点(-1,1,-1)处的切线方程为______.
[解析] 点(-1,1,-1)处对应的t=-1,
故切线的方向向量s={x'(t)|
t=-1,y'(t)|
t=-1,z'(t)|
t=-1}={1,-2,3}
故切线方程为
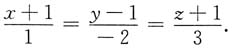
5. 曲线y=xe
-x的拐点是______.
(2,2e-2)
[解析] 因为y'=(1-x)e-x,y"=(x-2)e-x,令y"=0得x=2,
当x<2时,y"<0,当x>2时,y">0,
故拐点坐标为(2,2e-2).
6. 设y=sin(lnx
2),则y'=______.
[解析]
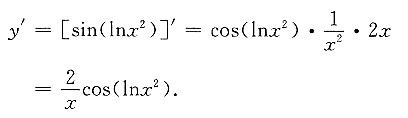
7.
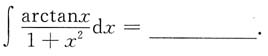
[解析]
8. 向量组α
1=(1,2,-1,1),α
2=(2,0,3,0),α
3=(-1,2,-4,1)的秩为______.
2
[解析]
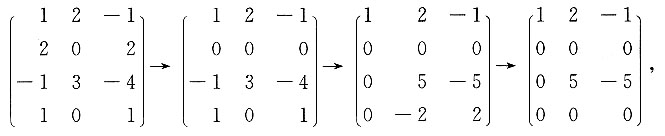
因此,α
1,α
2,α
3的秩为2.
10. 若z=x+y+f(x-y),且当y=0时z=x
2,则f(x)=______.
x2-x
[解析] 取y=0,得x2=x+f(x),所以f(x)=x2-x.
三、解答题1. 如果某产品Q(单位:吨)Q=10000-100P,生产该产品的成本函数为TC=6000+20Q,求:
(1)利润最大化时的产量;
(2)政府对生产者征税每吨10元时,利润最大化时的产量及利润.
(1)由已知条件得:P=100-0.01Q,利润函数为
π=TR-TC=PQ-TC=(100-0.01Q)Q-6000-20Q
=80Q-0.01Q
2-6000,
根据利润最大化一阶条件π'=0,得
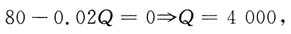
利润最大化时的产量为4000;
(2)政府对生产者征税后,新成本函数为TC=6000+30Q,利润函数为
π=TR-TC=PQ-TC=(100-0.01Q)Q-6000-30Q=70Q-0.01Q
2-6000,
根据利润最大化一阶条件π'=0,得
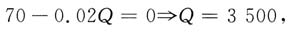
利润最大化时的利润为
π=TR-TC=PQ-TC
=65×3500-6000-30×3500=116500.
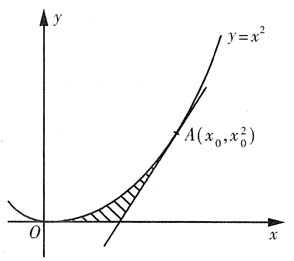
2. 过曲线y=x
2(x≥0)上某点A作切线,若切线、曲线、x轴围成的面积为
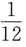
,求该图形绕x轴旋转一周所得旋转体的体积.
设A点坐标为
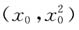
,由y'=2x得切线方程为
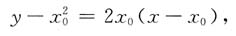
即
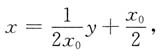
由
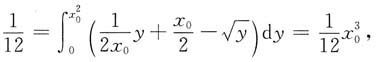
所以x
0=1,切点A(1,1).
切线方程为2x-y-1=0,切线与x轴交点为
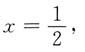
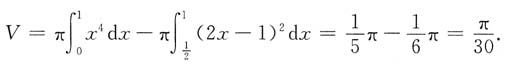
3. 设y=f(x)由xy+ey=e所确定,求y'(0).
x=0,y=1.两边对x求导,得
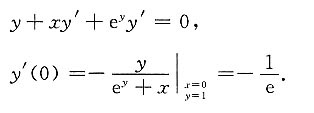
4. 用夹逼准则求极限