一、单项选择题2. 设f(x)的一个原函数为e
x,则
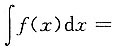
______
- A.xex+C
- B.ex+xex+C
- C.xex-ex+C
- D.ex+C
A B C D
D
[解析] 由题意知f(x)=(e
x)'=e
x,则
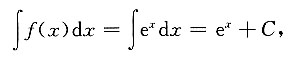
故选D.
3. 5人排成一行,甲、乙两人排在一起的概率P=______
A.
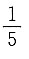
B.

C.
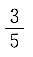
D.
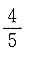
A B C D
B
[解析] 事件总数为
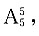
甲、乙两人排在一起的事件总数为
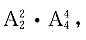
因此甲、乙两人排在一起的概率

.故应选B.
7. 曲线
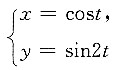
在
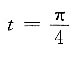
处的法线方程为______
A.
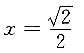
B.y=1
C.y=x+1
D.y=x-1
A B C D
A
[解析]
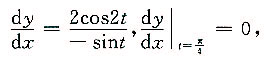
切线斜率k=0,故法线方程为
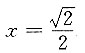
.故应选A.
9. 极限
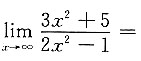
______
A.∞
B.0
C.
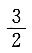
D.1
A B C D
C
[解析]
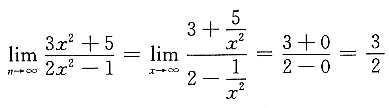
,故应选C.
二、填空题1. 设方程x=y
y确定y是x的函数,则dy=______.
[解析] 两边取自然对数lnx=ylny,
再两边求微分得
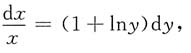
所以
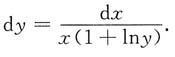
2. 设连续随机变量X的分布函数为
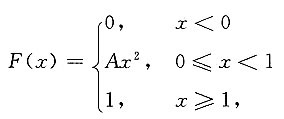
,则A=______.
1
[解析] 由F(x)的连续性,有
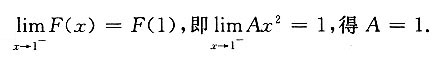
3.
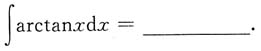
[解析]
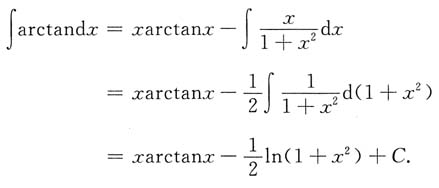
4. 以y=C
1e
-3x+C
2xe
-3x为通解的二阶常系数齐次线性微分方程为______.
y"+6y'+9y=0
[解析] 由y=C1e-3x+C2xe-3x为通解知,特征方程有二重特征根r=-3,特征方程为(r+3)2=0,即r2+6r+9=0,所以微分方程为y"+6y'+9y=0.
5. 曲线
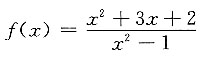
的垂直渐近线有______条.
1
[解析] 因为
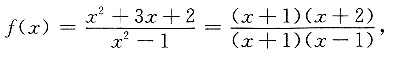
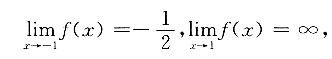
只有x=1一条垂直渐近线.
6.
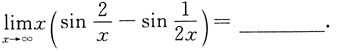
[解析]
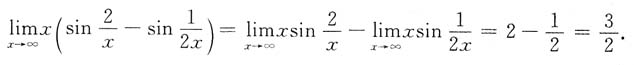
7. 函数
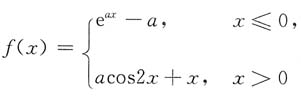
是连续函数,则a=______.
[解析]
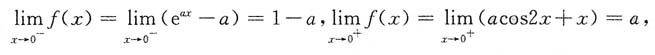
由f(x)的连续性,知1-a=a,即
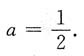
8. 曲线y=x+e
x在点(0,1)处的切线斜率k=______.
2
[解析] y'=1+ex,则x=0时,y'|x=0=2,即k=2.
9. 设
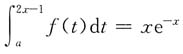
,则f(x)=______.
[解析] 对
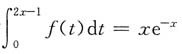
两边求导,得
2f(2x-1)=e
-x-xe
-x=(1-x)e
-x,
即
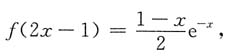
设t=2x-1则
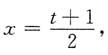
代入得
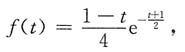
所以
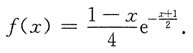
三、解答题1. 设z=f(x
2+y
2,y)+φ(xy),其中,f(u,v)和φ(x)都可微,求全微分dz.
令x2+y2=u,y=v,则z=f(u,v)+φ(xy),
dz=df(u,v)+dφ(xy)
=fudu+fvdv+φ(xy)d(xy)
=fu(2xdx+2ydy)+fvdy+φ(xy)·(xdy+ydx)
=[2xfu+yφ(xy)]dx+[2yfu+fv+xφ(xy)]dy.
2. 求曲线x=t,y=2t
2,z=t
2在点(1,2,1)处的切线与法平面方程.
点(1,2,1),对应t=1,
x'(t)=1,y'(t)=4t,z'(t)=2t,
对应的方向向量也即是法向量为l=n={1,4,2},
所求的切线方程为
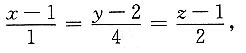
法平面为(x-1)+4(y-2)+2(z-1)=0.
即x+4y+2z-11=0.
3. 设z=f(e
xsiny,ln(x+y)),其中,f(u,v)为可微函数,求
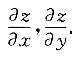
设u=e
xsiny,v=ln(x+y),则z=f(u,v),
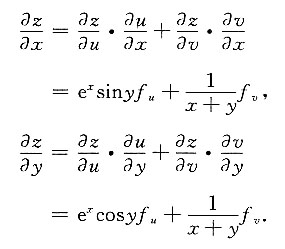
4. 求线性方程组
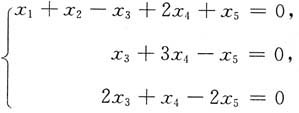
的通解.
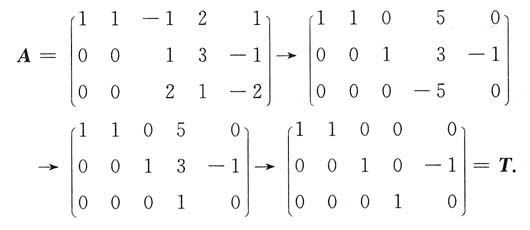
同解方程组为
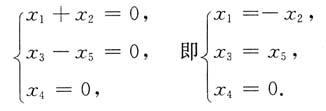
分别取x
2=1,x
5=0和x
2=0,x
5=1可得基础解系
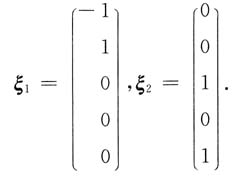
于是,线性方程组的通解为ξ=k
1ξ
1+k
2ξ
2,k
1和k
2为任意实数.
5. 将函数
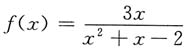
展开成x的幂级数,并写出其收敛区间.