一、单项选择题1. f(x)在点x=1处可导,且取得极小值,则
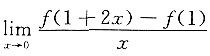
等于______
A.0
B.1
C.2
D.
A B C D
A
[解析]
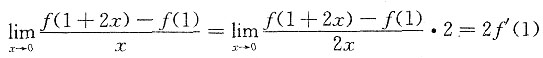
,因为f(x)在x=1处可导,且取得极小值,所以f'(1)=0,因此
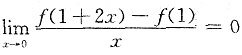
,故应选A.
6. 由参数方程
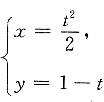
确定函数y(x)的二阶导数
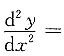
______
A.
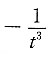
B.
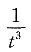
C.
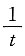
D.
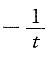
A B C D
B
[解析] 因为
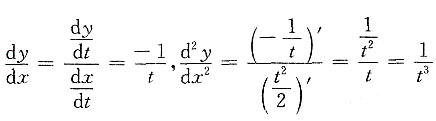
,故应选B.
7. 设f(1)=0,且极限
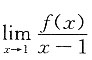
存在,则
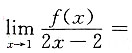
______
A.
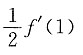
B.
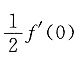
C.f'(1)
D.f'(0)
A B C D
A
[解析]
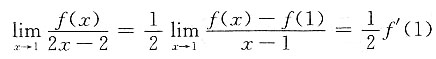
,故应选A.
10. 已知函数f(x)可导,且
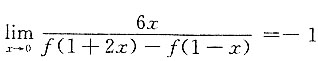
,则曲线y=f(x)在点(1,f(1))处的切线斜率为______
A.
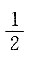
B.
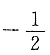
C.2
D.-2
A B C D
D
[解析] 因为
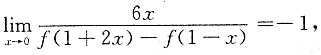
所以
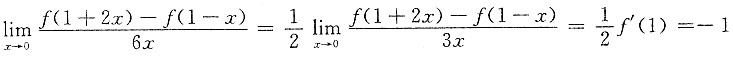
,即f'(1)=-2.故应选D.
二、填空题1. 曲线方程为3y
2=x
2(x+1),则在点(2,2)处的切线方程为______.
4x-3y-2=0
[解析] 两边对x求导得6y·y'=3x
2+2x,即
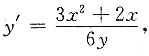
k=y'|
(2,2) 切线方程为
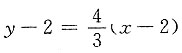
即4x-3y-2=0.
2. 方程(y")
3-xy'+cosy=x
2+1是______阶微分方程.
二
[解析] 由微分方程的基本概念可知(y")3-xy'+cosy=x2+1是二阶微分方程.
3. 由z
3-2xz+y=0确定隐函数x=x(y,z),则
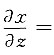
______.
[解析] 令F(x,y,z)=z
3-2xz+y,
则F
x=-2z,F
z=3z
2-2x,
所以
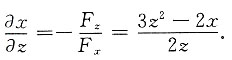
4. 已知函数y=x
x,则dy=______.
(1+lnx)xxdx
[解析] y=x
x=e
xlnx,则

所以dy=(1+lnx)x
xdx.
5. 设函数f(x)=e
tanx,则df(x)=______.
sec2xetanxdx
[解析] d(etanx)=etanx·(tanx)'dx=sec2xetanxdx.
6. 点M(3,2,-1)到平面x+y+z-1=0的距离为______.
[解析]
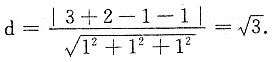
7. 设函数f(x)=4x+1,则f[f(x)-1]=______.
16x+1
[解析] f[f(x)-1]=f(4x+1-1)=f(4x)=4·4x+1=16x+1.
8. 设f(x+y,xy)=x
2+3xy+y
2+5,则f(x,y)=______.
x2+y+5
[解析] f(x+y,xy)=x2+3xy+y2+5=(x+y)2+xy+5,
所以f(x,y)=x2+y+5.
9. 若
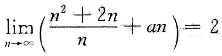
,则a=______.
-1
[解析] 因为
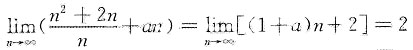
,所以a+1=0,即a=-1.
10. 函数y=x
3-27x+2在[0,1]上的最大值为______.
2
[解析] 因为f'(x)=3x2-27,当0<x<1时f'(x)<0所以f(x)在[0,1]上单调减少,最大值为f(0)=2.
三、计算题1. 求曲面e
z-z+xy=3在点(2,1,0)处的切平面及法线方程.
令F(x,y,z)=e
z-z+xy-3,则
n={F
x,F
y,F
z}={y,x,e
z-1},n|
(2,1,0)={1,2,0},
曲面在点(2,1,0)处的切平面方程为
1·(x-2)+2(y-1)+0·(z-0)=0,
即x+2y-4=0.
所求法线方程为

2. 求

3. 已知曲线y=ax
3+bx
2+cx在点(1,2)处有水平切线,且原点为该曲线的拐点,求曲线方程.
y'=3ax2+2bx+c,y"=6ax+2b,
因为点(1,2)在曲线上,所以a+b+c=2,①
又因为点(1,2)处有水平切线,所以y'|x=1=3a+2b+c=0,②
又原点为曲线的拐点,得y"|x=0=2b=0,③
联立①、②、③解得a=-1,b=0,c=3,
故曲线方程为y=-x3+3x.
4. 求微分方程2y"+y'-y=3e
x的通解.
对应齐次方程的特征方程为2r
2+r-1=0,
解得特征根为r
1=-1,
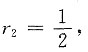
所以对应齐次方程的通解为
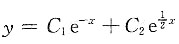
,(C
1,C
2为任意常数).
又因为λ=1不是特征根,可设特解为y
*=Ae
x,
代入原方程得2Ae
x+Ae
x-Ae
x=3e
x,解得
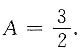
故所求方程的通解为
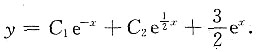
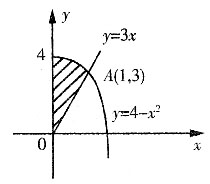
四、应用题1. 求抛物线y=4-x
2与直线y=3x及y轴所围成第一象限内平面图形的面积,并求该图形绕y轴旋转一周得到旋转体的体积.
平面图形如图所示,
由
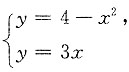
得第一象限内的交点为A(1,3),
所求面积为
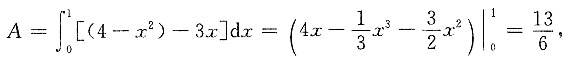
所求体积为
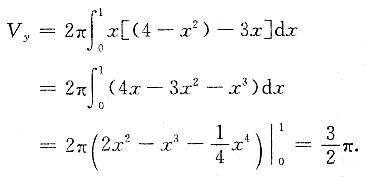
五、证明题1. 设函数f(x)在[0,1]上连续,并且对于[0,1]上的任意x所对应的函数值f(x)均有0≤f(x)≤1,证明:在[0,1]上至少有一点ξ,使得f(ξ)=ξ.
证:令G(x)=f(x)-x,
∵f(x)在[0,1]上连续,
∴G(x)在[0,1]上连续.
∵对
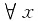
∈[0,1]均有0≤f(x)≤1,
∴0≤f(0)≤1,0≤f(1)≤1,
∴G(0)=f(0)-0=f(0)≥0,G(1)=f(1)-1≤0,
∴由零点定理知,至少存在一点ξ∈[0,1],使得G(ξ)=0,即f(ξ)-ξ=0,
∴在[0,1]上至少有一点ξ,使得f(ξ)=ξ.