一、单项选择题8. 设f(x)为连续函数,则
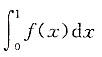
______
A.
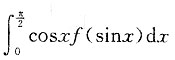
B.
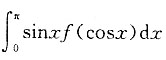
C.
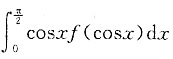
D.
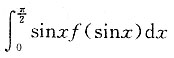
A B C D
A
[解析]
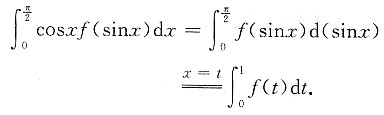
故应选A.
10. 由方程xy+lny=1确定的隐函数x=x(y)的微分dx______
A.
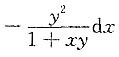
B.
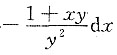
C.
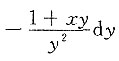
D.
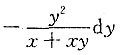
A B C D
C
[解析] 两边微分,得
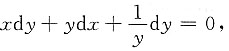
即(xy+1)dy+y
2dx=0,
所以
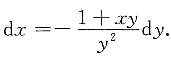
故应选C.
二、填空题1. 微分方程y"-4y=0的通解是______.
y=C1e-2x+C2e2x
[解析] 特征方程为r2-4=0,解得r1=-2,r2=2,所以通解为y=C1e-2x+C2e2x.
2. 设区域D为x
2+y
2≤9,则
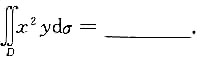
0
[解析] 根据二重积分的对称性知其值为0.
或
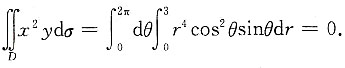
3. 函数y=sinx-x在区间[0,π]上的最大值是______.
0
[解析] y'=cosx-1≤0,故y在[0,π]上单调递减,故最大值为y(0)=0.
4.
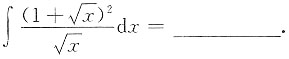
[解析]
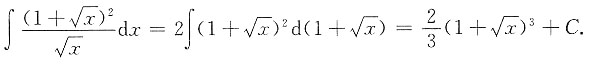
5. 设f(x)-x(x+1)(x+2)…(x+2015),则f'(0)=______.
2015!
[解析]
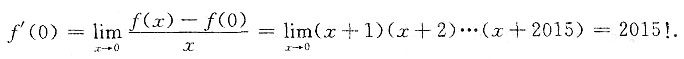
6.
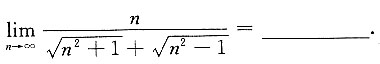
[解析]
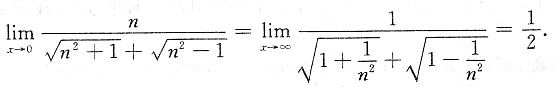
7. 参数方程
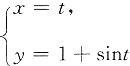
在t=π处切线方程为______.
x+y-1-π=0
[解析]
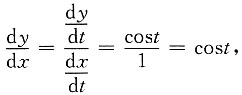
所以k=cost|
t=π=-1,当t=π时,x=π,y=1,所以t=π处的切线方程为y-1=-1(x-π),即x+y-1-π=0.
8. 以y=C
1e
-3x+C
2xe
-3x为通解的二阶常系数齐次线性微分方程为______.
y"+6y'+9y=0
[解析] 由y=C1e-3x+C2xe-3x为通解知,特征方程有二重特征根r=-3,特征方程为(r+3)2=0,即r2+pr+q=0,所以微分方程为y"+6y'+9y=0.
9. 以y=C
1+C
2x
2为通解的微分方程为______.
xy"-y'=0
[解析] y'=2C2x,y"=2C2,所以y'=xy",即xy"-y'=0.
10. 设区域D={(x,y)|x
2+y
2≤1},则
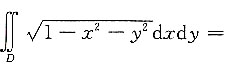
______.
[解析] D:0≤θ≤2π,0≤r≤1,
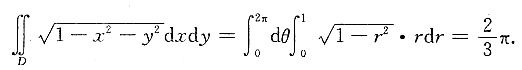
或根据二重积分的几何意义知
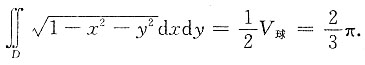
三、计算题1. 求微分方程y"-4y'+13y=0满足初始条件y|
x=0=0,y'|
x=0=3的特解.
特征方程为r
2-4r+13=0,
解得特征根为r
1,2=2±3i,
故方程的通解为y=e
2x(C
1cos3x+C
2sin3x),
且有y'=e
2x[(2C
1+3C
2)cos3x+(2C
2-3C
1)sin3x],
代入初始条件得
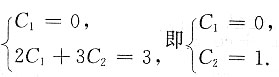
所以所求特解为y=e
2xsin3x.
2. 求
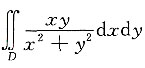
,其中D={(x,y)|y≥x,1≤x
2+y
2≤4}.
在极坐标系下
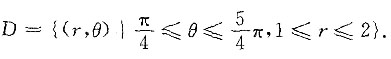
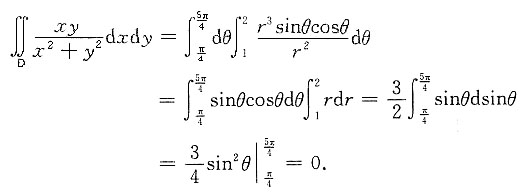
3. 求由隐函数x
2+3y
4+x+2y=1确定的导数

方程两边对x求导得2x+12y
3y'+1+2y'=0,整理得
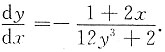
4. 求曲线
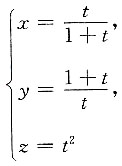
在对应于t=1的点处的切线及法平面方程.
曲线在对应于t=1的点为
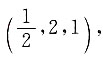
s={x'(1),y'(1),
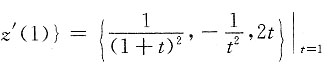

所以切线方程为
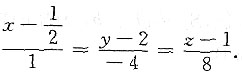
法平面方程为
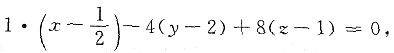
即2x-8y+16z-1=0.
四、应用题1. 某公司的甲、乙两厂生产同一种产品,月产量分别为x,y,(千件),甲厂的月生产成本是C
1=x
2-2x+5(千元),乙厂的生产成本是C
2=y
2+2y+3(千元),若要求该产品每月总产量为8千件,并使总成本最小,求甲、乙两厂的最优产量和相应的最小成本.
总成本为z=f(x,y)=x
2+y
2-2x+2y+8,
满足条件x+y=8,
作拉格朗日函数
L=x
2+y
2-2x+2y+8+λ(x+y-8),
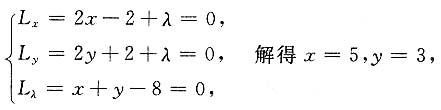
由于实际问题确有最小成本,且驻点(5,3)唯一,
所以当x=5千件,y=3千件时总成本最小,
最小成本为f(5,3)=38(千元).