银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
 B,则实a,b必满足______。
B,则实a,b必满足______。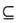 B,则有b-2≥a+1或b+2≤a-1,即b-a≥3或b-a≤-3,因此a,b必定满足|a-b|≥3。故本题选D。
B,则有b-2≥a+1或b+2≤a-1,即b-a≥3或b-a≤-3,因此a,b必定满足|a-b|≥3。故本题选D。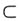 α,n∥α,则m∥n;
α,n∥α,则m∥n;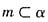 ,n∥α,则m和n可能平行也可能异面;命题②,假设α∩β=n,m为不在α,β内且平行于n的直线,则有m∥α,m∥β,所以由m∥α,m∥β,不能推出α∥β;命题③,若α∩β=n,m∥n,则m∥α或m∥β(m可能在α或β内);命题④,过m作两个不重合的平面,记这两个平面与α和β的交线分别为m',m"和n',n",则由m⊥α,m⊥β可以推出m'∥m",n'∥n",即找到了α内的一组平行于β的相交直线,所以α∥β。综上,四个命题中,真命题的个数是1。故本题选B。
,n∥α,则m和n可能平行也可能异面;命题②,假设α∩β=n,m为不在α,β内且平行于n的直线,则有m∥α,m∥β,所以由m∥α,m∥β,不能推出α∥β;命题③,若α∩β=n,m∥n,则m∥α或m∥β(m可能在α或β内);命题④,过m作两个不重合的平面,记这两个平面与α和β的交线分别为m',m"和n',n",则由m⊥α,m⊥β可以推出m'∥m",n'∥n",即找到了α内的一组平行于β的相交直线,所以α∥β。综上,四个命题中,真命题的个数是1。故本题选B。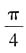
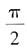
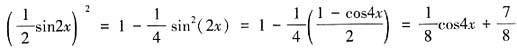 ,所以函数的最小正周期为
,所以函数的最小正周期为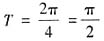 。故本题选B。
。故本题选B。 若z=2x-y的最大值为2,则实数m等于______。
若z=2x-y的最大值为2,则实数m等于______。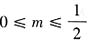 ,则可行域不是封闭区域,此时经过可行域内点的直线z=2x-y的截距-z可以无限小,从而z可以无限大,这与z的最大值为2矛盾;若m<-1或m≥2,则由图像可知,当直线z=2x-y经过原点(0,0)时,截距-z最小,此时z取得最大值0,这与z的最大值为2矛盾;若
,则可行域不是封闭区域,此时经过可行域内点的直线z=2x-y的截距-z可以无限小,从而z可以无限大,这与z的最大值为2矛盾;若m<-1或m≥2,则由图像可知,当直线z=2x-y经过原点(0,0)时,截距-z最小,此时z取得最大值0,这与z的最大值为2矛盾;若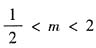 ,则当直线z=2x-y经过点
,则当直线z=2x-y经过点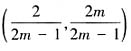 时,截距-z最小,此时z取得最大值
时,截距-z最小,此时z取得最大值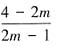 ,令
,令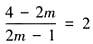 ,解得m=1,满足条件。故本题选C。
,解得m=1,满足条件。故本题选C。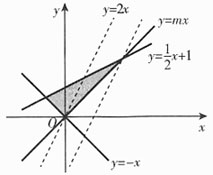
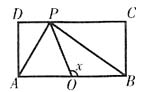
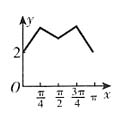
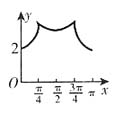
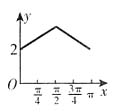
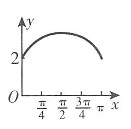
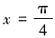 时,BP=1,
时,BP=1,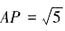 ,所以
,所以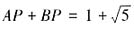 ;当
;当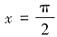 时,
时,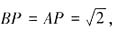 所以
所以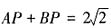 。因为
。因为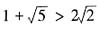 ,所以排除C项和D项。当
,所以排除C项和D项。当 不是一次函数,所以A项错误。故本题选B。
不是一次函数,所以A项错误。故本题选B。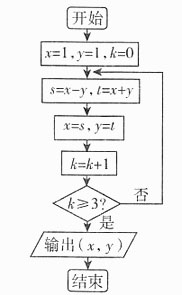
| x | 1 | 0 | -2 | -4 | ||||||||||||||||||
| y | 1 | 2 | 2 | 0 | ||||||||||||||||||
| k | 0 | 1 | 2 | 3 | ||||||||||||||||||
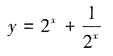
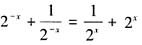 ,所以函数
,所以函数 是偶函数;D项,因为(-x)+sin2(-x)=-x-sin2x=-(x+sin2x),所以函数y=x+sin2x是奇函数。故本题选A。
是偶函数;D项,因为(-x)+sin2(-x)=-x-sin2x=-(x+sin2x),所以函数y=x+sin2x是奇函数。故本题选A。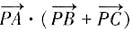 的最小值是______。
的最小值是______。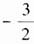
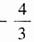
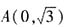 ,B(-1,0),C(1,0)。设点P的坐标为(x,y),则
,B(-1,0),C(1,0)。设点P的坐标为(x,y),则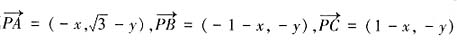 ,于是
,于是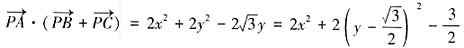 。显然当x=0,
。显然当x=0,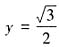 时,
时,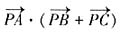 取得最小值
取得最小值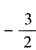 。故本题选B。
。故本题选B。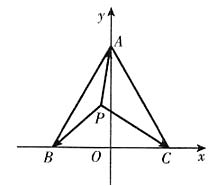
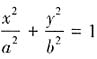 (a>b>0)的左、右焦点分别为F1,F2,线段F1F2被点
(a>b>0)的左、右焦点分别为F1,F2,线段F1F2被点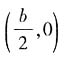 分成5:3的两段,则此椭圆的离心率为______。
分成5:3的两段,则此椭圆的离心率为______。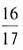
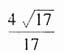
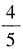
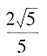
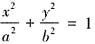 的焦距为2c,则F1,F2两点的坐标分别为(-c,0)和(-c,0)。因为F1F2被点
的焦距为2c,则F1,F2两点的坐标分别为(-c,0)和(-c,0)。因为F1F2被点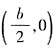 分成5:3的两段,所以有
分成5:3的两段,所以有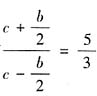 ,整理得c=2b,于是椭圆的离心率
,整理得c=2b,于是椭圆的离心率 。故本题选D。
。故本题选D。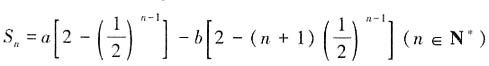 ,其中a,b是非零常数,则存在数列{xn},{yn}使得______。
,其中a,b是非零常数,则存在数列{xn},{yn}使得______。 ,所以当n≥2时,an=Sn-
,所以当n≥2时,an=Sn-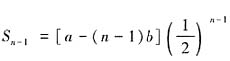 ,又a1=S1=a,满足
,又a1=S1=a,满足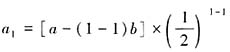 ,所以数列{an}的通项公式为
,所以数列{an}的通项公式为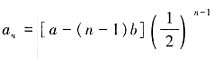 。观察数列{an}的通项公式,a-(n-1)b可以构成首项为a,公差为-b的等差数列;
。观察数列{an}的通项公式,a-(n-1)b可以构成首项为a,公差为-b的等差数列;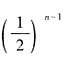 可以构成首项为1,公比为
可以构成首项为1,公比为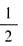 的等比数列。因此,取xn=a-(n-1)b,
的等比数列。因此,取xn=a-(n-1)b,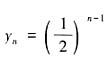 ,则an=xnyn其中{xn}为等差数列,{yn}为等比数列。故本题选C。
,则an=xnyn其中{xn}为等差数列,{yn}为等比数列。故本题选C。
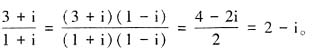
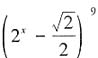 展开式的第7项为
展开式的第7项为 ,则实数x的值是______。
,则实数x的值是______。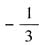
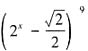 展开式的通项为
展开式的通项为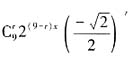 ,因为展开式的第7项为
,因为展开式的第7项为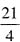 ,所以
,所以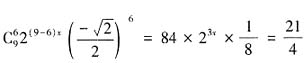 ,整理得
,整理得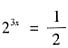 ,于是3x=-1,
,于是3x=-1,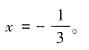
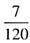

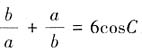 ,则
,则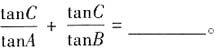
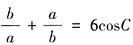 ,则由正弦定理可得,
,则由正弦定理可得,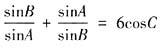 ,于是
,于是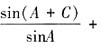
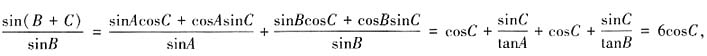 ,等式两边同除cosC得,
,等式两边同除cosC得,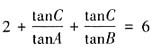 ,所以
,所以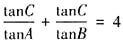 。
。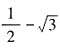
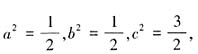 所以
所以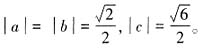 注意到,a与b的绝对值相等,且ab+bc+ca=ab+c(a+b),所以下面对a与b是否异号进行分类讨论。当a与b异号时,
注意到,a与b的绝对值相等,且ab+bc+ca=ab+c(a+b),所以下面对a与b是否异号进行分类讨论。当a与b异号时,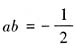 ,a+b=0,此时
,a+b=0,此时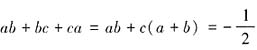 ;当a与b同号时,
;当a与b同号时, ,此时只需令c与a,b异号即可得到(a与b同号条件下)ab+bc+ca的最小值,最小值为
,此时只需令c与a,b异号即可得到(a与b同号条件下)ab+bc+ca的最小值,最小值为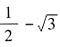 。因为
。因为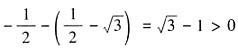 ,所以
,所以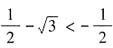 ,于是ab+bc+ca的最小值为
,于是ab+bc+ca的最小值为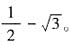 。
。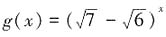 的图像关于直线x-y=0对称,则f(4-x2)的单调递增区间是______。
的图像关于直线x-y=0对称,则f(4-x2)的单调递增区间是______。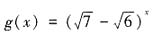 的图像关于直线x-y=0对称,所以函数f(x)与g(x)互为反函数,
的图像关于直线x-y=0对称,所以函数f(x)与g(x)互为反函数,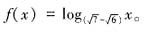 因为
因为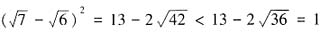 ,所以
,所以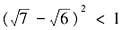 ,于是函数
,于是函数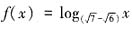 在(0,+∞)上单调递减,从而函数f(4-x2)的单调递增区间应为函数y=4-x2(y>0)的单调递减区间,即{x|x≥0,且4-x2>0}=[0,2)。
在(0,+∞)上单调递减,从而函数f(4-x2)的单调递增区间应为函数y=4-x2(y>0)的单调递减区间,即{x|x≥0,且4-x2>0}=[0,2)。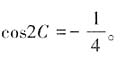
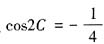 ,所以由半角公式可得,
,所以由半角公式可得,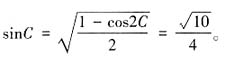
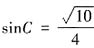 ,所以当a=2,2sinA=sinC时,由正弦定理可得,
,所以当a=2,2sinA=sinC时,由正弦定理可得,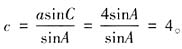 因为a=2<c=4,所以角A一定小于角c,于是角A一定是锐角,从而
因为a=2<c=4,所以角A一定小于角c,于是角A一定是锐角,从而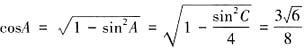 。考虑余弦定理,b2+c2-2bccosA=a2,将a=2,c=4,
。考虑余弦定理,b2+c2-2bccosA=a2,将a=2,c=4,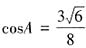 代入整理得,
代入整理得,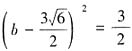 ,解得
,解得 。
。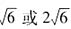 ,c的值为4。
,c的值为4。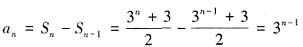 ;又
;又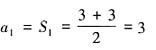 ,所以数列{an}的通项公式为
,所以数列{an}的通项公式为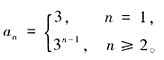
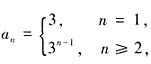 所以若数列{bn}满足anbn=log3an则有
所以若数列{bn}满足anbn=log3an则有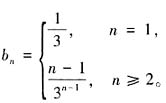 因此,当n≥2时,
因此,当n≥2时,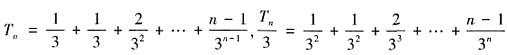 ,两式相减得,
,两式相减得,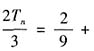
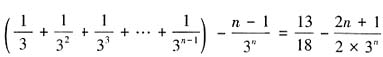 ,于是
,于是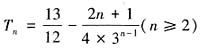 ,又
,又 ,满足
,满足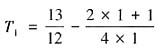 ,所以
,所以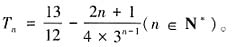
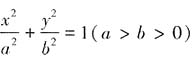 的离心率为
的离心率为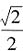 ,且右焦点F到左准线l的距离为3。
,且右焦点F到左准线l的距离为3。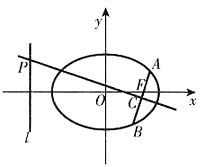
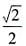 ,右焦点到左准线的距离为3,所以有
,右焦点到左准线的距离为3,所以有 ,两式联立解得,c=1,
,两式联立解得,c=1, ,于是
,于是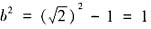 ,从而椭圆的标准方程为
,从而椭圆的标准方程为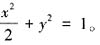
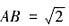 ,PC=3,不满足PC=2AB。
,PC=3,不满足PC=2AB。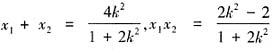 ,从而
,从而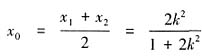 。根据弦长公式
。根据弦长公式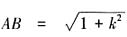
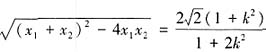 ,同时因为PC是AB的垂直平分线,且P在直线l上,所以直线PC的斜率为
,同时因为PC是AB的垂直平分线,且P在直线l上,所以直线PC的斜率为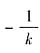 ,P点的横坐标为-2,于是
,P点的横坐标为-2,于是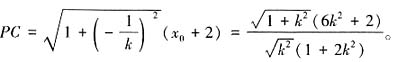 。因为PC=2AB,所以
。因为PC=2AB,所以 ,解得k=±1。故满足题意的直线AB的方程为y=±(x-1)。
,解得k=±1。故满足题意的直线AB的方程为y=±(x-1)。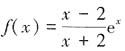 的单调性,并证明当x>0时,(x-2)ex+x+2>0;
的单调性,并证明当x>0时,(x-2)ex+x+2>0;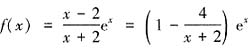 ,则
,则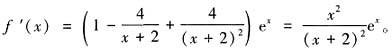 显然,
显然, 在R上恒成立,所以函数f(x)是增函数,又f(0)=-1,所以当x>0时,有f(x)=
在R上恒成立,所以函数f(x)是增函数,又f(0)=-1,所以当x>0时,有f(x)= ,不等式两边同乘x+2移项得,(x-2)ex+x+2>0,不等式得证。
,不等式两边同乘x+2移项得,(x-2)ex+x+2>0,不等式得证。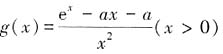 有最小值,设g(x)的最小值为h(a),求函数h(a)的值域。
有最小值,设g(x)的最小值为h(a),求函数h(a)的值域。 ,则
,则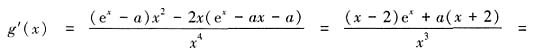
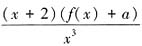 。由(1)知函数f(x)是增函数,且f(0)=-1f(2)=0,所以当a∈[0,1)时,在区间(0,2]内必定存在唯一一点xa使得
。由(1)知函数f(x)是增函数,且f(0)=-1f(2)=0,所以当a∈[0,1)时,在区间(0,2]内必定存在唯一一点xa使得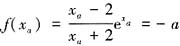 (同时可知,f(x)=-a是(0,2]到[0,1)的一一映射),从而当0<x<xa时,有g'(x)<0;当x>xa时,有g'(x)>0。因此,当函数a∈[0,1)时,g(x)在(0,+∞)上先减后增,在x=xa处取得最小值g(xa),这里xa满足f(xa)=-a。下面分析关于a的函数
(同时可知,f(x)=-a是(0,2]到[0,1)的一一映射),从而当0<x<xa时,有g'(x)<0;当x>xa时,有g'(x)>0。因此,当函数a∈[0,1)时,g(x)在(0,+∞)上先减后增,在x=xa处取得最小值g(xa),这里xa满足f(xa)=-a。下面分析关于a的函数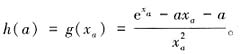
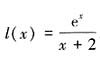 代入 h(a)得,
代入 h(a)得,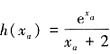 。令
。令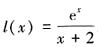 ,因为f(x)=-a是(0,2]到[0,1)的一一映射,所以h(a)的值域等于l(x)在区间(0,2]上的值域。对函数l(x)求导得,
,因为f(x)=-a是(0,2]到[0,1)的一一映射,所以h(a)的值域等于l(x)在区间(0,2]上的值域。对函数l(x)求导得,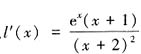 。显然,
。显然,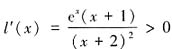 在(0,2]上恒成立,所以l(x)在(0,2]上单调递增,于是l(x)在(0,2]上的值域,也即h(a)的值域为
在(0,2]上恒成立,所以l(x)在(0,2]上单调递增,于是l(x)在(0,2]上的值域,也即h(a)的值域为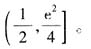


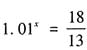 ,同理,如果计算哪一年人口总数达到20亿,30亿,则可列出式子
,同理,如果计算哪一年人口总数达到20亿,30亿,则可列出式子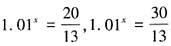 。让学生观察这几个式子,看看能发现什么。
。让学生观察这几个式子,看看能发现什么。 用对数的方式表达出来。教师巡视学生。
用对数的方式表达出来。教师巡视学生。

