一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设随机变量X~N(0,1),Y的分布为
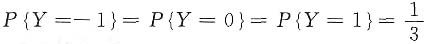
,且X,Y相互独立.记F
Z(z)为Z=XY的分布函数,则F
Z(z)的间断点个数为______
A B C D
B
[解析] 记y
1=-1,y
2=0,y
3=1,由事件分解:
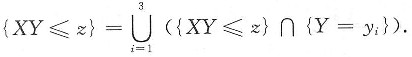
由全概率公式,得
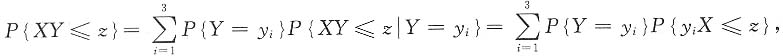
所以有
F
Z(z)=P(XY≤z)
=P(Y=-1)P[X·(-1)≤z]+P(Y=0)P(X·0≤z)+
P(Y=1)P(X·1≤z)
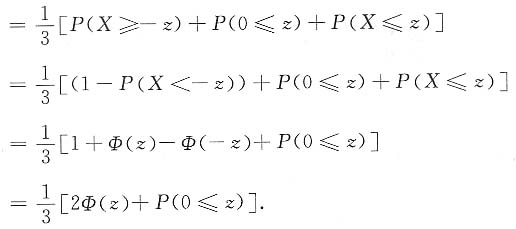
因为Φ(z)无间断点,因此只需考虑概率P(0≤z).
由于当z<0时,有P(0≤z)=0;当z>0时,有P(0<z)=1.
从而z=0是F
Z(z)的唯一间断点.
3. 设A,B为n阶矩阵,则下列结论正确的是______.
- A.若A2~B2,则A~B
- B.矩阵A的秩与A的非零特征值的个数相等
- C.若A,B的特征值相同,则A~B
- D.若A~B,且A可相似对角化,则B可相似对角化
A B C D
D
[解析] 由A~B得A,B的特征值相同,设为λ
1,λ
2,…,λ
n,
且存在可逆矩阵P
1,使得
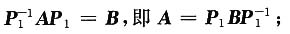
因为A可相似对角化,所以存在可逆矩阵P
2,使得
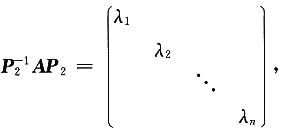
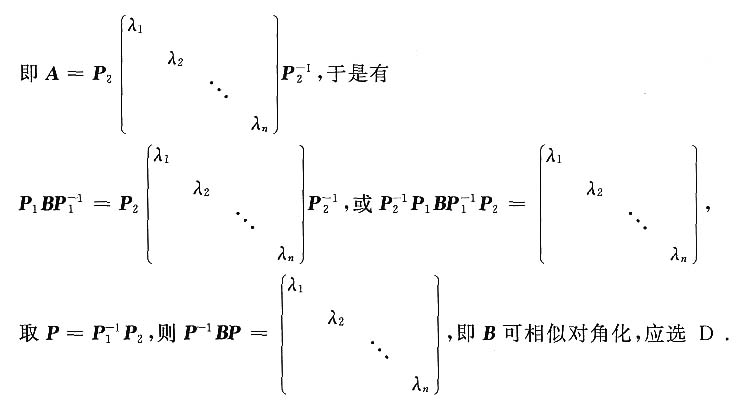
4. 设矩阵
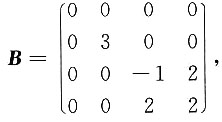
矩阵A~B,则r(A-E)+r(A-3E)=______
A B C D
A
[解析] 由矩阵B的特征多项式
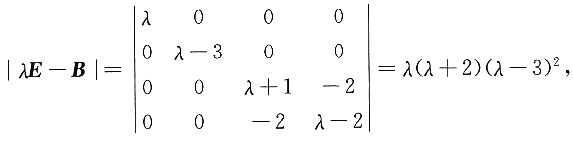
可得B的特征值为λ
1=0,λ
2=-2,λ
3=λ
4=3.因为A~B,所以矩阵A与矩阵B有相同的特征值.又因为B是实对称矩阵,故B可相似于对角矩阵.从而,矩阵A也可相似于对角矩阵.所以,矩阵A的2重特征值λ
3=λ
4=3,必有2个线性无关的特征向量.由此可知,r(3E-A)=n-2=4-2=2,即r(A-3E)=2.又因为λ=1不是矩阵A的特征值,从而|E-A|≠0.所以,r(E-A)=4,即r(A-E)=4.因此,r(A-E)+r(A-3E)=4+2=6.选A.
5. 设以a
n>0(n=1,2,…),下述命题正确的是______
A.设存在N>0,当n>N时,
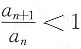
,则
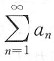
必收敛.
B.设
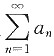
收敛,则必存在N>0,当n>N时,
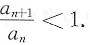
C.设存在N>0,当n>N时,
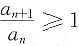
,则
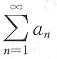
必发散.
D.设
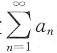
发散,则必存在N>0,当n>N时,
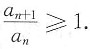
A B C D
C
[解析] 在C的条件下,必有
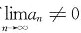
,从而推知级数发散.A的反例:
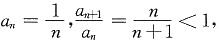
但
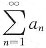
发散;B的反例:
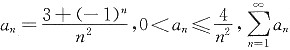
收敛.但当n为奇数时,
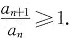
D的反例见A的反例.
6. 矩阵
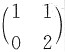
与______相似.
A.
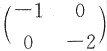
B.
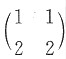
C.
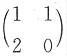
D.
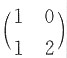
A B C D
D
[考点] 矩阵相似的判别.
[解析] 利用矩阵相似的必要条件排除A、B、C项;或者直接判别题目中矩阵与D项的矩阵都与同一个对角阵相似.
解:令矩阵
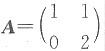
,则A的特征值为1和2.
而A选项中矩阵的特征值为-1和-2,故矩阵A不与A选项的矩阵相似.
又因为
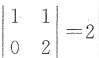
,而B选项中
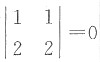
,C选项中
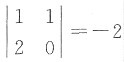
,故矩阵A不与B、C选项的矩阵相似.
所以,矩阵A与D选项的矩阵相似.
事实上,
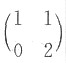
和
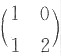
均与对角阵
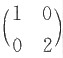
相似.再由相似的传递性,
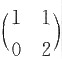
和
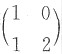
相似.
故应选D.
7. 设函数f(u,v)连续,
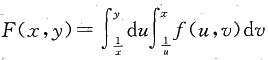
,则
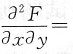
A.f(x,y).
B.f(y,x).
C.
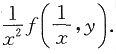
D.
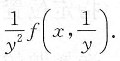
A B C D
B
[解析] 交换积分次序,则有
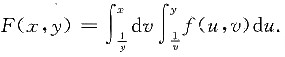
记
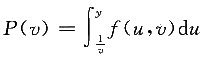
,则
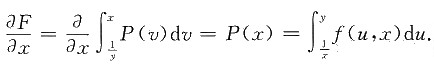
两边再对y求导,
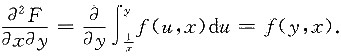
二、填空题1. 设f(x)连续,对于任意x>0,f(x)>0,且有
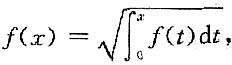
贝0当x≥0时,f(x)=______.
[解析] 当x=0,

又
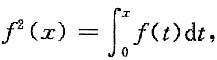
两边求导,得2f(x)f'(x)=f(x);
当x>0,f(x)>0,
∴
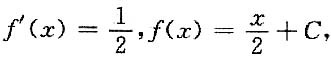
又f(0)=0,∴C=0.
2. 曲线
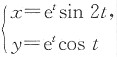
在点(0,1)处的法线方程为______.
2x+y-1=0
[考点] 参数方程的导数及导数的几何意义.
[解析] 利用参数方程求导可求得切线斜率,从而得到法线斜率.
解:
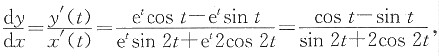
当x=0时,t=0,
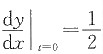
.
所以法线斜率k=-2,则曲线在点(0,1)处的法线方程为
y-1=-2x,即2x+y-1=0.
故应填2x+y-1=0.
3. 设f(x)连续,且f(0)=0,f'(0)=2,则
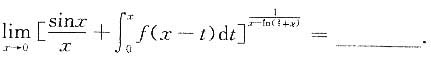
[解析]
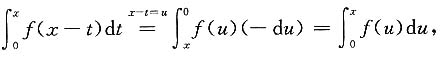
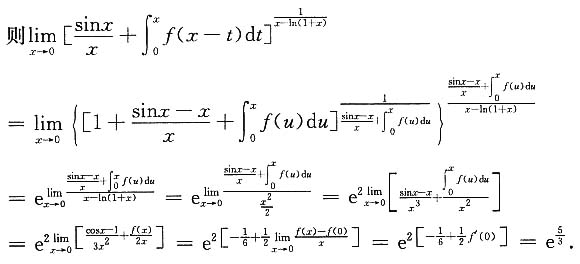
4. 直线
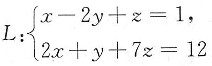
在yOz平面上的投影直线l绕Oz轴旋转一周生成的旋转曲面的方程为______.
x2+y2-z2+4z-4=0
[解析] 直线

在yOz平面上的投影直线l的方程为y+z=2,即y=2-z,它绕Oz轴旋转一周生成的旋转曲面方程为
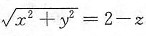
,即x
2+y
2=4-4z+z
2,即如答案所示.
5. 函数f(x,y)=3+9x-6y+4x
2-5y
2+2xy+x
3+2xy
2-y
3在点(1,-1)展开至n=2的泰勒公式为f(x,y)=______+R
2,其中余项R
2=______.
[解析] x
0=1,y
0=-1,则
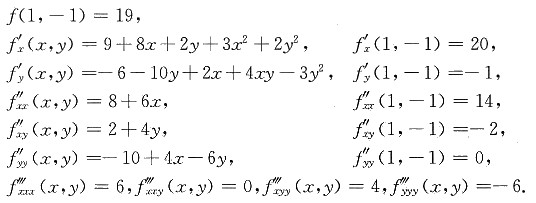
所以f(x,y)在点(1,-1)处的2阶泰勒公式为
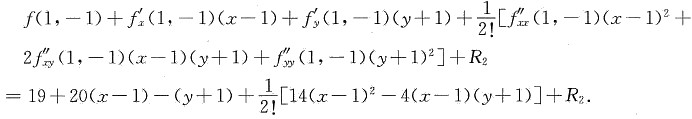
2阶泰勒公式的余项
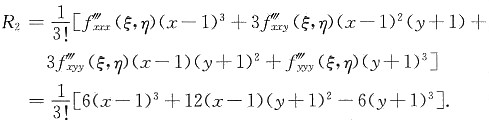
6.

三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.1. 设f(x),g(x)二阶可导,当x>0时,f"(x)>g"(x)且f(0)=g(0),f'(0)=g'(0),证明:当x>0时,f(x)>g(x).
证明:令
F(x)=f(x)-g(x),
F'(x)=f'(x)-g'(x),
F"(x)=f"(x)-g"(x).
因为当x>0时,f"(x)>g"(x),所以当x>0时,F"(x)>0,即F'(x)单调递增.
又f'(0)=g'(0),即F'(0)=0.所以F'(x)>F'(0)=0,因之F(x)单调递增.
又因为f(0)=g(0),即F(0)=0,故F(x)>F(0)=0.
即f(x)-g(x)>0,亦即f(x)>g(x).
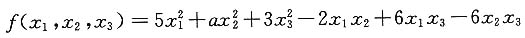 的矩阵合同于
的矩阵合同于
2. 求常数a;
解:
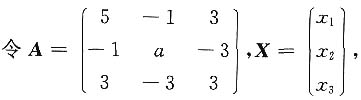
则f(x
1,x
2,x
3)=X
TAX.
因为A与
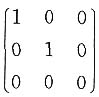
合同,所以r(A)=2<3,故|A|=0.
由|A|=
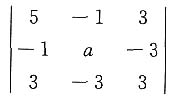
=3(2a-10)=0,得a=5,
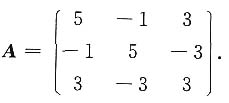
3. 用正交变换法化二次型f(x
1,x
2,x
3)为标准形.
解:由|λE-A|=
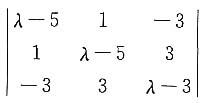
=λ(λ-4)(λ-9)=0,得λ
1=0,λ
2=4,λ
3=9.
由(0E-A)X=0得
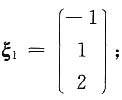
由(4E-A)X=0得
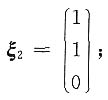
由(9E-A)X=0得
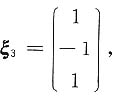
单位化得
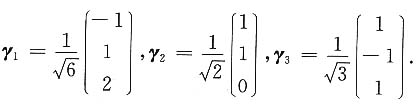
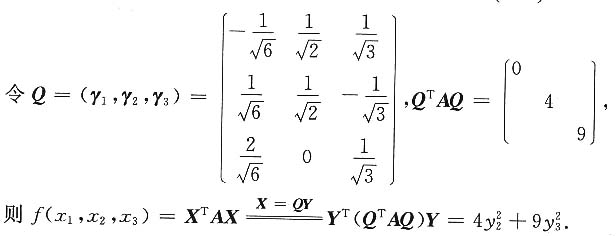
4. 设由
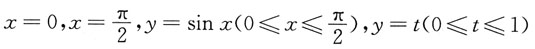
所围区域的面积为S(t),求S(t)的最大值与最小值.
解:如图所示,
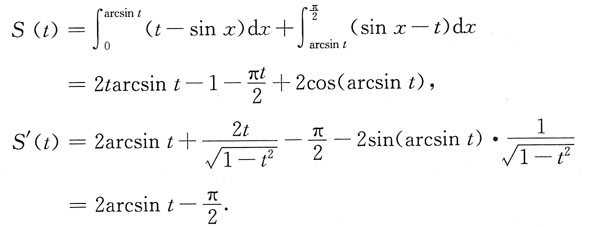
由S'(t)=0解出唯一驻点
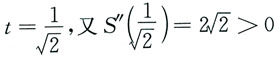
,因此
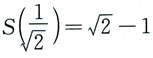
为极小值.又
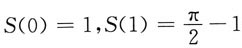
,所以S(t)最大值为1,最小值为
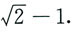
5. 设A,B均为n阶方阵,ABA=B
-1,E为n阶单位阵,证明:
r(E-AB)+r(E+AB)=n.
证明:因为ABA=B
-1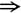
ABAB=E
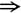
(E-AB)(E+AB)=O,
所以r(E-AB)+r(E+AB)≤n. ①
又(E-AB)+(E+AB)=2E,
所以r(E-AB)+r(E+AB)≥r(2E)=n, ②
由①,②,得r(E-AB)+r(E+AB)=n.
6. 已知f(x)在x=a处可导,且f(x)>0,n为自然数.
求
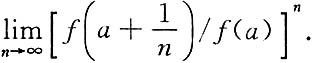
解:
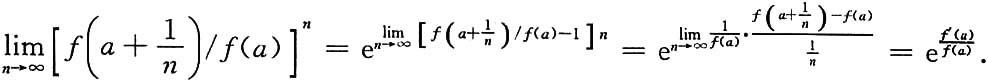
7. 证明:向量组α
1,α
2,α
3线性无关.
证明:由Aα1=α1得(A-E)α1=0,
由Aα2=α1+α2得(A-E)α2=α1,
由Aα3=α2+α3得(A-E)α3=α2.
令k1α1+k2α2+k3α3=0 1)
两边左乘以(A-E)得
k2α1+k3α2=0, 2)
两边再左乘(A-E)得k3α1=0,
由α1≠0得k3=0,代入2)得k2α1=0,则k2=0,
再代入1)得k1α1=0,从而k1=0,于是α1,α2,α3线性无关.
8. 证明:A不可相似对角化.
证明:令P=(α
1,α
2,α
3),
由(Aα
1,Aα
2,Aα
1)=(α
1,α
1+α
2,α
2+α
3)得
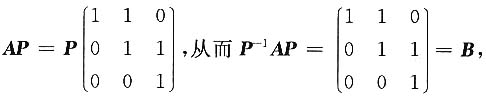
由|λE-A|=|λE-B|=(λ-1)
3=0得A的特征值为λ
1=λ
2=λ
3=1,
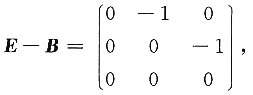
因为r(E-B)=2,所以B只有一个线性无关的特征向量,即B不可相似对角化,
而A~B,故A不可相似对角化.
9. 计算三对角行列式D
n之值.

解:按第一列展开得
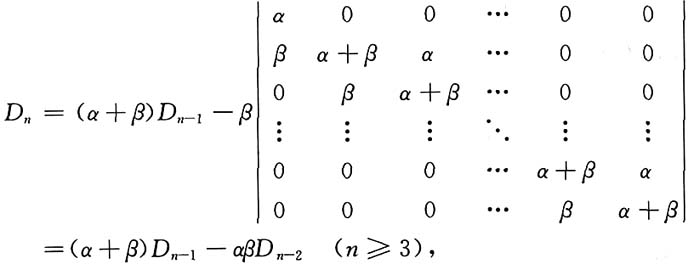
即有递推关系式D
n=(α+β)D
n-1-αβD
n-2.
为了得到D
n的一般表达式,采用上述方法1°求解
因为(假设α≠β),
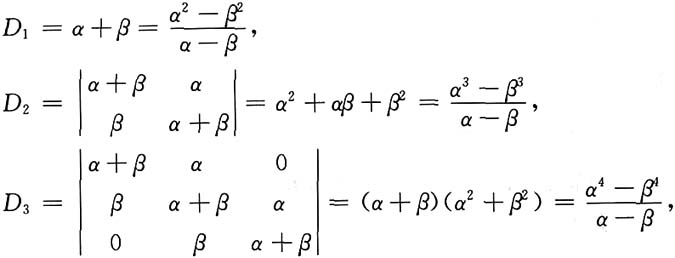
不妨设
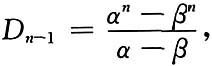
则有
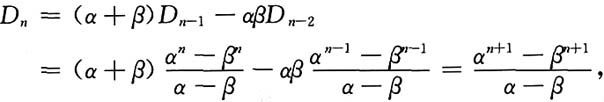
根据数学归纳法即知
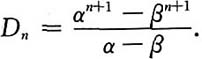
若α=β,可直接计算得D
n=(n+1)α
n.
10. 这个球是红球的概率;
解:A=“取得一个红球”,
B
i=“第i盒中取出一个红球”,(i=1,2).
于是,
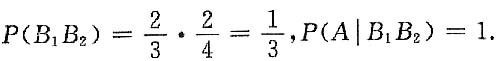
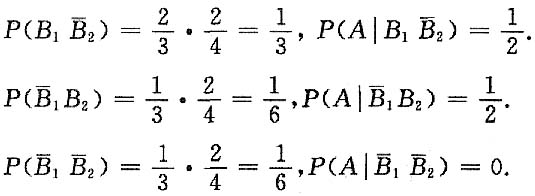
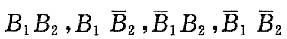
构成一个完备事件群.
所以,
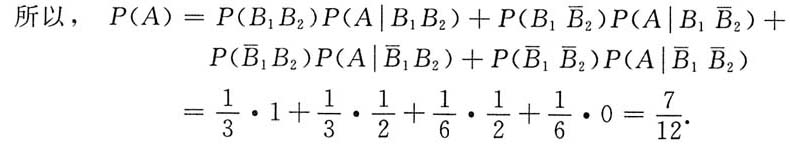
11. 重复上述过程10次,记X表示出现取出的球为红球的次数,求EX
2.
12. 将函数
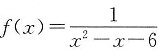
展开成(x-1)的幂级数.
解:
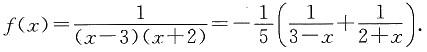
因为
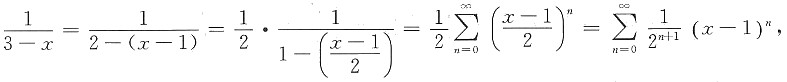
又
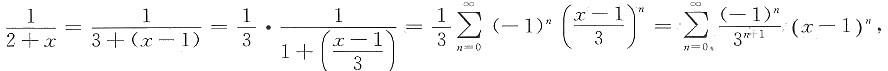
所以
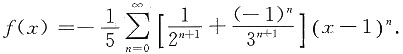
由
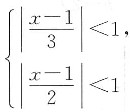
可知-1<x<3,故展开式成立的范围是(-1,3).
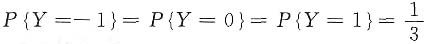 ,且X,Y相互独立.记FZ(z)为Z=XY的分布函数,则FZ(z)的间断点个数为______
,且X,Y相互独立.记FZ(z)为Z=XY的分布函数,则FZ(z)的间断点个数为______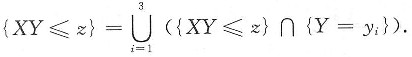
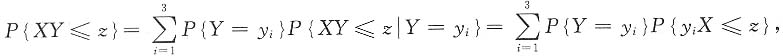
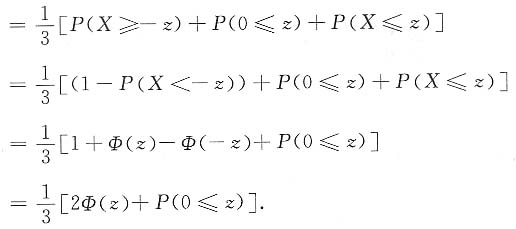
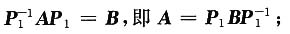
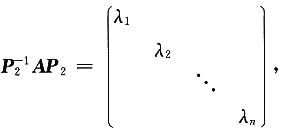

 矩阵A~B,则r(A-E)+r(A-3E)=______
矩阵A~B,则r(A-E)+r(A-3E)=______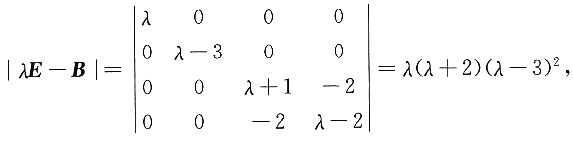
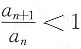 ,则
,则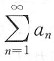 必收敛.
必收敛.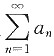 收敛,则必存在N>0,当n>N时,
收敛,则必存在N>0,当n>N时,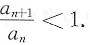
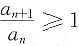 ,则
,则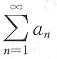 必发散.
必发散.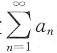 发散,则必存在N>0,当n>N时,
发散,则必存在N>0,当n>N时,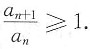
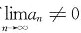 ,从而推知级数发散.A的反例:
,从而推知级数发散.A的反例: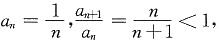 但
但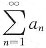 发散;B的反例:
发散;B的反例: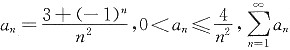 收敛.但当n为奇数时,
收敛.但当n为奇数时,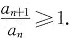 D的反例见A的反例.
D的反例见A的反例.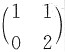 与______相似.
与______相似.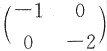
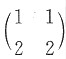
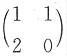
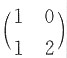
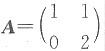 ,则A的特征值为1和2.
,则A的特征值为1和2.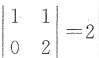 ,而B选项中
,而B选项中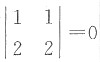 ,C选项中
,C选项中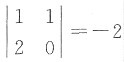 ,故矩阵A不与B、C选项的矩阵相似.
,故矩阵A不与B、C选项的矩阵相似.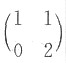 和
和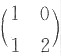 均与对角阵
均与对角阵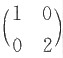 相似.再由相似的传递性,
相似.再由相似的传递性,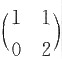 和
和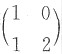 相似.
相似.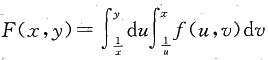 ,则
,则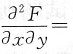
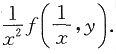
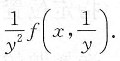
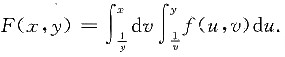
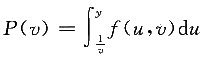 ,则
,则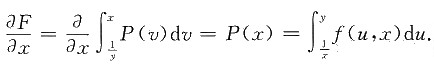
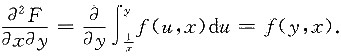
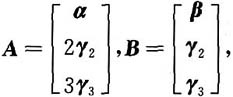 其中α,β,γ2,γ3均为三维行向量,且已知行列式|A|=18,|B|=2,则行列式|A-B|等于
其中α,β,γ2,γ3均为三维行向量,且已知行列式|A|=18,|B|=2,则行列式|A-B|等于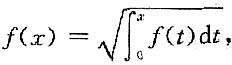 贝0当x≥0时,f(x)=______.
贝0当x≥0时,f(x)=______.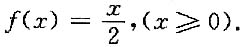

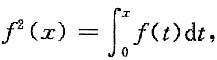 两边求导,得2f(x)f'(x)=f(x);
两边求导,得2f(x)f'(x)=f(x);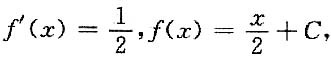 又f(0)=0,∴C=0.
又f(0)=0,∴C=0.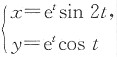 在点(0,1)处的法线方程为______.
在点(0,1)处的法线方程为______.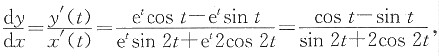
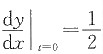 .
.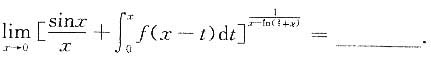
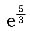
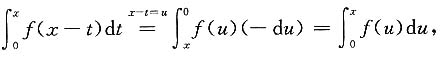
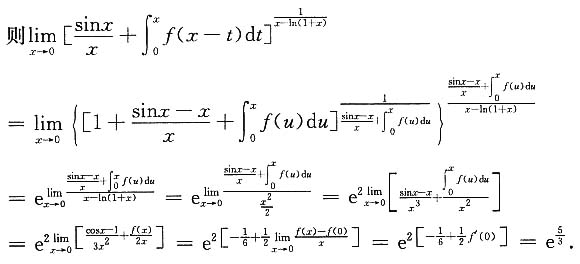
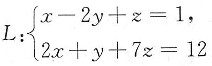 在yOz平面上的投影直线l绕Oz轴旋转一周生成的旋转曲面的方程为______.
在yOz平面上的投影直线l绕Oz轴旋转一周生成的旋转曲面的方程为______. 在yOz平面上的投影直线l的方程为y+z=2,即y=2-z,它绕Oz轴旋转一周生成的旋转曲面方程为
在yOz平面上的投影直线l的方程为y+z=2,即y=2-z,它绕Oz轴旋转一周生成的旋转曲面方程为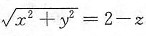 ,即x2+y2=4-4z+z2,即如答案所示.
,即x2+y2=4-4z+z2,即如答案所示.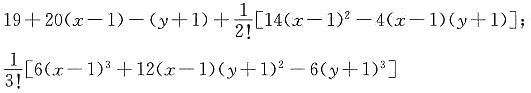
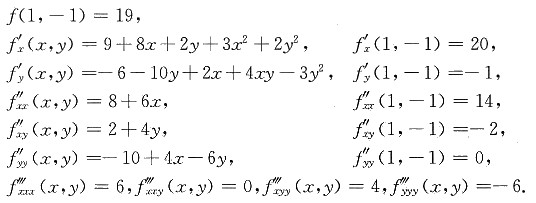
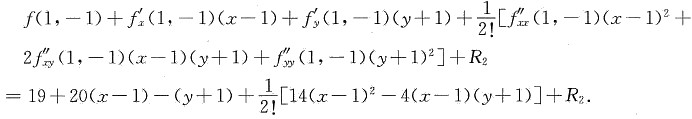
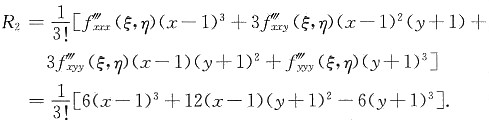

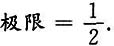
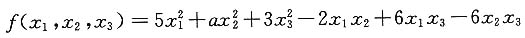 的矩阵合同于
的矩阵合同于
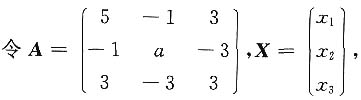 则f(x1,x2,x3)=XTAX.
则f(x1,x2,x3)=XTAX. 合同,所以r(A)=2<3,故|A|=0.
合同,所以r(A)=2<3,故|A|=0.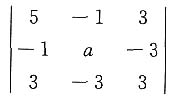 =3(2a-10)=0,得a=5,
=3(2a-10)=0,得a=5,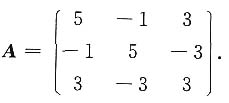
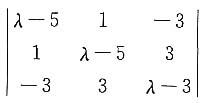 =λ(λ-4)(λ-9)=0,得λ1=0,λ2=4,λ3=9.
=λ(λ-4)(λ-9)=0,得λ1=0,λ2=4,λ3=9.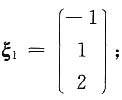 由(4E-A)X=0得
由(4E-A)X=0得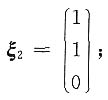
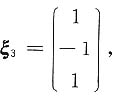 单位化得
单位化得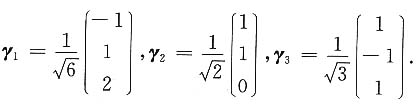
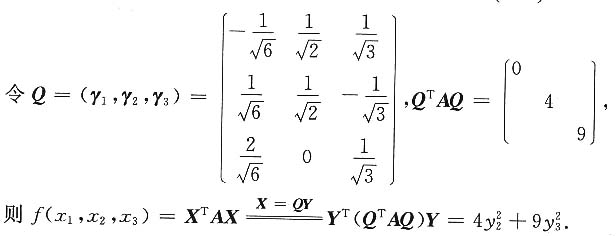
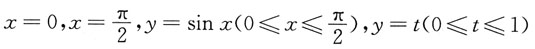 所围区域的面积为S(t),求S(t)的最大值与最小值.
所围区域的面积为S(t),求S(t)的最大值与最小值.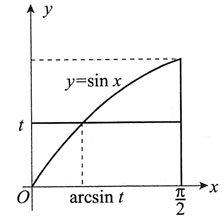
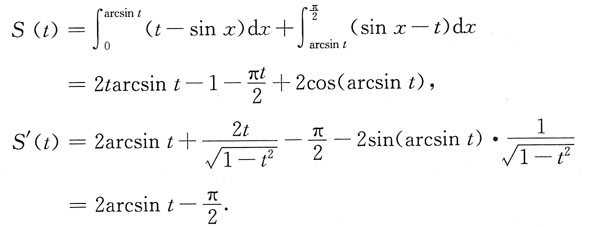
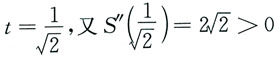 ,因此
,因此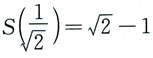 为极小值.又
为极小值.又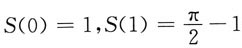 ,所以S(t)最大值为1,最小值为
,所以S(t)最大值为1,最小值为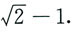
 ABAB=E
ABAB=E (E-AB)(E+AB)=O,
(E-AB)(E+AB)=O,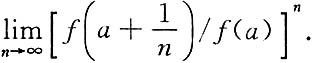
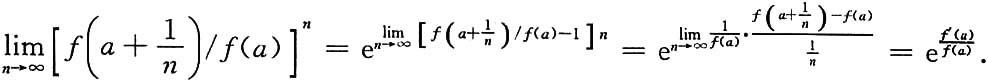
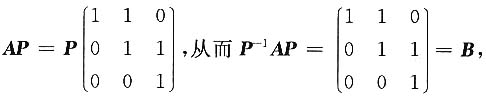
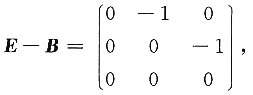

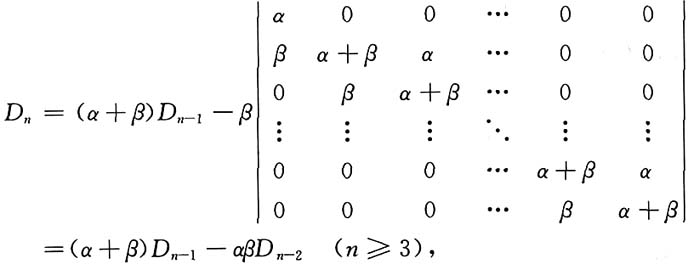
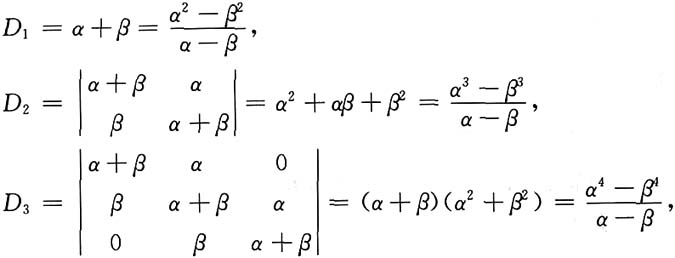
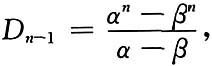 则有
则有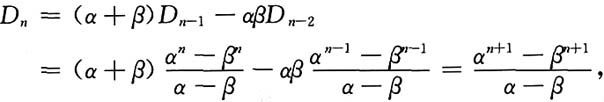
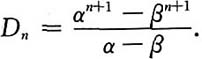
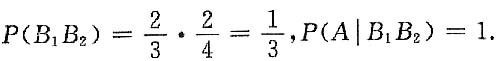
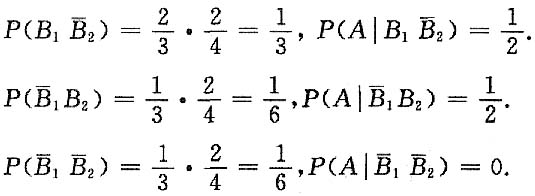
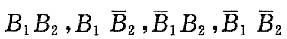 构成一个完备事件群.
构成一个完备事件群.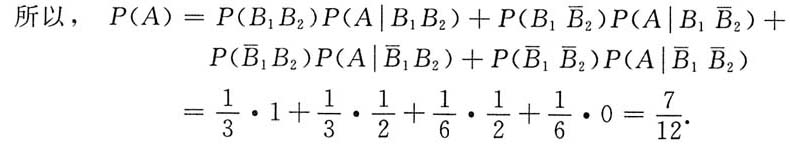
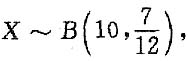
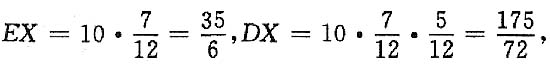
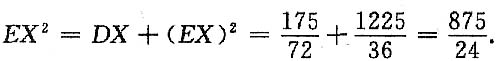
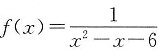 展开成(x-1)的幂级数.
展开成(x-1)的幂级数.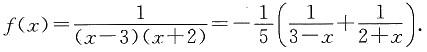
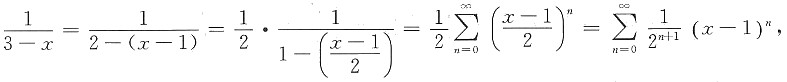
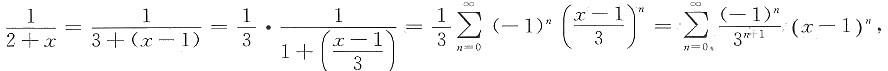
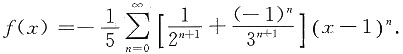
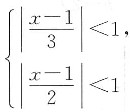 可知-1<x<3,故展开式成立的范围是(-1,3).
可知-1<x<3,故展开式成立的范围是(-1,3).