一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.3. 设X和Y分别表示扔n次硬币出现正面和反面的次数,则X,Y的相关系数为______.
A.-1
B.0
C.
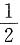
D.1
A B C D
A
[解析] 设正面出现的概率为p,则X~B(n,p),Y=n-X~B(n,1-p),E(X)=np,D(X)=np(1-p),E(Y)=n(1-p),D(Y)=np(1-p),Cov(X,Y)=Cov(X,n-X)=Cov(X,n)-Cov(X,X),
因为Cov(X,n)=E(nX)-E(n)E(X)=nE(X)-nE(X)=0,
CoV(X,X)=D(X)=np(1-p),所以
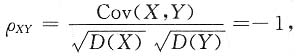
选A.
6. 设当x→0时,(1-cosx)ln(1+x
2)是比xsinx
m高阶的无穷小,而xsinx
m是比e
x2-1高阶的无穷小,则正整数m等于______.
A B C D
B
[考点] 无穷小阶的比较.
[解析] 利用无穷小阶的定义.
解:由条件知
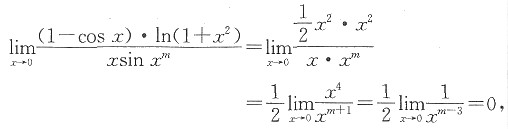
所以m<3,而
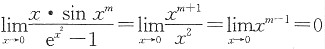
,所以m>1.
综上知正整数m=2.
故应选B.
7. 设总体X服从参数为λ(λ>0)的泊松分布,X
1,X
2,…,X
n为来自总体X的简单随机样本.记
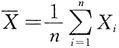
,
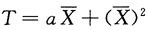
,其中a为常数.若E(T)=λ
2,则a=______.
A.
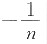
B.
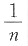
C.-1
D.1
A B C D
A
[考点] 统计量的数字特征.
[解析] 利用
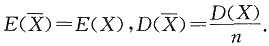
解:因为X服从泊松分布P(λ),则E(X)=D(X)=λ,
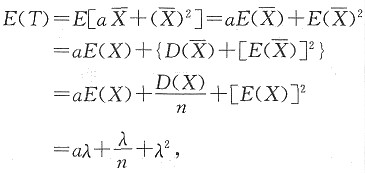
由E(T)=λ
2,可得
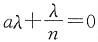
,则
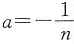
.
故应选A.
8. 设总体X服从正态分布N(0,σ
2)(σ
2已知),X
1,X
2,…,X
n是取自总体X的简单随机样本,S
2为样本方差,则______
A.
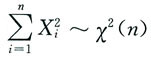
B.
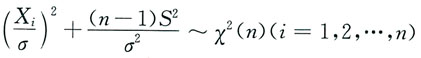
C.
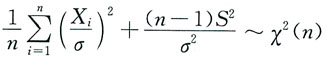
D.
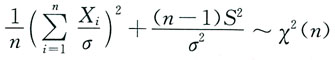
A B C D
二、填空题1. 设X,Y为随机变量,已知D(X)=25,D(Y)=36,X与Y的相关系数ρ
XY=0.4,则cov(2X-3Y,X-Y)=______.
98
[解析] 因为
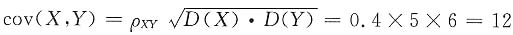
,则
cov(2X-3Y,X-Y)=2cov(X,X)-2cov(X,Y)-3cov(X,Y)+3cov(Y,Y)
=2D(X)+3D(Y)-5cov(X,Y)
=2×25+3×36-5×12=98.
2. 已知P(A)=0.5,P(B)=0.6,P(B|A)=0.4,则P{(A-B)|A∪B}=______.
[解析] 由题设可知,P(AB)=P(A)P(B|A)=0.5×0.4=0.2,于是
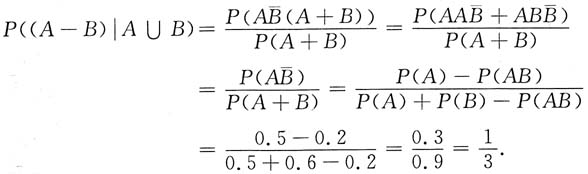
3. 微分方程y"-9y=e
3x的通解为______.
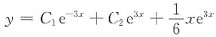
(C
1,C
2为任意常数)
[解析] 特征方程为,r
2=
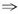
r
1=3,,r
2=-3.
故y"-9y=0的通解为y
1=C
1e
-3x+C
2e
3x(C
1,C
2为任意常数).
由于非齐次方程右端的非齐次项为e
3x,指数上的3为特征方程的单根,故特解设为y
*=Axe
3x代入原方程,可得
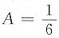
,
所以原方程的通解为
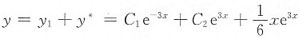
.
4. 设f(x)在区间[-π,π]上连续且满足f(x+π)=-f(x),则f(x)的傅里叶系数a
2n=______(n=1,2,…).
0
[解析]
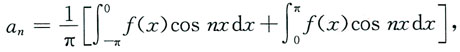
前一积分,令t=x+π,所以x=t-π,则
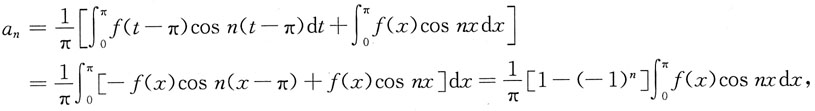
所以a
2n=O(n=0,1,2,…)
本题考查傅里叶系数.
5. 设总体X二阶矩存在,X
1,X
2,…,X
n是其简单样本,样本均值和方差分别为
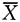
和S
2.如果X服从(-θ,θ)内均匀分布,θ>0,则θ的矩估计量为______.
[解析]
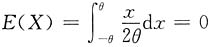
,期望为零,与θ无关,因此考虑方差
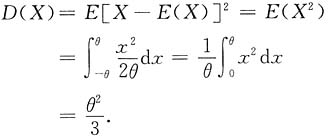
由矩估计方程D(X)=S
2,得
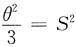
,解得θ的矩估计量为

6.
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.求下列各式的不定积分.1. ∫e
ex+xdx;
解:∫eex+xdx=∫eexd(ex)=eex+C.
2.
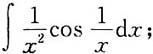
解:
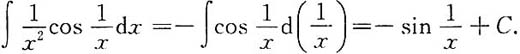
3. ∫x(1+x
2)
100dx;
解:
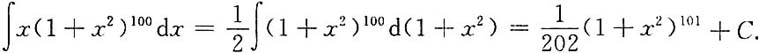
4.
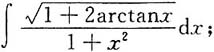
解:
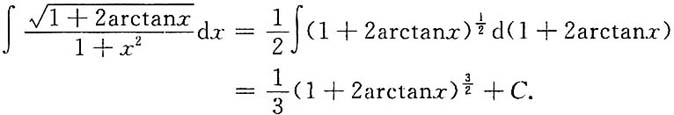
5.
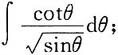
解:
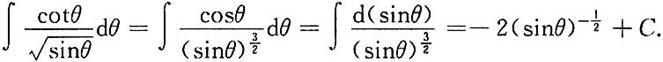
6.
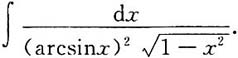
解:
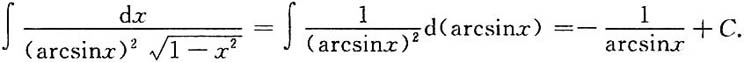
7. 设X,Y是独立同分布的离散型随机变量,分布律为
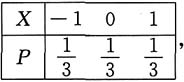
求矩阵

的秩为2的概率.
解:对A施行初等变换
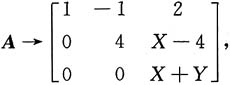
因为r(A)=2,所以X+Y=0.又X+Y的分布律为
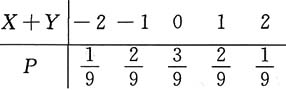
所以A的秩为2的概率为
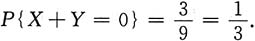
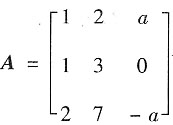 可经初等变换化为矩阵
可经初等变换化为矩阵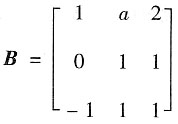
8. 求a;
解:A与B等价,则r(A)=r(B).
又
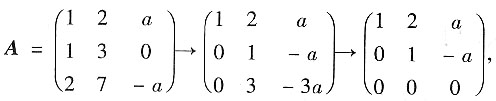
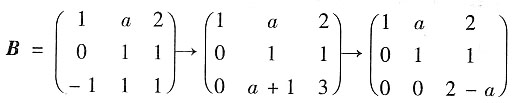
所以r(A)=r(B)=2,a=2.
9. 求满足AP=B的可逆矩阵P.
解:
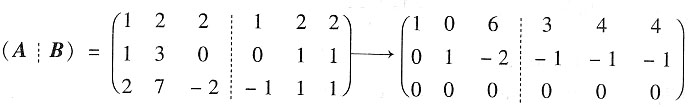
AP=B,
得

对P做初等变换
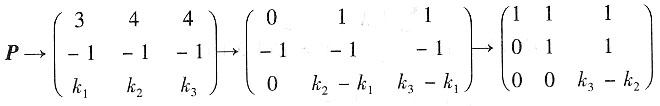
又P可逆,所以|P|≠0,即k
2≠k
3.
最终
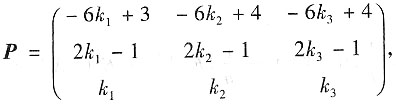
其中k
1,k
2,k
3为任意常数,且k
2≠k
3.

令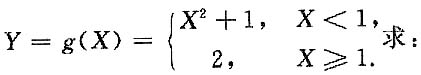
10. 求F
Y(y);
解:F
Y(y)=P{Y≤y}.
①当y<1时,F
Y(y)=P{Y≤y}=0;
②当y≥10时,F
Y(y)=P{Y≤y}=1;
③当1≤y<2时,

④当2≤y<10时,

∴
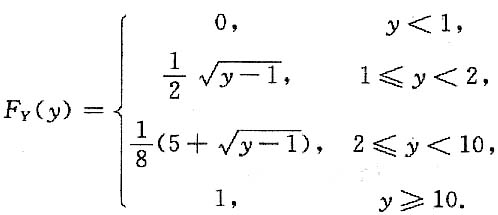
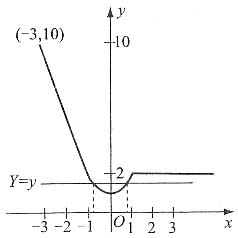
图1
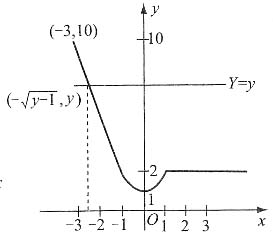
图2
11. Cov(X,Y).
解:
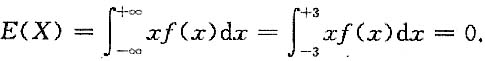
(f(x)为偶函数)
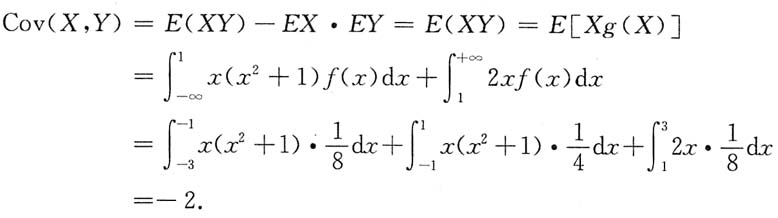
12. 设点M(ξ,η,ζ)是椭球面
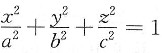
上第一卦限中的点,S是该椭球面在点M处的切平面被三个坐标面所截得的三角形的上侧.求点(ξ,η,ζ)使曲面积分
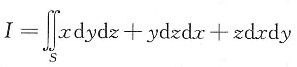
为最小,并求此最小值.
解:曲面
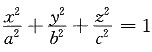
上点M(ξ,η,ζ)处的法向量为
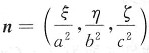
,切平面方程是
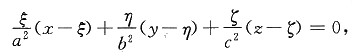
化简即得
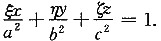
该切平面被三坐标面截得的三角形在xOy平面上的投影区域为
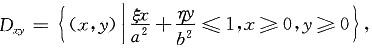
从而
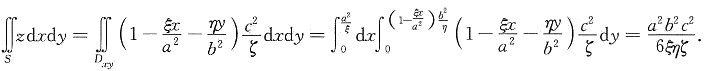
所以
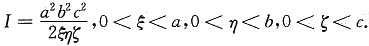
求I的最小值等价于求ω=ξηζ,0<ξ<a,0<η<b,0<ζ<c的最大值,约束条件是
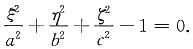
由拉格朗日乘数法得
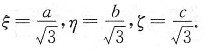
显然,当ξ=a或ξ=0时,ω最小,故当

时,ω最大,I的最小值为
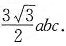
13. 设对于在x>0上可微的函数f(x)及其反函数g(x),满足方程
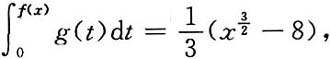
求解f(x).
解:方程两边对x求导,得
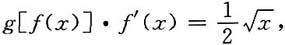
即
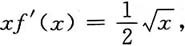
当x>0时,有
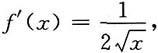
积分得
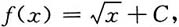
又当f(x)=0时,
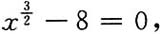
x=4,即f(4)=0,C=-2,所以
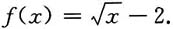
14. 设∑为x
2+y
2+z
2=1(2≥0)的外侧,连续函数f(x,y),)满足f(x,y)=2(x-y)
2+
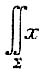
(z
2+e
z)dydz+y(z
2+e
z)dzdx+[zf(x,y)-2e
z]dxdy,求f(x,y).
解:设
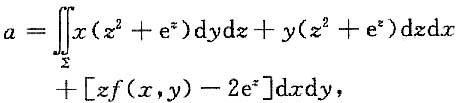
则f(x,y)=2(x-y)
2+a,设D为xOy平面上的圆x
2+y
2≤1,∑
下为D的下侧.
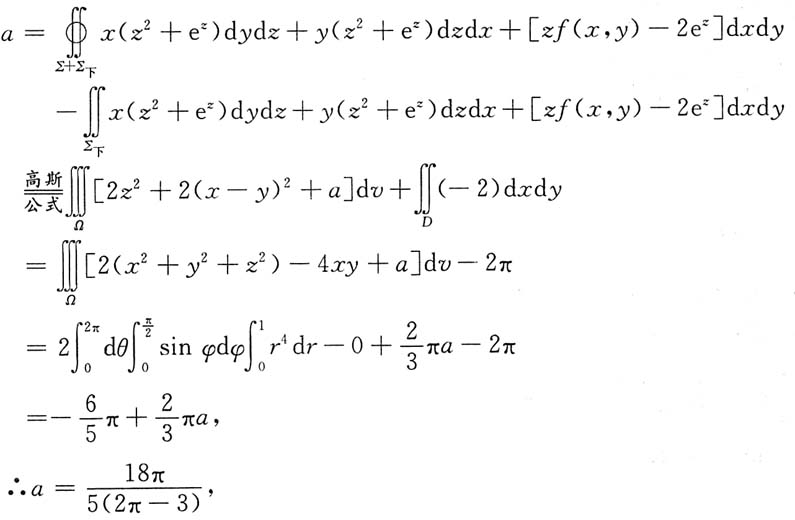
于是,
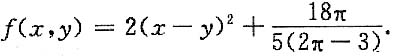
15. 设f"(x)<0,f(0)=0,证明:对任何x
1>0,x
2>0有
f(x
1+x
2)<f(x
1)+f(x
2).
证明:由拉格朗日中值定理有
f(x1)=f(x1)-f(0)=x1f'(ξ1),0<ξ1<x1,
f(x1+x2)-f(x2)=x1f'(ξ2),x2<ξ2<x1+x2,
不妨设x1≤x2,从而ξ1<ξ2,因为f"(x)<0,所以f'(x)“↘”,又因为f'(ξ2)<f'(ξ1),
故f(x1+x2)-f(x2)<x1f'(ξ1)=f(x1),
即f(x1+x2)<f(x1)+f(x2).
[解析] 因为f(x)可导,又f(0)=0,可知一定可用拉格朗日中值定理证明.
16. 设随机变量X,Y相互独立且都服从N(μ,σ
2)分布,令Z=max(X,Y),求E(Z).
解:因为X,Y都服从N(μ,σ
2)分布,所以
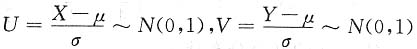
,
且U,V相互独立,则X=σU+μ,Y=σV+μ,故Z=max(X,Y)=σmax(U,V)+μ,
由U,V相互独立得(U,V)的联合密度函数为
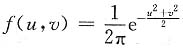
(-∞<u,v<+∞).
于是E(Z)=σE[max(U,V)]+μ。
而
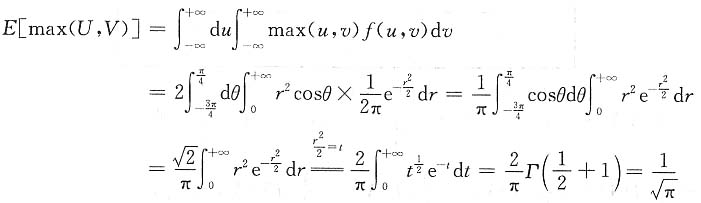
故
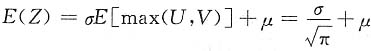
.
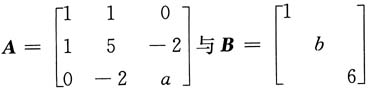 相似,则______
相似,则______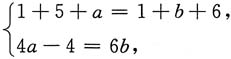
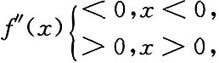 则其图形(如图所示)是
则其图形(如图所示)是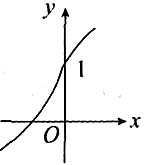
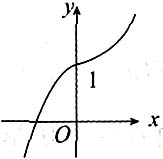
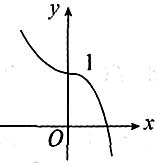
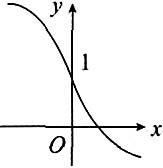
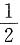
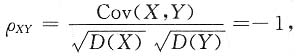 选A.
选A.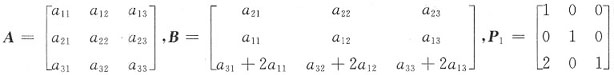 ,
,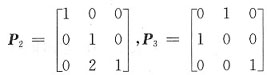 ,则B=______
,则B=______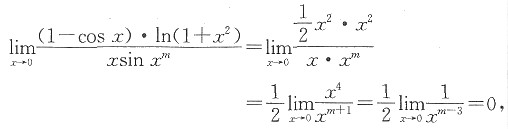
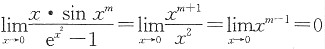 ,所以m>1.
,所以m>1.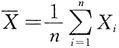 ,
,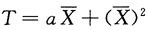 ,其中a为常数.若E(T)=λ2,则a=______.
,其中a为常数.若E(T)=λ2,则a=______.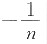
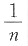
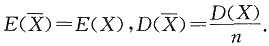
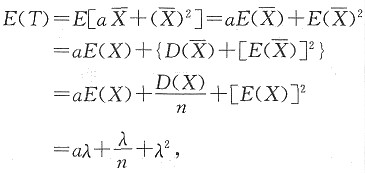
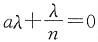 ,则
,则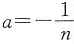 .
.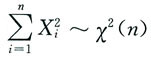
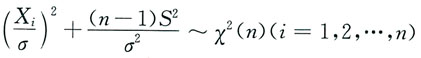
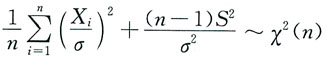
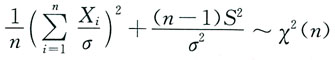
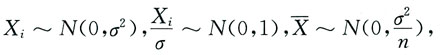
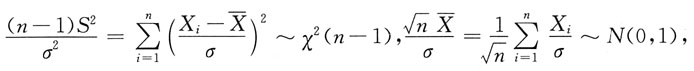
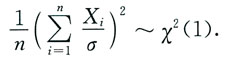
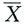 与S2独立,故有
与S2独立,故有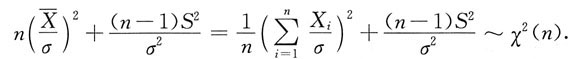
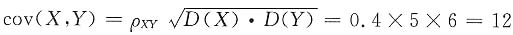 ,则
,则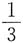
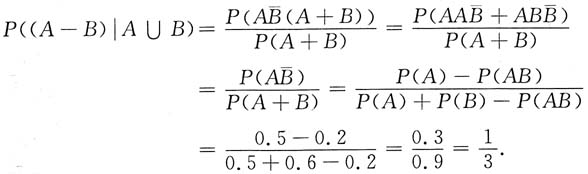
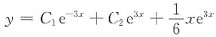 (C1,C2为任意常数)
(C1,C2为任意常数)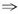 r1=3,,r2=-3.
r1=3,,r2=-3.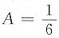 ,
,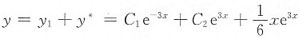 .
.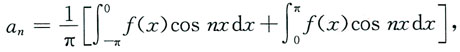
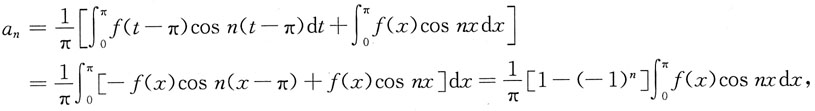
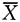 和S2.如果X服从(-θ,θ)内均匀分布,θ>0,则θ的矩估计量为______.
和S2.如果X服从(-θ,θ)内均匀分布,θ>0,则θ的矩估计量为______.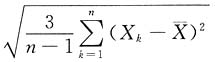
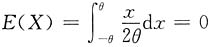 ,期望为零,与θ无关,因此考虑方差
,期望为零,与θ无关,因此考虑方差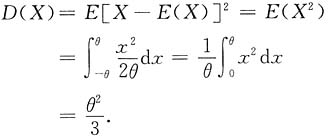
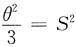 ,解得θ的矩估计量为
,解得θ的矩估计量为
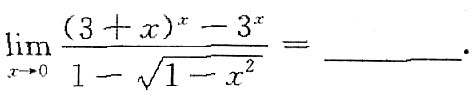
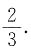
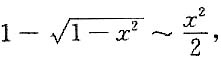
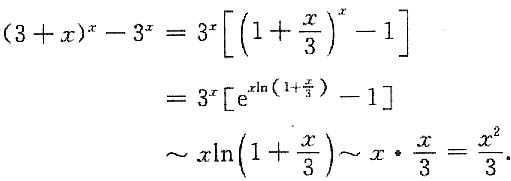
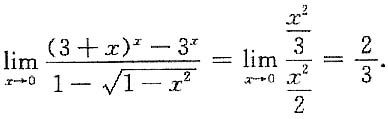
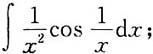
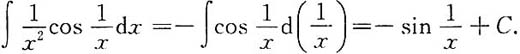
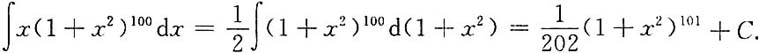
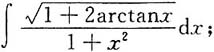
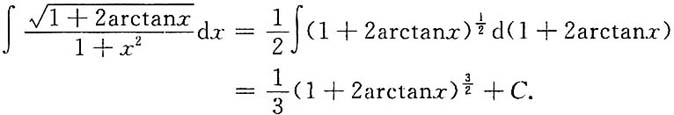
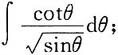
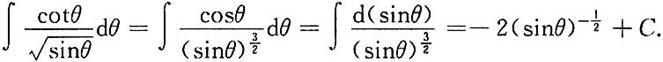
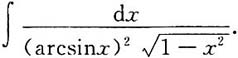
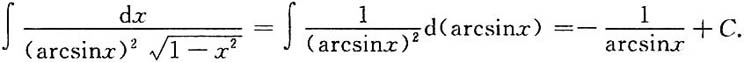
 求矩阵
求矩阵 的秩为2的概率.
的秩为2的概率.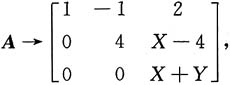
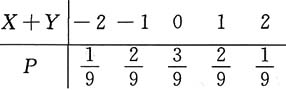
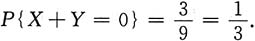
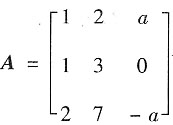 可经初等变换化为矩阵
可经初等变换化为矩阵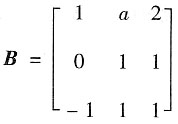
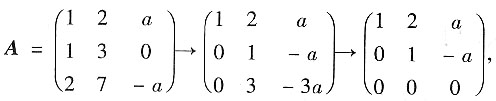
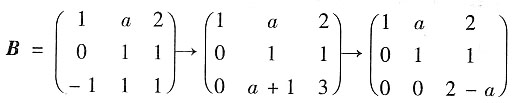
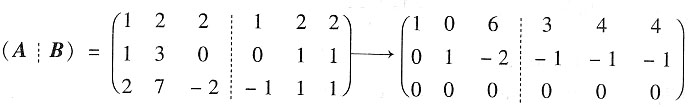

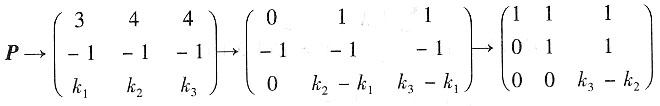
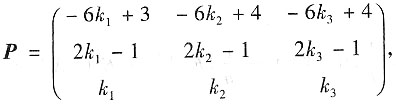 其中k1,k2,k3为任意常数,且k2≠k3.
其中k1,k2,k3为任意常数,且k2≠k3.
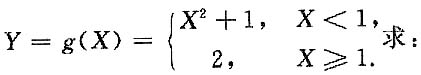


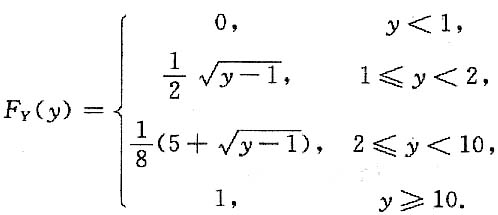


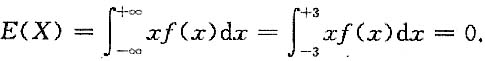 (f(x)为偶函数)
(f(x)为偶函数)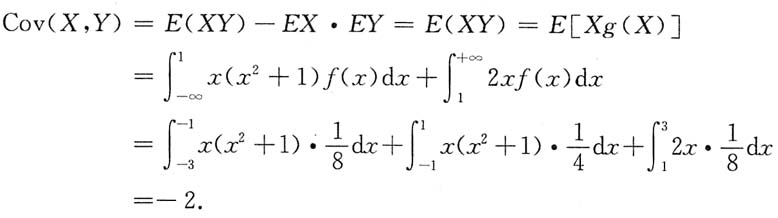
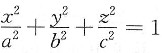 上第一卦限中的点,S是该椭球面在点M处的切平面被三个坐标面所截得的三角形的上侧.求点(ξ,η,ζ)使曲面积分
上第一卦限中的点,S是该椭球面在点M处的切平面被三个坐标面所截得的三角形的上侧.求点(ξ,η,ζ)使曲面积分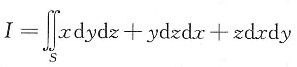
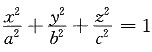 上点M(ξ,η,ζ)处的法向量为
上点M(ξ,η,ζ)处的法向量为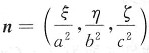 ,切平面方程是
,切平面方程是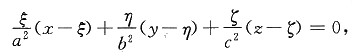
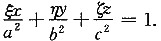
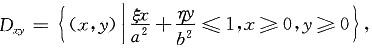
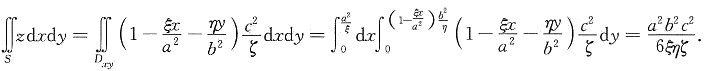
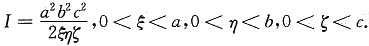
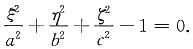
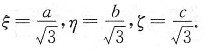
 时,ω最大,I的最小值为
时,ω最大,I的最小值为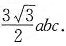
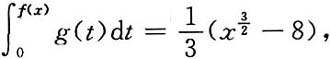
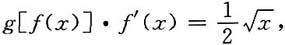 即
即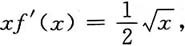
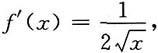 积分得
积分得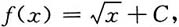
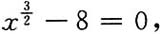 x=4,即f(4)=0,C=-2,所以
x=4,即f(4)=0,C=-2,所以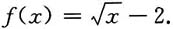
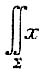 (z2+ez)dydz+y(z2+ez)dzdx+[zf(x,y)-2ez]dxdy,求f(x,y).
(z2+ez)dydz+y(z2+ez)dzdx+[zf(x,y)-2ez]dxdy,求f(x,y).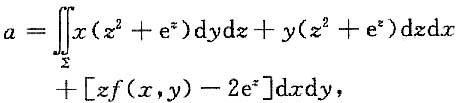
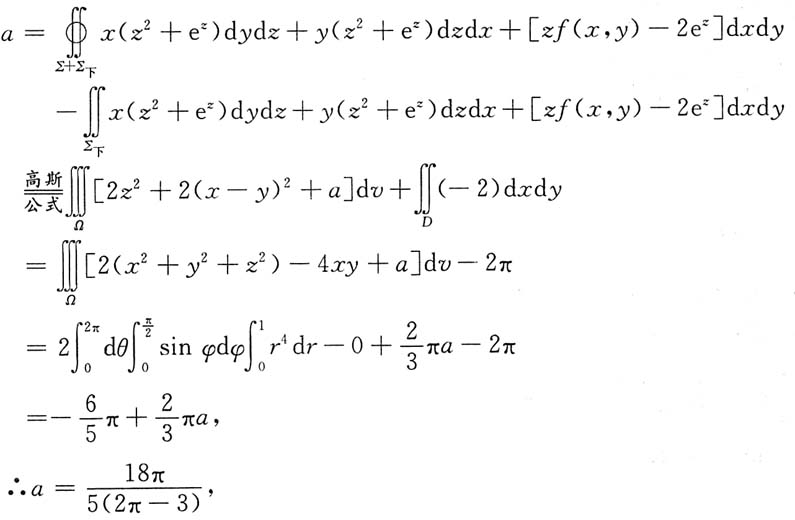
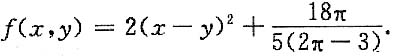
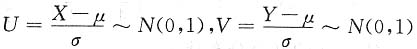 ,
,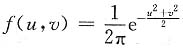 (-∞<u,v<+∞).
(-∞<u,v<+∞).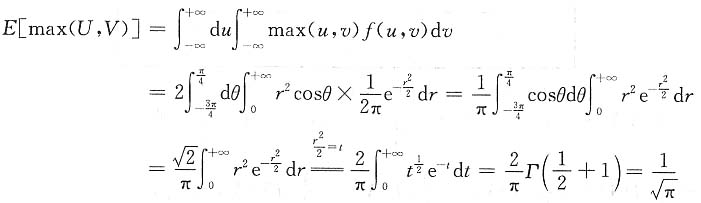
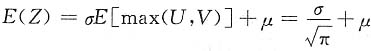 .
.