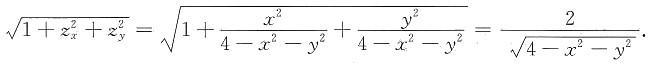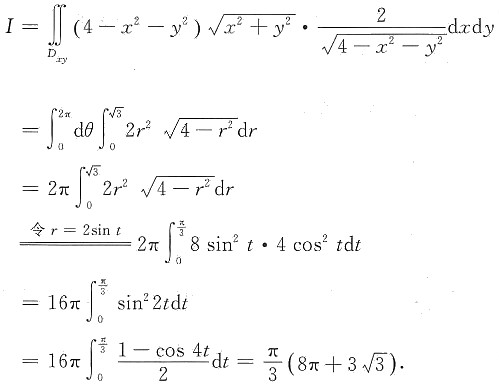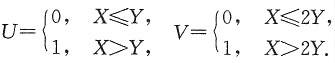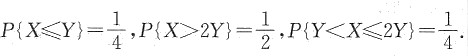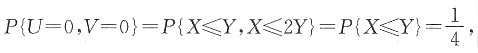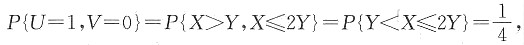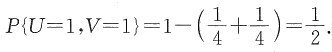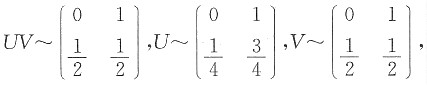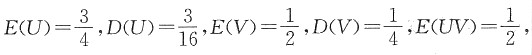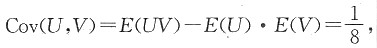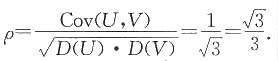DxxwdnObakTOJfXRFbvZ7AhKrycXEPNcFpxIdeYPBQ7ExPtMN4gn+g==
下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设f(x,y)连续,且
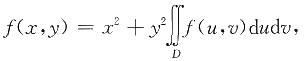
其中D={(x,y)|1≤x
2+y
2≤9},则f(x,y)=
A.x
2.
B.x
2+y
2.
C.
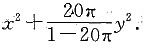
D.
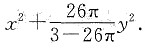
A B C D
C
[解析] 设
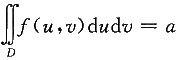
,则f(x,y)=x
2+ay
2.于是
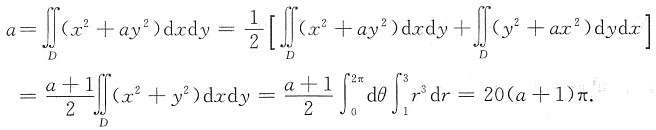
解之得
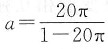
,故
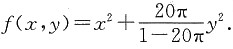
4. 设随机变量X的分布函数为
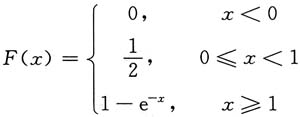
,则P{x=0}=______
A.0.
B.
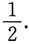
C.

D.1-e
-1.
A B C D
B
[解析] 由分布函数的定义得
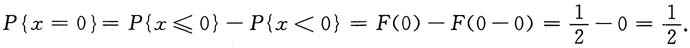
5. 设X
1,X
2,…,X
n(n>2)为来自总体N(0,1)的简单随机样本,
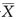
为样本均值.记Y
i=
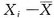
,i=1,2,…,n.则______
A.
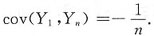
B.
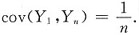
C.
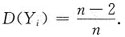
D.
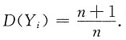
A B C D
A
[解析] 由已知得E(X
i)=0,D(X
i)=1,i=1,2,…,n,则
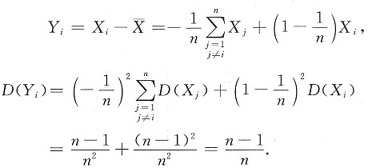
排除选项C和D.
因X
1,X
2,…,X
n相互独立,而独立的两个随机变量协方差等于零,于是有
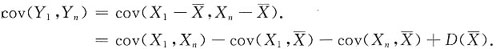
而
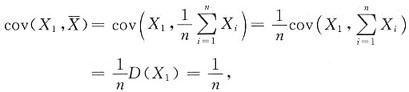
类似地
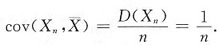
又因为
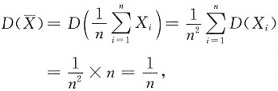
所以有
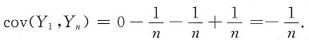
6. 下列命题正确的是______
A.
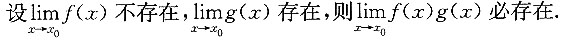
B.
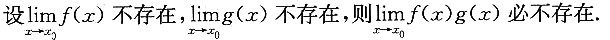
C.
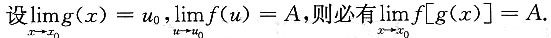
D.
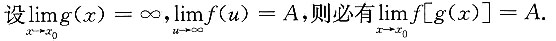
A B C D
D
[解析]
法一 举例说明A,B,C都不正确.
A.的反例:
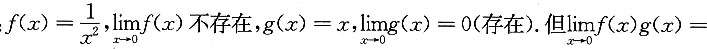
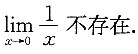
B.的反例:
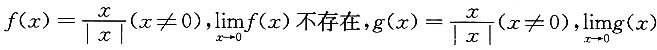
也不存在.但
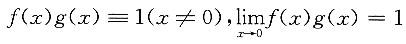
(存在).
C的反例:
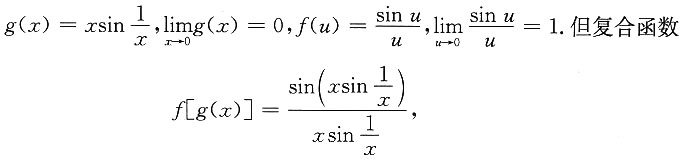
不论δ>0多么小,在x=0的δ去心邻域
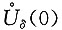
内,f[g(x)]在无穷多个点上(例如
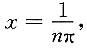
n∈Z且充分大)没有定义,故C.不成立.选D.
法二 证明D.正确.由
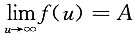
知,对于任给的ε>0,存在M>0,当|u|>M时,有|f(u)-A|<<ε.又因
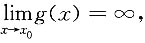
故对于上述M>0,存在δ>0,当0<|x-x
0|<δ时,|g(x)|>M.将k述两项联合起来推知,对于任给的ε>0,存存δ>0,当0<|x-x
0|<δ时,有|f[g(x)]-A|<ε,即
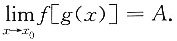
选D.
7. 下列二次型中,正定二次型是______
- A.f1(x1,x2,x3,x4)=(x1-x2)2+(x2-x3)2+(x3-x4)2+(x4-x1)2.
- B.f2(x1,x2,x3,x4)=(x1+x2)2+(x2+x3)2+(x3+x4)2+(x4+x1)2.
- C.f3(x1,x2,x3,x4)=(x1-x2)2+(x2+x3)2+(x3-x4)2+(x4+x1)2.
- D.f4(x1,x2,x3,x4)=(x1-x2)2+(x2+x3)2+(x3+x4)2+(x4+x1)2.
A B C D
D
[解析] 法一 A存在x
1=(1,1,1,1)
T,使得f
1(x
1)=0,f
1不正定.
B存在x
2=(1,-1,1,-1)
T,使得f
2(x
2)=0,f
2不正定.
C存在x
3=(1,1,-1,-1)
T,使得f
3(x
3)=0,f
3不正定.
由排除法知,应选D.
法二 对D,f
4(x
1,x
2,x
3,x
4)=(x
1-x
2)
2+(x
2+x
3)
2+(x
3+x
4)
2+(x
4+x
1)
2,
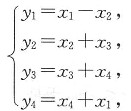
即

其中
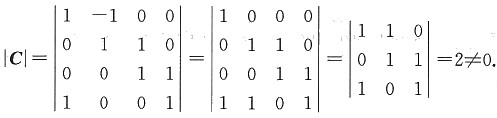
故x=C
-1y是可逆线性变换,则由

知,f
4是正定二次型.
法三 f
4(x
1,x
2,x
3,x
4)=(x
1-x
2)
2+(x
2+x
3)
2+(x
3+x
4)
2+(x
4+x
1)
2 
其中
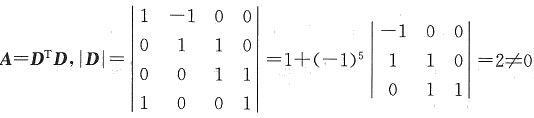
,D是可逆矩阵.
故知A=D
TD是正定矩阵,f
4是正定二次型.
法四 写出各二次型的对应矩阵,用顺序主子式是否都大于零来判别,请读者自行计算.
8. 设X,Y为两个随机变量,其中E(X)=2,E(Y)=-1,D(X)=9,D(Y)=16,且X,Y的相关系数为ρ=
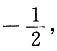
由切比雪夫不等式得P{|X+Y-1|≤10}≥______.
A.
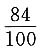
B.
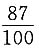
C.
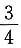
D.
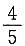
A B C D
B
[解析] 令Z=X+Y,则E(Z)=E(X)+E(Y)=1,
D(Z)=D(X+Y)=D(X)+D(Y)+2Cov(X,Y)=13,
则P{|X+Y-1|≤10}=P{|Z-E(Z)|≤10}≥
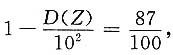
选B.
二、填空题1.
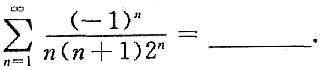
2. 若对任意的n×1矩阵X,均有AX=0,则A=______.
3. 将一均匀的骰子连续扔六次,所出现的点数之和为X,用切比雪夫不等式估计P(14<X<28)=______.
[解析] 设X
i为第i次的点数(i=1,2,3,4,5,6),则
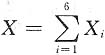
,其中
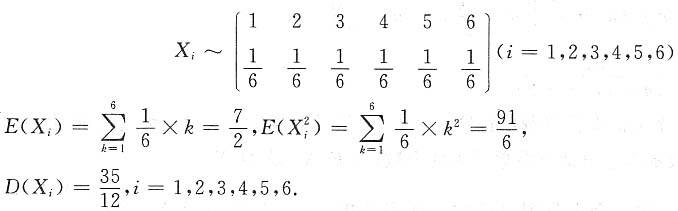
则
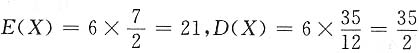
,由切比雪夫不等式,有
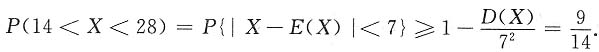
4. 设A为三阶实对称矩阵,
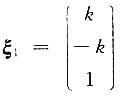
为方程组AX=0的解,
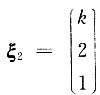
为方程组(2E-A)X=0的一个解,|E+A|=0,则A=______.
[解析] 显然
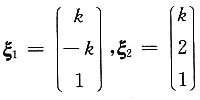
为A的特征向量,其对应的特征值分别为λ
1=0,λ
2=2,因为A为实对称阵,所以
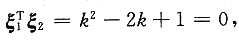
解得k=1,于是
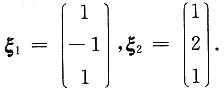
又因为|E+A|=0,所以λ
3=-1为A的特征值,令λ
3=-1对应的特征向量为
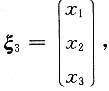

5. 设y(x)≠0且为连续函数,
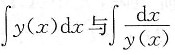
分别为y(x)与
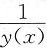
的某两个原函数,又设

,且y(0)=1,并设

则y(x)=______.
e-x
[解析] 由
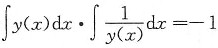
,有
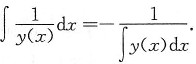
两边对x求导,得
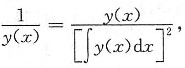
所以
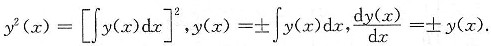
所以y=Ce
±x.由题设y(0)=1,知C=1.又因为
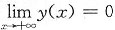
,故“±”取“-”.所以y=e
-x.
6. 设函数y=y(x)在(0,+∞)上满足
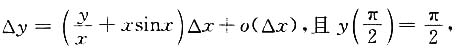
则y(x)=______.
x(1-cosx)
[解析] 由可微的定义,函数y=y(x)在(0,+∞)内可微,
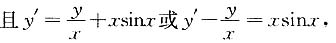
由一阶非齐次线性微分方程的通解公式得
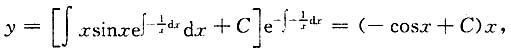
由
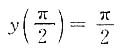
得C=1,所以y=x(1-cosx).
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.设X1,X2,…,Xn(n>2)相互独立且都服从N(0,1),Yi=Xi-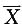 (i=1,2,…,n).求
(i=1,2,…,n).求1. D(Y
i)(i=1,2,…,n);
解:D(Y
i)=Cov(Y
i,Y
i)
=D(X
i)+D(
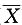
)-2Cov(X
i,
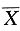
)

2. Cov(Y
1,Y
n);
解:Cov(Y
1,Y
n)
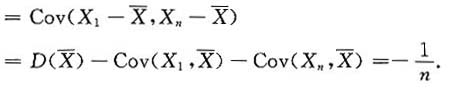
3. P{Y
1+Y
n≤0}.
解:Y
1+Y
n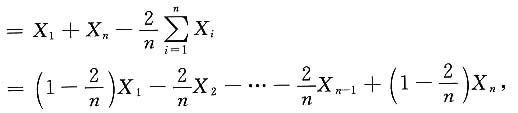
因为X
1,X
2,…,X
n独立且都服从正态分布,所以Y
1+Y
n服从正态分布,
E(Y
1+Y
n)=0
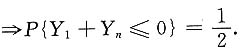
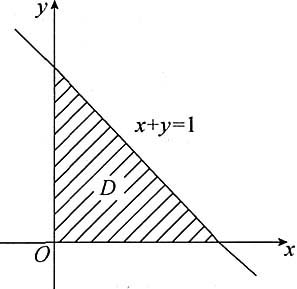
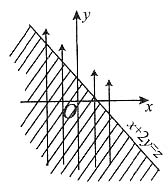
4. 求由下列曲面所围成的形体的体积:z=x+y,z=xy,x+y=1,x=0,y=0.
解:显然,由以上曲面所围的空间形体在xOy坐标上的投影是由x+y=1及x,y轴所围成的三角形,如图所示.
因为0≤x≤1,0≤y≤1,因而x+y≥xy,
所以所求体积
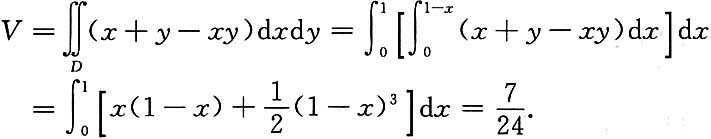
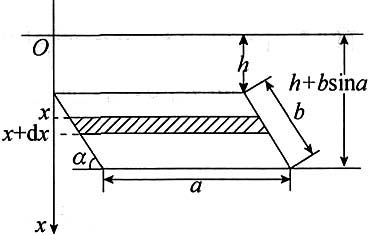
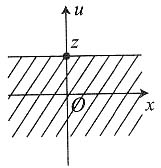
5. 边长为a和b的矩形薄板(a>b),放置于与液面成α角的液体内,长边平行于液面,位于深h处,设液体的比重为σ,求薄板所受的压力P.
解:建立坐标,如图所示,当x取增量dx时,薄板对应的宽度为
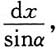
于是图中阴影部分的面积为
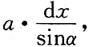
这小条所受液体的静压力为
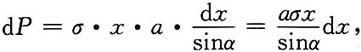
整块薄板所受压力为

6. 设f(x,y)=x
3+y
3-3x
2-3y
2,求f(x,y)的极值及其在x
2+y
2≤16上的最大值.
解:根据题意可得
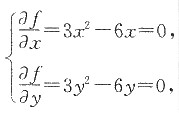
解得x
1=0,x
2=2,y
1=0,y
2=2.
即共有4个极值可疑点:(0,0),(0,2),(2,0),(2,2).
又因为
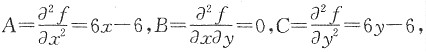
则在点(0,0)处,
B
2-AC=0-(-6)×(-6)=-36<0且A=-6<0.
所以点(0,0)是一个极大值点且极大值为f(0,0)=0.
同理,f(2,2)=-8是一个极小值;而f(0,2)与f(2,0)不是极值.
由上面讨论可知,f(x,y)在闭域D上的最大值,若在D内达到,必是在(0,0)点取得,但也可能在D的边界上,故建立拉格朗日函数.
令
L(x,y,λ)=x
3+y
3-3x
2-3y
2+λ(x
2+y
2-16),
则有
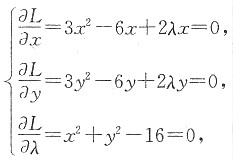
解得:x=0,y=4或x=4,y=0或
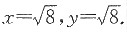
因此f(x,y)在D上的最大值为
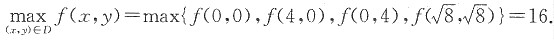
[考点] 多元函数的极值、最值.
[解析] 先求出函数f(x,y)在区域D:x2+y2≤16内的极值可疑点(xi,yi)(i=1,2,…,m);再利用极值的充分判别法判断每个点是否为极值点,若是极值点,则求出对应的极值;最后由拉格朗日乘数法求得f(x,y)在D的边界上的可疑极值,将以上所得函数值进行比较,便可得到结果.
8. 求E(Z),D(Z).
解:
又X,Y相互独立,
∴EZ=E(X+2Y)=EX+2EY=1+1=2。
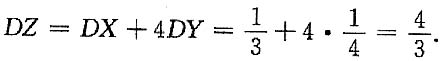
9. 证明由方程u=y+xφ(u)确定的函数u=u(x,y)满足方程
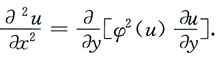
解:方程u=y+xφ(u)两边对x求偏导数,得

上式两边对x再求一次偏导数,得
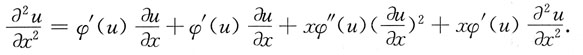
因此

另一方面
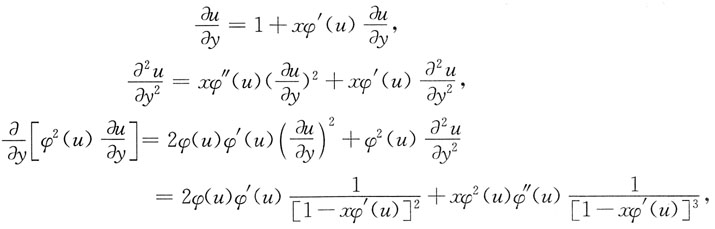
从而
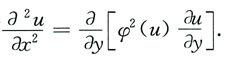
10. 已知△ABC的面积为S,三边长分别为a,b,c.在该三角形内求一点P,使该点到△ABC三边的距离的乘积为最大.并求出乘积最大时的这三个距离及此乘积的最大值.
解:设点P到边长分别为a,b,c的边的距离分别为x,y,z.于是
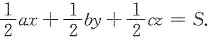
即ax+by+cz-2S=0.
令F(x,y,z,λ)=xyz+λ(ax+by+cz-2S),
由拉格朗日乘数法,

解得

当点P在三角形的边上时,xyz=0.而P在三角形内部时,xyz>0.所以当点P在三角形内部时,乘积xyz有最大值.所以当
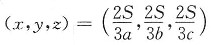
时,xyz最大,最大值为
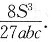
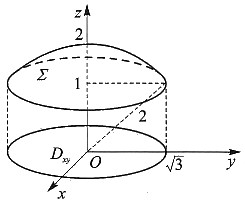
11. 计算曲面积分
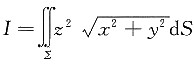
,其中Σ为球面x
2+y
2+z
2=4在z≥1的部分.
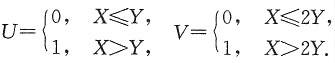
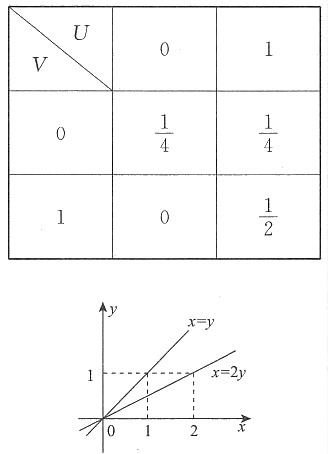
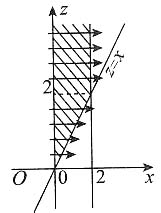
12. 求U和V的联合分布;
解:如图所示,由题设可得
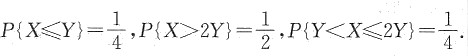
由(U,V)有四个可能值:(0,0),(0,1),(1,0),(1,1),则
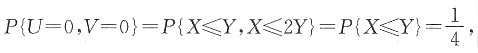
P{U=0,V=1}=P{X≤Y,X>2Y}=0,
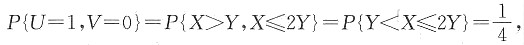
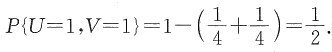
故U和V的联合分布为
13. 求U和V的相关系数ρ.
[考点] 考查二维离散型随机变量的分布及数字特征.
[解析] 由均匀分布求出(U,V)的分布律,然后求相关系数.
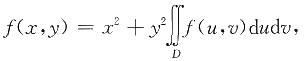 其中D={(x,y)|1≤x2+y2≤9},则f(x,y)=
其中D={(x,y)|1≤x2+y2≤9},则f(x,y)=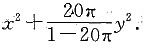
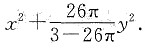
 ,则f(x,y)=x2+ay2.于是
,则f(x,y)=x2+ay2.于是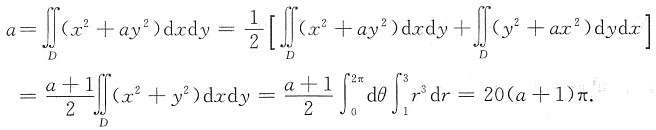
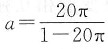 ,故
,故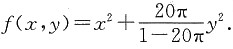
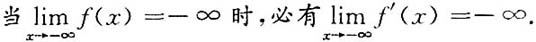
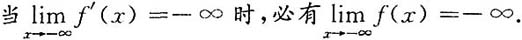
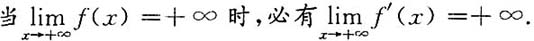
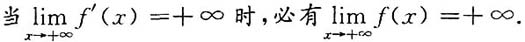
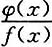 必有间断点.
必有间断点.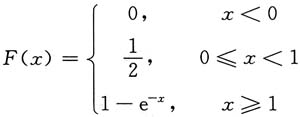 ,则P{x=0}=______
,则P{x=0}=______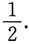

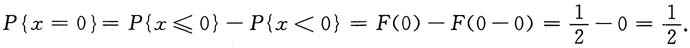
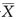 为样本均值.记Yi=
为样本均值.记Yi=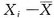 ,i=1,2,…,n.则______
,i=1,2,…,n.则______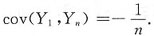
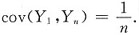
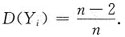
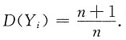
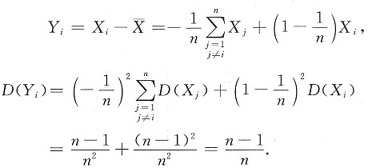
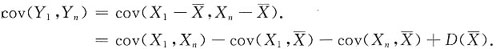
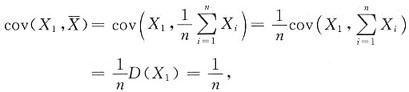
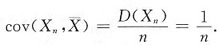
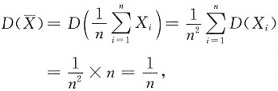
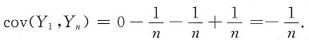
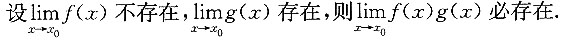
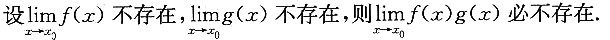
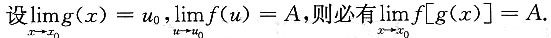
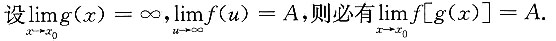
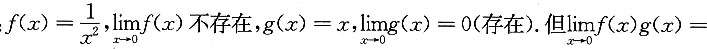
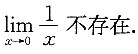
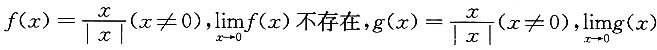 也不存在.但
也不存在.但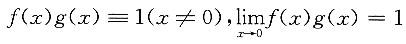 (存在).
(存在).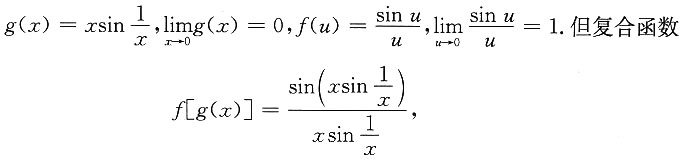
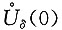 内,f[g(x)]在无穷多个点上(例如
内,f[g(x)]在无穷多个点上(例如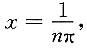 n∈Z且充分大)没有定义,故C.不成立.选D.
n∈Z且充分大)没有定义,故C.不成立.选D.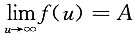 知,对于任给的ε>0,存在M>0,当|u|>M时,有|f(u)-A|<<ε.又因
知,对于任给的ε>0,存在M>0,当|u|>M时,有|f(u)-A|<<ε.又因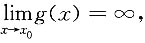 故对于上述M>0,存在δ>0,当0<|x-x0|<δ时,|g(x)|>M.将k述两项联合起来推知,对于任给的ε>0,存存δ>0,当0<|x-x0|<δ时,有|f[g(x)]-A|<ε,即
故对于上述M>0,存在δ>0,当0<|x-x0|<δ时,|g(x)|>M.将k述两项联合起来推知,对于任给的ε>0,存存δ>0,当0<|x-x0|<δ时,有|f[g(x)]-A|<ε,即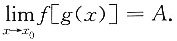
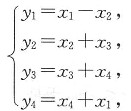 即
即
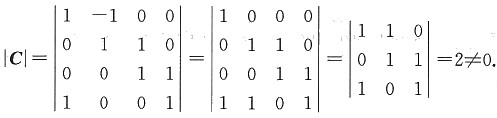
 知,f4是正定二次型.
知,f4是正定二次型.
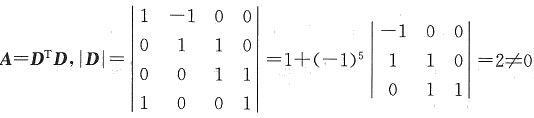 ,D是可逆矩阵.
,D是可逆矩阵.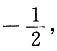 由切比雪夫不等式得P{|X+Y-1|≤10}≥______.
由切比雪夫不等式得P{|X+Y-1|≤10}≥______.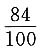
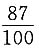
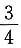
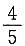
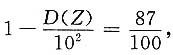 选B.
选B.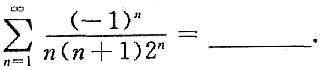
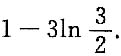

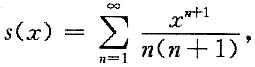 收敛域为[-1,1],
收敛域为[-1,1],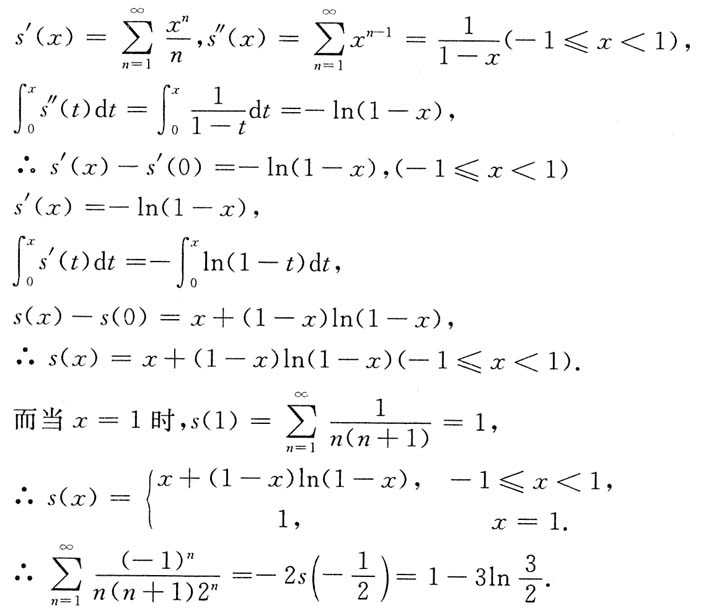
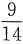
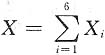 ,其中
,其中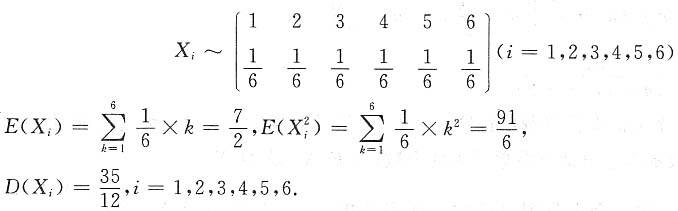
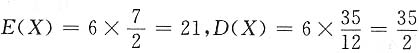 ,由切比雪夫不等式,有
,由切比雪夫不等式,有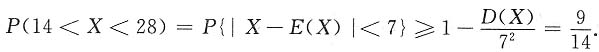
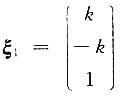 为方程组AX=0的解,
为方程组AX=0的解,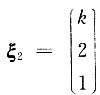 为方程组(2E-A)X=0的一个解,|E+A|=0,则A=______.
为方程组(2E-A)X=0的一个解,|E+A|=0,则A=______.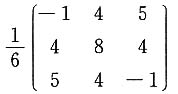
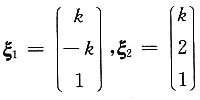 为A的特征向量,其对应的特征值分别为λ1=0,λ2=2,因为A为实对称阵,所以
为A的特征向量,其对应的特征值分别为λ1=0,λ2=2,因为A为实对称阵,所以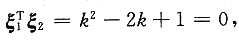 解得k=1,于是
解得k=1,于是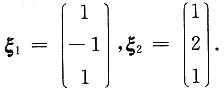


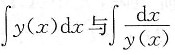 分别为y(x)与
分别为y(x)与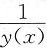 的某两个原函数,又设
的某两个原函数,又设 ,且y(0)=1,并设
,且y(0)=1,并设 则y(x)=______.
则y(x)=______.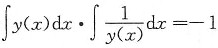 ,有
,有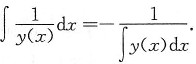
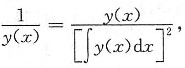
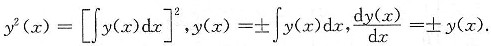
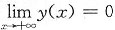 ,故“±”取“-”.所以y=e-x.
,故“±”取“-”.所以y=e-x.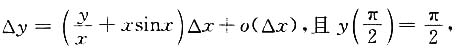 则y(x)=______.
则y(x)=______.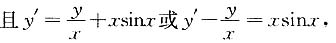 由一阶非齐次线性微分方程的通解公式得
由一阶非齐次线性微分方程的通解公式得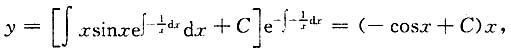
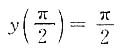 得C=1,所以y=x(1-cosx).
得C=1,所以y=x(1-cosx). (i=1,2,…,n).求
(i=1,2,…,n).求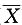 )-2Cov(Xi,
)-2Cov(Xi,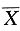 )
)
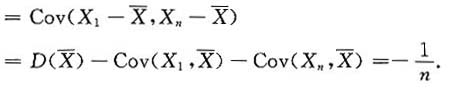
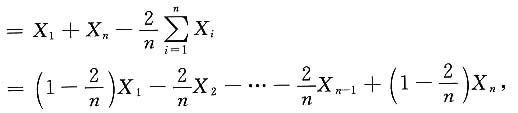
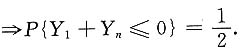
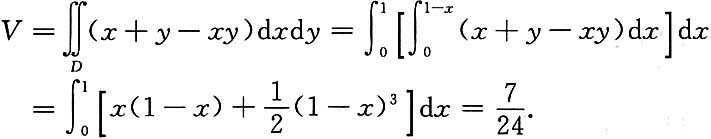
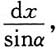 于是图中阴影部分的面积为
于是图中阴影部分的面积为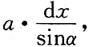 这小条所受液体的静压力为
这小条所受液体的静压力为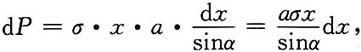

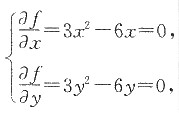
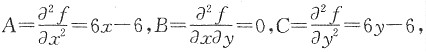
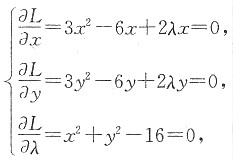
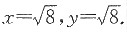
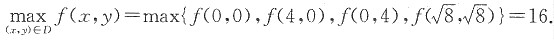
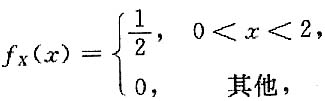
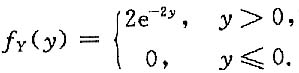
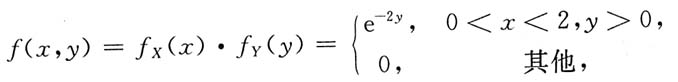
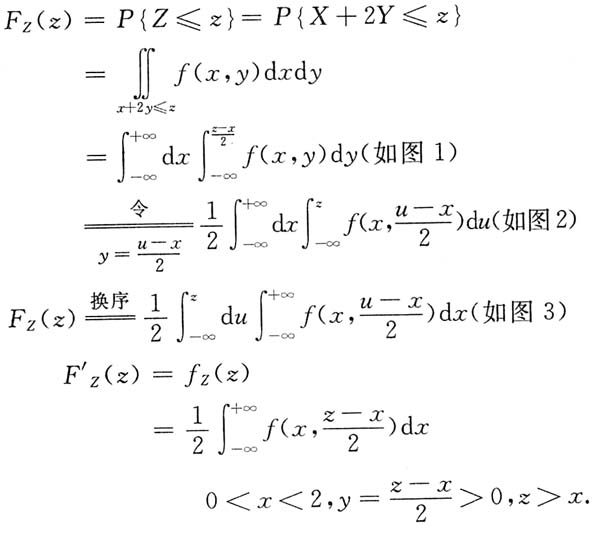
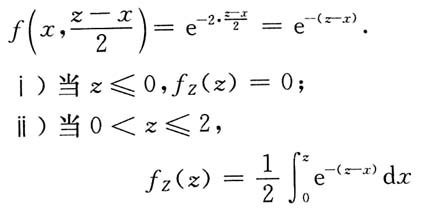
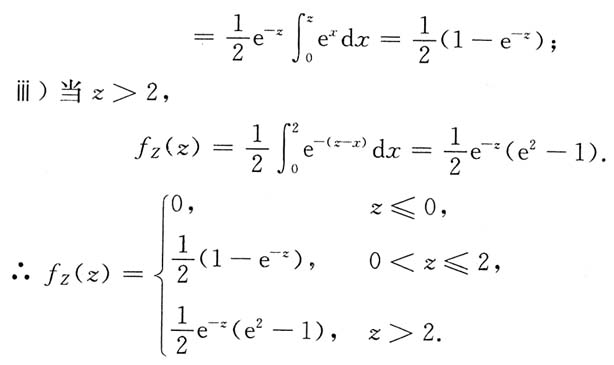
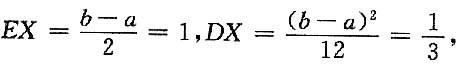
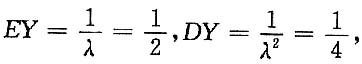
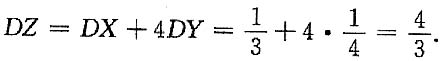
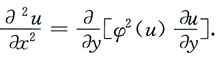

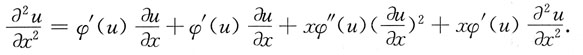

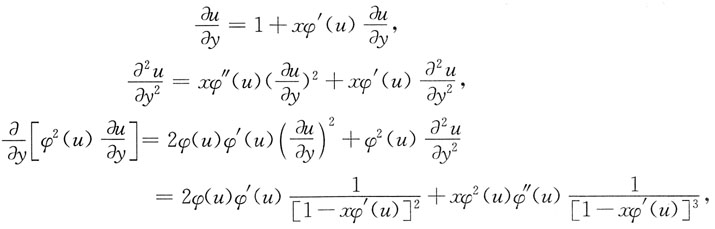
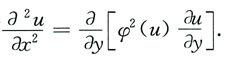
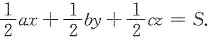


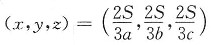
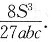
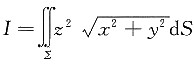 ,其中Σ为球面x2+y2+z2=4在z≥1的部分.
,其中Σ为球面x2+y2+z2=4在z≥1的部分.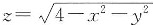 ,有
,有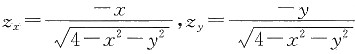 ,则
,则