一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设A,B为n阶矩阵,下列命题成立的是______.
- A.A与B均不可逆的充要条件是AB不可逆
- B.r(A)<n与r(B)<n均成立的充要条件是r(AB)<n
- C.Ax=0与Bx=0同解的充要条件是A与B等价
- D.A与B相似的充要条件是E—A与E—B相似
A B C D
D
[考点] 矩阵可逆、同解、相似矩阵的基本结论.
[解析] 通过举反例排除A,B,C项.
解:A项与B项类似,故均错误,而C项仅是必要而非充分条件,故应选D.
事实上,若A~B,则由相似矩阵的性质知E-A~E-B;
反之,若E-A~E-B,则E-(E-A)~E-(E-B),即A~B.
对于选项A,若A与B均不可逆,则|A|=|B|=0,从而|AB|=|A||B|=0,即AB不可逆,但若AB不可逆,推出A与B均不可逆,如A=E,
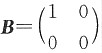
,则AB=B不可逆,但A可逆.
对于选项B,与选项A相近,由于r(AB)≤min{r(A),r(B)},故若r(A)<n与r(B)<n均成立,则r(AB)<n;但反之,若r(AB)<n,推不出r(A)<n或r(B)<n,如A=E,
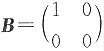
,则r(AB)=r(B)-1<2,但r(A)=2.
对于选项C,由同型矩阵A与B等价
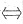
r(A)=r(B)可知,若Ax=0与Bx=0同解,则A与B等价;但反之不然,如
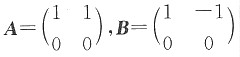
,则A,B等价,但Ax=0与Bx=0显然不同解.
故应选D.
3. 设n维向量α
1,α
2,α
3满足α
1-2α
2+3α
3=0,对任意的n维向量β,向量组α
1+aβ,α
2+bβ,α
3线性相关,则参数a,b应满足条件______
- A.a=b.
- B.a=-b.
- C.a=2b.
- D.a=-2b
A B C D
C
[解析] 法一 因α
1,α
2,α
3满足α
1-2α
2+3α
3=0, (*)
要求向量组α
1+aβ,α
2+bβ,α
3线性相关,其中β是任意向量.利用式(*),取常数k
1=1,k
2=-2,k
3=3,
对向量组α
1+aβ,α
2+bβ,α
3作线性组合,得
(α
1+aβ)-2(α
2+bβ)+3α
3=α
1-2α
2+3α
3+(a-2b)β=(a-2b)β.
故当a=2b时,对任意的n维向量β均有α
1+aβ-2(α
2+bβ)+3α
3=0.
即a=2b时,α
1+aβ,α
2+bβ,α
3对任意β线性相关.故应选C.
法二 α
1+aβ,α
2+bβ,α
3线性相关
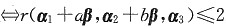
.对矩阵(α
1+aβ,α
2+bβ,α
3)作初等列变换(不改变秩)有
(α
1+aβ,α
2+bβ,α
3)→(α
1+aβ,α
2+bβ,α
1+aβ-2(α
2+bβ)+3α
3)
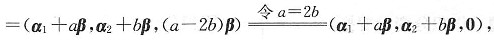
故a=2b时,r(a
1+aβ,α
2+bβ,α
3)≤2,即对任意的n维向量β,有α
1+aβ,α
2+bβ,α
3线性相关,应选C.
4. 设A为m×n矩阵,下列命题中正确的是______
- A.若A中有n阶子式不为零,则Ax=0仅有零解.
- B.若A中有n阶子式不为零,则Ax=b必有唯一解.
- C.若A中有m阶子式不为零,则Ax=0仅有零解.
- D.若A中有,m阶子式不为零,则Ax=b必有唯一解.
A B C D
A
[解析] (A)若A中有n阶子式不为零,此时A为列满秩矩阵,这时n-R(A)=0,则Ax=0仅有零解;反之,若Ax=0仅有零解,则n-R(A)=0.因此,A中有n阶子式不为零是Ax=0仅有零解的充分必要条件.选A.
B.若A中有n阶子式不为零,这时R(A)=n,此时A为列满秩矩阵,这时n-R(A)=0,得不出R(A)=R(A
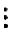
b),得不出Ax=b有解,更得不出Ax=b必有唯一解.B错.
C.若A中有m阶子式不为零,这时R(A)=m,此时A为行满秩矩阵,得不出R(A)=n,得不出Ax=0仅有零解.C错.
D.若A中有m阶子式不为零,此时A为行满秩矩阵,于是有R(A)=R(A
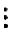
b),这是Ax=b有解的充分必要条件,但得不出Ax=b必有唯一解.D错.
5. 设函数f(x)在x=0处连续,则下列命题错误的是
A.若
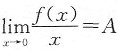
,则f(0)=0.
B.若
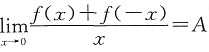
,则f(0)=0.
C.若

,则f'(0)=A.
D.若
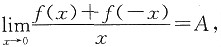
则
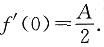
A B C D
D
[解析] 采用举例法.请注意:举的例子必须要满足f(x)在x=0处连续的条件,还要满足
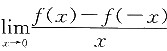
存在的条件.
举例如下:
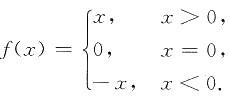
现讨论f(x)在x=0处是否可导,利用可导的定义来讨论.也就是说,计算

由于
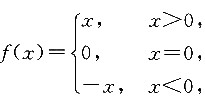
所以
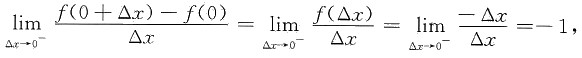
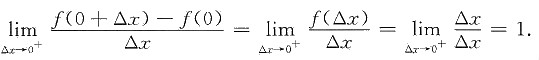
由于
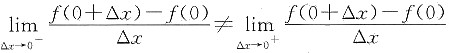
,所以

不存在,从而f(x)在x=0处不可导,所以选项D错误.
6. 设随机变量(X,Y)在区域D={(x,y)|-1≤x≤1,-1≤y≤1}上服从均匀分布,记A
1={X≥0},A
2={Y≥0},A
3={XY≥0},A
4={Y≥X},则下列正确的是______
- A.A1,A2,A3相互独立.
- B.A1,A2,A3两两独立.
- C.A1,A2,A4相互独立.
- D.A1,A2,A4两两独立.
A B C D
B
[解析] 由(X,Y)服从二维均匀分布得到
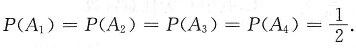
由于
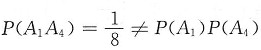
,故A
1,A
4不独立,排除C,D;
由
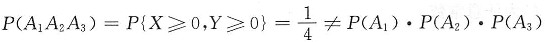
,排除A.
又计算得
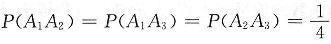
,所以A
1,A
2,A
3两两独立.
7. 对于任意两个事件A和B,______.
A.若
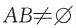
,则A,B一定独立
B.若
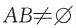
,则A,B有可能独立
C.若
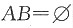
,则A,B一定独立
D.若
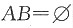
,则A,B一定不独立
A B C D
B
[考点] 考查随机事件的独立性.
[解析] 事件A与B独立的充要条件.
解:由
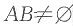
推不出P(AB)=P(A)P(B),因此推不出事件A,B一定独立,排除A项;
若
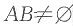
,则P(AB)=0,但P(A)P(B)是否为零不确定,因此C、D项也不成立;
故正确选项为B.
故应选B.
8. 曲线
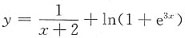
,其渐近线的条数为______
A B C D
D
[解析] 函数
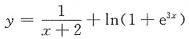
的间断点只有x=-2.
由于
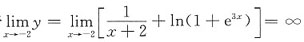
,故x=2为曲线唯一的垂直渐近线.又
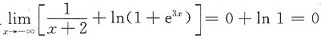
,故x→-∞时,有水平渐近线y=0.
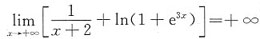
,故x→+∞时没有水平渐近线.但是
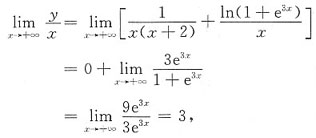
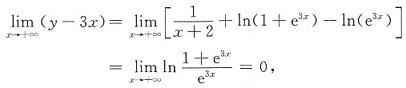
故x→+∞时,有斜渐近线y=3x.
总结:根据间断点求垂直渐近线,根据
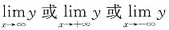
求水平渐近线.注意当自变量x取同一趋向(例x→+∞)时,如果曲线有水平(斜)渐近线,就不可能有斜(水平)渐近线(上面x→+∞也可以是x→-∞或x→∞).但当x取不同趋向时,曲线可以在x→-∞时(或x→+∞时)取到水平渐进线,在x→+∞时(或x→-∞时)取到斜渐近线.
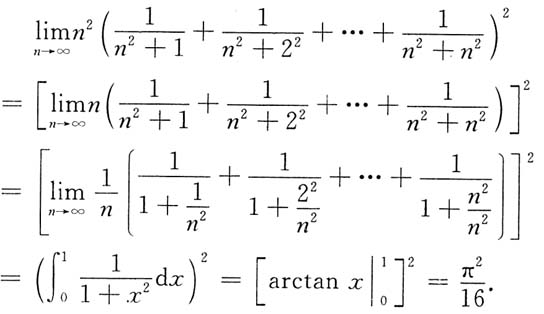
二、填空题1.
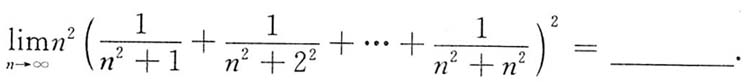
[解析]
2. 设某糖厂的糖果包装机包装好的糖果的重量X服从正态分布,今已知其标准差为σ=0.01(kg).每日开工后在生产线上抽测n袋,得到均值
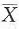
.在显著性水平α=0.05下,要求假设“E(X)=μ=0.5(kg)”的拒绝域为:

或
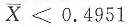
,则n=______.
(注:标准正态分布函数值Φ(1.96)=0.975,Φ(1.645)=0.95)
16
[解析] X~N(μ,σ
2),其中σ=0.01,μ=0.5,则
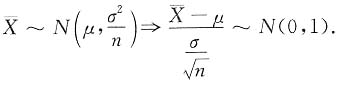
又σ=0.01,μ=0.5,故
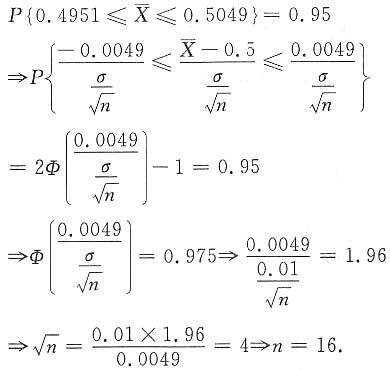
3. 设空间区域
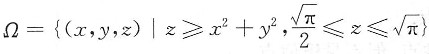
,则
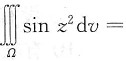
______.
[解析] 用柱面坐标,

于是
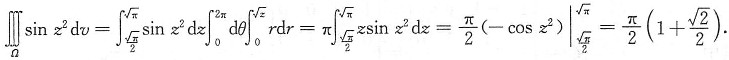
4. 设f(x)是连续函数,则
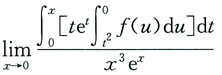
=______.
0
[解析]
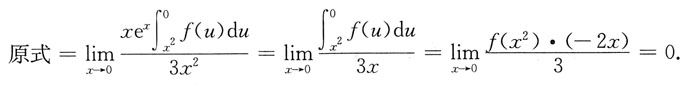
5.
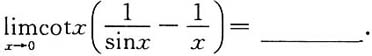
6.
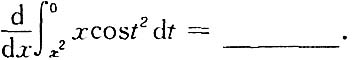
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.下求下列定积分.1.

解:
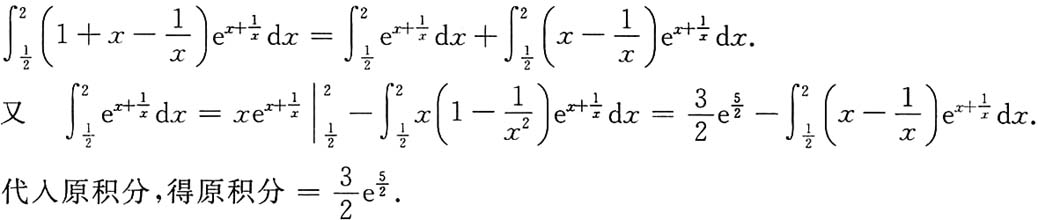
2.
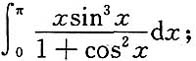
3.
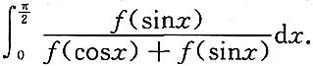
4. 求曲线y=ln(1-x
2)上相应于
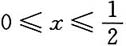
的一段弧.
解:
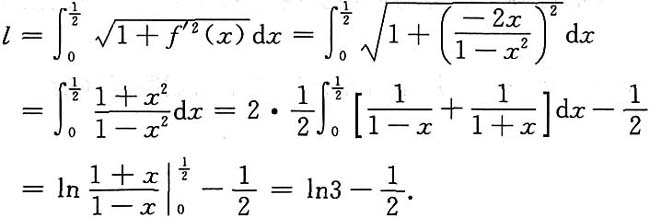
5. (3x
2+2xe
-y)dx+(3y
2-x
2e
-y)dy=0;
解:因为
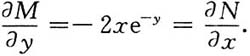
所以方程为全微分方程,于是有
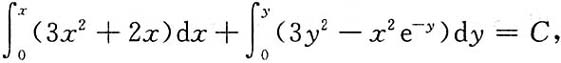
即x
3+x
2+y
3+x
2e
-y-x
2=C,亦即
原方程的通解为x
3+y
3+x
2e
-y=C.
6.
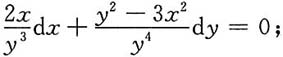
解:因为
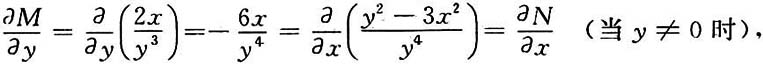
所以方程为全微分方程.于是有
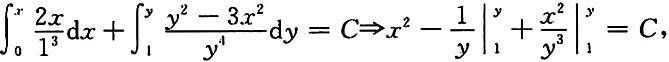
故原方程的解为
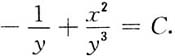
7. 2xy
3dx+(x
2y
2-1)dy=0.
解:因为
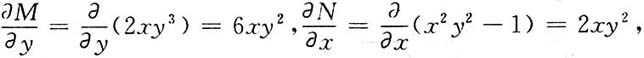
所以方程不是全微分方程.
方程可改写成(2xy
3dx+x
2y
2dy)-dy=0,
用简单的观察法看出积分因子为
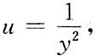
于是,

8. 求摆线

上相应于0≤t≤2π的一拱.
解:
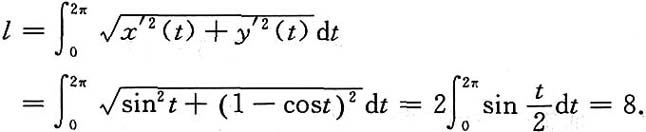
9. 球面
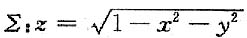
上侧,a,b,c为任意常数,求曲面积分
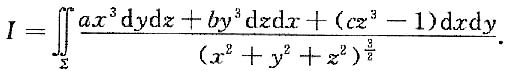
解:方法1
由于是在球面上积分,

其中,
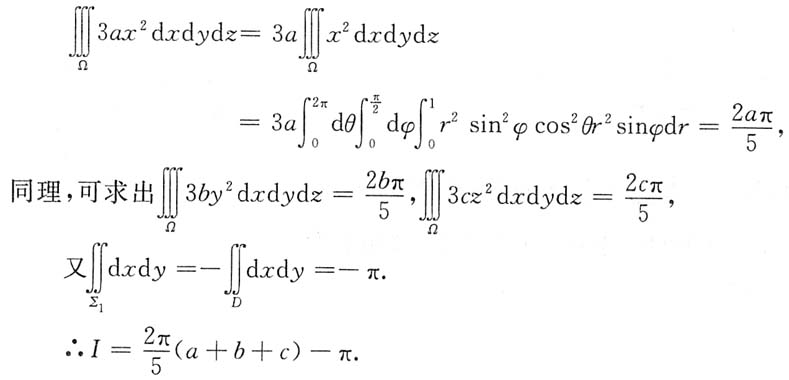
方法2
曲面:F(x,y,z)=x
2+y
2+z
2-1=0,
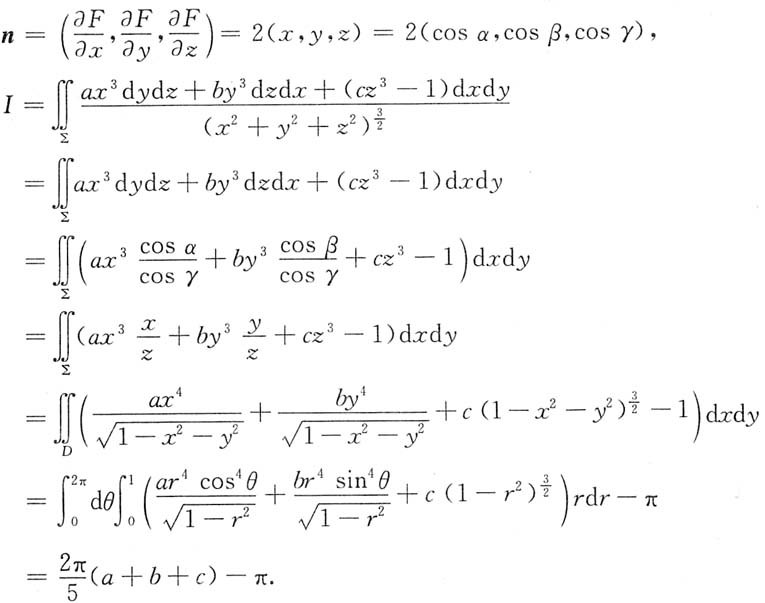
10. 设f(x)在[1,+∞)上有连续的二阶导数,f(1)=0,f'(1)=1,且二元函数z=(x
2+y
2)f(x
2+y
2)满足
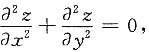
求f(x)在[1,+∞)的最大值.
解:
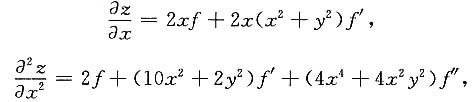
根据对称性得
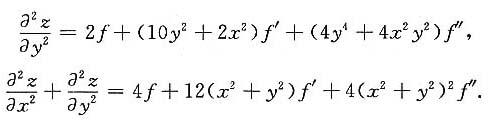
令x
2+y
2=r,由
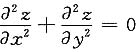
得f+3rf'+r
2f''=0,
令r=e
t,
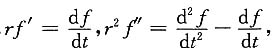
整理得
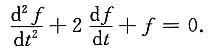
解得f=(C
1+C
2t)e
-t,于是
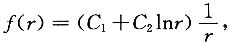
由f(1)=0,得C
1=0,
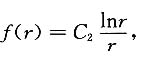
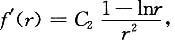
由f'(1)=1,得C
2=1,于是
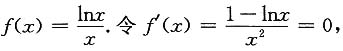
得x=e,当x∈(1,e)时,f’(x)>0,当x>e时,f’(x)<0,则x=e为f(x)在[1,+∞)上的最大值点,最大值为
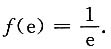
11. 设函数f(x)和g(x)在区间[a,b]上连续,在区间(a,b)内可导,且f(a)=g(b)=0,g'(x)<0.试证明存在ξ∈(a,b)使
证明:令
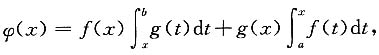
显然函数φ(x)在区间[a,b]上连续,函数φ(x)在区间(a,b)内可导,且
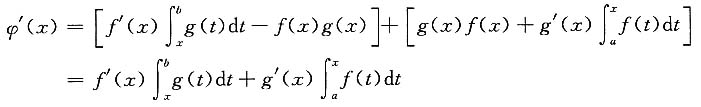
另外,又有φ(a)=φ(b)=0.
所以根据罗尔定理可知存在ξ∈(a,b)使φ'(ξ)=0,即
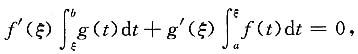
由于g(b)=0及g'(x)<0,所以区间(a,b)内必有g(x)>0,从而就有
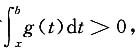
于是有
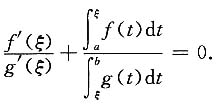
12. 设z=z(x,y)是由x
2-6xy+10y
2-2yz-z
2+18=0确定的函数,求z=z(x,y)的极值点和极值.
解:可能极值点是两个一阶偏导数为零的点,先求出一阶偏导,再令其为零确定极值点即可,然后用二阶偏导确定是极大值还是极小值,并求出相应的极值.
因为x
2-6xy+10y
2-2yz-z
2+18=0,所以
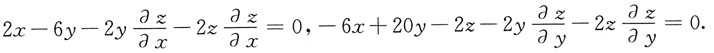
令
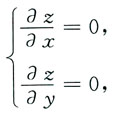
得
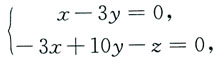
故
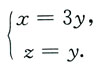
将上式代入x
2-6xy+10y
2-2yz-z
2+18=0,可得

由于
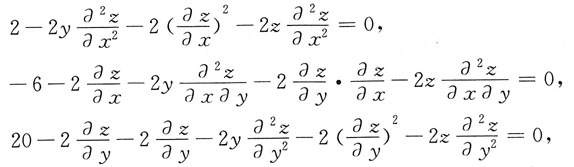
所以
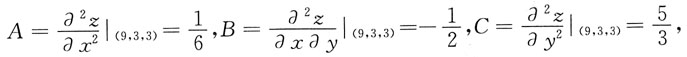
故
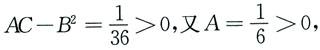
从而点(9,3)是z(x,y)的极小值点,极小值为z(9,3)=3.
类似地,由
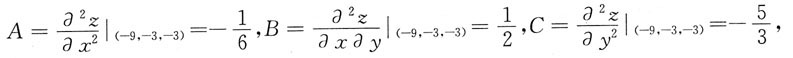
可知
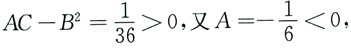
从而点(-9,-3)是z(x,y)的极大值点,极大值.
[解析] 本题讨论由方程所确定的隐函数求极值问题,关键是求可能极值点时应注意x,y,z满足原方程.
13. 证明:当a,b,c不共面时,方程组
xa+yb+zc=d ①
有以下解:
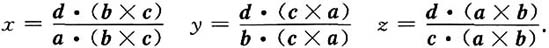
证明:将式①的两边点乘b×c,并注意到:b,b,c共面,c,b,c共面,则有
(xa+yb+zc)·(b×c)=xa·(b×c)+yb·(b×c)+zc·(b×c)
=xa·(b×c).
即xa·(b×c)=d·(b×c),
故,
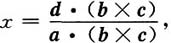
同理可证y与z的表达式成立.
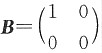 ,则AB=B不可逆,但A可逆.
,则AB=B不可逆,但A可逆.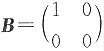 ,则r(AB)=r(B)-1<2,但r(A)=2.
,则r(AB)=r(B)-1<2,但r(A)=2.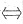 r(A)=r(B)可知,若Ax=0与Bx=0同解,则A与B等价;但反之不然,如
r(A)=r(B)可知,若Ax=0与Bx=0同解,则A与B等价;但反之不然,如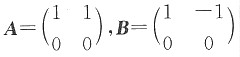 ,则A,B等价,但Ax=0与Bx=0显然不同解.
,则A,B等价,但Ax=0与Bx=0显然不同解.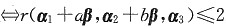 .对矩阵(α1+aβ,α2+bβ,α3)作初等列变换(不改变秩)有
.对矩阵(α1+aβ,α2+bβ,α3)作初等列变换(不改变秩)有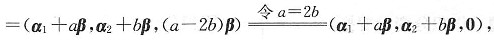
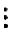 b),得不出Ax=b有解,更得不出Ax=b必有唯一解.B错.
b),得不出Ax=b有解,更得不出Ax=b必有唯一解.B错.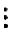 b),这是Ax=b有解的充分必要条件,但得不出Ax=b必有唯一解.D错.
b),这是Ax=b有解的充分必要条件,但得不出Ax=b必有唯一解.D错.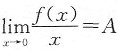 ,则f(0)=0.
,则f(0)=0.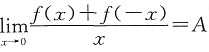 ,则f(0)=0.
,则f(0)=0. ,则f'(0)=A.
,则f'(0)=A.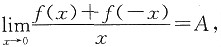 则
则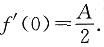
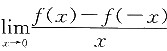 存在的条件.
存在的条件.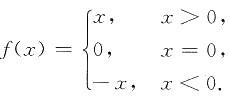

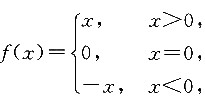 所以
所以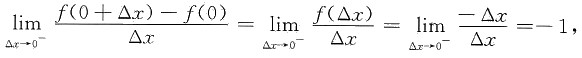
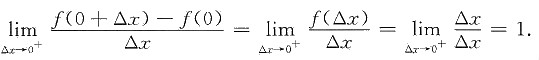
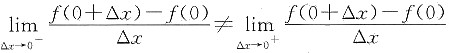 ,所以
,所以 不存在,从而f(x)在x=0处不可导,所以选项D错误.
不存在,从而f(x)在x=0处不可导,所以选项D错误.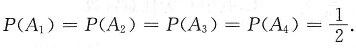
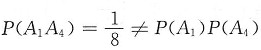 ,故A1,A4不独立,排除C,D;
,故A1,A4不独立,排除C,D;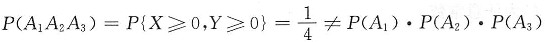 ,排除A.
,排除A.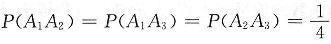 ,所以A1,A2,A3两两独立.
,所以A1,A2,A3两两独立.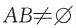 ,则A,B一定独立
,则A,B一定独立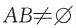 ,则A,B有可能独立
,则A,B有可能独立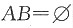 ,则A,B一定独立
,则A,B一定独立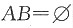 ,则A,B一定不独立
,则A,B一定不独立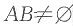 推不出P(AB)=P(A)P(B),因此推不出事件A,B一定独立,排除A项;
推不出P(AB)=P(A)P(B),因此推不出事件A,B一定独立,排除A项;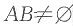 ,则P(AB)=0,但P(A)P(B)是否为零不确定,因此C、D项也不成立;
,则P(AB)=0,但P(A)P(B)是否为零不确定,因此C、D项也不成立;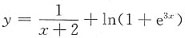 ,其渐近线的条数为______
,其渐近线的条数为______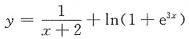 的间断点只有x=-2.
的间断点只有x=-2.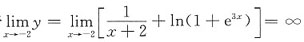 ,故x=2为曲线唯一的垂直渐近线.又
,故x=2为曲线唯一的垂直渐近线.又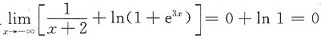 ,故x→-∞时,有水平渐近线y=0.
,故x→-∞时,有水平渐近线y=0.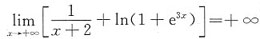 ,故x→+∞时没有水平渐近线.但是
,故x→+∞时没有水平渐近线.但是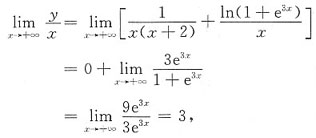
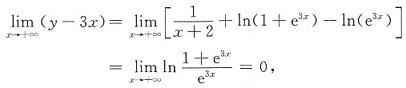
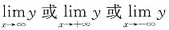 求水平渐近线.注意当自变量x取同一趋向(例x→+∞)时,如果曲线有水平(斜)渐近线,就不可能有斜(水平)渐近线(上面x→+∞也可以是x→-∞或x→∞).但当x取不同趋向时,曲线可以在x→-∞时(或x→+∞时)取到水平渐进线,在x→+∞时(或x→-∞时)取到斜渐近线.
求水平渐近线.注意当自变量x取同一趋向(例x→+∞)时,如果曲线有水平(斜)渐近线,就不可能有斜(水平)渐近线(上面x→+∞也可以是x→-∞或x→∞).但当x取不同趋向时,曲线可以在x→-∞时(或x→+∞时)取到水平渐进线,在x→+∞时(或x→-∞时)取到斜渐近线.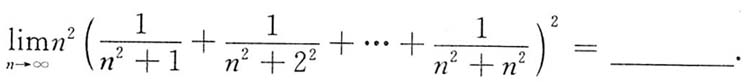


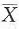 .在显著性水平α=0.05下,要求假设“E(X)=μ=0.5(kg)”的拒绝域为:
.在显著性水平α=0.05下,要求假设“E(X)=μ=0.5(kg)”的拒绝域为: 或
或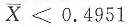 ,则n=______.
,则n=______.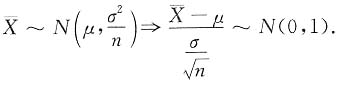
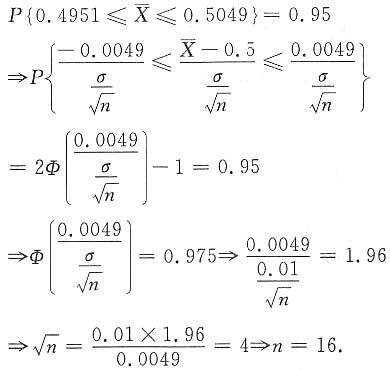
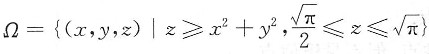 ,则
,则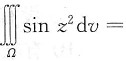 ______.
______.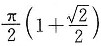
 于是
于是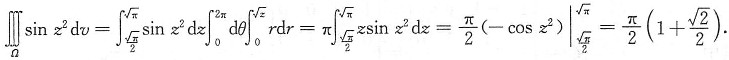
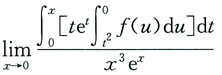 =______.
=______.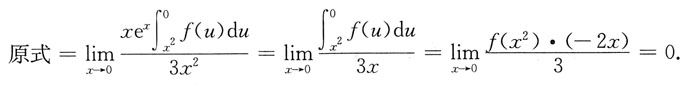
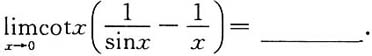
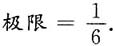
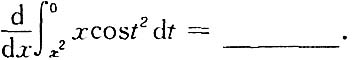
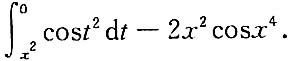

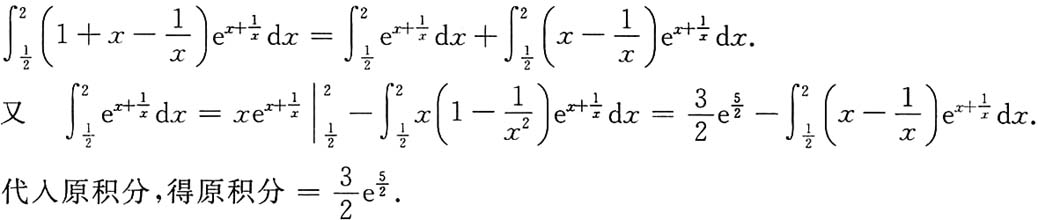
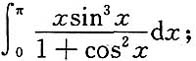
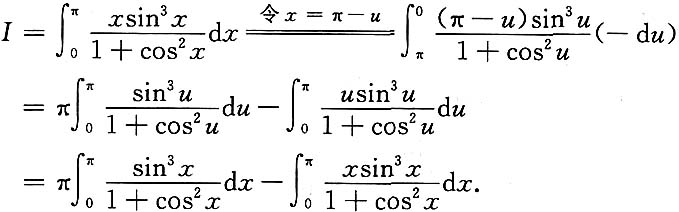
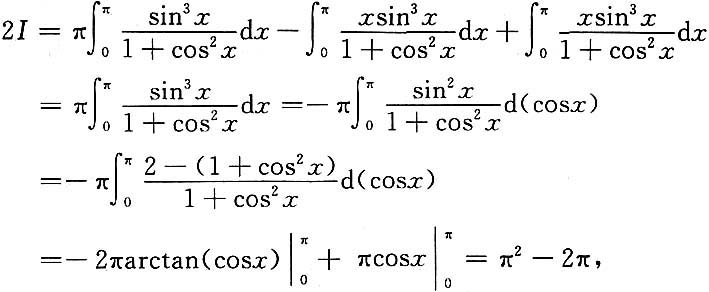
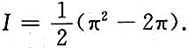
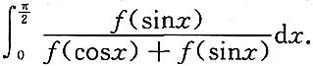
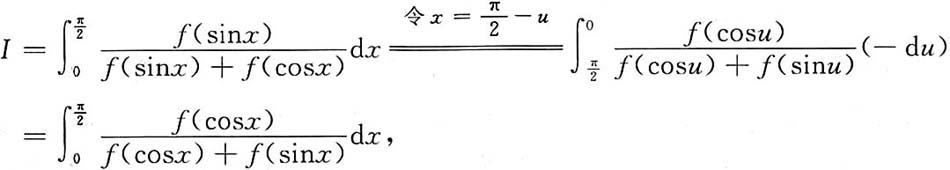
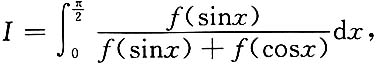
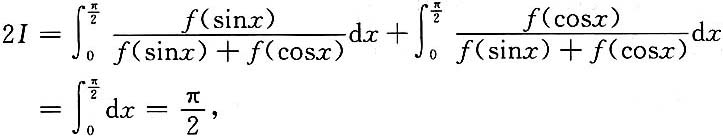
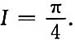
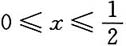 的一段弧.
的一段弧.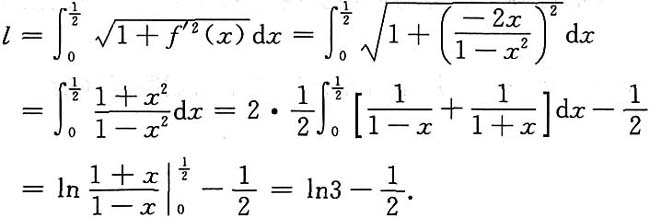
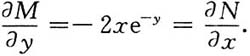
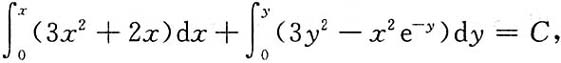
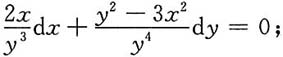
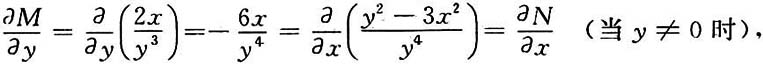
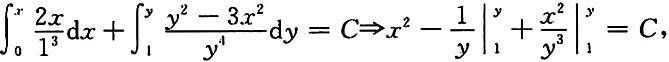
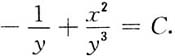
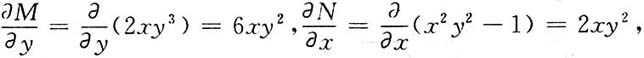
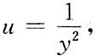

 上相应于0≤t≤2π的一拱.
上相应于0≤t≤2π的一拱.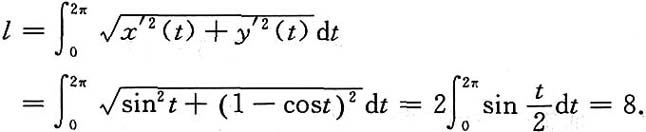
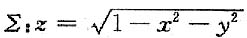 上侧,a,b,c为任意常数,求曲面积分
上侧,a,b,c为任意常数,求曲面积分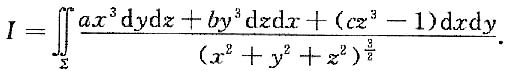

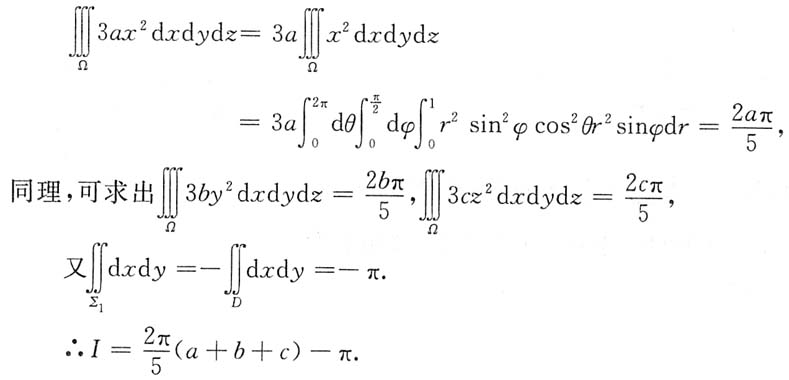
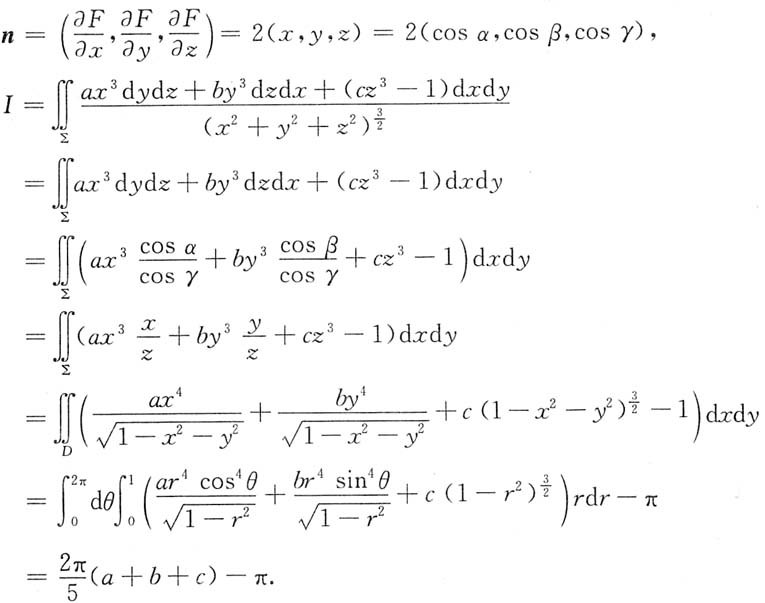
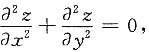 求f(x)在[1,+∞)的最大值.
求f(x)在[1,+∞)的最大值.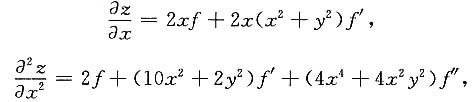
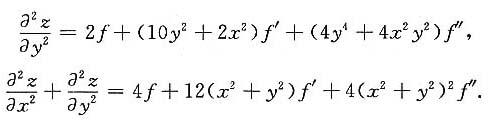
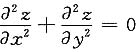 得f+3rf'+r2f''=0,
得f+3rf'+r2f''=0,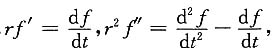 整理得
整理得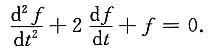
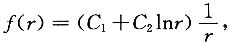 由f(1)=0,得C1=0,
由f(1)=0,得C1=0,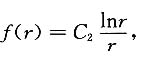
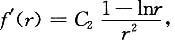 由f'(1)=1,得C2=1,于是
由f'(1)=1,得C2=1,于是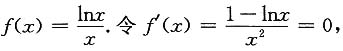 得x=e,当x∈(1,e)时,f’(x)>0,当x>e时,f’(x)<0,则x=e为f(x)在[1,+∞)上的最大值点,最大值为
得x=e,当x∈(1,e)时,f’(x)>0,当x>e时,f’(x)<0,则x=e为f(x)在[1,+∞)上的最大值点,最大值为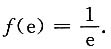
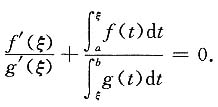
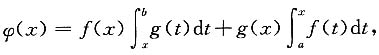 显然函数φ(x)在区间[a,b]上连续,函数φ(x)在区间(a,b)内可导,且
显然函数φ(x)在区间[a,b]上连续,函数φ(x)在区间(a,b)内可导,且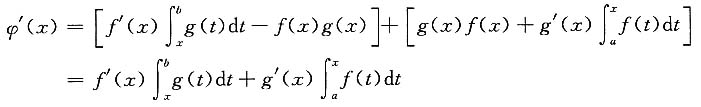
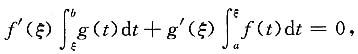
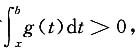 于是有
于是有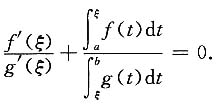
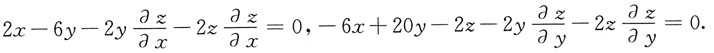
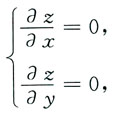 得
得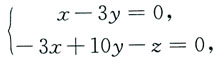
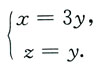

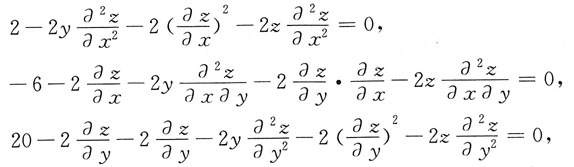
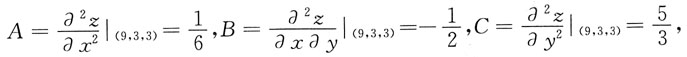
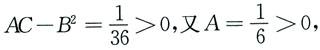 从而点(9,3)是z(x,y)的极小值点,极小值为z(9,3)=3.
从而点(9,3)是z(x,y)的极小值点,极小值为z(9,3)=3.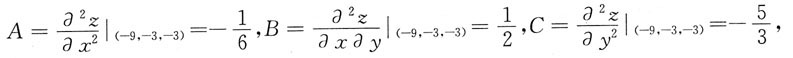
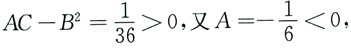 从而点(-9,-3)是z(x,y)的极大值点,极大值.
从而点(-9,-3)是z(x,y)的极大值点,极大值.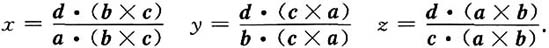
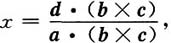 同理可证y与z的表达式成立.
同理可证y与z的表达式成立.