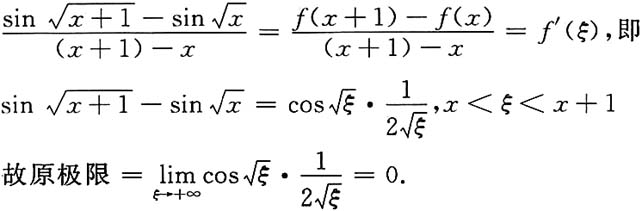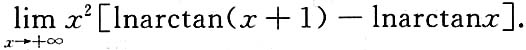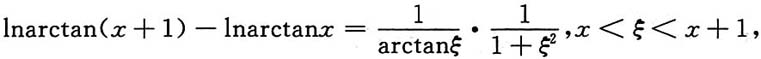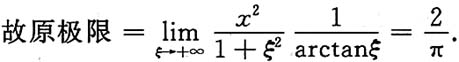银符考试题库B12
现在是:
试卷总分:150.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
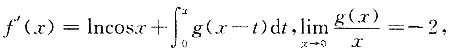 则______.
则______.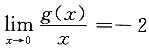 得g(0)=0,g'(0)=-2.
得g(0)=0,g'(0)=-2.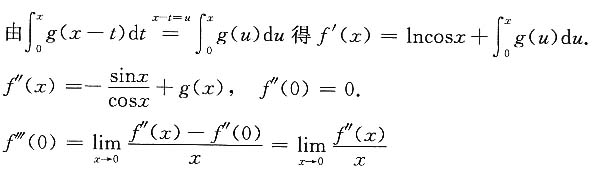
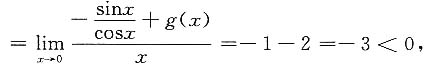
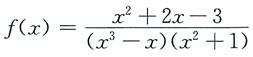 垂直渐近线的个数为______
垂直渐近线的个数为______ 条件收敛,则它的收敛半径R=1;
条件收敛,则它的收敛半径R=1;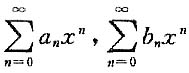 的收敛半径分别为R1,R2,则
的收敛半径分别为R1,R2,则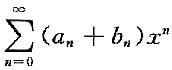 的收敛半径R=min(R1,R2);
的收敛半径R=min(R1,R2);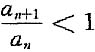 ,(n=1,2,…),则
,(n=1,2,…),则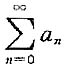 收敛.
收敛.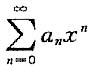 绝对收敛,因而
绝对收敛,因而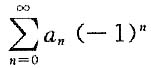 绝对收敛,与已知矛盾;
绝对收敛,与已知矛盾;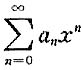 发散,这也与已知矛盾.因此,R=1.
发散,这也与已知矛盾.因此,R=1.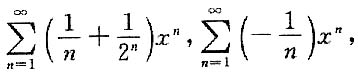
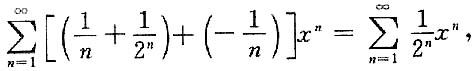
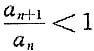 推不出
推不出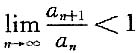 ,因而得不出正项级数
,因而得不出正项级数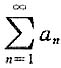 收敛,例如调和级数
收敛,例如调和级数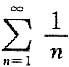 就是这样.③不正确.选B.
就是这样.③不正确.选B.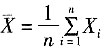 ,则下列结论中不正确的是______
,则下列结论中不正确的是______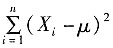 服从χ2分布
服从χ2分布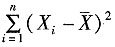 服从χ2分布
服从χ2分布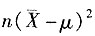 服从χ2分布
服从χ2分布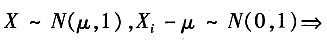
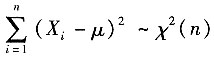 ,A正确
,A正确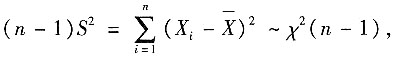 C正确,
C正确, D正确,
D正确,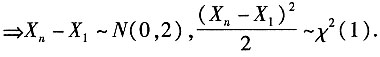
 ,则______
,则______
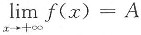 ,A为正数.
,A为正数.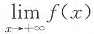 可能存在,也可能不存在.
可能存在,也可能不存在.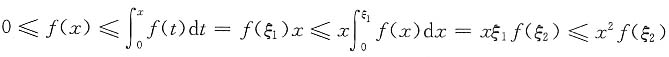 ,0<ξ1,ξ2<x.做类似推导下去,可得
,0<ξ1,ξ2<x.做类似推导下去,可得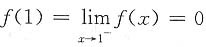 ,
, .
. 为______
为______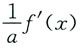
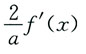
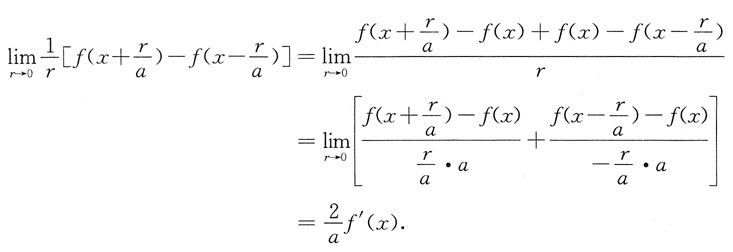
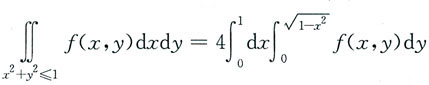 成立的充分条件是______
成立的充分条件是______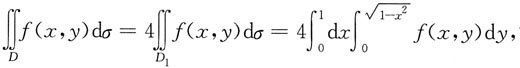 故选D.
故选D.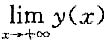 ______
______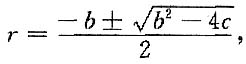
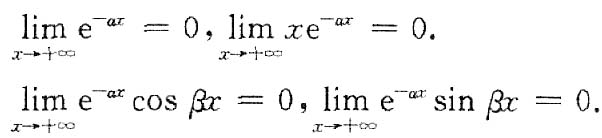
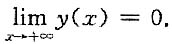
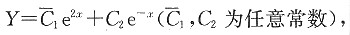
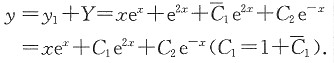
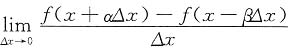 =______.
=______.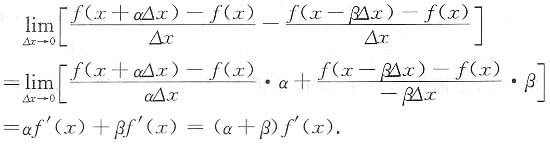
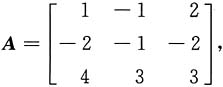 则A-1=______,(A*)-1=______,[(-2A)*]-1=______.
则A-1=______,(A*)-1=______,[(-2A)*]-1=______.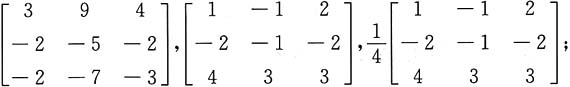
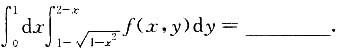
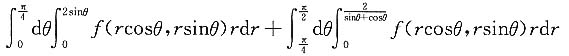
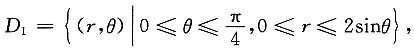
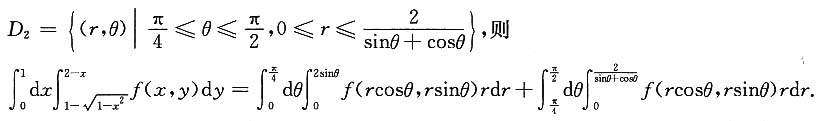
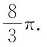
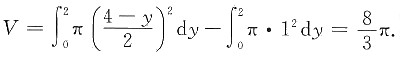
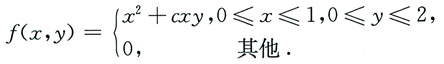

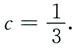
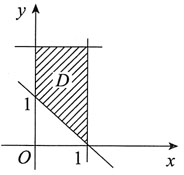

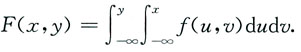
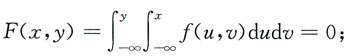
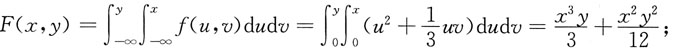
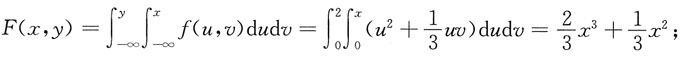
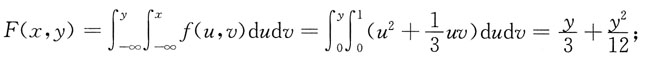
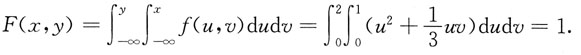
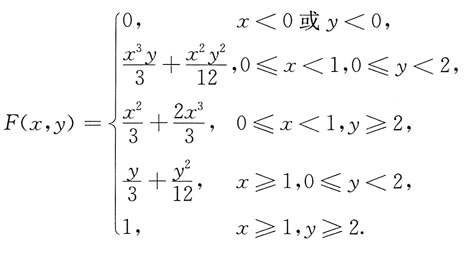
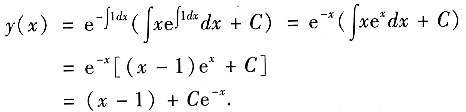
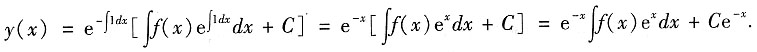
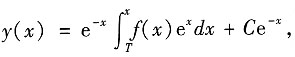 则有
则有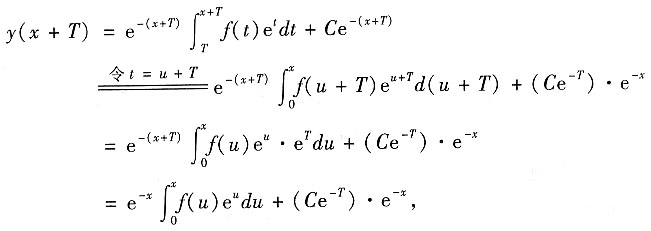
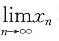 存在并求此极限.
存在并求此极限.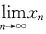 存在,先证{xn}单调增加,由
存在,先证{xn}单调增加,由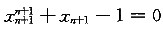 与
与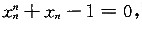
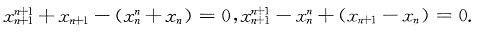
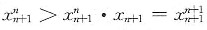 ,于是有
,于是有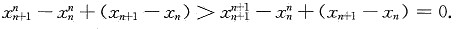
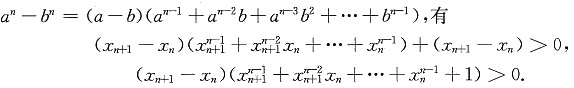
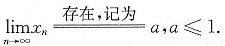
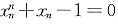 ,有
,有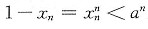 .令n→∞,得
.令n→∞,得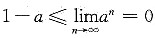 ,得a≥1,矛盾.所以a=1,即
,得a≥1,矛盾.所以a=1,即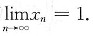 证毕.
证毕.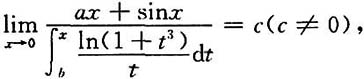 试确定a,b,c的值.
试确定a,b,c的值.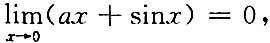
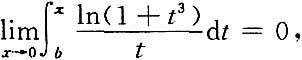 而当x→0时,
而当x→0时,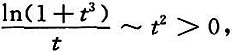 所以b=0.
所以b=0.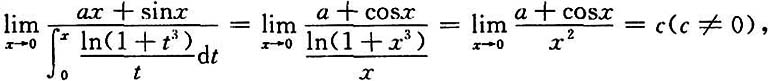 而
而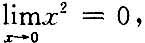
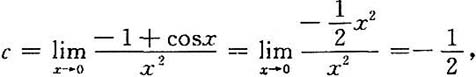
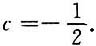
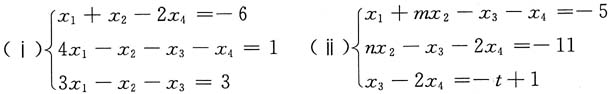
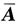 作初等行变换
作初等行变换
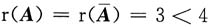 ,所以方程组(ⅰ)有无穷多解,得其导出组的基础解系为[1,1,2,1]T,非齐次方程的一个特解是[-2,-4,-5,0]T,故方程组(ⅰ)的通解为
,所以方程组(ⅰ)有无穷多解,得其导出组的基础解系为[1,1,2,1]T,非齐次方程的一个特解是[-2,-4,-5,0]T,故方程组(ⅰ)的通解为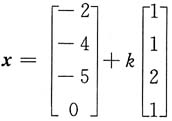 ,k为任意常数,
,k为任意常数,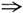 m=2,n=4,t=6.又当m=2,n=4,t=6时,(ⅱ)的系数矩阵的秩和增广矩阵的秩均为3.则(ⅱ)的解也是(ⅰ)的解.因此当m=2,n=4,t=6时,方程组(ⅰ)与(ⅱ)同解.
m=2,n=4,t=6.又当m=2,n=4,t=6时,(ⅱ)的系数矩阵的秩和增广矩阵的秩均为3.则(ⅱ)的解也是(ⅰ)的解.因此当m=2,n=4,t=6时,方程组(ⅰ)与(ⅱ)同解.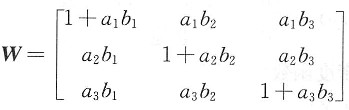 ,其中a1b1+a2b2+a3b3=0.
,其中a1b1+a2b2+a3b3=0.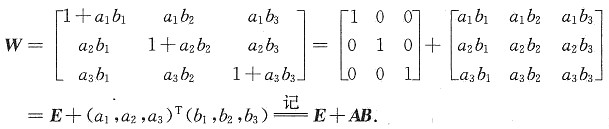
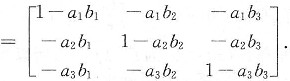
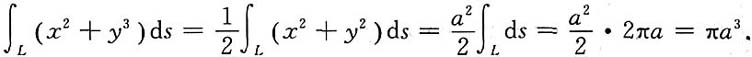
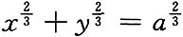 所围成的图形绕x轴旋转所得旋转体体积.
所围成的图形绕x轴旋转所得旋转体体积.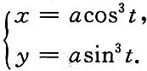
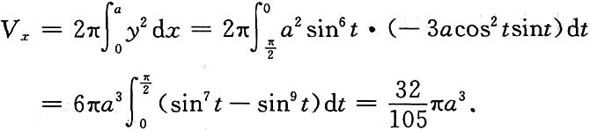
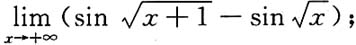
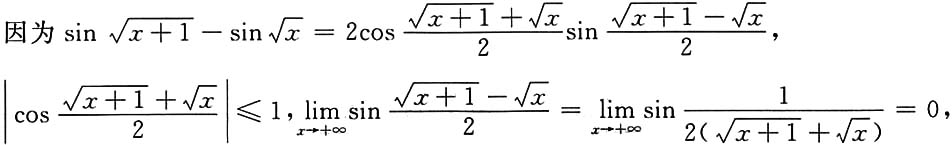
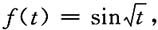 显然当x>0时,f(t)在[x,x+1]上满足拉格朗日中值定理,于是有
显然当x>0时,f(t)在[x,x+1]上满足拉格朗日中值定理,于是有