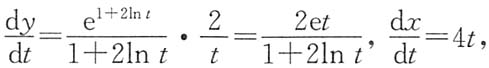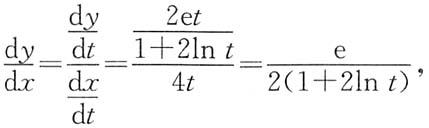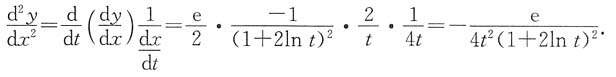一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.2. 设有以下结论:

则以上结论中正确的是
A B C D
D
[解析] 先看结论②,
结论②说的是定积分
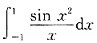
(注意:很多同学认为
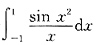
是反常积分,其实不然,因为

存在)等于0.
现在来验证一下.
请看如下定理:
设
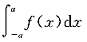
是一个定积分,如果f(x)在区间[-a,a]上连续且,f(x)在区间[-a,a]上是一个奇函数,则定积分
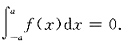
有同学认为
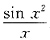
虽为奇函数,但在区间[-1,1]上并不连续,因此不能使用上述定理,的确,
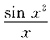
在区间[-1,1]上并不连续,但由于定积分的被积函数在某一点处的函数值是完全无所谓的,所以可以把结论②中所说的“
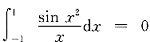
”改写为“
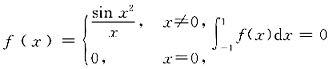
”.这样一来,f(x)在区间[-1,1]上连续,且为奇函数,根据以上定理可知,结论②正确.
再看结论③.
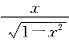
在x=1,x=-1处没有定义.现在算一下
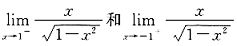
,这两个极限只要有一个是∞,就说明
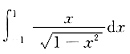
是反常积分.通过计算可知

和
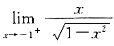
这两个极限都是∞,所以
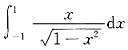
是反常积分,而不是定积分.
结论③说的是反常积分
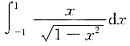
等于0.
请看以下定理:
设
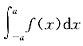
是一个反常积分,如果f(x)在除x=±c外的区间[-a,a]上连续(其中c为[-a,a]上的点),且f(x)在除±c外的区间[-a,a]上是一个奇函数,且
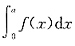
的值是一个常数,则反常积分
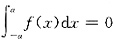
.
根据以上定理来验证一下.
首先,
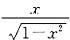
在区间[-1,1]上除了x=±1连续(也就是说
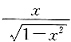
在区间(-1,1)上连续),这是毫无疑问的,
其次,说
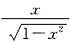
在区间(-1,1)上是一个奇函数也对.
最后,看
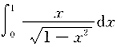
是否等于一个常数.通过计算可知答案是常数,所以结论③正确.
3. 设f(x)二阶连续可导,且
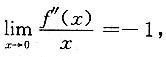
则______.
- A.f(0)是f(x)的极小值
- B.f(0)是f(x)的极大值
- C.(0,f(0))是曲线y=f(x)的拐点
- D.x=0是f(x)的驻点但不是极值点
A B C D
C
[解析] 因为f(x)二阶连续可导,且
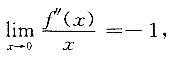
所以
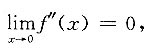
即f"(0)=0.又
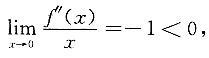
由极限的保号性,存在δ>0,当0<|x|<δ时,有
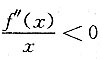
,即当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,所以(0,f(0))为曲线y=f(x)的拐点,选C.
4. 设A是m×s矩阵,B是s×n矩阵,则线性方程组ABx=0和Bx=0是同解方程组的一个充分条件是______
- A.r(B)=n.
- B.r(B)=s.
- C.r(A)=s.
- D.r(A)=m.
A B C D
C
[解析] 若x
0≠0,使得Bx
0=0.两边左乘A,得ABx
0=0;反之,若x
0≠0,使得ABx
0=0,且r(A)=s(A的列向量线性无关),则由
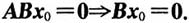
故,r(A)=s
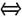
Bx=0和ABx=0是同解方程组.故应选C.
5. 设A,B均为2阶方阵,A
*,B
*分别为A,B的伴随矩阵.若|A|=2,|B|=3,则分块矩阵
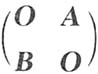
的伴随矩阵为
A.
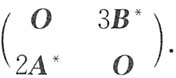
B.

C.
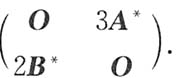
D.

A B C D
B
[解析] 解法1 对任一n阶矩阵C,有
C
*C=CC
*=|C|E,
其中C
*是C的伴随矩阵.因此可直接用乘法验证,排除错误选项.
对选项A,有
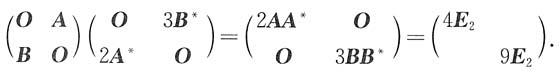
E
2为2阶单位矩阵;
对选项B,有

E
4为4阶单位矩阵;
对选项C,D,分别有
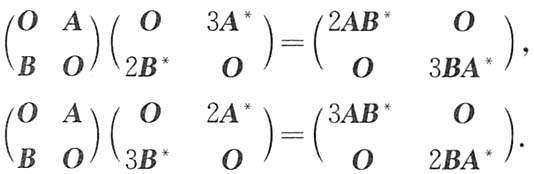
由此知选项B正确.
解法2 设
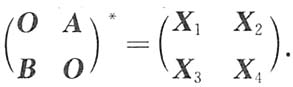
分别求出X
1,X
2,X
3,X
4.因为
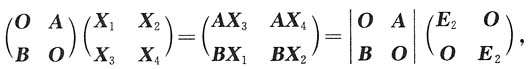
所以BX
1=O,AX
4=O,由已知,A,B均可逆,故X
1=x
4=O;另一方面,有
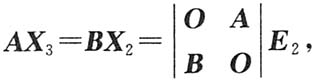
其中
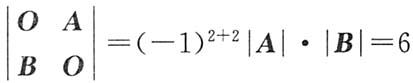
,故得
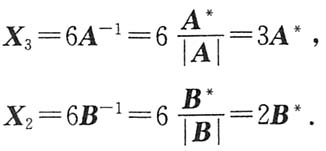
解法3
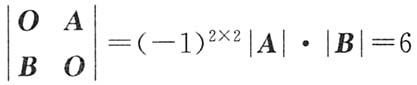
,则
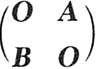
可逆,于是

选B.
6. 设
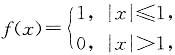
则f{f[f(x)]}=
A.0.
B.1.
C.

D.
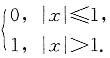
A B C D
B
[解析] 由于f(x)≤1,故f[f(x)]=1,因而
f{f[f(x)]}=1.
8. 设A是三阶矩阵,其中a
11≠0,A
ij=a
ij,i=1,2,3,j=1,2,3,则|2A
T|=
A B C D
D
[解析]
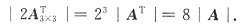

故A*=A
T AA*=AAT=|A|E,两边取行列式,得
|AA
T|=|A|
2=|A|E|=|A|
3 得|A|
2(|A|-1)=0
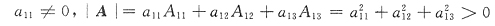
故|A|=1,从而|2A
T|=8.
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.1. 设
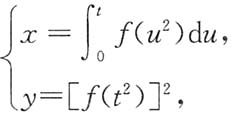
其中f(u)具有二阶导数,且f(u)≠0,求
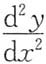
.
解:因为
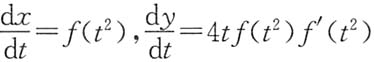
,所以
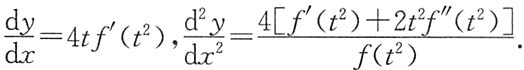
2. 设y=y(x)由x
2y
2+y=1(y>0)确定,求函数y=y(x)的极值.
解:x
2y
2+y=1两边关于x求导得
2xy
2+2x
2yy'+y'=0,解得
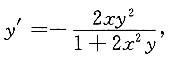
由
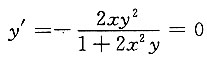
得x=0,
2xy
2+2x
2yy'+y'=0两边对x求导得
2y
2+8xyy'+2x
2y'
2+2x
2yy"+y"=0,
将x=0,y=1,y'(0)=0代入得y"(0)=-2<0,
故x=0为函数y=y(x)的极大点,极大值为y(0)=1.
3. 计算
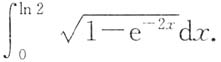
解:解法1 原式
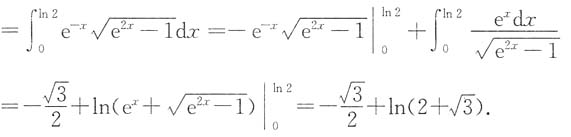
解法2 令e
-x=sint,则
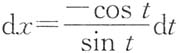
,
原式=
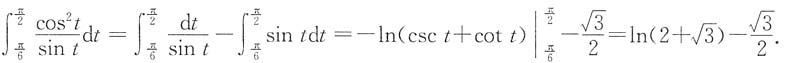
4. 设f(x)在(-∞,+∞)有定义,f(x+y)=f(x)+f(y)+2xy,f'(0)=a,求f(x).
解:令x=0,y=0得f(0)=0.
由
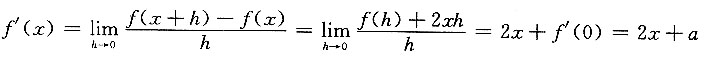
得
f(x)=x
2+ax+C,
由f(0)=0得C=0,故f(x)=x
2+ax.
5. 求不定积分
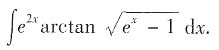
解:

提示:本题还可利用变量替换求解.令
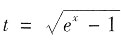
,化简过后,利用分部积分逐步求解.最后求得关于t的表达式后,记得将
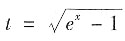
再代回去.(求解过程略)
6. 设f(x),f(x)在x=x
0都是可导的,又F(x)=f(x)|g(x)|.求证:
(Ⅰ)若g(x
0)≠0,则F(x)在x=x
0处可导;
(Ⅱ)若g(x
0)=0,则F(x)在x=x
0处可导的充要条件是f(x
0)=0或g'(x
0)=0.这时必有F'(x
0)=0.
证明:g(x)连续
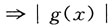
连续.但g(x)可导
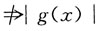
可导.当|g(x)|可导,由可导性运算法则知F(x)可导,当|g(x)|不可导(或不知是否可导时),则按定义考察F(x)的可导性.
(Ⅰ)若
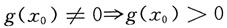
(或g(x
0)<0),由g(x)在x=x
0连续

当x∈(x
0-δ,x
0+δ)时g(x)>0(或g(x)<0),
于是
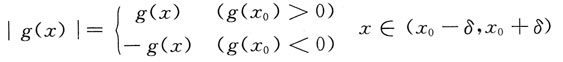
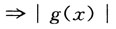
与g(x)在x=x
0有相同的可导性,即|g(x)|在x=x
0可导,
从而F(x)=f(x)|g(x)|在x=x
0可导.
(Ⅱ)若g(x
0)=0.按定义考察F(x)在x=x
0的可导性.
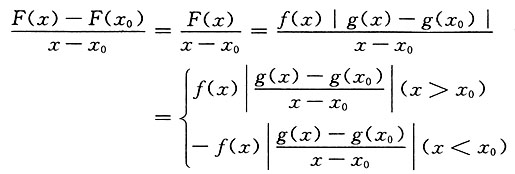
于是要分别考察
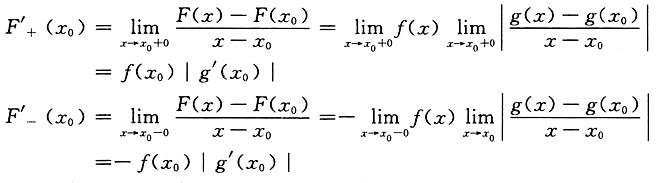
因此
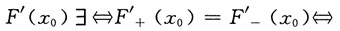
f(x
0)|g'(x
0)|=-f(x
0)|g'(x
0)|
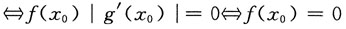
或g'(x
0)=0.
此时F'(x
0)=F'
+(x
0)=F'
-(x
0)=0.
7. 讨论曲线y=4lnx+k与y=4x+ln
4x的交点个数.
解:解法1 问题等价于讨论方程ln
4x-4lnx+4x-k=0有几个不同的实根。
设φ(x)=ln
4x-4lnx+4x-k,
则有
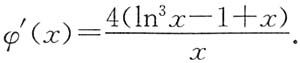
不难看出,x=1是φ(x)的驻点.
当0<x<1时,φ'(x)<0,即φ(x)单调减少;当x>1时,φ'(x)>0,即φ(x)单调增加,故φ(1)=4-k为函数φ(x)的最小值.
当k<4,即4-k>0时,φ(x)=0无实根,即两条曲线无交点;
当k=4,即4-k=0时,φ(x)=0有唯一实根,即两条曲线只有一个交点;
当k>4,即4-k<0时,由于
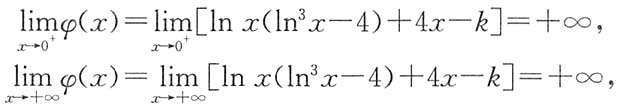
故φ(x)=0有两个实根,分别位于(0,1)与(1,+∞)内,即两条曲线有两个交点.
解法2 问题等价于讨论方程k=4x-4lnx+ln
4x的不同实根的个数.
设f(x)=4x-4lnx+ln
4x,则
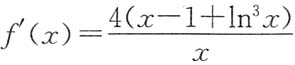
,不难看出x=1是f(x)的驻点.又f"(x)=
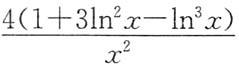
,f"(x)>0,所以f(1)=4为f(x)的最小值.
当k<4时,方程f(x)=k无实根,即两曲线无交点;
当k=4时,方程f(x)=k有唯一实根,即两曲线只有一个交点;
当k>4时,由于
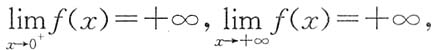
所以方程f(x)=k有两个实根分别位于区间(0,1)与(1,+∞)内,即两曲线有两个交点.
8. 若g(x)在x=c处二阶导数存在,且g'(c)=0,g"(c)<0,则g(c)为g(x)的一个极大值.
证明:因
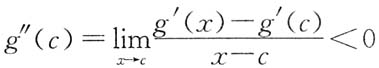
,而g'(c)=0,故
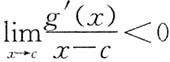
.由极限的保号性,
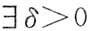
,当x∈(c-δ,c)时,有
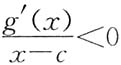
,即g'(x)>0,从而g(x)在(c-δ,c)上单增;当x∈(c,c+δ)时,有
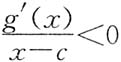
,即g'(x)<0,从而g(x)在(c-δ,c)上单减.
又由g'(c)=0知,x=c是g(x)的驻点,因此g(c)为g(x)的一个极大值.
9. 设函数y=y(x)由参数方程
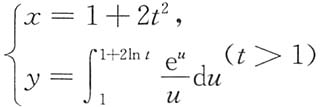
所确定,求

解:由
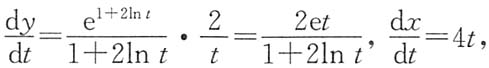
得
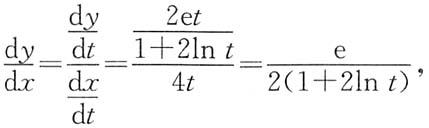
所以
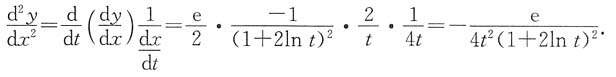
当x=9时,由x=1+2t
2及t>1得t=2,故


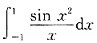 (注意:很多同学认为
(注意:很多同学认为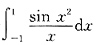 是反常积分,其实不然,因为
是反常积分,其实不然,因为 存在)等于0.
存在)等于0.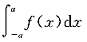 是一个定积分,如果f(x)在区间[-a,a]上连续且,f(x)在区间[-a,a]上是一个奇函数,则定积分
是一个定积分,如果f(x)在区间[-a,a]上连续且,f(x)在区间[-a,a]上是一个奇函数,则定积分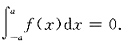
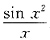 虽为奇函数,但在区间[-1,1]上并不连续,因此不能使用上述定理,的确,
虽为奇函数,但在区间[-1,1]上并不连续,因此不能使用上述定理,的确,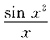 在区间[-1,1]上并不连续,但由于定积分的被积函数在某一点处的函数值是完全无所谓的,所以可以把结论②中所说的“
在区间[-1,1]上并不连续,但由于定积分的被积函数在某一点处的函数值是完全无所谓的,所以可以把结论②中所说的“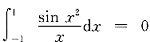 ”改写为“
”改写为“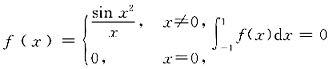 ”.这样一来,f(x)在区间[-1,1]上连续,且为奇函数,根据以上定理可知,结论②正确.
”.这样一来,f(x)在区间[-1,1]上连续,且为奇函数,根据以上定理可知,结论②正确.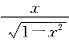 在x=1,x=-1处没有定义.现在算一下
在x=1,x=-1处没有定义.现在算一下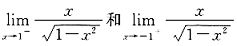 ,这两个极限只要有一个是∞,就说明
,这两个极限只要有一个是∞,就说明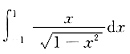 是反常积分.通过计算可知
是反常积分.通过计算可知 和
和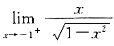 这两个极限都是∞,所以
这两个极限都是∞,所以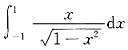 是反常积分,而不是定积分.
是反常积分,而不是定积分.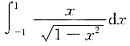 等于0.
等于0.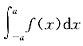 是一个反常积分,如果f(x)在除x=±c外的区间[-a,a]上连续(其中c为[-a,a]上的点),且f(x)在除±c外的区间[-a,a]上是一个奇函数,且
是一个反常积分,如果f(x)在除x=±c外的区间[-a,a]上连续(其中c为[-a,a]上的点),且f(x)在除±c外的区间[-a,a]上是一个奇函数,且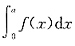 的值是一个常数,则反常积分
的值是一个常数,则反常积分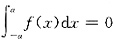 .
.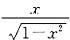 在区间[-1,1]上除了x=±1连续(也就是说
在区间[-1,1]上除了x=±1连续(也就是说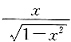 在区间(-1,1)上连续),这是毫无疑问的,
在区间(-1,1)上连续),这是毫无疑问的,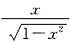 在区间(-1,1)上是一个奇函数也对.
在区间(-1,1)上是一个奇函数也对.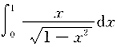 是否等于一个常数.通过计算可知答案是常数,所以结论③正确.
是否等于一个常数.通过计算可知答案是常数,所以结论③正确.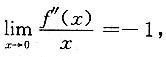 则______.
则______.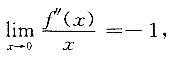 所以
所以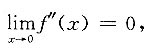 即f"(0)=0.又
即f"(0)=0.又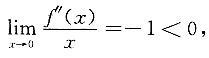 由极限的保号性,存在δ>0,当0<|x|<δ时,有
由极限的保号性,存在δ>0,当0<|x|<δ时,有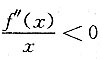 ,即当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,所以(0,f(0))为曲线y=f(x)的拐点,选C.
,即当x∈(-δ,0)时,f"(x)>0,当x∈(0,δ)时,f"(x)<0,所以(0,f(0))为曲线y=f(x)的拐点,选C.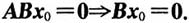
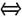 Bx=0和ABx=0是同解方程组.故应选C.
Bx=0和ABx=0是同解方程组.故应选C.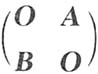 的伴随矩阵为
的伴随矩阵为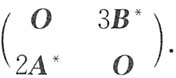

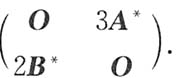

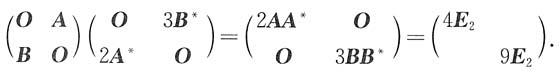

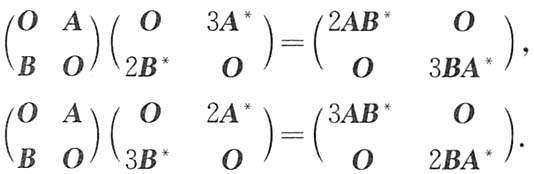
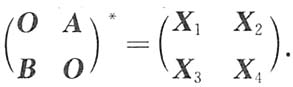
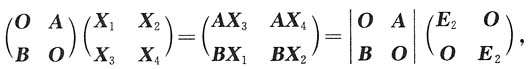
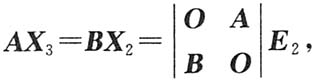
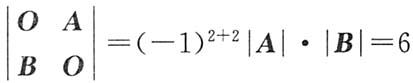 ,故得
,故得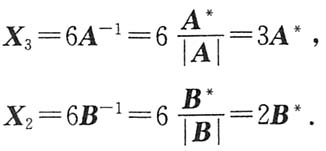
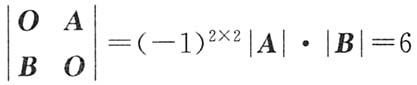 ,则
,则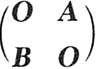 可逆,于是
可逆,于是
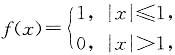 则f{f[f(x)]}=
则f{f[f(x)]}=
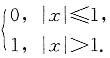
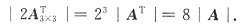

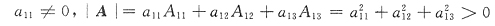
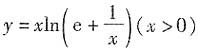 的渐近线方程为______.
的渐近线方程为______.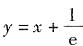
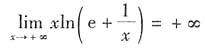 ,因此无水平渐近线.
,因此无水平渐近线.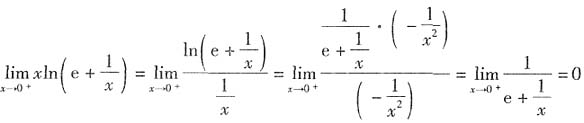 ,
,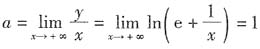 ,
,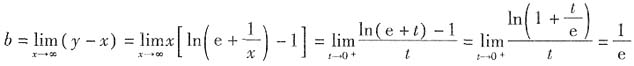 ,
,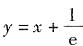 .
.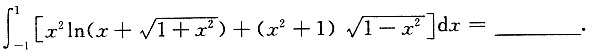
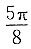
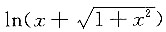 为奇函数,所以
为奇函数,所以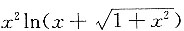 为奇函数,
为奇函数,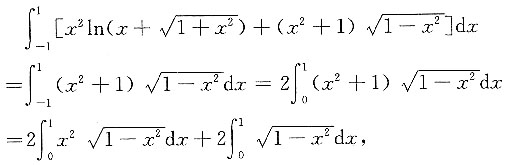
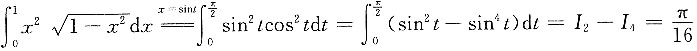 ,
,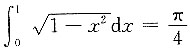 ,所以原式=
,所以原式=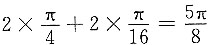 .
.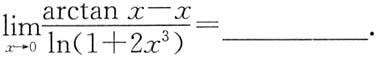
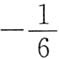 .
.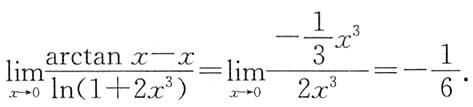
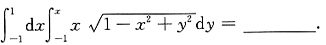
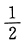
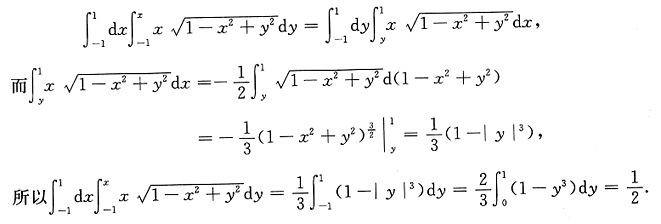
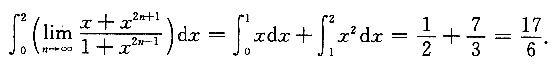
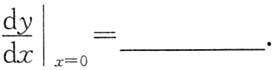
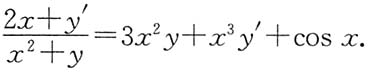
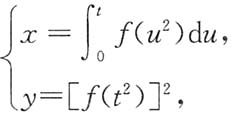 其中f(u)具有二阶导数,且f(u)≠0,求
其中f(u)具有二阶导数,且f(u)≠0,求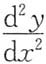 .
.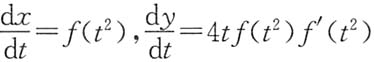 ,所以
,所以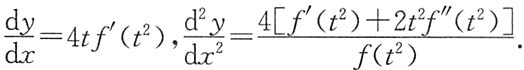
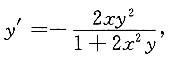
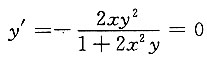 得x=0,
得x=0,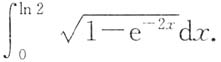
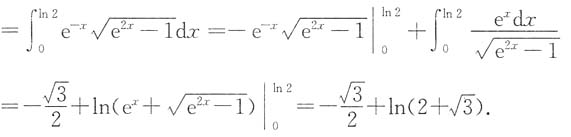
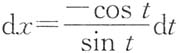 ,
,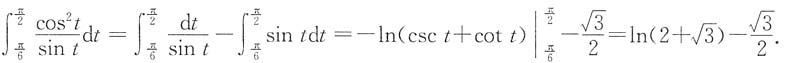
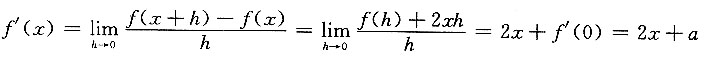 得
得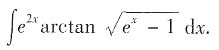

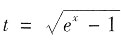 ,化简过后,利用分部积分逐步求解.最后求得关于t的表达式后,记得将
,化简过后,利用分部积分逐步求解.最后求得关于t的表达式后,记得将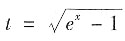 再代回去.(求解过程略)
再代回去.(求解过程略)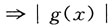 连续.但g(x)可导
连续.但g(x)可导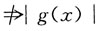 可导.当|g(x)|可导,由可导性运算法则知F(x)可导,当|g(x)|不可导(或不知是否可导时),则按定义考察F(x)的可导性.
可导.当|g(x)|可导,由可导性运算法则知F(x)可导,当|g(x)|不可导(或不知是否可导时),则按定义考察F(x)的可导性.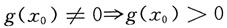 (或g(x0)<0),由g(x)在x=x0连续
(或g(x0)<0),由g(x)在x=x0连续
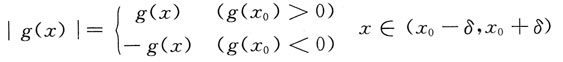
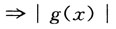 与g(x)在x=x0有相同的可导性,即|g(x)|在x=x0可导,
与g(x)在x=x0有相同的可导性,即|g(x)|在x=x0可导,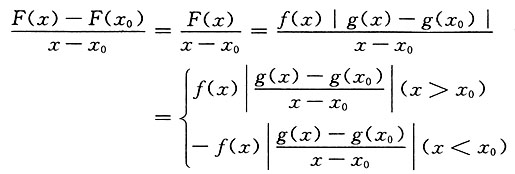
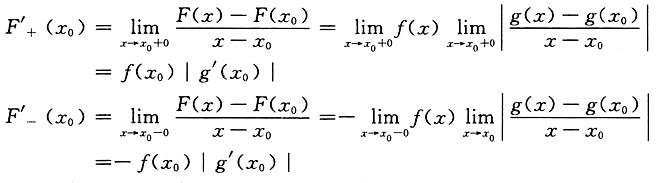
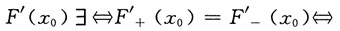
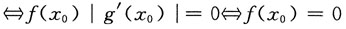 或g'(x0)=0.
或g'(x0)=0.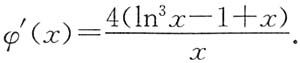
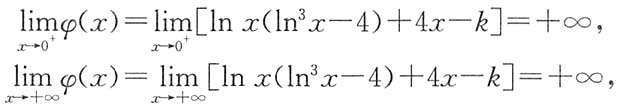
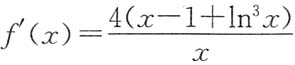 ,不难看出x=1是f(x)的驻点.又f"(x)=
,不难看出x=1是f(x)的驻点.又f"(x)=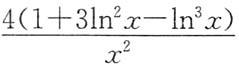 ,f"(x)>0,所以f(1)=4为f(x)的最小值.
,f"(x)>0,所以f(1)=4为f(x)的最小值.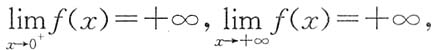
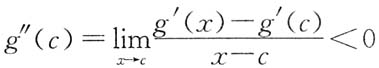 ,而g'(c)=0,故
,而g'(c)=0,故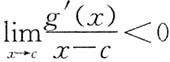 .由极限的保号性,
.由极限的保号性,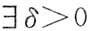 ,当x∈(c-δ,c)时,有
,当x∈(c-δ,c)时,有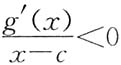 ,即g'(x)>0,从而g(x)在(c-δ,c)上单增;当x∈(c,c+δ)时,有
,即g'(x)>0,从而g(x)在(c-δ,c)上单增;当x∈(c,c+δ)时,有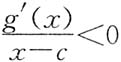 ,即g'(x)<0,从而g(x)在(c-δ,c)上单减.
,即g'(x)<0,从而g(x)在(c-δ,c)上单减.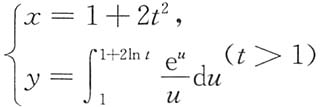 所确定,求
所确定,求