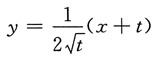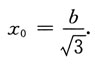一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 下列曲线中有渐近线的是
A.y=x+sinx.
B.y=x
2+sinx.
C.
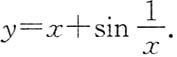
D.
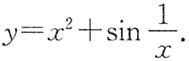
A B C D
C
[解析] 对于
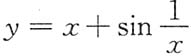
,可知
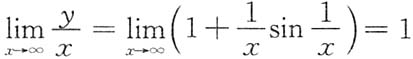
.又
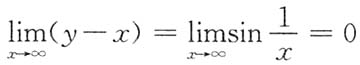
,所以有斜渐近线y=x,因此应选C.
2. 曲线
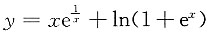
的渐近线有______
- A.1条水平的,1条斜的,1条铅直的.
- B.2条水平的,没有斜的,1条铅直的.
- C.没有水平的,2条斜的,1条铅直的.
- D.1条水平的,1条斜的,没有铅直的.
A B C D
C
[解析] 因
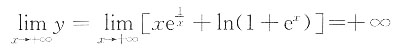
,
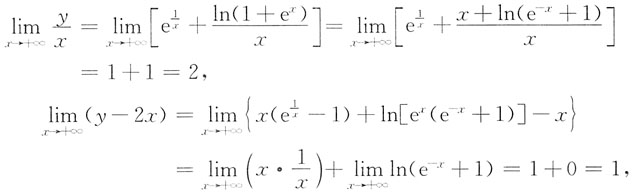
所以有1条斜渐近线y=2x+1(沿x→+∞方向).
又

所以又有1条斜渐近线y=x+1(沿x→-∞方向).
综上,曲线左右各有一条斜渐近线,所以就没有水平渐近线.
又
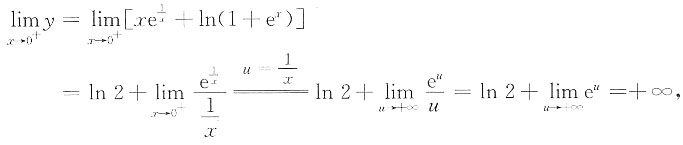
所以有1条铅直渐近线.选C.
3. 若A,A*和B均是n阶非零矩阵,且AB=0,则必有r(B)=
- A.1.
- B.2.
- C.n-1.
- D.条件不够不能确定.
A B C D
A
[解析] A,B是n阶矩阵,且AB=O,则有
(1)B的列向量是齐次方程组Ax=0的解
(2)秩r(A)+r(B)≤n
由(1),对于AB=O,B≠O知Ax=0有非零解,从而秩r(A)<n.又因A*≠O知有代数余子式A
ij≠0,即A中有n-1阶子式非零.于是r(A)=n-1.再根据(2)知r(B)≤1,又因B≠O.故必有r(B)=1.故应选A.
关于r(A)也可由
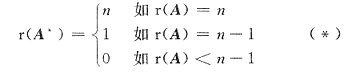
可知r(A*)=1.
因为A*≠0,有r(A*)≥1,于是r(A)≥n-1,那么再由AB=O,B≠O知r(A)<n,因此只能是r(A)=n-1.故r(B)=1,应选A.
4. 设函数f(u,v)满足
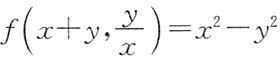
,则
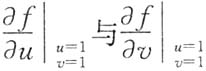
依次是
A.

B.
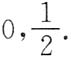
C.
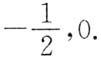
D.

A B C D
D
[解析] 解法1 先求出f(u,v).
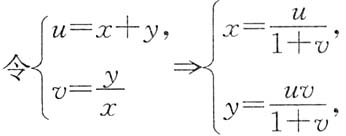
于是
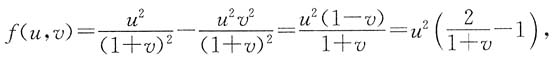
因此
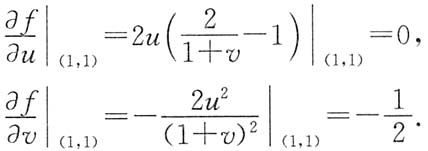
解法2 不必先求出f(u,v).
由

即(u,v)=(1,1)对应
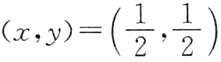
,
现对
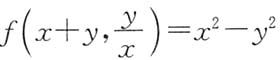
两边分别对x,y求偏导数得

上两式中令
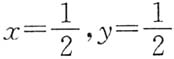
得
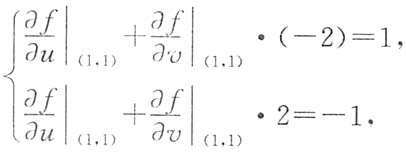
由此解出
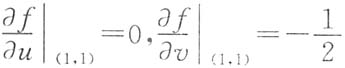
.选D.
5. 双纽线(x
2+y
2)
2=x
2-y
2所围成的区域面积可用定积分表示为______
A.
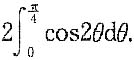
B.
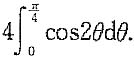
C.
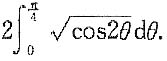
D.
A B C D
6. 设

是3阶可逆矩阵,B是3阶矩阵,满足

则B有特征值______
- A.1,-1,-4.
- B.1,1,4.
- C.1,2,-2.
- D.1,2,2.
A B C D
C
[解析] 由题设条件得
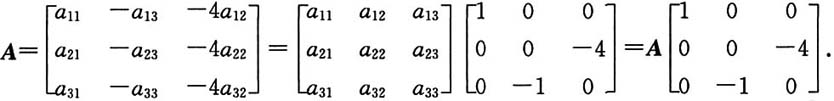
A是可逆矩阵,故有
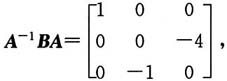
即
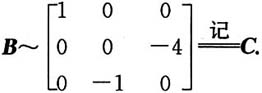
相似矩阵有相同的特征值,故C和B有相同的特征值.
因为
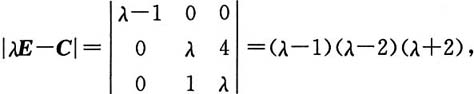
故B有特征值为λ
1=1,λ
2=2,λ
3=-2,故应选C.
或由
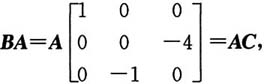
两边取行列式,得|BA|=|AC|,
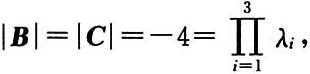
故应选C.
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.求下列方程所确定函数的全微分:3. 设
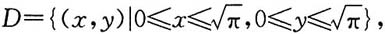
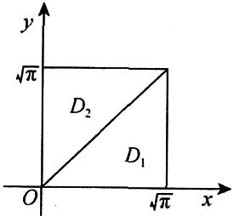
计算二重积分
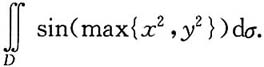
解:D是一块矩形域,如图所示.
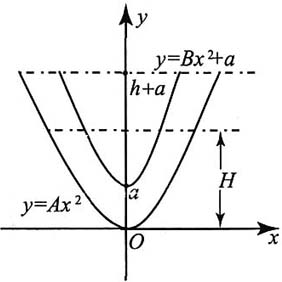
4. 设一旋转抛物面的容器内盛有高为H的液体,把另一同轴的旋转抛物面体沿旋转轴方向压入(不进水)盛水的上述容器内,浸没深度为h,问抛物面的容器内液面上升多少?
解:设旋转抛物面的容器和旋转抛物面体分别由xOy平面上的抛物线y
1=Ax
2,y
2=Bx
2+a绕y轴旋转而成.
如图所示,设V
1为抛物面容器中的液体被第二个抛物面体所排开的体积,则
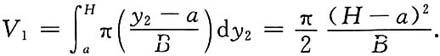
设被挤上升的液体体积为V
2,则
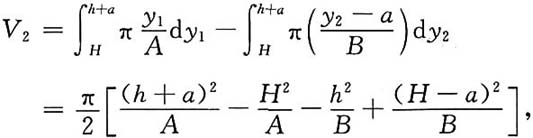
由V
1=V
2,得
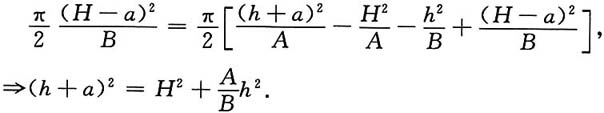
因为h+a>0,则
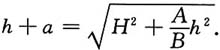
故液面上升高度为

5. 在(0,+∞)内作y=f(x)的图形;
解:
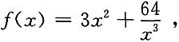
考察(0,+∞)内的函数特性.
因为f'(x)=6x-192x
-4=6x(1-32x
-5),
由f'(x)=6x-192x
-4=0,得唯一驻点x
1=2.
又f"(x)=6+768x
-5>0,曲线为下凸,
x
1=2为极小值点,极小值为f(2)=20.
因为
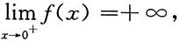
所以f(x)在(0,+∞)内有垂直渐近线x=0.
因为
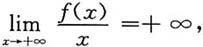
所以f(x)在(0,+∞)内没有斜渐近线.
由以上分析,得下图.
6. 证明:
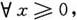
3x
5-20x
3+64≥0.
证明:由于f(x)=3x
2+64x
-3在(0,+∞)上连续且有唯一极值点x=2,且
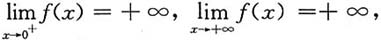
所以x=2也是f(x)=3x
2+64x
-3在(0,+∞)内的最小值点,最小值为f(2)=20.
所以,
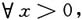
f(x)=3x
2+64x
-3≥20,即3x
5-20x
3+64≥0
7. 求微分方程y"+y=f(x)满足初始条件:y(0)=0,y'(0)=1的特解,其中连续函数f(x)满足条件
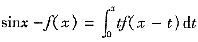
。
解:由于
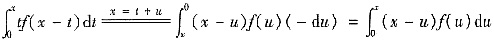
,则题设条件可表示为
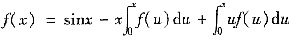
。
在两边对x求导,得
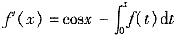
;
再在两边对x求导,整理可得f"(x)+f(x)=-sinx,且f(0)=0,f'(0)=1。
解上述方程组得
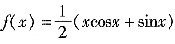
。可见原方程为
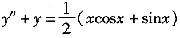
故对应齐次方程的通解为y=C
1cosx+C
2sinx,C
1,C
2为任意常数,且特解可设为y
*=x(b
1x+b
2)cosx+x(b
3x+b
4)sinx,代入方程后得
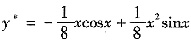
。再根据初始条件
y(0)=0,y'(0)=1得所求解为

。
[考点] 在初始条件下,二阶微分方程的解的应用。
8. 设矩阵A=

,B=
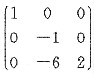
.
试判断A和B是否相似,若相似,求出可逆矩阵X,使得X
-1AX=B.
解:由∣λE-A∣=
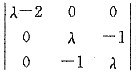
=(λ-2)(λ-1)(λ+1),
得A的特征值为2,1,-1.因此A相似于
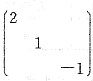
.
进而求得对应于2,1,-1的特征向量分别为
令P=(η
1,η
2),η
3),则有P
-1AP=
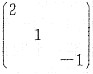
.
又因为B是下三角矩阵,所以特征值为2,1,-1.B也相似于
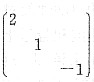
.
进而求得对应2,1,-1的特征向量分别为
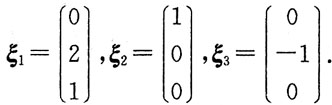
.
令Q=(ξ
1,ξ
2,ξ
3),则Q
-1BQ=
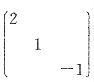
.
因此P
-1AP=Q
-1BQ,所以B=QP
-1APQ
-1=(PQ
-1)
-1A(PQ
-1),
令X=PQ
-1=
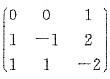
,X即为所求.
[考点] 矩阵相似的判别.
将A,B分别相似对角化,与同一个对角阵相似,再根据相似的传递性,得到A,B相似.
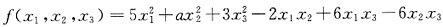 的矩阵合同于
的矩阵合同于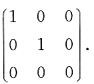
9. 求常数a的值;
解:令
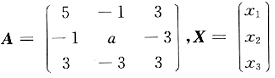
,则f(x
1,x
2,x
3)=X
TAX.
因为A与
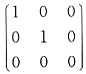
合同,所以r(A)=2<3,故|A|=0.
由
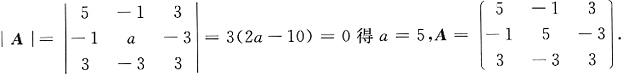
10. 用正交变换法化二次型f(x
1,x
2,x
3)为标准形.
解:由
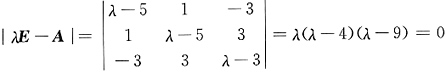
得λ
1=0,λ
2=4,λ
3=9.
由(0E-A)X=0得
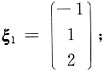
由(4E-A)X=0得
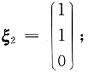
由(9E-A)X=0得
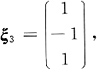
单位化得
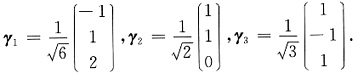
令

则
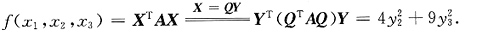
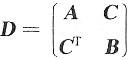 为正定矩阵,其中A,B分别为m阶,n阶实对称矩阵,C为m×n矩阵.
为正定矩阵,其中A,B分别为m阶,n阶实对称矩阵,C为m×n矩阵.11. 计算P
TDP,其中
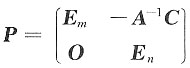
,E
m,E
n分别为m阶,n阶单位矩阵;
解:因

,有
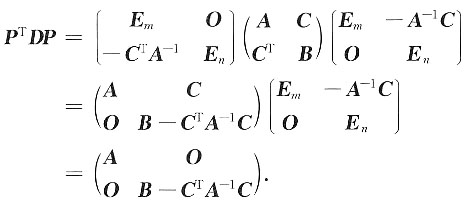
12. 利用上小题的结果判断矩阵B-C
TA
-1C是否为正定矩阵,并说明理由.
解:矩阵B-C
TA
-1C是正定矩阵.
事实上,由|P|=1知矩阵P可逆,由上小题的结果可知,矩阵D合同于矩阵
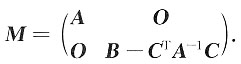
又D为正定矩阵,可知矩阵M为正定矩阵.
直接验算知B-C
TA
-1C为对称矩阵.
对x=(0,0,…,0)
T及任意的y=(y
1,y
2,…,y
n)
T≠0,有
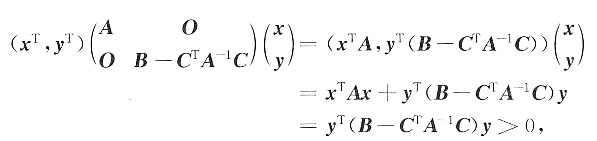
故B-C
TA
-1C为正定矩阵.
[考点] 本题主要考查分块矩阵的运算以及正定矩阵的判定.第一问直接利用分块矩阵的运算法则进行计算;第二问是讨论抽象矩阵的正定性,一般用定义.
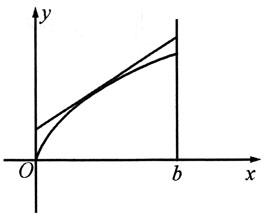
13. 设b>0,求x
0∈(0,b),使得由曲线
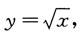
过点
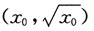
的曲线
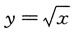
的切线以及直线x=b和y轴所围成的平面图形绕x轴旋转一周所得旋转体的体积V最小.
解:曲线
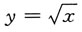
在点
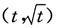
的切线方程是

即
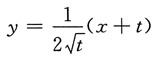
其中t∈(0,b).
所求问题等价于求此切线与直线x=b,y轴和x轴所围成平面图形绕x轴旋转一周所得旋转体的体积的最小值点.即求

在(0,b)的最小值点.
求V'(t)
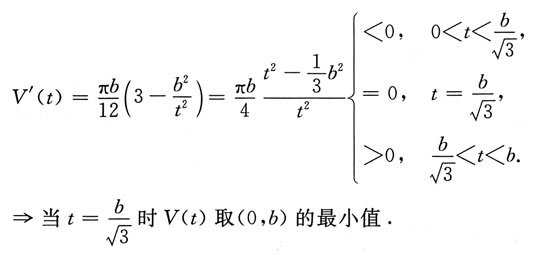
因此,所求的
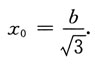
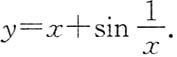
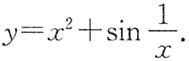
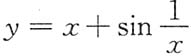 ,可知
,可知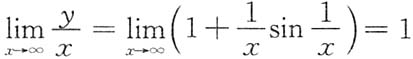 .又
.又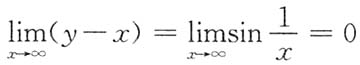 ,所以有斜渐近线y=x,因此应选C.
,所以有斜渐近线y=x,因此应选C.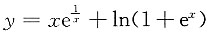 的渐近线有______
的渐近线有______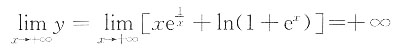 ,
,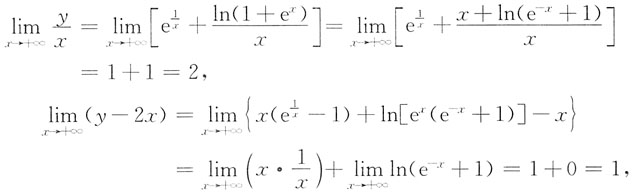

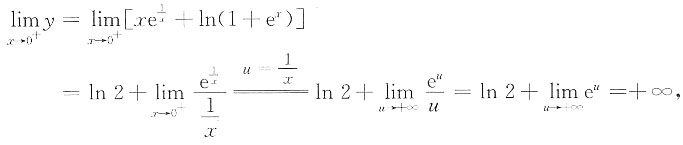
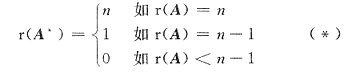
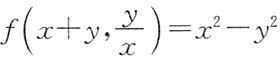 ,则
,则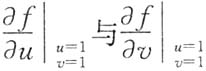 依次是
依次是
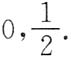
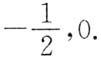

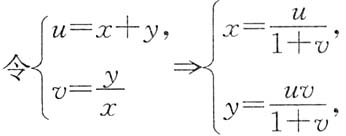
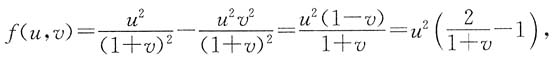
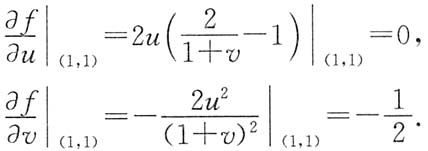
 即(u,v)=(1,1)对应
即(u,v)=(1,1)对应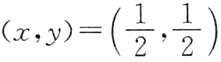 ,
,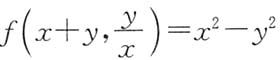 两边分别对x,y求偏导数得
两边分别对x,y求偏导数得
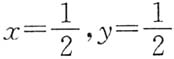 得
得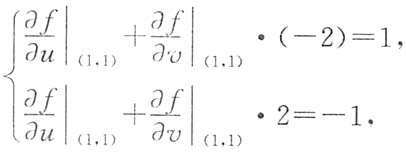
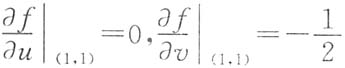 .选D.
.选D.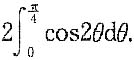
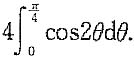
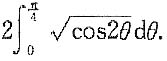
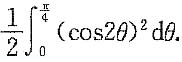
 是3阶可逆矩阵,B是3阶矩阵,满足
是3阶可逆矩阵,B是3阶矩阵,满足 则B有特征值______
则B有特征值______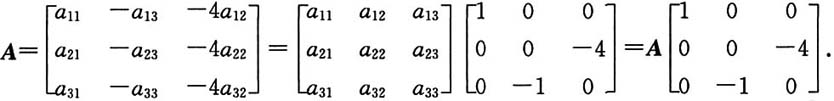
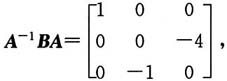 即
即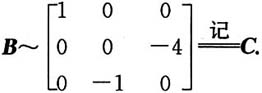
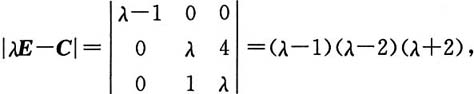 故B有特征值为λ1=1,λ2=2,λ3=-2,故应选C.
故B有特征值为λ1=1,λ2=2,λ3=-2,故应选C.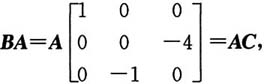 两边取行列式,得|BA|=|AC|,
两边取行列式,得|BA|=|AC|,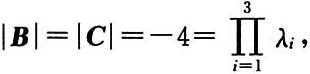 故应选C.
故应选C. ,已知
,已知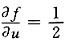 ,则
,则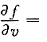
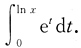

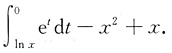
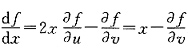 .又由于
.又由于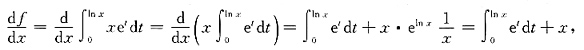
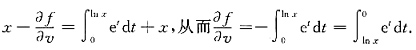
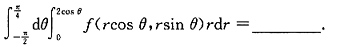
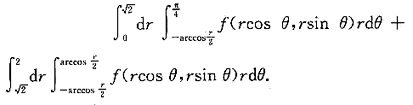
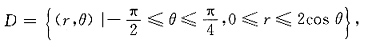
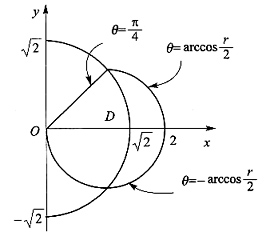
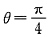 围成的图形(如下图).作以O为圆心且穿过D的同心圆r=C,当
围成的图形(如下图).作以O为圆心且穿过D的同心圆r=C,当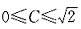 时,r=C从r=2cosθ(θ<0),即
时,r=C从r=2cosθ(θ<0),即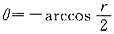 进入D,从
进入D,从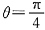 穿出D;当
穿出D;当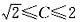 时,r=C从r=2cosθ(θ<0),即
时,r=C从r=2cosθ(θ<0),即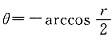 进入D,从r=2cosθ(θ>0),即
进入D,从r=2cosθ(θ>0),即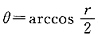 穿出D.故原二次积分交换积分次序后为
穿出D.故原二次积分交换积分次序后为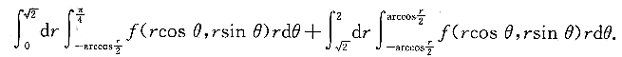
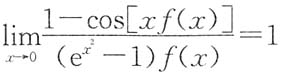 ,则f(0)=______.
,则f(0)=______.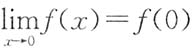 .由题设
.由题设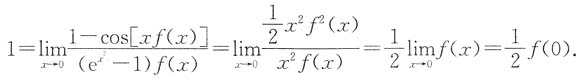
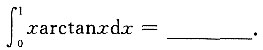
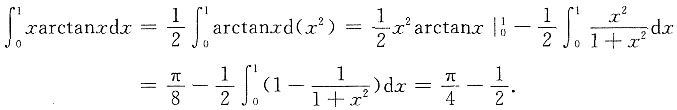
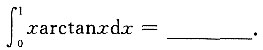
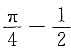
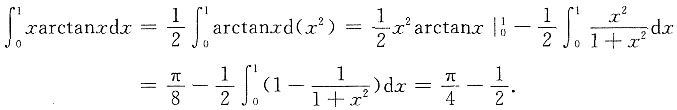
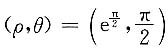 处的切线的直角坐标方程为______.
处的切线的直角坐标方程为______.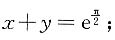
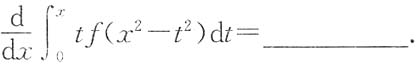
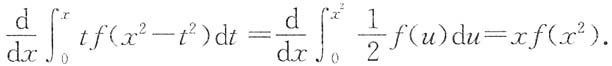
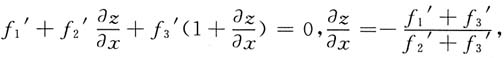
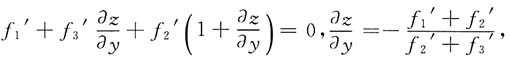
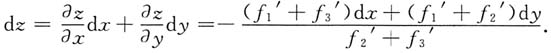
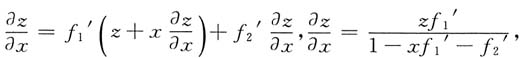
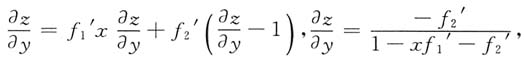
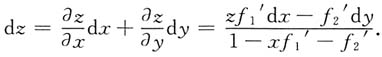
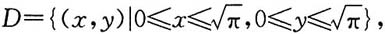 计算二重积分
计算二重积分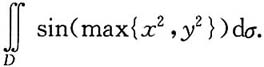
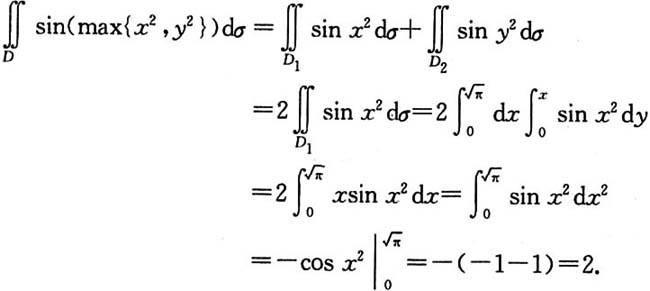
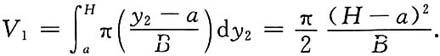
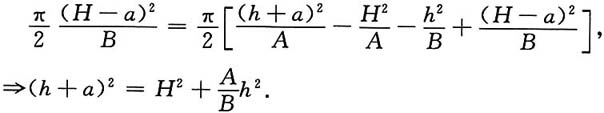
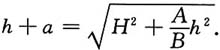

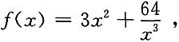 考察(0,+∞)内的函数特性.
考察(0,+∞)内的函数特性.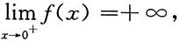 所以f(x)在(0,+∞)内有垂直渐近线x=0.
所以f(x)在(0,+∞)内有垂直渐近线x=0.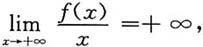 所以f(x)在(0,+∞)内没有斜渐近线.
所以f(x)在(0,+∞)内没有斜渐近线.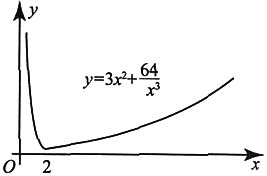
 3x5-20x3+64≥0.
3x5-20x3+64≥0. 所以x=2也是f(x)=3x2+64x-3在(0,+∞)内的最小值点,最小值为f(2)=20.
所以x=2也是f(x)=3x2+64x-3在(0,+∞)内的最小值点,最小值为f(2)=20.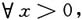 f(x)=3x2+64x-3≥20,即3x5-20x3+64≥0
f(x)=3x2+64x-3≥20,即3x5-20x3+64≥0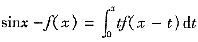 。
。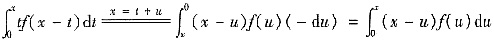 ,则题设条件可表示为
,则题设条件可表示为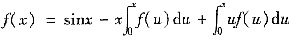 。
。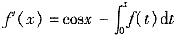 ;
;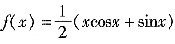 。可见原方程为
。可见原方程为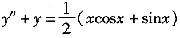
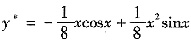 。再根据初始条件
。再根据初始条件 。
。 ,B=
,B=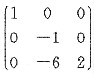 .
.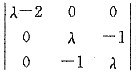 =(λ-2)(λ-1)(λ+1),
=(λ-2)(λ-1)(λ+1),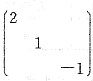 .
.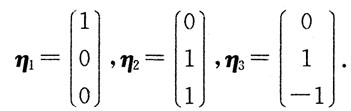
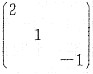 .
.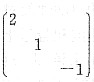 .
.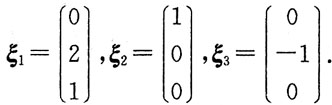 .
.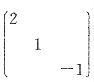 .
.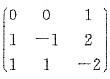 ,X即为所求.
,X即为所求.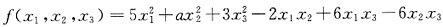 的矩阵合同于
的矩阵合同于
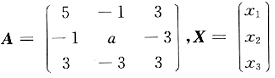 ,则f(x1,x2,x3)=XTAX.
,则f(x1,x2,x3)=XTAX.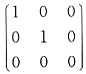 合同,所以r(A)=2<3,故|A|=0.
合同,所以r(A)=2<3,故|A|=0.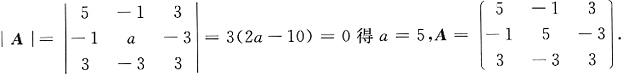
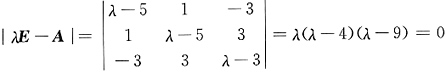 得λ1=0,λ2=4,λ3=9.
得λ1=0,λ2=4,λ3=9.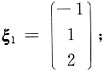
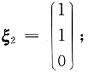
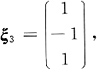
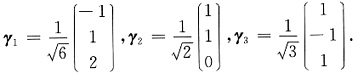

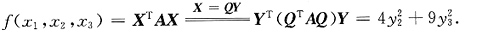
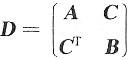 为正定矩阵,其中A,B分别为m阶,n阶实对称矩阵,C为m×n矩阵.
为正定矩阵,其中A,B分别为m阶,n阶实对称矩阵,C为m×n矩阵.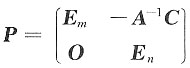 ,Em,En分别为m阶,n阶单位矩阵;
,Em,En分别为m阶,n阶单位矩阵; ,有
,有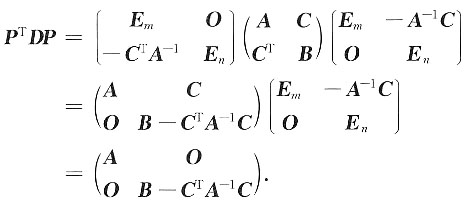
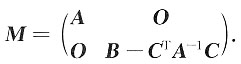
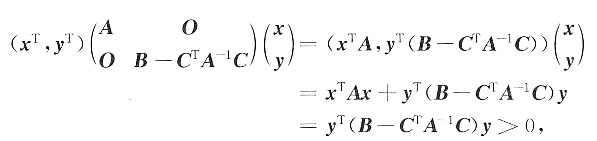
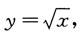 过点
过点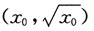 的曲线
的曲线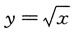 的切线以及直线x=b和y轴所围成的平面图形绕x轴旋转一周所得旋转体的体积V最小.
的切线以及直线x=b和y轴所围成的平面图形绕x轴旋转一周所得旋转体的体积V最小.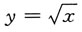 在点
在点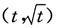 的切线方程是
的切线方程是