一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.2. 设函数f(x)单调,且f'(0)≠0.若
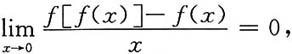
则______
- A.f(0)+f'(0)=-1.
- B.f(0)+f'(0)=1.
- C.f(0)+f'(0)=0.
- D.f(0)+f'(0)=2.
A B C D
B
[解析]
思路一: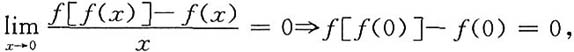
即
f[f(0)]=f(0).
因为f(x)单调,则f(x)在x=0点某邻域内存在反函数f
-1.
由此可得f(0)=f
-1[f(0)]=0.
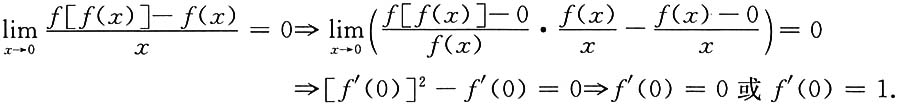
依题意有f(0)=0,f'(0)=1,f(0)+f'(0)=1.
思路二: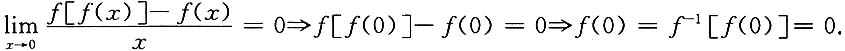
假设f(x)连续可导,则
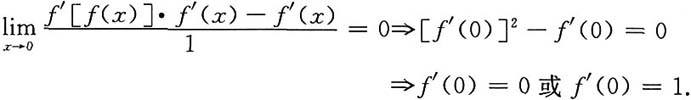
依题意有f(0)=0,f'(0)=1,f(0)+f'(0)=1.
3. 设二阶可导函数f(x)满足f(1)=f(-1),f(0)=-1且f"(x)>0,则______
A.

B.

C.
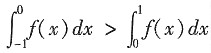
D.

A B C D
B
[解析] f(x)为偶函数时满足题设条件,此时
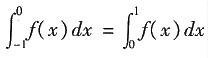
,排除C,D.取f(x)=2x
2-1满足条件,则
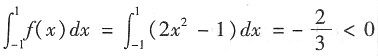
,选B.
4. α
1,α
2,α
3是四元非齐次线性方程组Ax=b的三个解向量,且r(A)=3,α
1=(1,2,3,4)
T,α
2+α
3=(0,1,2,3)
T.c表示任意常数,则线性方程组Ax=b的通解x=______.
A.
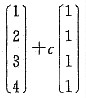
B.
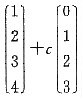
C.
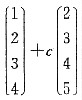
D.

A B C D
C
[考点] 非齐次线性方程组解的结构.
根据非齐次线性方程组解的结构,依次求出其导出组的基础解系和自身的一个特解即可.
解:根据线性方程组解的性质,可知
2α1-(α2+α3)=(α1-α2)+(α1-α3)
是非齐次线性方程组Ax=b导出组Ax=0的一个解.因为r(A)=3,所以Ax=0的基础解系含4-3=1个解向量,而2α
1-(α
2+α
3)=(2,3,4,5)
T≠0,故是Ax=0的一个基础解系.因此AX=b的通解为
α1+c(2α1-α2-α3)=(1,2,3,4)T+c(2,3,4,5)T,
即C选项正确.对于其他几个选项,A选项中
(1,1,1,1)T=α1-(α2+α3),
选项B中
(0,1,2,3)T=α2+α3,
选项D中
(3,4,5,6)T=3α1-2(α2+α3),
都不是Ax=b的导出组的解.所以A、B、D项均不正确.
故应选C.
5. 设函数z=z(x,y)由方程
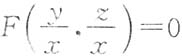
确定,其中F为可微函数,且F'
2≠0,则
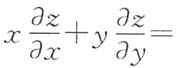
A B C D
B
[解析] 在等式
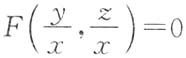
两端关于x求偏导,得
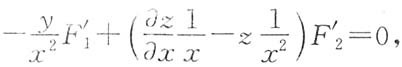
①
在等式
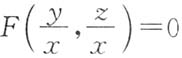
两端关于y求偏导,得
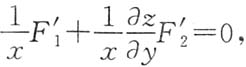
②
①×x
2+②×xy得
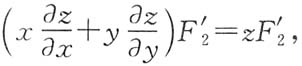
所以
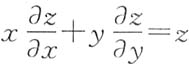
.即正确选项为B.
还可以利用一阶全微分形式不变性求解,留给读者自练.
7. 设f(x)在[a,b]连续,则下列结论中正确的个数为
①f(x)在[a,b]的任意子区间[a,β]上
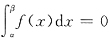
,则
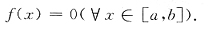
②f(x)≥0(x∈[a,b]),又
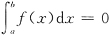
,则f(x)=0(x∈[a,b]).
③[a,β]
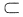
[a,b],则
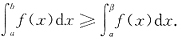
A B C D
C
[解析] 我们要逐一分析.
结论①正确.由条件

结论②正确.由条件
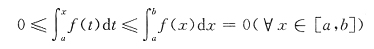
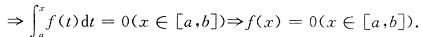
结论③错误,如下图所示,由定积分几何意义知,
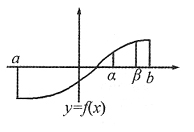
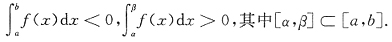
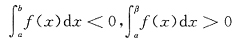
,其中[α,β]
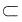
[a,b].
因此选C.
8. 设F(x)是连续函数f(x)的一个原函数,“
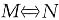
”表示“M的充分必要条件是N”,则必有
A.F(x)是偶函数
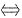
f(x)是奇函数.
B.F(x)是奇函数
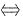
f(x)是偶函数.
C.F(x)是周期函数
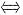
f(x)是周期函数.
D.F(x)是单调函数

f(x)是单调函数.
A B C D
二、填空题1. 已知
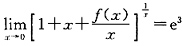
,则
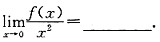
2
[解析] 因为
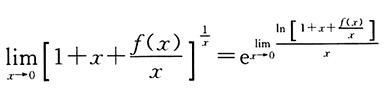
,由题意得
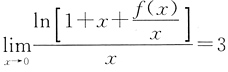
.
由于
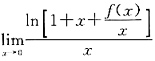
存在,
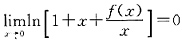
,故当x→0时,
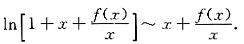
于是
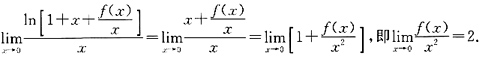
2.
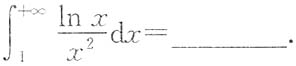
1.
[解析]
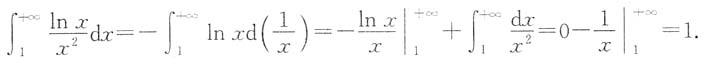
3. 设ρ=a(1+cosθ),则

[解析] 将ρ=a(1+cosθ)化为参数方程
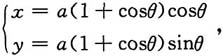
θ为参数.
x'
θ=-asinθcosθ-a(1+cosθ)sinθ=-a(sinθ+sin2θ),
y'
θ=-asin
2θ+a(1+cosθ)cosθ=a(cosθ+cos2θ).
故
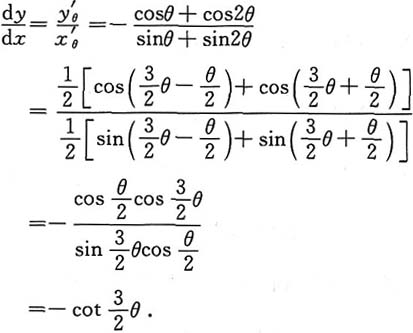
4. 方程yy"=1+y'
2满足初始条件y(0)=1,y'(0)=0的通解为______.
±x
[考点] 高阶微分方程的解
[解析] 令y'=p,则
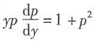
,即
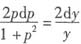
,
解得ln(1+p
2)=lny
2+lnC
1,则1+p
2=C
1y
2,
由y(0)=1,y'(0)=0得
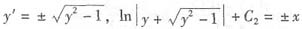
,
由y(0)=1得C
2=0,所以特解为
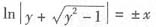
.
5.
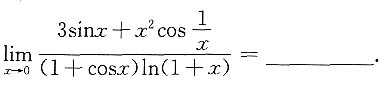
6. 设α
1,α
2,α
3均为三维列向量,记矩阵
A=(α
1,α
2,α
3),B=(α
1+α
2+α
3,α
1+2α
2+4α
3,α
1+3α
2+9α
3).如果|A|=1,那么|B|=______.
2.
[解析] 解法1 利用行列式的性质计算.
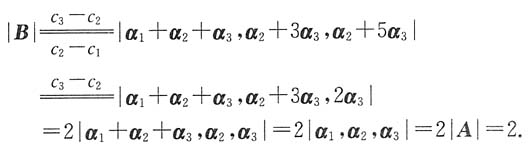
解法2 利用矩阵的性质计算.
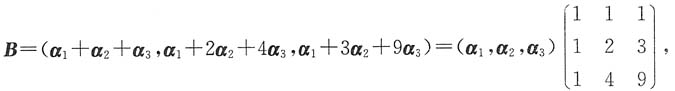
则

三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.1. 计算
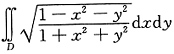
,其中D={(x,y)|x
2+y
2≤1,x≥0,y≥0}.
[解]
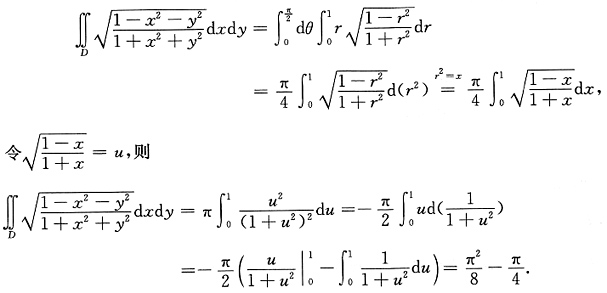
2. 设f(u,v)有二阶连续偏导数,且满足
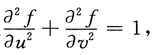
又
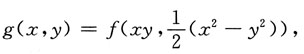
求
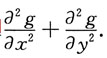
[解] 由复合函数求导法得

现将①,②式相加得
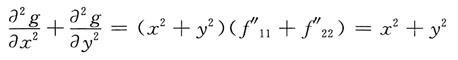
其中由条件知f"
11+f"
22=1.
3. 设f(x)在[a,b]上可导,且ab>0,试证:存在一个ξ∈(a,b),使
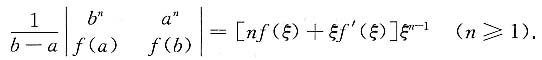
证明:令F(x)=x
nf(x),由拉格朗日定理,得b
nf(b)-a
nf(a)=[nξ
n-1f(ξ)+ξ
nf'(ξ)](b-a),ξ∈(a,b),即
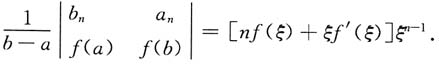
4. 设e<a<b<e
2.证明
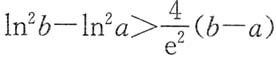
.
证法1 设
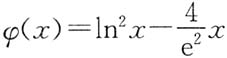
,则
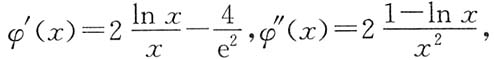
所以当x>e时,φ"(x)<0,故φ'(x)单调减少,从而当e<x<e
2时,
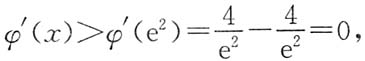
即当e<x<e
2时,φ(x)单调增加.
因此当e<a<b<e
2时,φ(b)>φ(a),
即
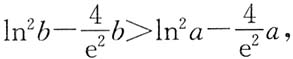
故
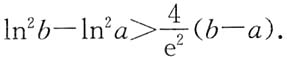
证法2 原不等式等价于:
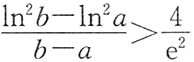
,左端可看作函数f(x)=ln
2x在[a,b]上的拉格朗日中值定理的形式,故

,a<ξ<b.下面对ξ作估计:
令
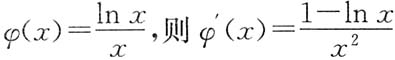
,当x>e时,φ'(x)<0,则φ(x)在(e,+∞)上单调减少,故
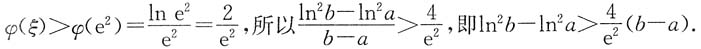
5. 设f(x)在[1,+∞)上连续且可导,若曲线y=f(x),直线x=1,x=t(t>1)与x轴围成的平面区域绕x轴旋转一周所得的旋转体的体积为
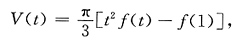
且
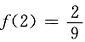
,求函数y=f(x)的表达式.
[解] 由旋转体的体积公式得
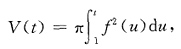
由已知条件得
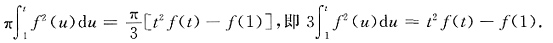
等式两边对t求导得
3f
2(t)=2tf(t)+t
2f
'(t),
于是有x
2y
'=3y
2-2xy,变形得
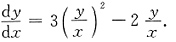
令
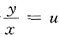
,则有
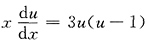
,分离变量并两边积分得
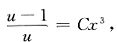
即y-x=Cx
3y,
由
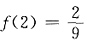
得C=-1,故
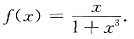
6. 设a为正常数,f(x)=xe
a-ae
x-x+a.证明:当x>a时,f(x)<0.
[证]f(a)=0,f'(x)=e
a-ae
x-1,f"(x)=-ae
x<0.以下证明f'(a)<0.
令φ(a)=f'(a)=e
a-ae
a-1,φ(a)|
a=0=0,φ'(a)=-ae
a<0,
所以φ(a)<0(a>0),即f'(a)<0(a>0).
将f(x)在x=a处按二阶泰勒公式展开:
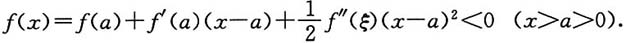
证毕.
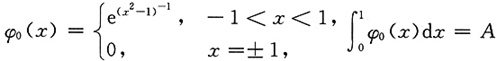 ,令
,令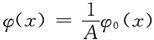 ,又有f(x)在[-1,1]上连续,若φn(x)=nφ(nx)(n=1,2,…),
,又有f(x)在[-1,1]上连续,若φn(x)=nφ(nx)(n=1,2,…),7. 求极限

[解析] 记
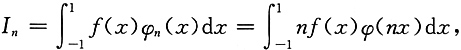
令nx=u,则
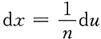
,故
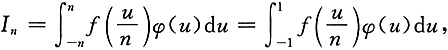
注意到φ(x)为偶函数,并且由于f(x)在[-1,1]上连续,φ(x)在[-1,1]上不变号,由积分中值定理,得
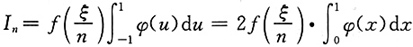
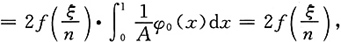
其中ξ∈(-1,1),再次由f(x)的连续性,得到
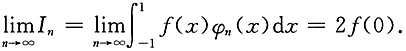
8. 设x
0∈(-1,1),求极限
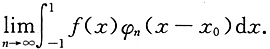
[解析] 记
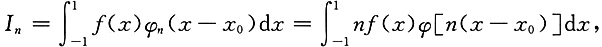
令n(x-x
0)=t,则
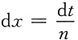
,于是
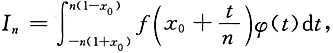
注意到当n足够大时有(-1,1)

[-n(1+x
0),n(1-x
0)],并应用积分中值定理,得到
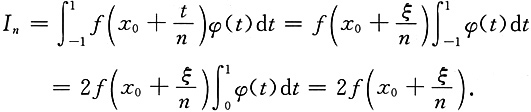
其中ξ∈(-1,1),再次由f(x)的连续性,得
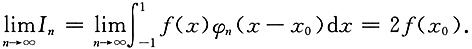
9. 已知f(x)是周期为5的连续函数,它在x=0的某个邻域内满足关系式
f(1+sinx)-3f(1-sinx)=8x+α(x),
其中α(x)是当x→0时比x高阶的无穷小,且f(x)在x=1处可导,求曲线y=f(x)在点(6,f(6))处的切线方程.
解 由
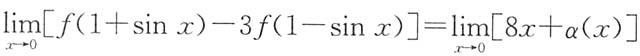
,
得f(1)-3f(1)=0,故f(1)=0.又
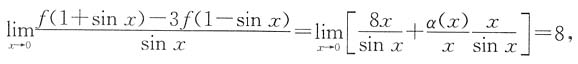
设sinx=t,则有
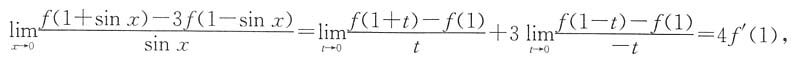
所以f'(1)=2.
由于f(x+5)=f(x),所以
f(6)=f(1)=0,f'(6)=f'(1)=2,
故所求的切线方程为y=2(x-6),即2x-y-12=0.
[解析] 本题综合涉及函数的周期性、连续性、极限、导数定义及曲线的切线等内容,问题的关键点在于求出f'(1),而又只能由导数的定义求f'(1),这也是本题的难点所在.
10. 设常数a>0,求函数
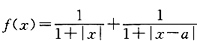
在(-∞,+∞)内的最值.
[解]
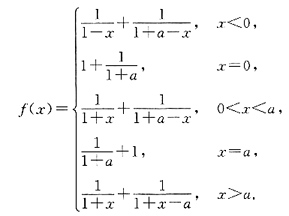
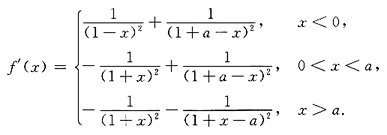
显然,f(x)的不可导点为x=0和x=a,驻点为
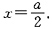
可能极值点有三个,通过验证可知只有极大值点x=0,对应的极大值为
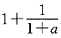
.
接下来求区间端点处的极限值:
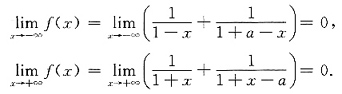
所以,
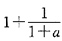
是f(x)在区间(-∞,+∞)内的最大值,f(x)在区间(-∞,+∞)内无最小值.
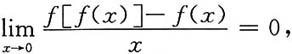 则______
则______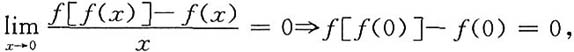 即
即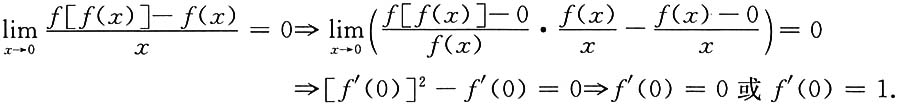
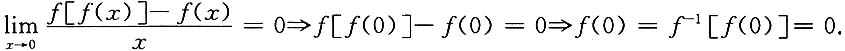
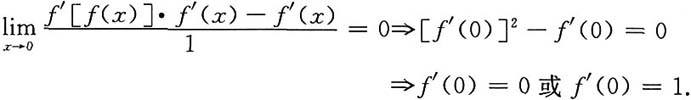


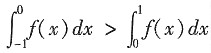

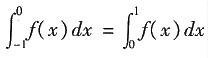 ,排除C,D.取f(x)=2x2-1满足条件,则
,排除C,D.取f(x)=2x2-1满足条件,则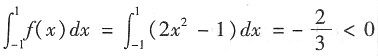 ,选B.
,选B.



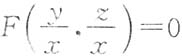 确定,其中F为可微函数,且F'2≠0,则
确定,其中F为可微函数,且F'2≠0,则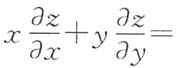
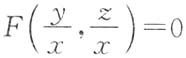 两端关于x求偏导,得
两端关于x求偏导,得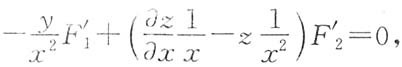 ①
①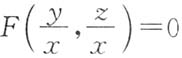 两端关于y求偏导,得
两端关于y求偏导,得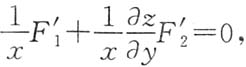 ②
②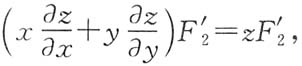
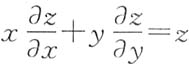 .即正确选项为B.
.即正确选项为B.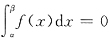 ,则
,则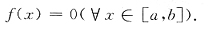
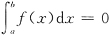 ,则f(x)=0(x∈[a,b]).
,则f(x)=0(x∈[a,b]).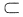 [a,b],则
[a,b],则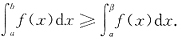

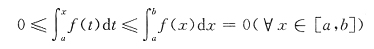
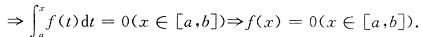

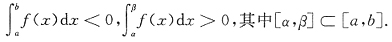
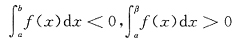 ,其中[α,β]
,其中[α,β]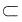 [a,b].
[a,b].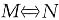 ”表示“M的充分必要条件是N”,则必有
”表示“M的充分必要条件是N”,则必有 f(x)是奇函数.
f(x)是奇函数. f(x)是偶函数.
f(x)是偶函数. f(x)是周期函数.
f(x)是周期函数. f(x)是单调函数.
f(x)是单调函数.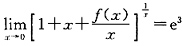 ,则
,则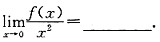
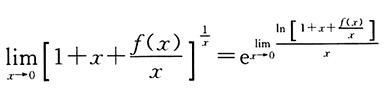 ,由题意得
,由题意得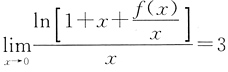 .
.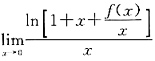 存在,
存在,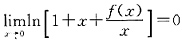 ,故当x→0时,
,故当x→0时,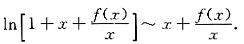
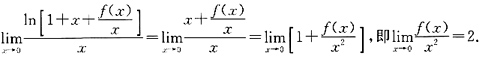
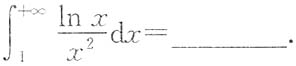
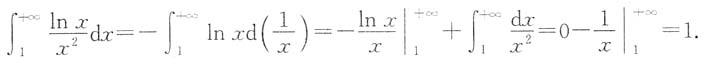

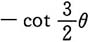
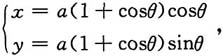 θ为参数.
θ为参数.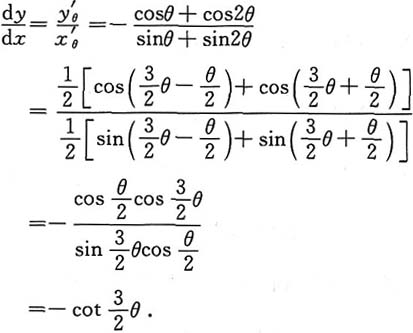
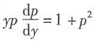 ,即
,即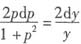 ,
,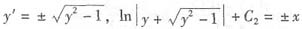 ,
,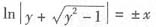 .
.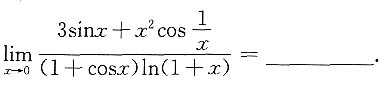
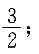
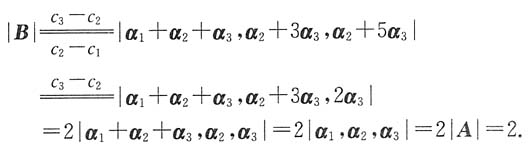
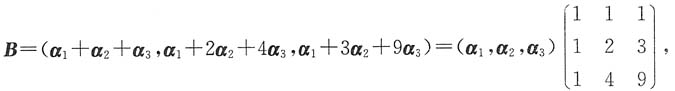

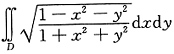 ,其中D={(x,y)|x2+y2≤1,x≥0,y≥0}.
,其中D={(x,y)|x2+y2≤1,x≥0,y≥0}.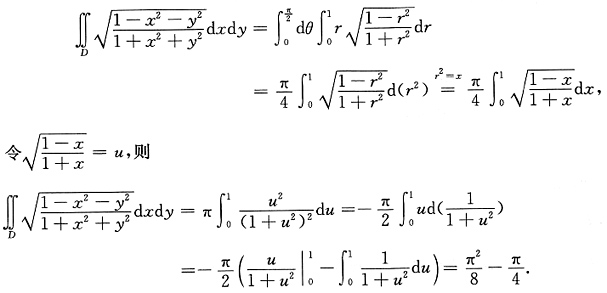
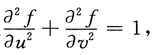 又
又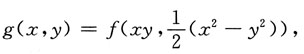 求
求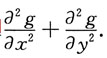

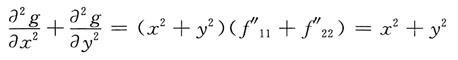
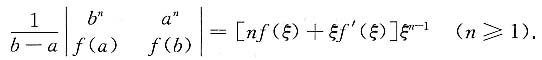
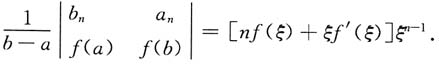
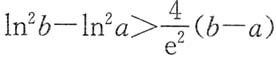 .
.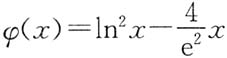 ,则
,则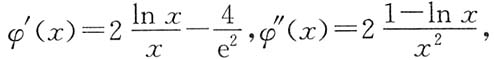
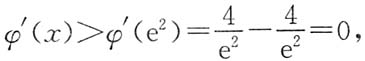
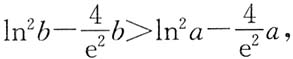
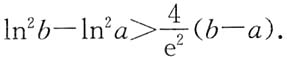
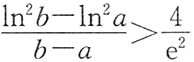 ,左端可看作函数f(x)=ln2x在[a,b]上的拉格朗日中值定理的形式,故
,左端可看作函数f(x)=ln2x在[a,b]上的拉格朗日中值定理的形式,故 ,a<ξ<b.下面对ξ作估计:
,a<ξ<b.下面对ξ作估计: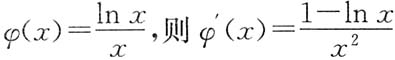 ,当x>e时,φ'(x)<0,则φ(x)在(e,+∞)上单调减少,故
,当x>e时,φ'(x)<0,则φ(x)在(e,+∞)上单调减少,故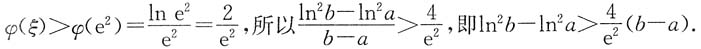
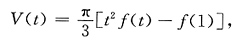
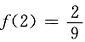 ,求函数y=f(x)的表达式.
,求函数y=f(x)的表达式.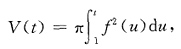
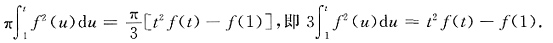
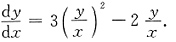
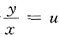 ,则有
,则有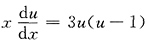 ,分离变量并两边积分得
,分离变量并两边积分得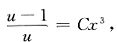 即y-x=Cx3y,
即y-x=Cx3y,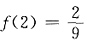 得C=-1,故
得C=-1,故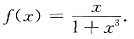
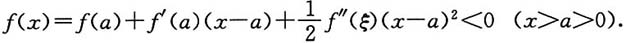
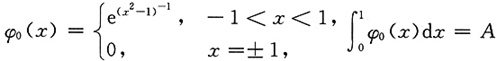 ,令
,令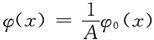 ,又有f(x)在[-1,1]上连续,若φn(x)=nφ(nx)(n=1,2,…),
,又有f(x)在[-1,1]上连续,若φn(x)=nφ(nx)(n=1,2,…),
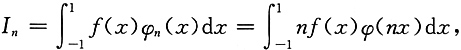
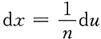 ,故
,故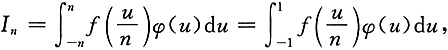
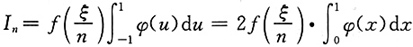
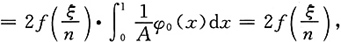
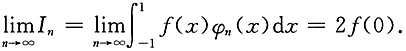
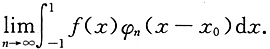
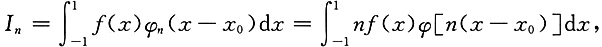
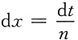 ,于是
,于是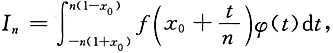
 [-n(1+x0),n(1-x0)],并应用积分中值定理,得到
[-n(1+x0),n(1-x0)],并应用积分中值定理,得到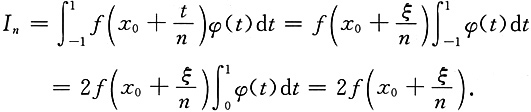
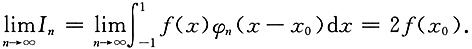
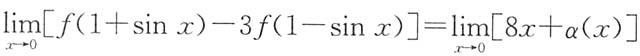 ,
,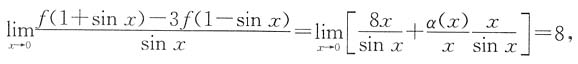
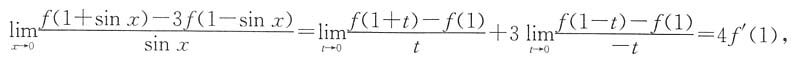
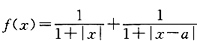 在(-∞,+∞)内的最值.
在(-∞,+∞)内的最值.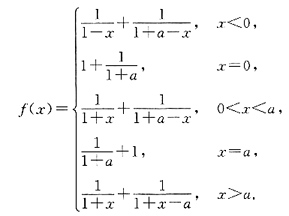
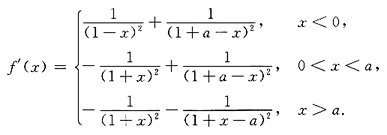
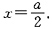
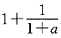 .
.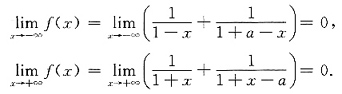
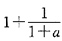 是f(x)在区间(-∞,+∞)内的最大值,f(x)在区间(-∞,+∞)内无最小值.
是f(x)在区间(-∞,+∞)内的最大值,f(x)在区间(-∞,+∞)内无最小值.