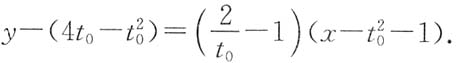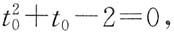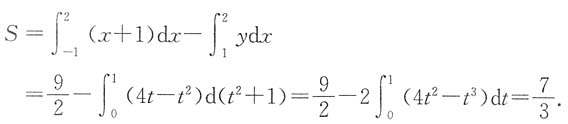一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的. 二、填空题1.
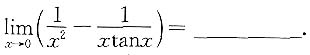
3. 设函数z=z(x,y)由方程2sin(x+2y-3z)=x+2y-3z确定,则
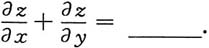
1
[解析] 令F(x,y,z)=x+2y-3z-2sin(x+2y-3z)=0,则
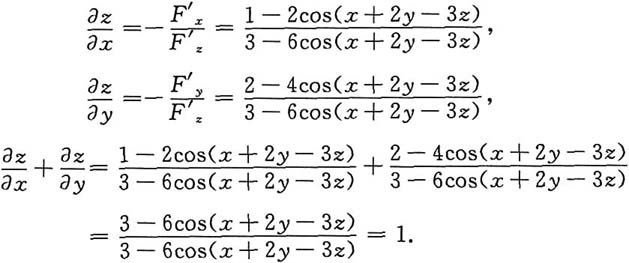
4. 函数f(x)=x
22
x在x=0处的n阶导数f
(n)(0)=______.
n(n-1)(ln2)n-2(n=1,2,3,…).
[解析] 解法1 用求函数乘积的n阶导数的莱布尼茨公式.
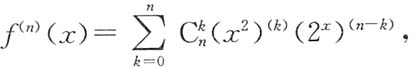
其中
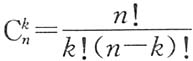
.注意(x
2)
(k)|
x=0=0(k≠2),
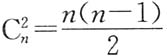
,于是

f'(0)=0,
因此f
(n)(0)=n(n-1)(ln2)
n-2(n=1,2,3,…).
解法2 利用泰勒展开
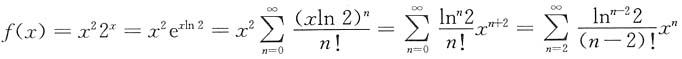
,由泰勒展开系数的唯一性,得
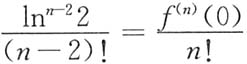
,故
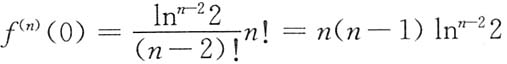
,n=2,3,….
5. 设
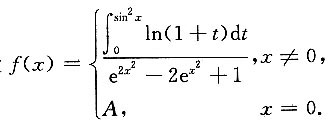
在x=0处连续,则A=______.
6.
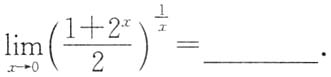
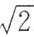
.
三、解答题本题共94分,解答应写出文字说明、证明过程或验算步骤.设n阶矩阵A满足A2+2A-3E=O.1. 证明矩阵A,A+2E,A+4E可逆,并求出它们的逆矩阵;
[解] 由
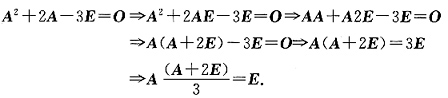
所以,矩阵A可逆,且
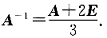
由于
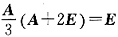
,所以矩阵A+2E可逆,且
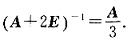
由于A
2+2A-3E=O,所以A
2+2A-8E=-5E.
而A
2+2A-8E=(A+4E)(A-2E),即(A+4E)(A-2E)=-5E.所以,矩阵A+4E可逆,且
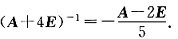
2. 当A≠E时,判断矩阵A+3E是否可逆,并说明理由.
[解] 当A≠E时,A-E≠O.
由于A2+2A-3E=O,因式分解得(A+3E)(A-E)=O.
令A-E=(α1,α2,…,αn),其中的每一列都是齐次线性方程组(A+3E)x=0的解,而A-E不是零矩阵,说明α1,α2,…,an中至少有一个向量不为0,即齐次线性方程组(A+3E)x=0有非零解.
故矩阵A+3E不是可逆矩阵,
3. 设函数
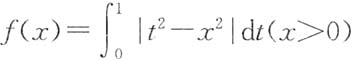
,求f'(x),并求f(x)的最小值.
解 当0<x≤1时,
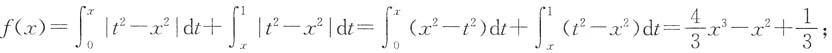
当x>1时,
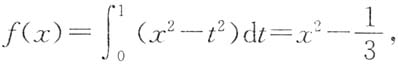
所以
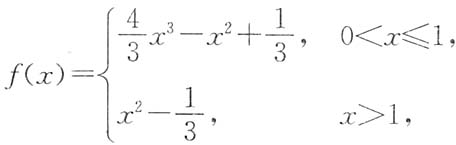
而

故
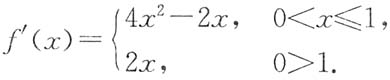
由f'(x)=0得唯一驻点
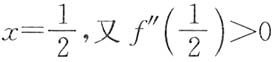
,从而
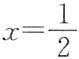
为f(x)的最小值点,最小值为
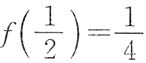
.
4. 设矩阵
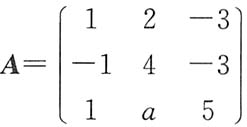
的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.
解 矩阵A的特征多项式为
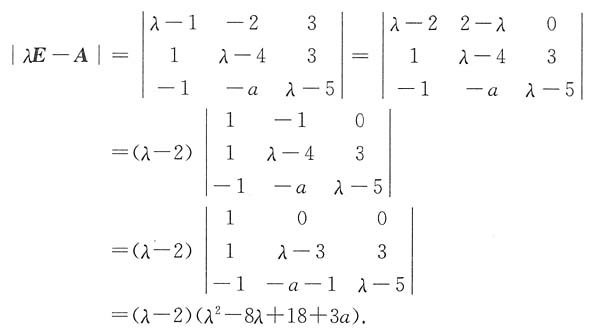
若λ=2是特征方程的二重根,则有2
2-16+18+3a=0,解得a=-2.
当a=-2时,A的特征值为2,2,6,矩阵
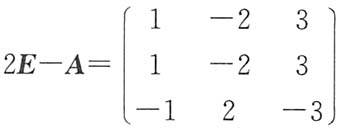
的秩为1,故λ=2对应的线性无关的特征向量有两个,从而A可相似对角化.
若λ=2不是特征方程的二重根,则λ
2-8λ+18+3a为完全平方,从而18+3a=16,解得

.
当
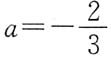
时,A的特征值为2,4,4,矩阵
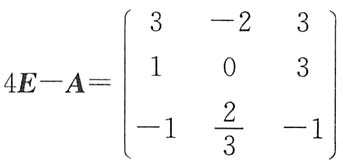
的秩为2,故λ=4对应的线性无关的特征向量只有一个,从而A不可相似对角化.
5. 设
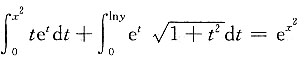
,求
.
6. 设φ(x)在区间[0,1]上具有二阶连续的导数,且φ(0)=φ(1)=0.证明
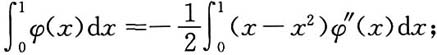
[证]由分部积分,
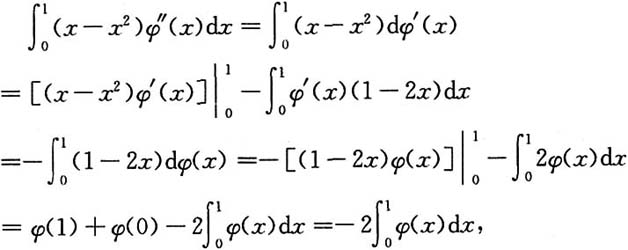
所以
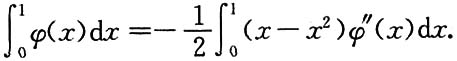
7. 设二元函数f(x,y)在区域D={(x,y)|0≤x≤1,0≤y≤1}上具有连续的4阶导数,且
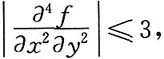
并设在D的边界上f(x,y)≡0.证明
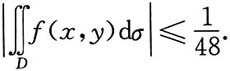
[证]
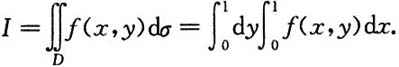
对于里层积分,y视为常数,对x积分,并注意到题设条件有
f(0,y)=f(1,y)=0.
所以套用上小题的结果,有
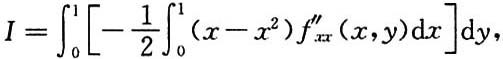
交换积分次序,得
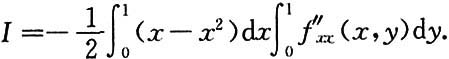
对此积分的里层积分,x视为常数,对y积分,并注意到条件
f(x,0)=f(x,1)=0.
再套用上小题的结果,有
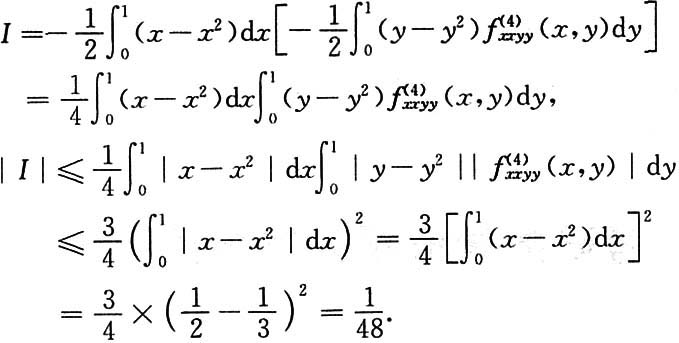
8. 在区间
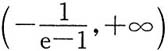
上设
f(x)=min{x,ln[1+(e-1)x]},
求∫f(x)dx,应写出详细的推导过程.
[解]令
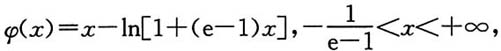
易见φ(0)=0,φ(1)=0.是否还有其他的x使φ(x)=0,为此考虑在区间
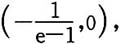
(0,1),(1,+∞)内φ(x)是否还会变号.
在区间
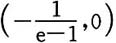
上,
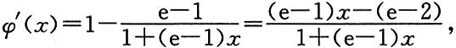
由于分母1+(e-1)x>0,分子(e-1)x-(e-2)<0,所以在区间
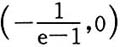
上,φ'(x)<0,又因φ(0)=0,所以在区间
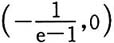
上,φ(x)>0.φ(x)在该区间内部无零点.
再考虑在区间(0,1)上,φ'(x)同上,仍有分母大于零.令φ'(x)的分子为零,得φ(x)的驻点
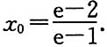
易见0<x
0<1.在区间(0,x
0)上,φ'(x)<0,又因φ(0)=0,所以在区间(0,x
0)上,φ(x)<0.在区间(x
0,1)上,φ'(x)>0,φ(1)=0,所以在区间(x
0,1)上,φ(x)<0.
再考虑在区间(1,+∞)上,仍有分母大于零,分子
1+(e-1)x-(e-1)=(e-1)(x-1)+1>0,
所以在区间(1,+∞)上φ'(x)>0.又因φ(1)=0,所以当x∈(1,+∞)时φ(x)>0.总结以上,有
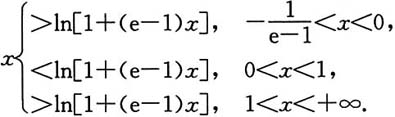
从而知
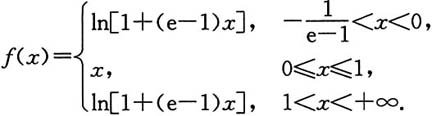
再考虑积分∫f(x)dx.由分部积分:
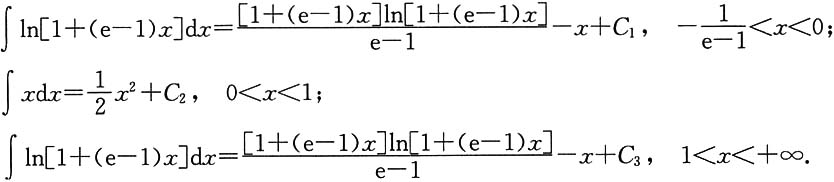
在交界点x=0与x=1处分别连续,于是有
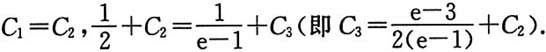
最后得
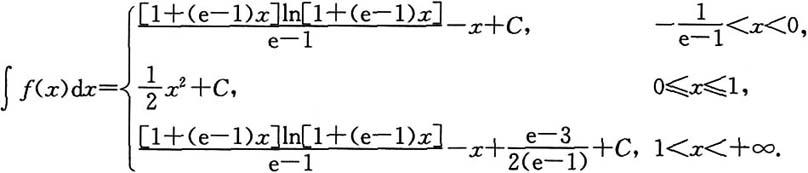
9. 确定常数a,使向量组α
1=(1,1,a)
T,α
2=(1,a,1)
T,α
3=(a,1,1)
T可由向量组β
1=(1,1,a)
T,β
2=(-2,a,4)
T,β
3=(-2,a,a)
T线性表示,但向量组β
1,β
2,β
3不能由向量组α
1,α
2,a
3线性表示.
解 记A=(α
1,α
2,a
3),B=(β
1,β
2,β
3).由于β
1,β
2,β
3不能由α
1,α
2,a
3线性表示,所以A的秩r(A)<3,从而行列式

得a=1或a=-2.
当a=1时,α
1=α
2=α
3=β
1=(1,1,1)
T,显然α
1,α
2,a
3可由β
1,β
2,β
3线性表示,而β
2=(-2,1,4)
T不能由α
1,α
2,a
3线性表示,即a=1符合题意.
当a=-2时,则有
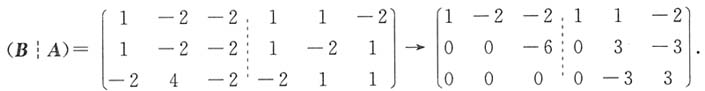
考虑非齐次线性方程组Bx=α
2,由上述可知矩阵B的秩r(B)=2,而秩
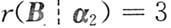
,则方程组Bx=α
2无解,即α
2不能由向量组β
1,β
2,β
3线性表示,所以a=-2不符合题意,应舍去.综上a=1.
[解析] 向量组α1,α2,a3可由向量组β1,β2,β3线性表示,则三个方程组xi1β1+xi2β2+xi3β3=αi(i=1,2,3)均有解;向量组β1,β2,β3不可由向量组α1,α2,a3线性表示,则三个方程组xi1α1+xi2α2+xi3α3=βi(i=1,2,3)至少一个无解.
10. 求微分方程
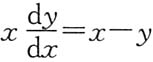
满足条件
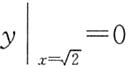
的特解.
解 化原方程为一阶线性方程
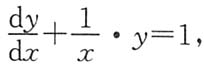
得其通解为
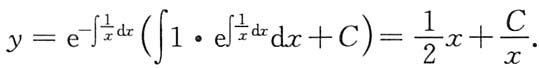
由
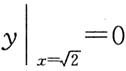
,得C=-1,故所求特解为
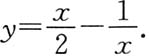
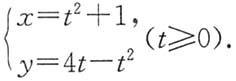
11. 讨论L的凹凸性;
解 由于
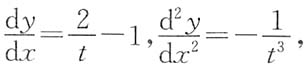
当t>0时,
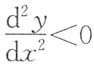
,故L是凸的.
12. 过点(-1,0)引L的切线,求切点(x
0,y
0),并写出切线的方程;
解 因为当t=0时,L在对应点处的切线方程为x=1,不合题意,故设切点(x
0,y
0)对应的参数为t
0>0,则L在(x
0,y
0)处的切线方程为
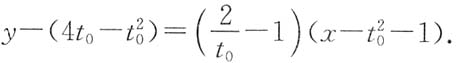
令x=-1,y=0.得
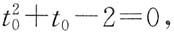
解得t
0=1或t
0=-2(舍去).
由t=1知,切点为(2,3),且切线方程为y=x+1.
13. 求此切线与L(对应于x≤x
0的部分)及x轴所围成的平面图形的面积.
解 由y=0时t=0,t=4知L与x轴的交点分别为(1,0)和(17,0).故所求平面图形的面积为
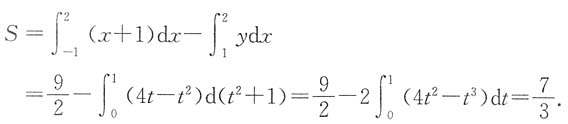
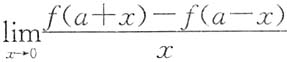 等于
等于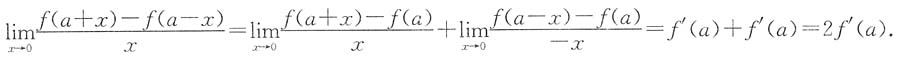
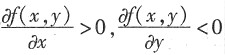 ,则______
,则______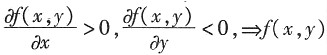 是关于y的单调递减函数,所以有f(0,1)<f(1,1)<f(1,0),故答案选D.
是关于y的单调递减函数,所以有f(0,1)<f(1,1)<f(1,0),故答案选D.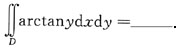
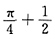
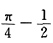
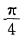
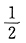
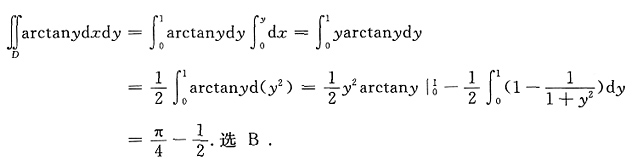
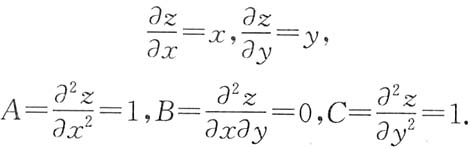
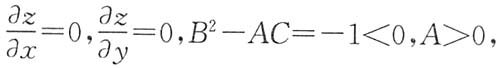
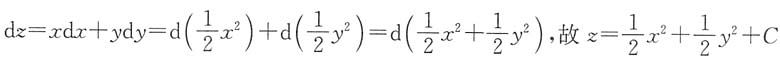 ,C是任意常数,由极值的定义可知,点(0,0)是极小值点.
,C是任意常数,由极值的定义可知,点(0,0)是极小值点.
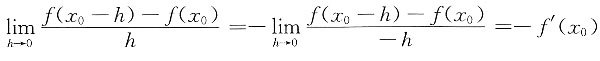 .选B.
.选B.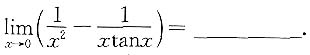
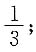
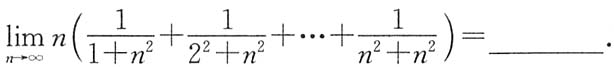
 .
.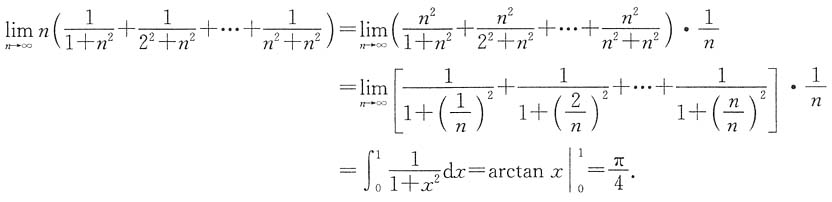
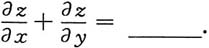
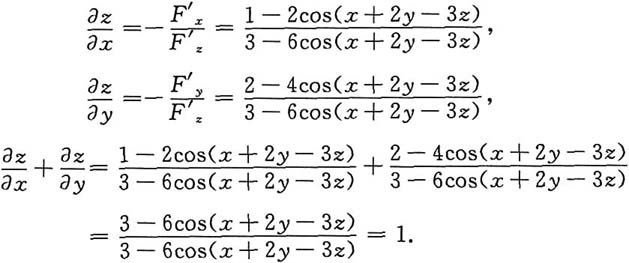
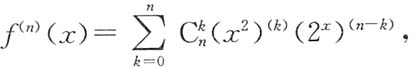
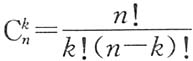 .注意(x2)(k)|x=0=0(k≠2),
.注意(x2)(k)|x=0=0(k≠2),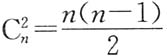 ,于是
,于是
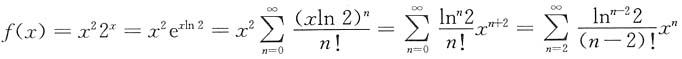 ,由泰勒展开系数的唯一性,得
,由泰勒展开系数的唯一性,得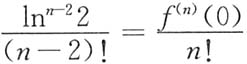 ,故
,故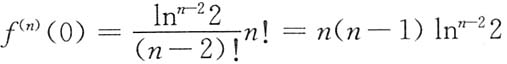 ,n=2,3,….
,n=2,3,….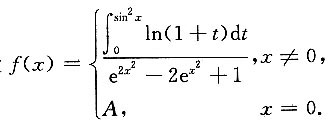 在x=0处连续,则A=______.
在x=0处连续,则A=______.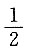
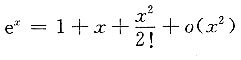 得
得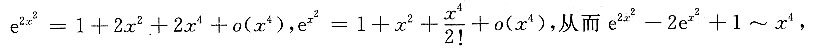
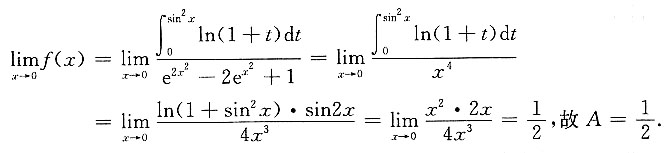
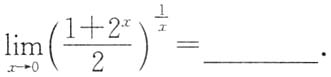
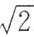 .
.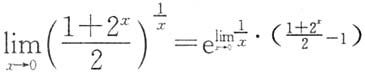 ,而
,而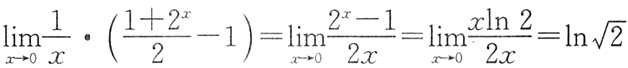 ,故
,故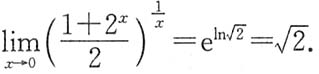
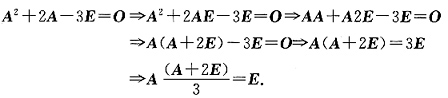
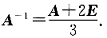
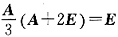 ,所以矩阵A+2E可逆,且
,所以矩阵A+2E可逆,且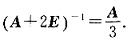
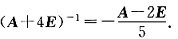
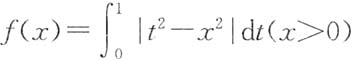 ,求f'(x),并求f(x)的最小值.
,求f'(x),并求f(x)的最小值.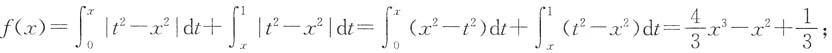
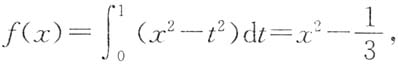
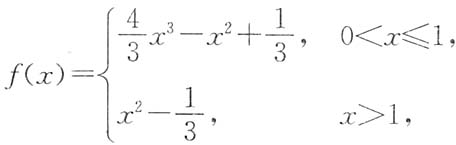

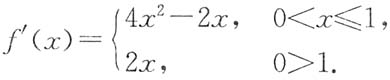
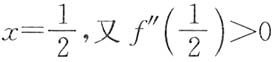 ,从而
,从而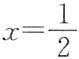 为f(x)的最小值点,最小值为
为f(x)的最小值点,最小值为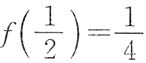 .
.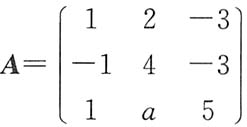 的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.
的特征方程有一个二重根,求a的值,并讨论A是否可相似对角化.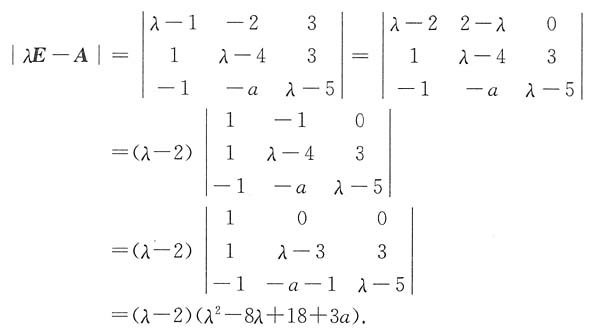
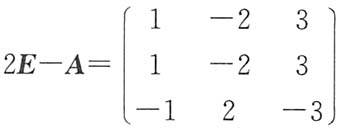 的秩为1,故λ=2对应的线性无关的特征向量有两个,从而A可相似对角化.
的秩为1,故λ=2对应的线性无关的特征向量有两个,从而A可相似对角化. .
.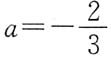 时,A的特征值为2,4,4,矩阵
时,A的特征值为2,4,4,矩阵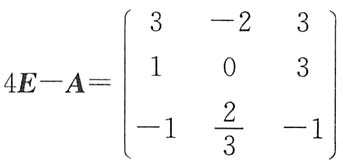 的秩为2,故λ=4对应的线性无关的特征向量只有一个,从而A不可相似对角化.
的秩为2,故λ=4对应的线性无关的特征向量只有一个,从而A不可相似对角化. ,求
,求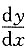 .
.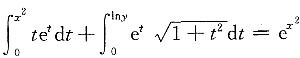 两边对x求导数得
两边对x求导数得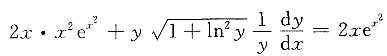 ,则
,则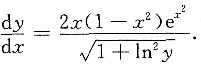
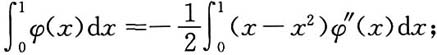
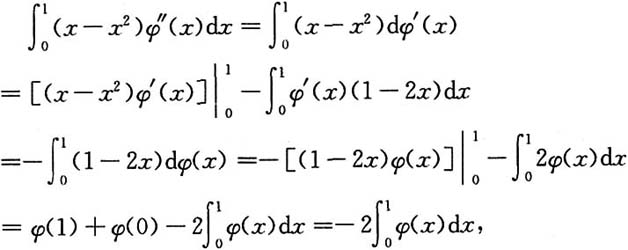
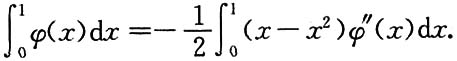
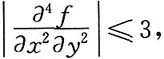 并设在D的边界上f(x,y)≡0.证明
并设在D的边界上f(x,y)≡0.证明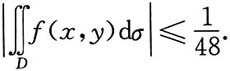
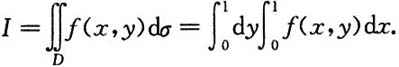
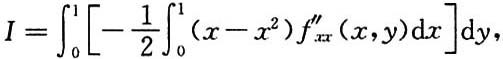
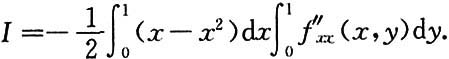
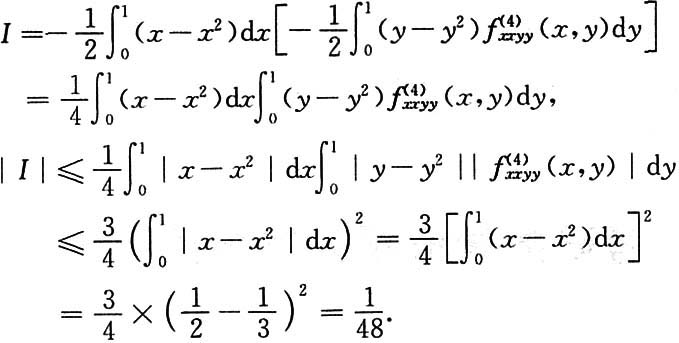
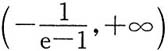 上设
上设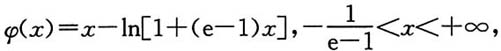
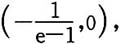 (0,1),(1,+∞)内φ(x)是否还会变号.
(0,1),(1,+∞)内φ(x)是否还会变号.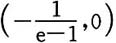 上,
上,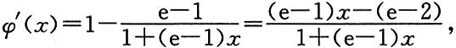
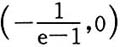 上,φ'(x)<0,又因φ(0)=0,所以在区间
上,φ'(x)<0,又因φ(0)=0,所以在区间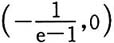 上,φ(x)>0.φ(x)在该区间内部无零点.
上,φ(x)>0.φ(x)在该区间内部无零点.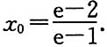
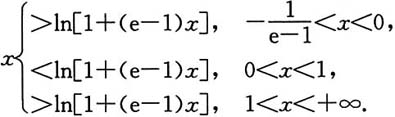
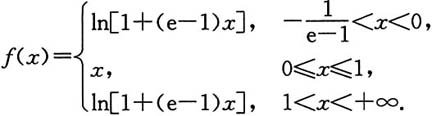
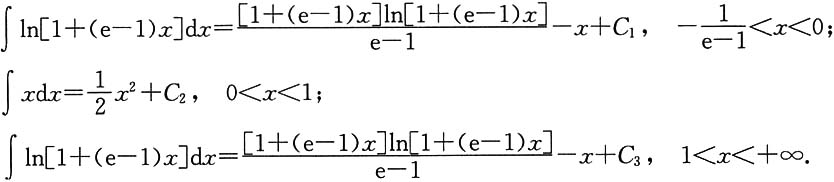
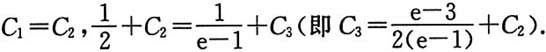
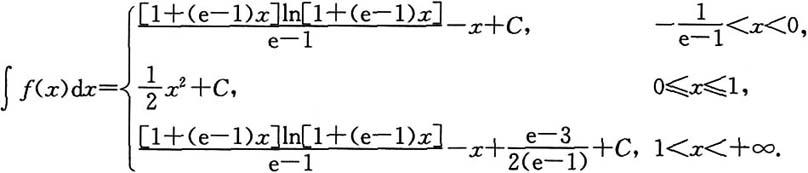

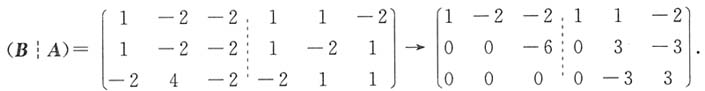
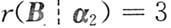 ,则方程组Bx=α2无解,即α2不能由向量组β1,β2,β3线性表示,所以a=-2不符合题意,应舍去.综上a=1.
,则方程组Bx=α2无解,即α2不能由向量组β1,β2,β3线性表示,所以a=-2不符合题意,应舍去.综上a=1.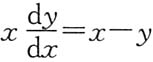 满足条件
满足条件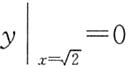 的特解.
的特解.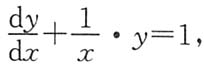 得其通解为
得其通解为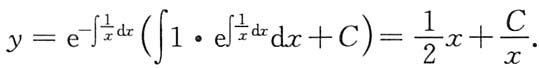
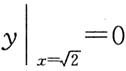 ,得C=-1,故所求特解为
,得C=-1,故所求特解为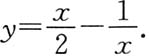
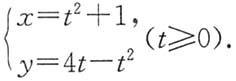
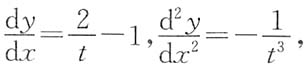
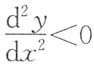 ,故L是凸的.
,故L是凸的.