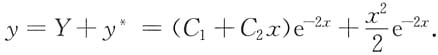一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设
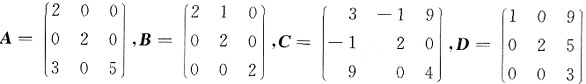
,那么与对角矩阵相似的矩阵是______
- A.A,B,C.
- B.A,C,D.
- C.B,D.
- D.A,C.
A B C D
B
[解析] 矩阵C为实对称矩阵,一定可以与对角矩阵相似.矩阵D有3个不同的特征值,一定可以与对角矩阵相似,矩阵B有3个相同的特征值,且B不是对角矩阵,一定不能与对角矩阵相似,反证即可.事实上,若存在可逆矩阵P,使
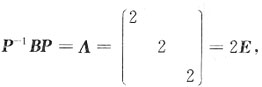
于是
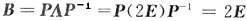
,矛盾.
至于矩阵A,其特征值λ
1=λ
2=
2,λ
3=5(单,重,重).
当λ=λ
1=λ
2=2时,由(A-2E)x=0,
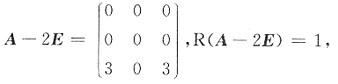
于是与λ
1=λ
2=2对应的有2个线性无关的特征向量,因此A可以与对角矩阵相似.
选B.
2. 下列矩阵中不能相似于对角阵的矩阵是
A.
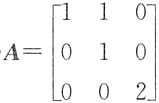
B.
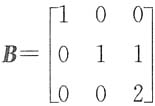
C.
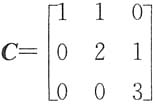
D.
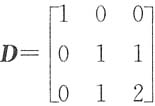
A B C D
A
[解析] 因(D)是对称阵,必相似于对角阵,(C)有三个不同的特征值,能相似于对角阵.(A),(B)的特征值均为λ=1(2重),λ=2(单根).当λ=1时,
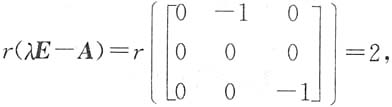
只对应一个线性无关的特征向量。故A不能相似于对角阵.
而λ=1时,
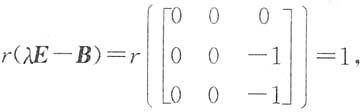
有两个线性无关特征向量,故B能相似于对角阵,故选(A).
4. 设
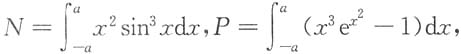
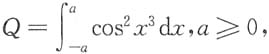
则______
- A.N≤P≤Q
- B.N≤Q≤P
- C.Q≤P≤N
- D.P≤N≤Q
A B C D
D
[解析] x
2sin
3x是奇函数,故N=0,x
3e
x2是奇函数,故
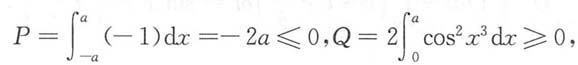
所以P≤N≤Q.
5. 设P(A)=0.5,P(B)=0.6,则P(A∪B)-P(A∩B)的取值范围为______
- A.[0.1,1].
- B.[0,0.9].
- C.[0.1,0.9].
- D.[0,1].
A B C D
C
[解析] 由P(A∩B)≤min{P(A),P(B)}=0.5,当
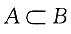
时,P(A∩B)取得最大值0.5.
由P(A∪B)=P(A)+P(B)-P(A∩B)≤1,得
P(A∩B)≥P(A)+P(B)-1=0.1.
又由
P(A∪B)-P(A∩B)=P(A)+P(B)-2P(A∩B)=1.1-2P(A∩B),
故当P(A∩B)取最大值0.5,P(A∪B)-P(A∩B)最小为0.1,当P(A∩B)取最小值0.1,P(A∪B)-P(A∩B)最大为0.9.选C.
8. 设随机向量(X,Y)的概率密度f(x,y)满足f(x,y)=f(-x,y),且ρ
XY存在,则ρ
XY=______
A B C D
B
[解析]
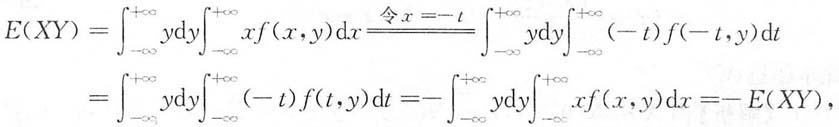
所以E(XY)=0.
同理,
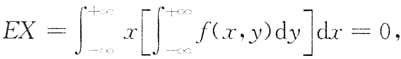
所以ρ
XY=0.
同理,当f(x,y)=f(x,-y)时,ρ
XY=0.
二、填空题1. f(x)=
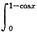
sint
2dt,当x→0时,f(x)是x的n阶无穷小,则n=______.
6
[解析] 可用下述结论观察求出,也可利用n阶无穷小定义求出.
当f(x)连续且x→a时,f(x)是x→a的n阶无穷小量,g(x)是x-a的m阶无穷小量,则当x→a时,
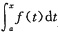
必为x-a的n+1阶无穷小量,
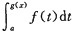
必为x-a的(n+1)m阶无穷小量.
解一 因sinx
2是x-0=x的2阶无穷小量,1-cosx~x
2/2为x的2阶无穷小量,则x→0时,
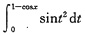
为x的(2+1)×2=6阶无穷小量,即n=6.
解二

因而n=6.
3. 数列

的最小项的项数n=______,且该项的数值为______.
5;
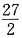
[解析] 设
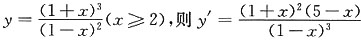
,令y'=0,在所考虑的定义域内有唯一解x=5,当2<x<5时,y'<0,当x>5时,y'>0,故函数y在x=5处取极小值,也是最小值,最小值
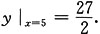
本题考查的知识点是(函数)数列极值的求解.
4. 已知β=(0,2,-1,a)
T可以由α
1=(1,-2,3,+4)
T,α
2=(0,1,-1,1)
T,α
3=(1,3,a,1)
T线性表出,则a=______.
2
[解析] 设x
1α
1+x
2α
2+x
3α
3=β,对(α
1,α
2,α
3
β)作初等行变换,有
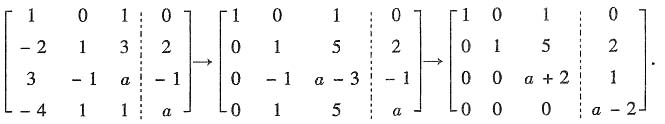
当a≠2时r(α
1,α
2,α
3)≠r(α
1,α
2,α
3
β),β不能由α
1,α
2,α
3线性表出,故a=2.
5. 已知X
1,X
2…,X
n为取自分布为F(x)的总体X的简单随机样本.记X=min(X
1,…,X
n-1)和Y=X
n则X的分布函数F
X(x)=______,Y的分布函数F
Y(y)=______和(X,Y)的联合分布G(x,y)=______.
1-[1-F(x)]n-1;F(y);{1-[1-F(x)]n-1}F(y)
[解析] 根据简单随机样本各分量Xi相互独立且与X同分布,有
Fx(x)=P{min(X1,X2…,Xn-1)≤x}=1-P{min(X1,X2…,Xn-1)>x}
=1-P{X1>x,X2>x,…,Xn-1>x}=1-P{X1>x}P{X2>x}…P{Xn-1>x}
=1-[1-P{X1≤x}][1-P{X2≤x}]…[1-P{Xn-1≤x}]=1-[1-F(x)]n-1.
FY(y)=P{Xn≤y}=F(y)
G(x,y)=P{min(X1,…,Xn-1)≤x,Xn≤y}=P{min(X1,…,Xn-1)≤x}P{Xn≤y}
={1-[1-F(x)]n-1}F(y).
三、解答题共94分,解答应写出文字说明、证明过程或验算步骤.1. 设随机变量X~N(μ,σ
2),Y~U[-π,π],且X,Y相互独立,令Z=X+Y,求f
Z(z).
解:因为X~N(μ,σ
2),Y~U[-π,π],所以X,Y的密度函数为
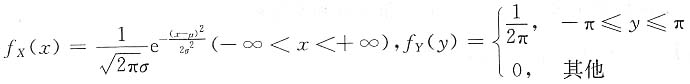
又X,Y相互独立,所以X,Y的联合密度函数为
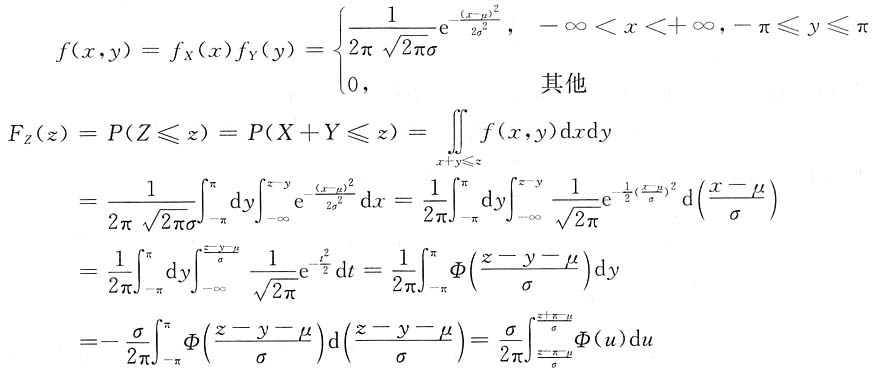
则
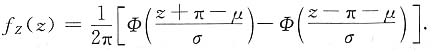
2. 设

有极限值l,试求a及l的值.
解:由于X→-1时,分母趋于零,这样,为使其存在极限,分子必须也趋于零,即此式为
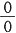
型未定式.
注意到,为使分子为无穷小量,必须(-1)
3-a+1+4=0,即a=4.
将a=4代入原极限式,再使用洛必达法则,就有

即l=10.
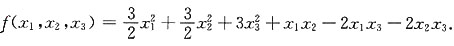
3. 用正交变换化二次型为标准形,并写出所作的正交变换及标准形;
解:
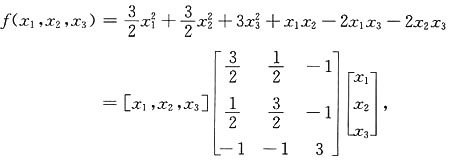
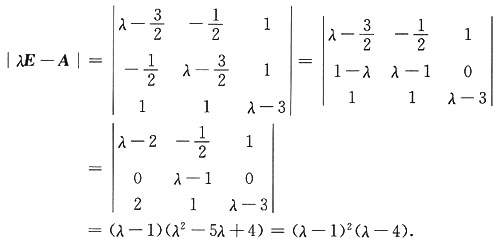
得λ
1=λ
2=1,λ
3=4,
λ
1=1时,
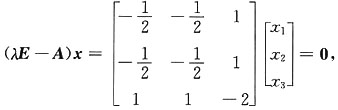
得ξ
1=[1,1,1],ξ
2=[1,-1,0].
(取ξ
2时,考虑到既满足方程,是λ=1对应的特征向量,又和ξ
1正交)

得ξ
3=[1,1,-2],将ξ
1,ξ
2,ξ
3单位化,并合并成正交阵,得
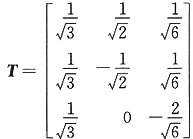
令x=Ty,则
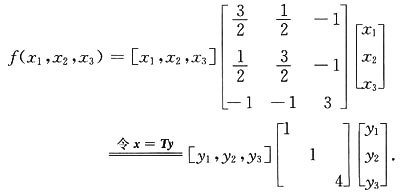
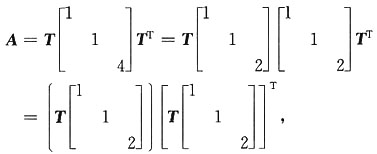
4. 是否存在可逆阵W,使得WW
T=A.其中A是二次型的对应矩阵,若存在,求W,若不存在,说明理由.
5. 总体X的概率密度为
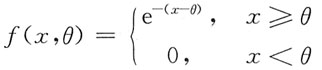
(θ>0未知),X
1,X
2,…,X
n为来自总体X的简单随机样本,试求参数θ的最大似然估计量,并讨论是否为无偏估计量.
解:取一组样本值x
1,x
2,…,x
n,均大于等于θ,于是有似然函数
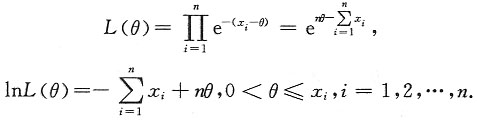
显然,当θ取可能的最大值时,L(θ)为最大.
而θ取值范围是0<θ≤min{x
1,x
2,…,x
n},故当θ=min{x
1,x
2,…,x
n}时,L(θ)的最大.
因此,θ的最大似然估计为
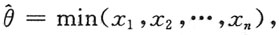
即最大似然估计量为
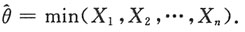
由于
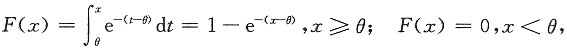
所以
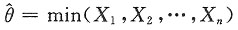
的分布函数为
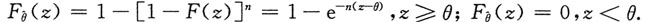
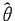
的分布为密度为

所以
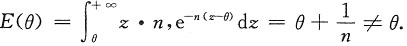
所以
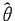
不是θ的无偏估计量.
6. 求(y
3-3xy
2-3x
2y)dx+(3xy
2-3x
2y-x
3+y
2)dy=0的通解.
解:将原给方程通过视察分项组合.
(y
3-3xy
2-3x
2y)dx+(3xy
2-3x
2y-x
3+y
2)dy
=(y
3dx+3xy
3dy)-3xy(ydx+xdy)-(3x
3ydx+x
3dy)+y
2dy
=0,
即
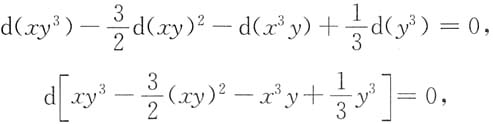
所以通解为
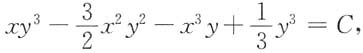
其中C为任意常数.
7. 设A是m×n矩阵,证明:存在非零的n×s矩阵B,使得AB=O的充要条件是r(A)<n.
证明:充分性 r(A)<n,AX=0有非零解,将非零解X组成B,则B≠O,且有AB=O.
必要性 若AB=O,其中B≠O,设B=[β1,β2,…,βs],则Aβi=0,i=1,2,…,s.其中βi,i=1,2,…,s,不全为0,即AX=0有非零解,故r(A)<n.
8. 早晨开始下雪整天不停,中午一扫雪车开始扫雪,每小时扫雪体积为常数,到下午2点扫雪2km,到下午4点又扫雪1km,问降雪是什么时候开始的?
解:设单位面积在单位时间内降雪量为a,路宽为b,扫雪速度为c,路面上雪层厚度为H(t),扫雪车前进路程为S(t),降雪开始时间为T,则
H(t)=a(t-T),又b×H(t)×Δs=c×Δt,
于是
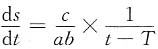
,令
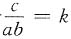
,则
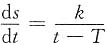
,且S(12)=0,S(14)=2,S(16)=3,
由
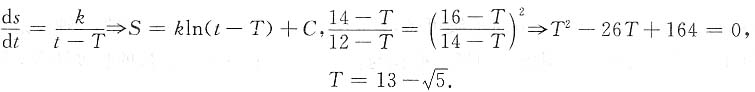
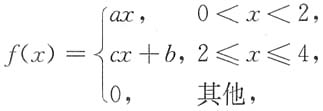 已知EX=2,
已知EX=2,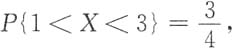 求
求10. 随机变量Y=e
X的数学期望和方差.
解:
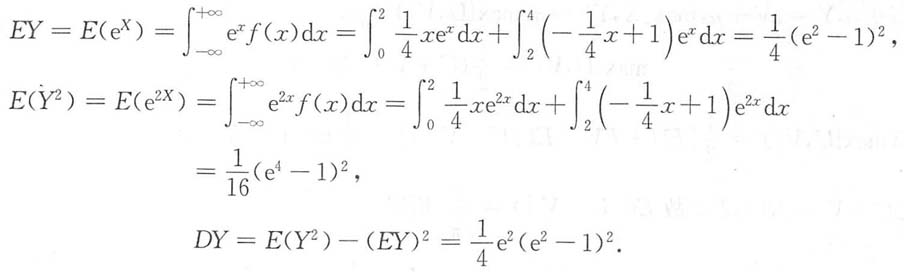
11. 求微分方程y"+4y'+4y=e
-2x的通解.
解:特征方程r
2+4r+4=0的根为r
1=r
2=-2.对应齐次方程的通解为
Y=(C
1+C
2x)e
-2x.
设原方程的特解y
*=Ax
2e
-2x,代入原方程得
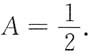
因此,原方程的通解为
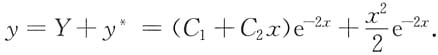
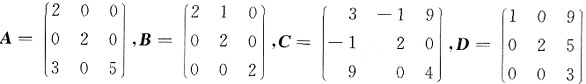 ,那么与对角矩阵相似的矩阵是______
,那么与对角矩阵相似的矩阵是______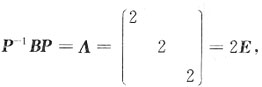 于是
于是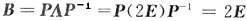 ,矛盾.
,矛盾.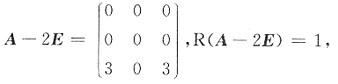
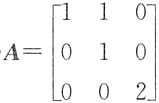
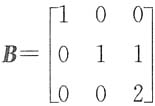
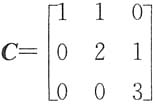
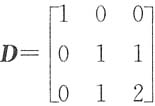
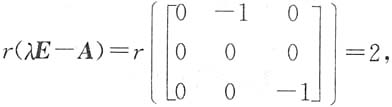 只对应一个线性无关的特征向量。故A不能相似于对角阵.
只对应一个线性无关的特征向量。故A不能相似于对角阵.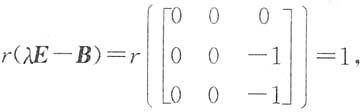 有两个线性无关特征向量,故B能相似于对角阵,故选(A).
有两个线性无关特征向量,故B能相似于对角阵,故选(A).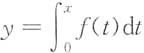
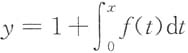
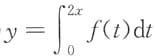
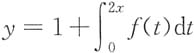
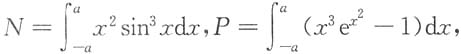
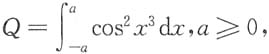 则______
则______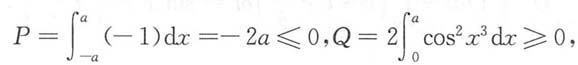
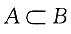 时,P(A∩B)取得最大值0.5.
时,P(A∩B)取得最大值0.5.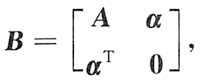 已知r(A)=r(B),则线性方程组______
已知r(A)=r(B),则线性方程组______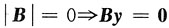 必有非零解.
必有非零解.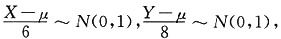 可见,
可见,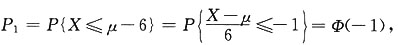
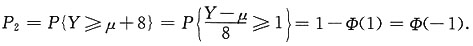
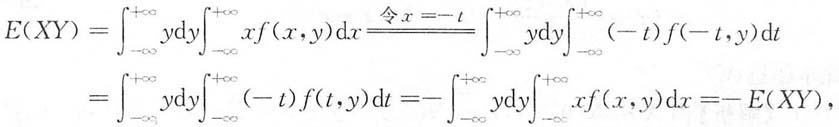
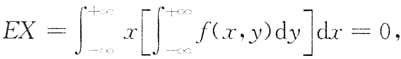 所以ρXY=0.
所以ρXY=0.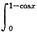 sint2dt,当x→0时,f(x)是x的n阶无穷小,则n=______.
sint2dt,当x→0时,f(x)是x的n阶无穷小,则n=______.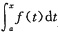 必为x-a的n+1阶无穷小量,
必为x-a的n+1阶无穷小量,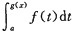 必为x-a的(n+1)m阶无穷小量.
必为x-a的(n+1)m阶无穷小量.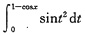 为x的(2+1)×2=6阶无穷小量,即n=6.
为x的(2+1)×2=6阶无穷小量,即n=6.
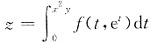 ,f有一阶连续的偏导数,则
,f有一阶连续的偏导数,则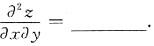
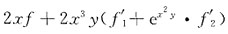
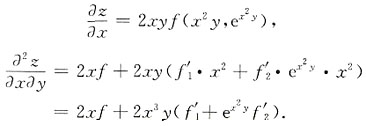
 的最小项的项数n=______,且该项的数值为______.
的最小项的项数n=______,且该项的数值为______.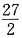
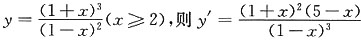 ,令y'=0,在所考虑的定义域内有唯一解x=5,当2<x<5时,y'<0,当x>5时,y'>0,故函数y在x=5处取极小值,也是最小值,最小值
,令y'=0,在所考虑的定义域内有唯一解x=5,当2<x<5时,y'<0,当x>5时,y'>0,故函数y在x=5处取极小值,也是最小值,最小值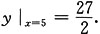
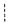 β)作初等行变换,有
β)作初等行变换,有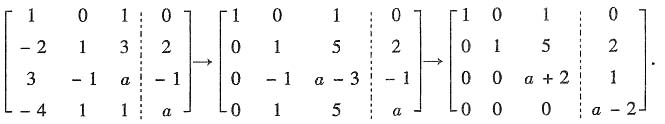
 β),β不能由α1,α2,α3线性表出,故a=2.
β),β不能由α1,α2,α3线性表出,故a=2.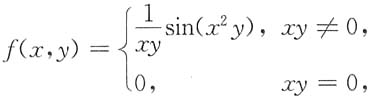 则
则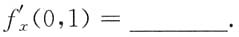
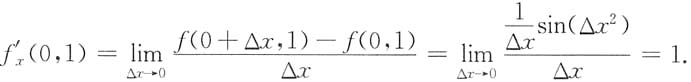
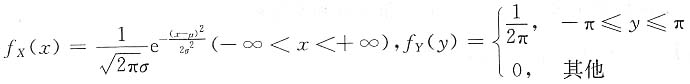
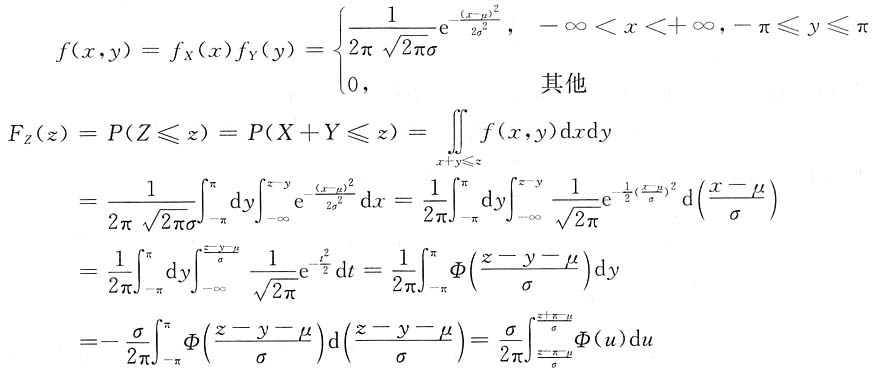
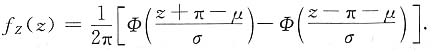
 有极限值l,试求a及l的值.
有极限值l,试求a及l的值.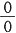 型未定式.
型未定式.
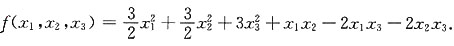
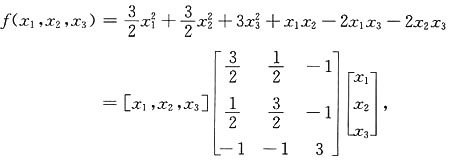
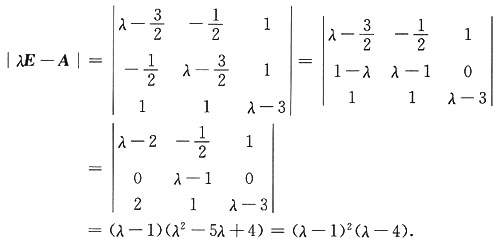
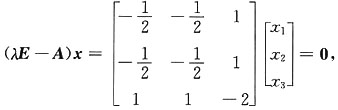

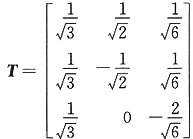
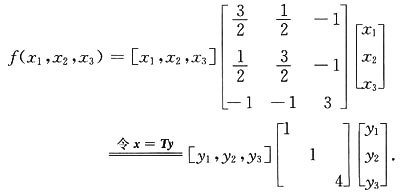
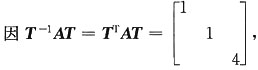
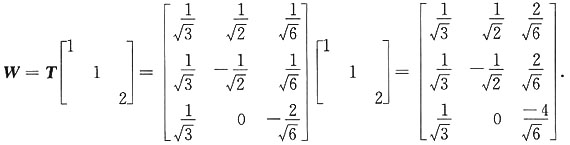
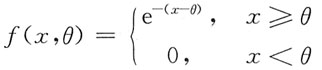 (θ>0未知),X1,X2,…,Xn为来自总体X的简单随机样本,试求参数θ的最大似然估计量,并讨论是否为无偏估计量.
(θ>0未知),X1,X2,…,Xn为来自总体X的简单随机样本,试求参数θ的最大似然估计量,并讨论是否为无偏估计量.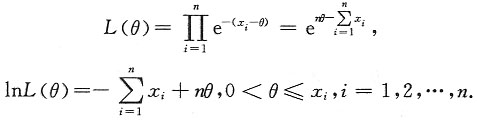
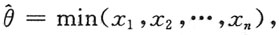
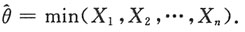
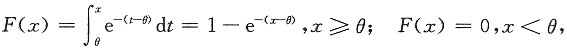
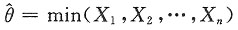 的分布函数为
的分布函数为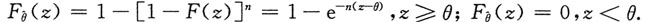
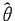 的分布为密度为
的分布为密度为
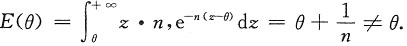
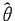 不是θ的无偏估计量.
不是θ的无偏估计量.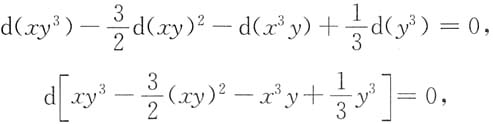
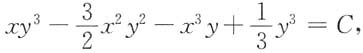 其中C为任意常数.
其中C为任意常数.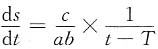 ,令
,令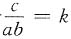 ,则
,则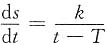 ,且S(12)=0,S(14)=2,S(16)=3,
,且S(12)=0,S(14)=2,S(16)=3,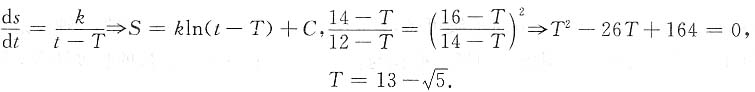
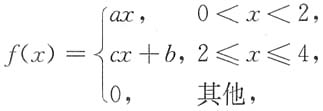 已知EX=2,
已知EX=2,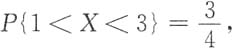 求
求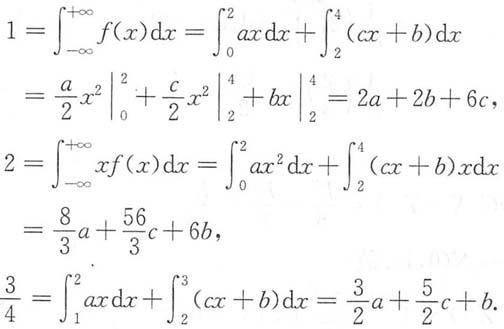
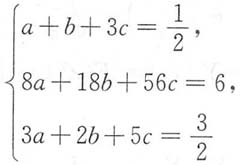
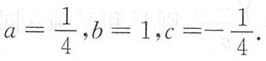
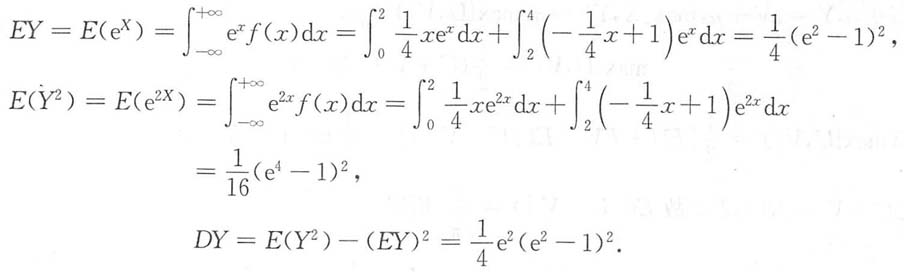
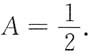 因此,原方程的通解为
因此,原方程的通解为