一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.2. 设λ
1,λ
2是n阶矩阵A的特征值,α
1,α
2分别是A的对应于λ
1,λ
2的特征向量,则______
- A.当λ1=λ2时,α1,α2对应分量必成比例
- B.当λ1=λ2时,α1,α2对应分量不成比例
- C.当λ1≠λ2时,α1,α2对应分量必成比例
- D.当λ1≠λ2时,α1,α2对应分量必不成比例
A B C D
D
[解析] 当λ1=λ2时,α1与α2可以线性相关也可以线性无关,所以α1,α2可以对应分量成比例,也可以对应分量不成比例,故排除(A),(B).当λ1≠λ2时,α1,α2一定线性无关,对应分量一定不成比例,故选(D).
4. 设a为常数,
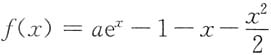
,则f(x)在区间(-∞,+∞)内______
- A.当a>0时f(x)无零点,当a≤0时f(x)恰有一个零点
- B.当a>0时f(x)恰有两个零点,当a≤0时f(x)无零点
- C.当a>0时f(x)恰有两个零点,当a≤0时f(x)恰有一个零点
- D.当a>0时f(x)恰有一个零点,当a≤0时f(x)无零点
A B C D
D
[解析] 本题考查一元微分学的应用,讨论函数的零点问题.
令
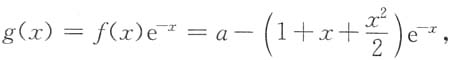
由于e
-x>0,g(x)与f(x)的零点完全一样,又
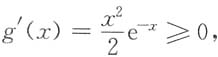
且仅在一点x=0等号成立,故g(x)严格单调增,所以g(x)至多有一个零点,从而f(x)至多有一个零点.
当a>0时,f(-∞)<0,f(+∞)>0,由连续函数零点定理,f(x)至少有一个零点,至少、至多合在一起,所以f(x)正好有一个零点.
当a≤0,
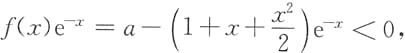
f(x)无零点.
6. 设矩阵A=(α
1,α
2,α
3,α
4)经行初等变换为矩阵B=(β
1,β
2,β
3,β
4),且α
1,α
2,α
3线性无关,α
1,α
2,α
3,α
4线性相关。则______.
- A.β4不能由β1,β2,β3线性表示
- B.β4能由β1,β2,β3线性表示,但表示法不唯一
- C.β4能由β1,β2,β3线性表示,且表示法唯一
- D.β4能否由β1,β2,β3线性表示不能确定
A B C D
C
[解析] 因为α1,α2,α3线性无关,而α1,α2,α3,α4线性相关,所以α4可由α1,α2,α3唯一线性表示,又A=(α1,α2,α3,α4)经过有限次初等行变换化为B=β1,β2,β3,β4),所以方程组x1α1+x2α2+x3α3=α4与x1β1+x2β2+x3β3=β4是同解方程组,因为方程组x1α1+x2α2+x3α3=α1有唯一解,所以方程组x1β1+x2β2+x3β3=β4有唯一解.即β4可由β1,β2,β3
唯一线性表示,选C.
8. 设
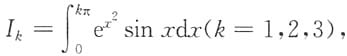
则有______
- A.I1<I2<I3
- B.I3<I2<I1
- C.I2<I3<I1
- D.I2<I1<I3
A B C D
D
[解析] 首先,由
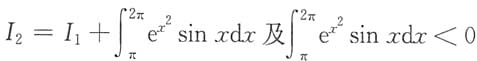
可得,I
2<I
1.
其次,
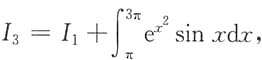
其中
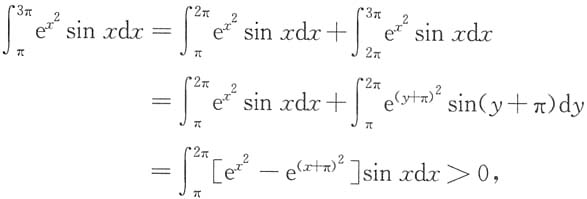
故I
3>I
1,从而I
2<I
1<I
3,故选(D).
二、填空题1. 设A,B,C是两两独立且不能同时发生的随机事件,且P(A)=P(B)=P(C)=P,则P的最大值为______.
[解析] 由题设
P(AB)=P(AC)=P(BC)=P
2,P(ABC)=0,
于是
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
=3P-3P
2,
而
P(A+B+C)≥P(A+B)=P(A)+P(B)-P(AB)=2P-P
2,
即有 3P-3P
2≥2P-P
2,
即P(1-2P)≥0,解得
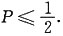
2. 已知α,β为常数,f(x)可导,则
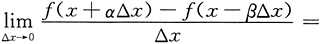
______.
(α+β)f'(x)
[解析]
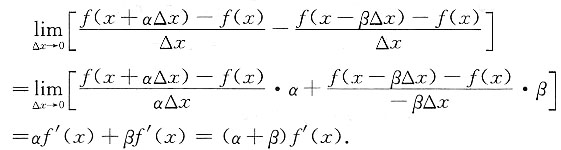
3. 设f(x)为连续函数,且
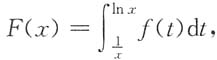
则F'(x)=______.
[解析] 由变限积分求导公式
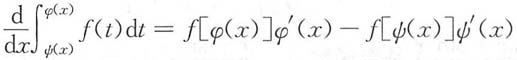
可知,
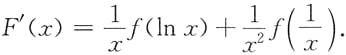
4. 设随机变量X的概率分布为
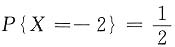
,P{X=1}=a,P{X=3}=b,若E(X)=0,则D(X)=______.
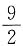
.
[解析] 根据分布律的归一性可知,
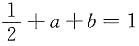
,又EX=0,则
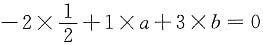
,即a+3b=1.联立方程
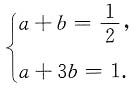
解得
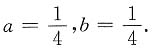
从而

6. 设D={(x,y)|1≤x
2+y
2≤e
2},则二重积分
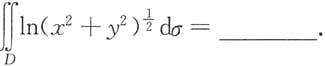
[解析] 被积函数的特点含有x
2+y
2的形式,且积分域是以原点为中心的圆环域,选用极坐标计算较方便.
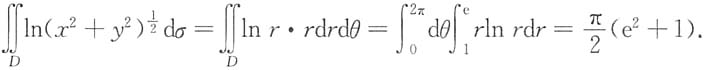
三、解答题共94分,解答应写出文字说明、证明过程或验算步骤.1. 计算
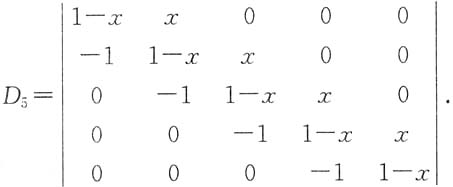
解:按第一行展开
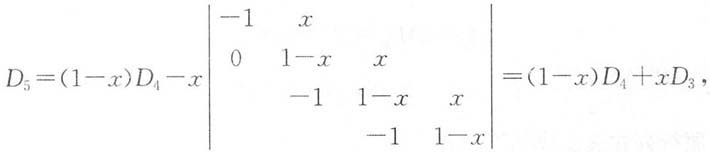
得到递推公式
D
5-D
4=-x(D
4-D
3)=…=-x
3(D
2-D
1).
由于
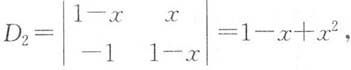
D
1=1-x,于是得
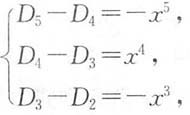
容易推出D
5=-x
5+x
4-x
3+D
2=-x
5+x
4-x
3+x
2-x+1.
2. 求函数
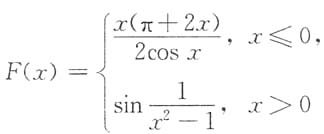
的间断点,并判断它们的类型.
解:对于函数F(x)的分段点x=0,因
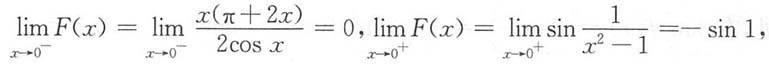
故x=0是函数F(x)的跳跃间断点.
当x>0时,
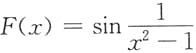
在x=1处没有定义,且极限
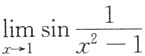
不存在.故x=1是函数F(x)的振荡间断点.
当x<0时,
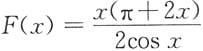
在点列
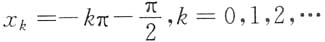
处没有定义,则这些点都是函数F(x)的间断点.特别对点
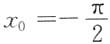
,令
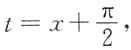
有
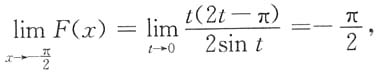
故
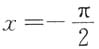
是函数F(x)的可去间断点;而点列
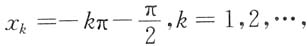
显然是函数F(x)的无穷间断点.
3. 设A是n阶实矩阵,证明:tr(AA
T)=0的充分必要条件是A=O.
解:充分性A=O,显然tr(AA
T)=0.
必要性tr(AA
T)=0,设

记B=AA
T,则
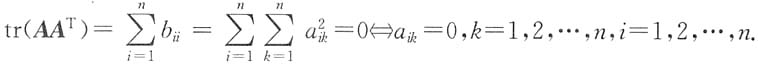
即A=O.
4. 求极限
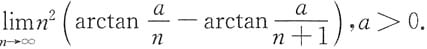
解:方法一 原极限等价于求
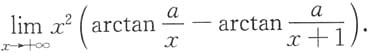
令f(t)=arctant,
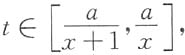
由拉格朗日中值定理可得
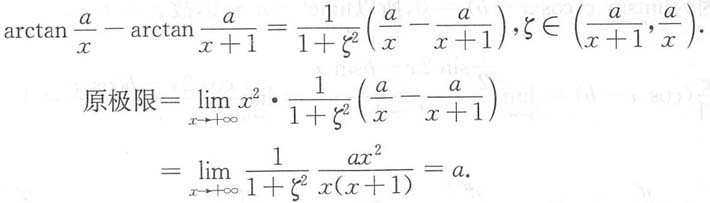
方法二

令
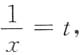
则
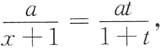
所以
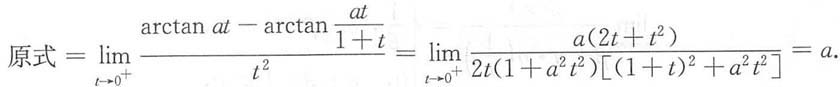
5. 若|f(x)|≤1(x∈[-2,2]),又
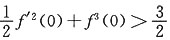
,证明:
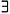
x
0∈(-2,2),使得f"(x
0)+3f
2(x
0)=0.
证明:令
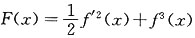
,要证
x
0∈(-2,2),F'(x
0)=0,f'(x
0)≠0,我们用前面分析中指出的方法(3)来证明.
由中值定理,
α∈(-2,0),使得

同理,
β∈[0,2]使得
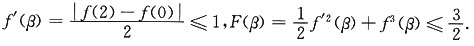
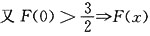
在[α,β]上的最大值必在(α,β)中某点x
0取到,于是F"(x
0)=0,即f'(x
0)(f"(x
0)+3f
2(x
0))=0.
知f'(x
0)≠0,否则.
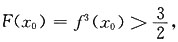
与|f(x)|≤1矛盾.
因此f"(x
0)+3f
2(x
0)=0.
6. 若f'(x)>0(x∈(-2,2)),又
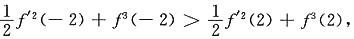
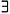
a∈(-2,2)使得f"(a)≥0,证明:
x
0∈(-2,2)使得f"(x
0)+3f
2(x
0)=0.
证明:令
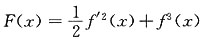
,要证
x
0∈(-2,2),使得F'(x
0)=0.我们用分析中提到的方法(2)证明.
按假设条件:F'(α)=f'(α)[f"(α)+3f
2(α)]≥0.
若等号成立,则命题得证.若F'(α)>0,则必
β∈(-2,2)使F'(β)<0,否则对

x∈(-2,2),F'(x)>0与F(-2)>F(2)矛盾.
因F'(α),F'(β)异号,
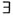
x
0∈(α,β)使得F'(x
0)=f'(x
0)(f"(x
0)+3f
2(x
0))=0,
即f"(x
0)+3f
2(x
0)=0.
[解析] 要证
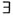
x
0∈(-2,2)使得f"(x
0)+3f
2(x
0)=0
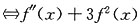
在(-2,2)内有零点
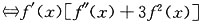
在(-2,2)内有零点x
0且f'(x
0)≠0
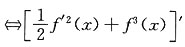
在(-2,2)内有零点x
0且f'(x
0)≠0.
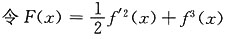
.要证F'(x)在(-2,2)内有零点,常用以下方法.
(1)证明
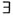
α,β∈(-2,2),α≠β,使得F(α)=F(β);
(2)证明
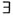
α,β∈(-2,2),α≠β,使得F'(α)F'(β)<0;
(3)证明
α,β∈(-2,2),F(x)在[α,β]的最大(小)值在(α,β)内取到.
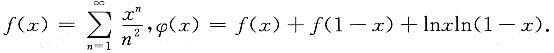 求:
求:7. φ(x)的定义域;
解:先求f(x)的定义域,即级数
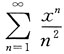
的收敛域,显然是[-1,1].
从而f(1-x)的定义域是-1≤1-x≤1,即0≤x≤2,lnxln(1-x)的定义域是{x>0}∩{x<1}={0<x<1}.
综上可知函数φ(x)的定义域是(0,1).
8. φ'(x).
解:
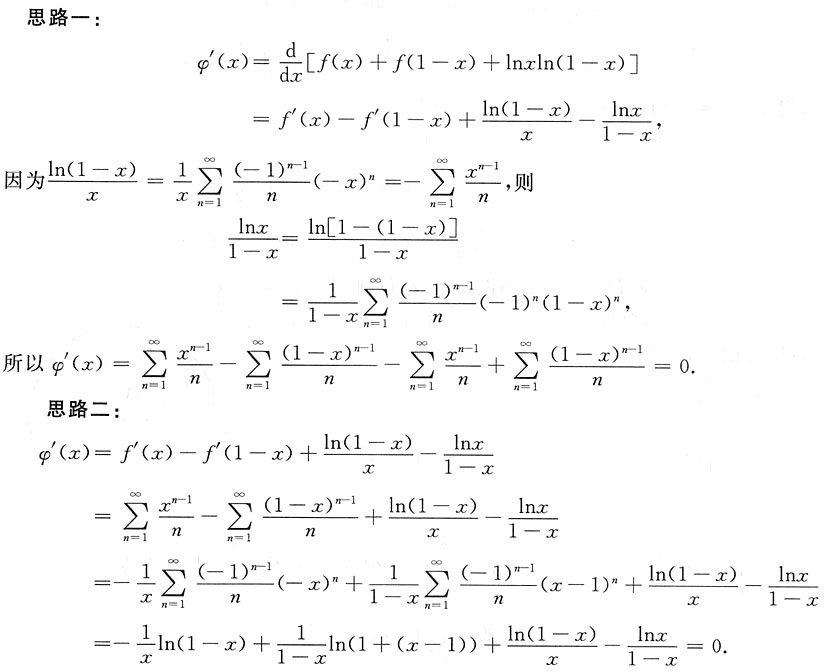
9. 设f(x,y)在点O(0,0)的某邻域U内连续,且
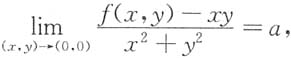
常数
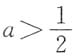
.试讨论f(0,0)是否为f(x,y)的极值?是极大值还是极小值?
解:由
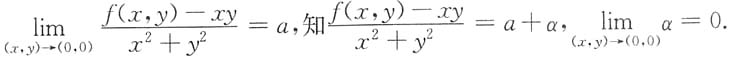
再令
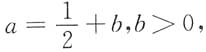
于是上式可改写为
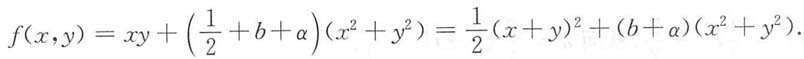
由f(x,y)的连续性,有
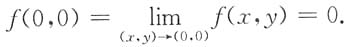
另一方面,由
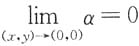
知,存在点(0,0)的去心邻域

当
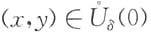
时,有
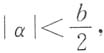
故在
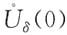
内,f(x,y)>0.所以f(0,0)是f(x,y)的极小值.
10. 设b>a>0,证明

证明:原不等式
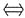
(a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).
令F(x)=(a+x)(lnx-lna)-2(x-a)>0,x>a,则F(x)在[a,+∞)上二阶可导,且
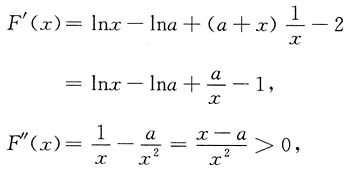
所以当x>a时,F'(x)单调增加,即
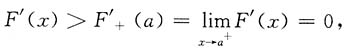
于是F(x)在[a,+∞)上单调增加,所以对b>a>0,有

即
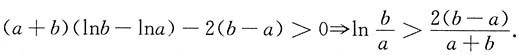
11. 已知f(x)是周期为5的连续函数,它在x=0的某邻域内满足关系式:f(1+sinx)-3f(1-sinx)=8x+a(x),其中α(x)是当x→0时比x高阶的无穷小,且f(x)在x=1处可导,求y=f(x)在点(6,f(6))处的切线方程.
解:求切线方程的关键是求斜率,因f(x)的周期为5,故在(6,f(6))处和点(1,f(1))处曲线有相同的斜率,根据已知条件求出f'(1).
由
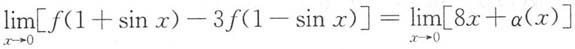
得f(1)-3f(1)=0,f(1)=0.又
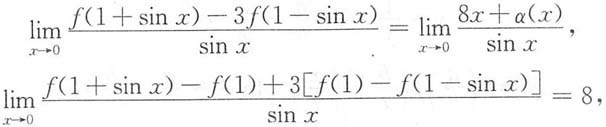
则4f'(1)=8,f'(1)=2,由f(6)=f(1)=0,f'(6)=f'(1)=2,故所求切线方程为y=2(x-6).
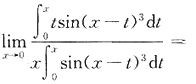
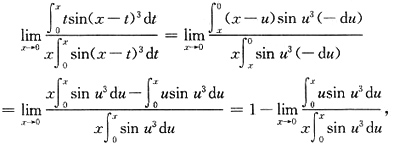
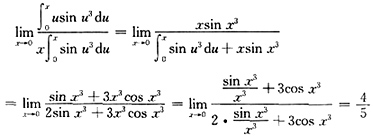
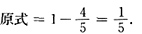
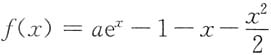 ,则f(x)在区间(-∞,+∞)内______
,则f(x)在区间(-∞,+∞)内______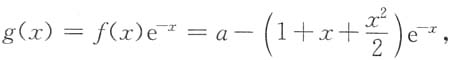 由于e-x>0,g(x)与f(x)的零点完全一样,又
由于e-x>0,g(x)与f(x)的零点完全一样,又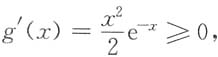 且仅在一点x=0等号成立,故g(x)严格单调增,所以g(x)至多有一个零点,从而f(x)至多有一个零点.
且仅在一点x=0等号成立,故g(x)严格单调增,所以g(x)至多有一个零点,从而f(x)至多有一个零点.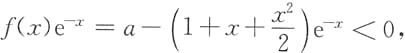 f(x)无零点.
f(x)无零点.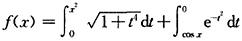 在区间(-∞,+∞)内零点个数为______
在区间(-∞,+∞)内零点个数为______ ,从而知在区间
,从而知在区间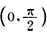 内f(x)至少有1个零点,又当x>0时,
内f(x)至少有1个零点,又当x>0时,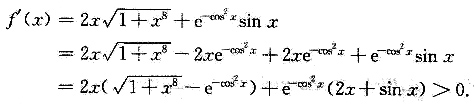
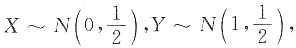 则与Z=Y-X同分布的随机变量是______.
则与Z=Y-X同分布的随机变量是______.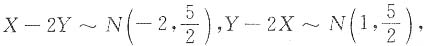 所以选B.
所以选B.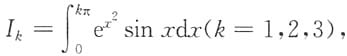 则有______
则有______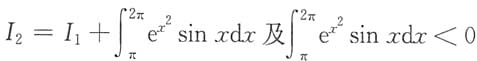 可得,I2<I1.
可得,I2<I1.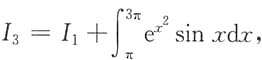 其中
其中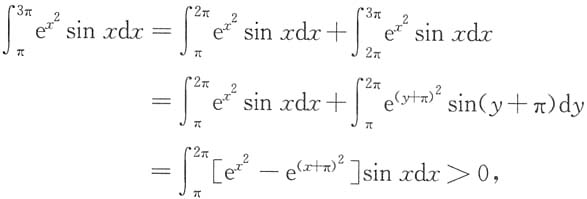
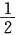
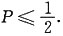
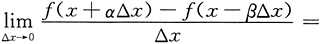 ______.
______.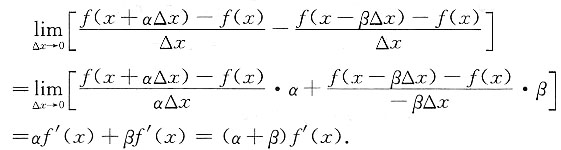
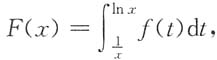 则F'(x)=______.
则F'(x)=______.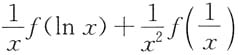
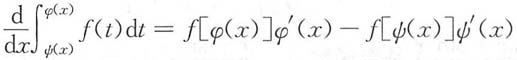 可知,
可知,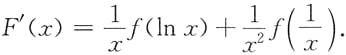
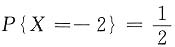 ,P{X=1}=a,P{X=3}=b,若E(X)=0,则D(X)=______.
,P{X=1}=a,P{X=3}=b,若E(X)=0,则D(X)=______.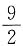 .
.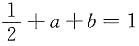 ,又EX=0,则
,又EX=0,则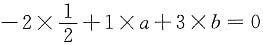 ,即a+3b=1.联立方程
,即a+3b=1.联立方程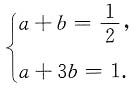
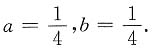

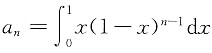 ,n=1,2,….则
,n=1,2,….则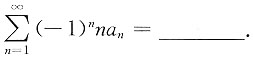
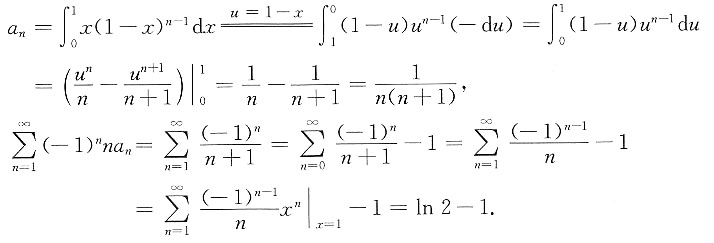
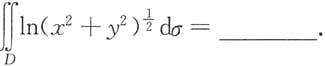
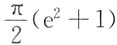
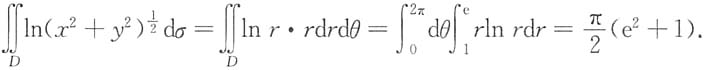
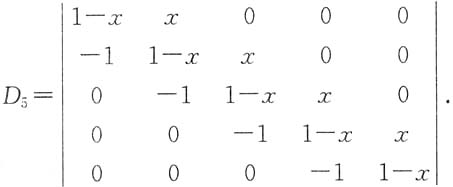
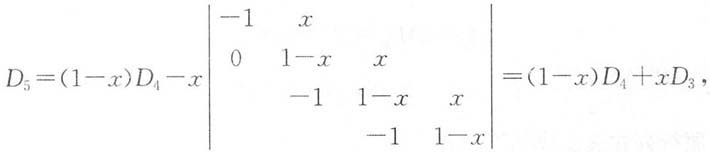
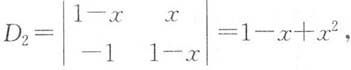 D1=1-x,于是得
D1=1-x,于是得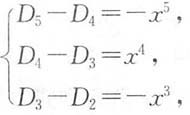
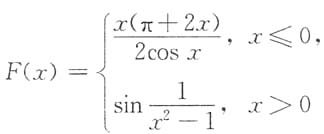 的间断点,并判断它们的类型.
的间断点,并判断它们的类型.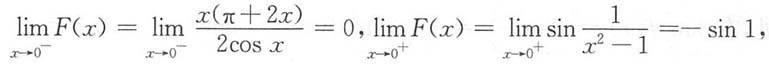 故x=0是函数F(x)的跳跃间断点.
故x=0是函数F(x)的跳跃间断点.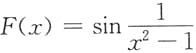 在x=1处没有定义,且极限
在x=1处没有定义,且极限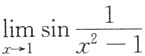 不存在.故x=1是函数F(x)的振荡间断点.
不存在.故x=1是函数F(x)的振荡间断点.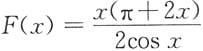 在点列
在点列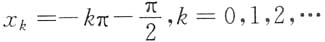 处没有定义,则这些点都是函数F(x)的间断点.特别对点
处没有定义,则这些点都是函数F(x)的间断点.特别对点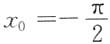 ,令
,令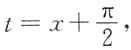 有
有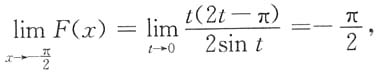
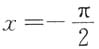 是函数F(x)的可去间断点;而点列
是函数F(x)的可去间断点;而点列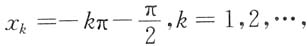 显然是函数F(x)的无穷间断点.
显然是函数F(x)的无穷间断点.
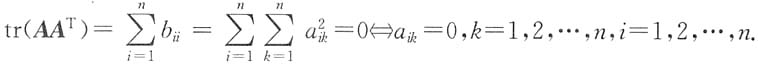
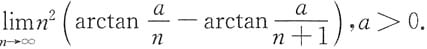
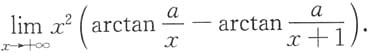 令f(t)=arctant,
令f(t)=arctant,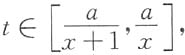 由拉格朗日中值定理可得
由拉格朗日中值定理可得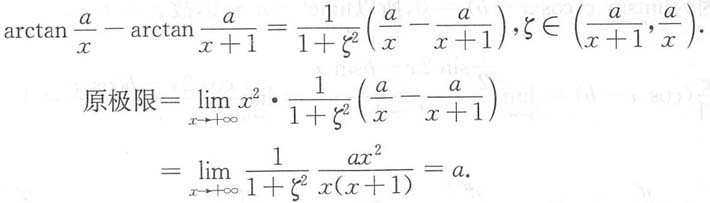

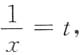 则
则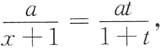 所以
所以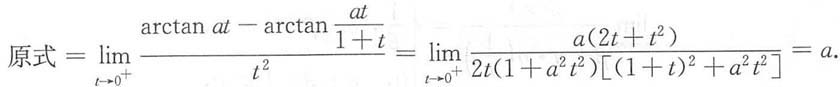
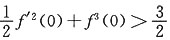 ,证明:
,证明: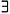 x0∈(-2,2),使得f"(x0)+3f2(x0)=0.
x0∈(-2,2),使得f"(x0)+3f2(x0)=0.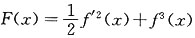 ,要证
,要证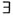 x0∈(-2,2),F'(x0)=0,f'(x0)≠0,我们用前面分析中指出的方法(3)来证明.
x0∈(-2,2),F'(x0)=0,f'(x0)≠0,我们用前面分析中指出的方法(3)来证明. α∈(-2,0),使得
α∈(-2,0),使得
 β∈[0,2]使得
β∈[0,2]使得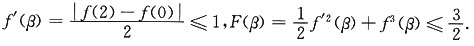
 在[α,β]上的最大值必在(α,β)中某点x0取到,于是F"(x0)=0,即f'(x0)(f"(x0)+3f2(x0))=0.
在[α,β]上的最大值必在(α,β)中某点x0取到,于是F"(x0)=0,即f'(x0)(f"(x0)+3f2(x0))=0.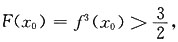 与|f(x)|≤1矛盾.
与|f(x)|≤1矛盾.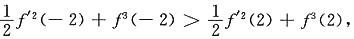
 a∈(-2,2)使得f"(a)≥0,证明:
a∈(-2,2)使得f"(a)≥0,证明: x0∈(-2,2)使得f"(x0)+3f2(x0)=0.
x0∈(-2,2)使得f"(x0)+3f2(x0)=0.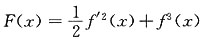 ,要证
,要证 x0∈(-2,2),使得F'(x0)=0.我们用分析中提到的方法(2)证明.
x0∈(-2,2),使得F'(x0)=0.我们用分析中提到的方法(2)证明. β∈(-2,2)使F'(β)<0,否则对
β∈(-2,2)使F'(β)<0,否则对 x∈(-2,2),F'(x)>0与F(-2)>F(2)矛盾.
x∈(-2,2),F'(x)>0与F(-2)>F(2)矛盾. x0∈(α,β)使得F'(x0)=f'(x0)(f"(x0)+3f2(x0))=0,
x0∈(α,β)使得F'(x0)=f'(x0)(f"(x0)+3f2(x0))=0,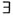 x0∈(-2,2)使得f"(x0)+3f2(x0)=0
x0∈(-2,2)使得f"(x0)+3f2(x0)=0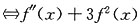 在(-2,2)内有零点
在(-2,2)内有零点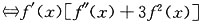 在(-2,2)内有零点x0且f'(x0)≠0
在(-2,2)内有零点x0且f'(x0)≠0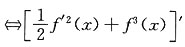 在(-2,2)内有零点x0且f'(x0)≠0.
在(-2,2)内有零点x0且f'(x0)≠0.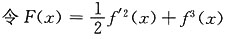 .要证F'(x)在(-2,2)内有零点,常用以下方法.
.要证F'(x)在(-2,2)内有零点,常用以下方法. α,β∈(-2,2),α≠β,使得F(α)=F(β);
α,β∈(-2,2),α≠β,使得F(α)=F(β); α,β∈(-2,2),α≠β,使得F'(α)F'(β)<0;
α,β∈(-2,2),α≠β,使得F'(α)F'(β)<0; α,β∈(-2,2),F(x)在[α,β]的最大(小)值在(α,β)内取到.
α,β∈(-2,2),F(x)在[α,β]的最大(小)值在(α,β)内取到.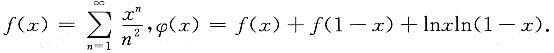 求:
求: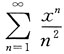 的收敛域,显然是[-1,1].
的收敛域,显然是[-1,1].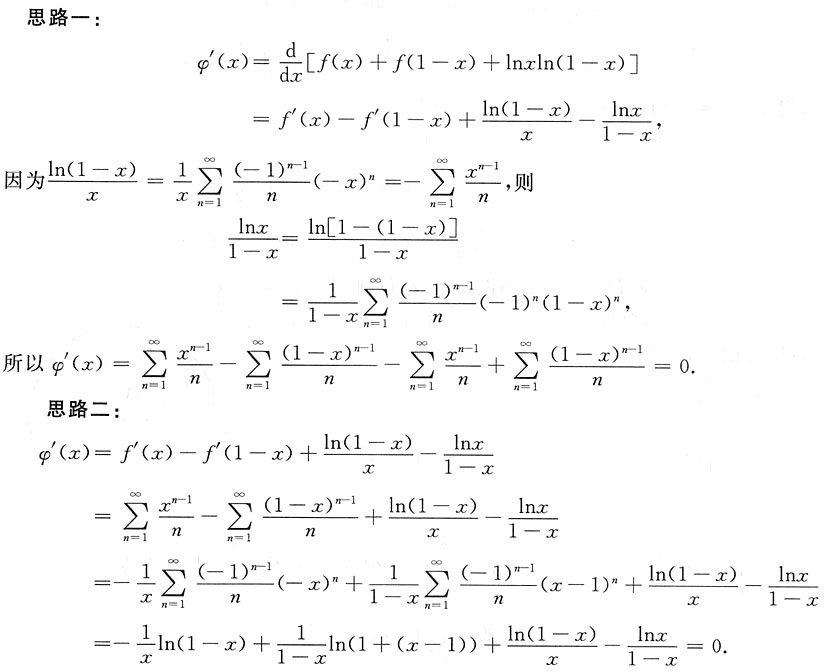
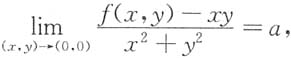 常数
常数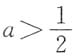 .试讨论f(0,0)是否为f(x,y)的极值?是极大值还是极小值?
.试讨论f(0,0)是否为f(x,y)的极值?是极大值还是极小值?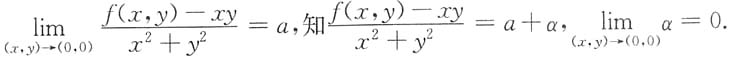
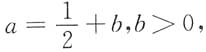 于是上式可改写为
于是上式可改写为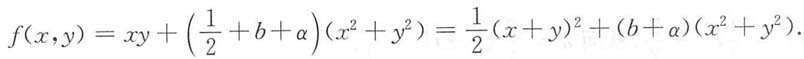
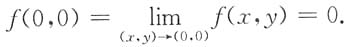
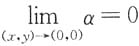 知,存在点(0,0)的去心邻域
知,存在点(0,0)的去心邻域 当
当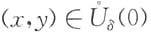 时,有
时,有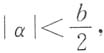 故在
故在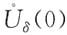 内,f(x,y)>0.所以f(0,0)是f(x,y)的极小值.
内,f(x,y)>0.所以f(0,0)是f(x,y)的极小值.
 (a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).
(a+b)(lnb-lna)-2(b-a)>0,将b改为x,则转化为函数不等式(a+x)(lnx-lna)-2(x-a)>0(x>a).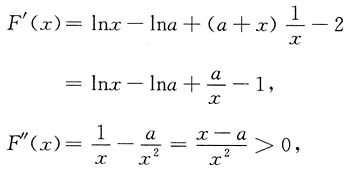
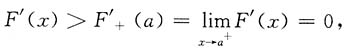

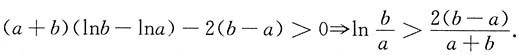
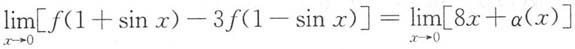 得f(1)-3f(1)=0,f(1)=0.又
得f(1)-3f(1)=0,f(1)=0.又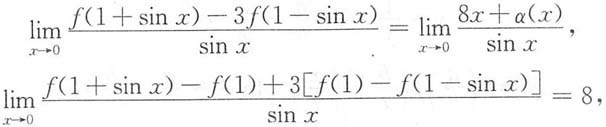 则4f'(1)=8,f'(1)=2,由f(6)=f(1)=0,f'(6)=f'(1)=2,故所求切线方程为y=2(x-6).
则4f'(1)=8,f'(1)=2,由f(6)=f(1)=0,f'(6)=f'(1)=2,故所求切线方程为y=2(x-6).