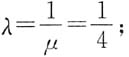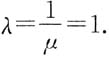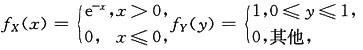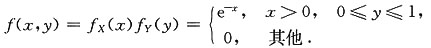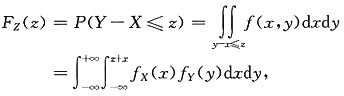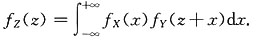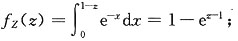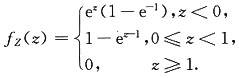一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.2. 已知α
1=[-1,1,a,4]
T,α
2=[-2,1,5,a]
T,α
3=[a,2,10,1]
T是4阶方阵A的3个不同特征值对应的特征向量,则a的取值为______
- A.a≠5
- B.a≠-4
- C.a≠3
- D.a≠-3且a≠-4
A B C D
A
[解析] α
1,α
2,α
3是三个不同特征值的特征向量,必线性无关,由

知a≠5.故应选(A).
3. 已知y
1=xe
x+e
2x,y
2=xe
x+e
-x是二阶非齐次线性微分方程的解,则此方程为______
- A.y"-y'-2y=ex-2xex.
- B.y"+y'+2y=ex-2xex.
- C.y"-y'-2y=-ex+2xex.
- D.y"+y'+2y=-ex+2xex.
A B C D
A
[解析] y
1-y
2=e
2x-e
-x为对应齐次方程的解.
特征方程为(λ-2)(λ+1)=0,即λ
2-λ-2=0,故对应的齐次方程为y"-y'-2y=0.
代入y
1,有
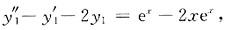
故非齐次方程为y"-y'-2y=e
x-2xe
x,选A.
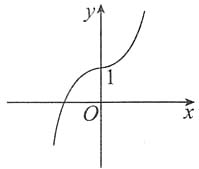
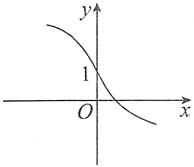
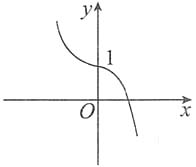
4. 函数y=f(x)满足条件f(0)=1,f'(0)=0,当x≠0时,f'(x)>0,
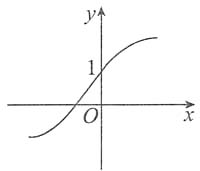
则它的图形是______
A.
B.
C.
D.
A B C D
B
[解析] 因函数单调增加,且在x=0处有水平切线,选(B).
5. 差分方程y
t-2y
t-1=b(b为常数)的通解是______.
- A.yt=A2t+b
- B.yt=2t-b
- C.yt=A(-2)t+b
- D.yt=A2t-b
A B C D
D
[解析] 所给差分方程视为y
t-2y
t-1=b·1
t.因2≠1(特征根不等于底数),故其特解形式为
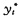
=C(C为待定常数),代入差分方程即得C=2C=b,C=-b,故
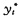
=-b.
易知其齐次方程的通解为
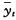
=A·2
t.
又

=-b,故其通解为
y
t=
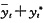
=A·2
t-b,其中A为任意常数.仅D入选.
6. 已知函数
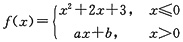
在(-∞,+∞)内连续可导,则______.
- A.a=2,b=3
- B.a=-2,b=3
- C.a=3,b=2
- D.a=-3,b=-2
A B C D
A
[解析] 下面介绍一个简化左、右导数计算的方法:
(1)设f(x)在[x
0,x
0+δ](δ>0)上连续,在(x
0,x
0+δ)内可导,且
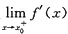
存在,则
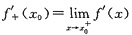
;
(2)设f(x)在[x
0-δ,x
0](δ>0)上连续,在(x
0-δ,x
0)内可导,且
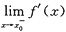
存在,则
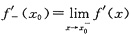
.
可用上法求之,也可用左、右导数定义求出a、b.
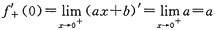
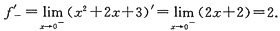
因f(x)在x=0处可导,故f'
-(0)=f'
+(0),即a=2.
又因f(x)在x=0处连续,故f(0+0)=f(0-0),即
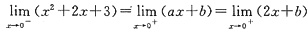
故3=b.仅A入选.
8. A是m×n矩阵,线性方程组AX=b有唯一解的充分必要条件是______.
- A.m=n且|A|≠0
- B.导出组AX=0有且仅有零解
- C.A的列向量组α1,α2,…,αn与α1,α2,…,αn,b等价
- D.r(A)=n,且b可由A的列向量组线性表出
A B C D
D
[解析] 利用AX=b有唯一解的充分必要条件是
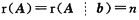
去判别.
当m=n时,必有
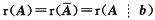
,
因而必有解。又|A|≠0,即m=n=r(A),则AX=b必有唯一解.这也可由克拉默法则得知,但并不必要,当m≠n时,方程组也可能有唯一解.例如
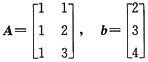
,AX=b有唯一解.
C是AX-b有唯一解的必要条件,并非充分条件,即两个向量组α
1,α
2,…,α
n与α
1,α
2,…,α
n,b等价是方程组AX=b有解的充要条件,是有唯一解的必要条件.例如
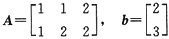
AX=b有解,但解不唯一.
B是AX-b有唯一解的必要条件,并非充分条件.因这时不能保证r(A)=r(A
b).如AX=0有非零解,则AX=b必没有唯一解,它可能有无穷多解,亦可能无解,当AX=0只有零解时,AX=b可能有唯一解,也可能无解,并不能保证必有唯一解.例如
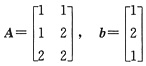
AX=0仅有零解,而AX=b并无解.
D秩r(A)=n表明A的列向量组线性无关,因而如AX=b有解,则解必唯一.仅r(A)=n还不能保证r(A)=
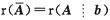
,因而不能保证AX=b有解(参见B中反例),b可由A的列向量组线性表出是AX=b有解的充要条件,这两个条件结合才能保证
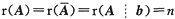
.因而它们才是AX=b有唯一解的充要条件,仅D入选.
[注意] B、C均是必要条件,前者不能保证r(A)=
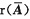
,因而不能保证AX=b必有解,后者不能保证AX=b的解唯一.A的列向量线性相关,AX=b绝对没有唯一解,列向量组线性无关最多有唯一解.
二、填空题1. f(t)为连续函数,D是由y=x
3,y=1,x=-1围成的区域,则
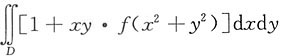
=______.
2
[解析] 如下图,由区域的对称性可得
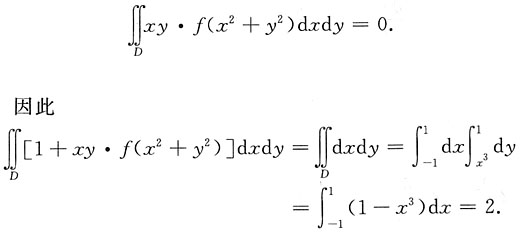
2. 设A,B是两个随机事件,且P(A)+P(B)=0.8,P(A+B)=0.6,则
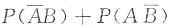
=______.
0.4
[解析] 因为P(A+B)=P(A)+P(B)-P(AB),且P(A)+P(B)=0.8,P(A+B)=0.6,所以P(AB)=0.2.又因为
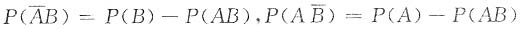
,所以
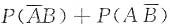
=P(A)+P(B)-2P(AB)=0.8-0.4=0.4.
3. 设
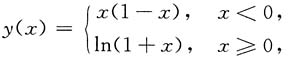
则与直线2x+y=1垂直的曲线y(x)的切线方程为______.
[解析] 由已知得
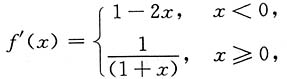
由于曲线y(x)切线的斜率应为
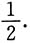
当x<0时,
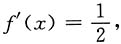
无解.
当x≥0时,
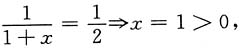
由此得切点为P(1,ln2).
所求切线方程为
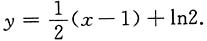
4. 设

B=(E+A)
-1(E-A),则(E+B)
-1=______.
[解析] E+B=E+(E+A)
-1(E-A)=(E+A)
-1(E+A+E-A)=(E+A)
-12E,
故
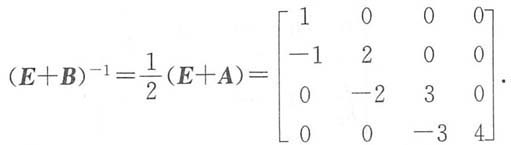
5. 函数
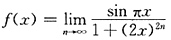
的间断点的个数为______.
2
[解析] 应先写出f(x)的表达式:
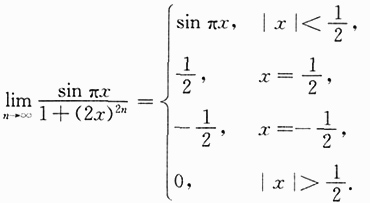
故知正好有两个间断点
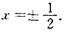
6. 设A是3阶矩阵,其特征值是1,2,-1,那么(A+2E)
2的特征值是______.
9,16,1
[解析] 设矩阵A属于特征值λi的特征向量是αi,那么
(A+2E)αi=Aαi+2αi=(λi+2)αi,
(A+2E)2αi=(A+2E)(λi+2)αi=(λi+2)(A+2E)αi=(λi+2)2αi.
由于αi≠0,故αi是矩阵(A+2E)2属于特征值(λi+2)2的特征向量,即矩阵(A+2E)2的特征值是9,16,1.
 ______
______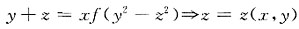 .
.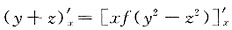 ,得
,得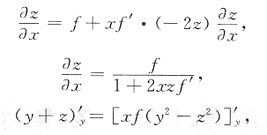


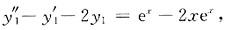 故非齐次方程为y"-y'-2y=ex-2xex,选A.
故非齐次方程为y"-y'-2y=ex-2xex,选A. 则它的图形是______
则它的图形是______



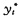 =C(C为待定常数),代入差分方程即得C=2C=b,C=-b,故
=C(C为待定常数),代入差分方程即得C=2C=b,C=-b,故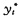 =-b.
=-b.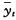 =A·2t.
=A·2t. =-b,故其通解为
=-b,故其通解为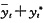 =A·2t-b,其中A为任意常数.仅D入选.
=A·2t-b,其中A为任意常数.仅D入选.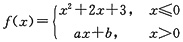
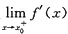 存在,则
存在,则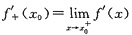 ;
;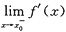 存在,则
存在,则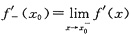 .
.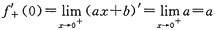
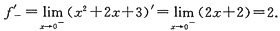
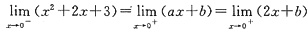
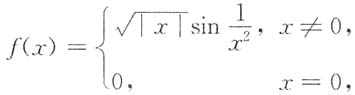 则f(x)在点x=0处______
则f(x)在点x=0处______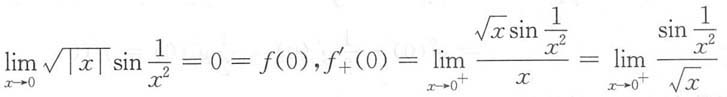 不存在,故f'(0)不存在.
不存在,故f'(0)不存在.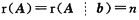 去判别.
去判别.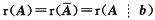 ,
,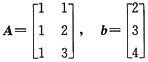 ,AX=b有唯一解.
,AX=b有唯一解.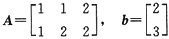 AX=b有解,但解不唯一.
AX=b有解,但解不唯一. b).如AX=0有非零解,则AX=b必没有唯一解,它可能有无穷多解,亦可能无解,当AX=0只有零解时,AX=b可能有唯一解,也可能无解,并不能保证必有唯一解.例如
b).如AX=0有非零解,则AX=b必没有唯一解,它可能有无穷多解,亦可能无解,当AX=0只有零解时,AX=b可能有唯一解,也可能无解,并不能保证必有唯一解.例如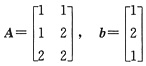
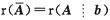 ,因而不能保证AX=b有解(参见B中反例),b可由A的列向量组线性表出是AX=b有解的充要条件,这两个条件结合才能保证
,因而不能保证AX=b有解(参见B中反例),b可由A的列向量组线性表出是AX=b有解的充要条件,这两个条件结合才能保证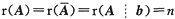 .因而它们才是AX=b有唯一解的充要条件,仅D入选.
.因而它们才是AX=b有唯一解的充要条件,仅D入选.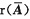 ,因而不能保证AX=b必有解,后者不能保证AX=b的解唯一.A的列向量线性相关,AX=b绝对没有唯一解,列向量组线性无关最多有唯一解.
,因而不能保证AX=b必有解,后者不能保证AX=b的解唯一.A的列向量线性相关,AX=b绝对没有唯一解,列向量组线性无关最多有唯一解.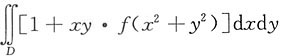 =______.
=______.
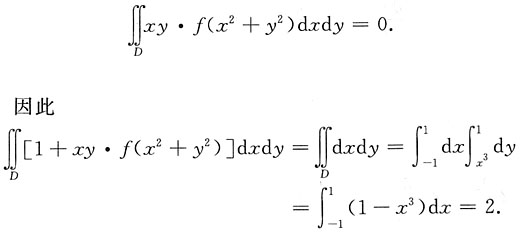
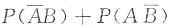 =______.
=______.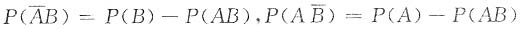 ,所以
,所以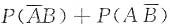 =P(A)+P(B)-2P(AB)=0.8-0.4=0.4.
=P(A)+P(B)-2P(AB)=0.8-0.4=0.4.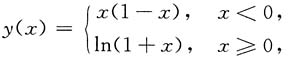 则与直线2x+y=1垂直的曲线y(x)的切线方程为______.
则与直线2x+y=1垂直的曲线y(x)的切线方程为______.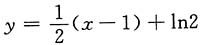
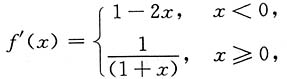 由于曲线y(x)切线的斜率应为
由于曲线y(x)切线的斜率应为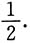
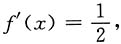 无解.
无解.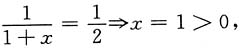 由此得切点为P(1,ln2).
由此得切点为P(1,ln2).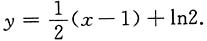
 B=(E+A)-1(E-A),则(E+B)-1=______.
B=(E+A)-1(E-A),则(E+B)-1=______.
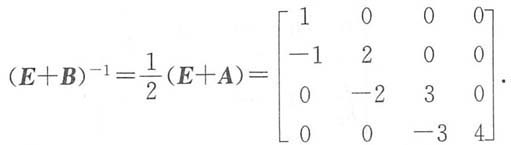
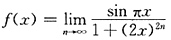 的间断点的个数为______.
的间断点的个数为______.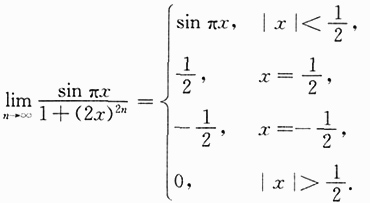
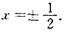
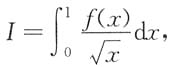 其中
其中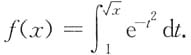
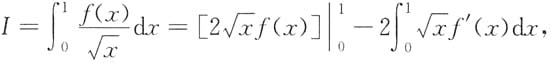
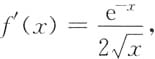 故
故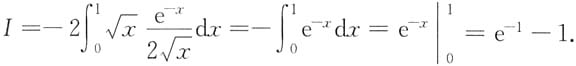
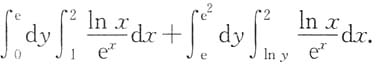
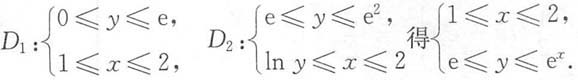 则D=D1+D2:
则D=D1+D2: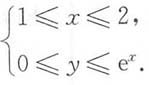 所以
所以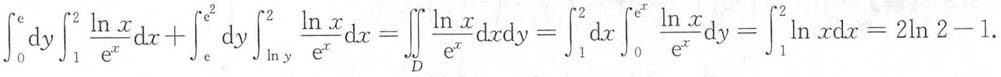
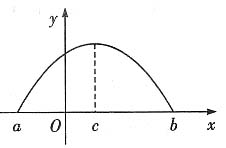
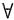 子区间上Φ"(x)
子区间上Φ"(x)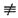 0,又Φ(a)=Φ(b)=0,求证Φ(x)>0(x∈(a,b)).
0,又Φ(a)=Φ(b)=0,求证Φ(x)>0(x∈(a,b)).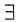 c∈(a,b),Φ'(c)=0.由Φ'(x)在[a,b]↘,
c∈(a,b),Φ'(c)=0.由Φ'(x)在[a,b]↘,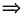
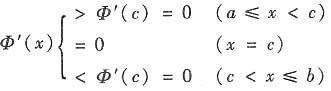
 Φ(x)在[a,c]↗,在[c,b]↘,
Φ(x)在[a,c]↗,在[c,b]↘,
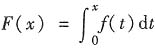 满足
满足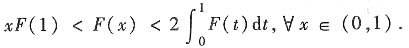
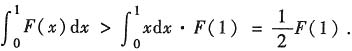
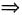
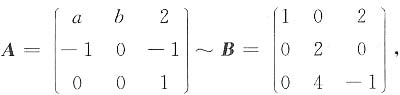 求a,b及可逆矩阵P,使得P-1AP=B.
求a,b及可逆矩阵P,使得P-1AP=B.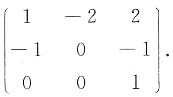
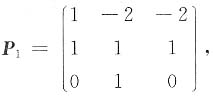 则
则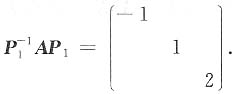
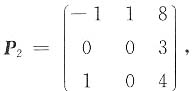 则
则
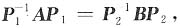 得
得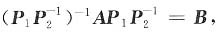
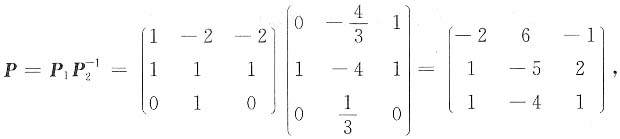 则P-1AP=B.
则P-1AP=B.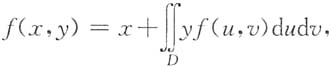 其中D由
其中D由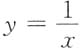 ,x=1.y=2围成,求f(x,y).
,x=1.y=2围成,求f(x,y).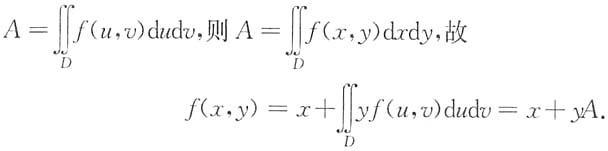
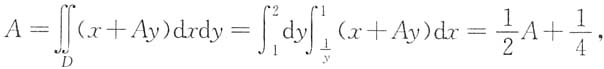 从而
从而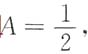 故
故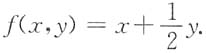
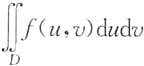 是一个常数,因此
是一个常数,因此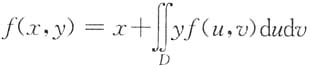 变为
变为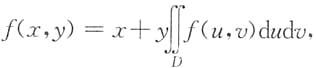 两边再求二重积分就可以解决了.
两边再求二重积分就可以解决了.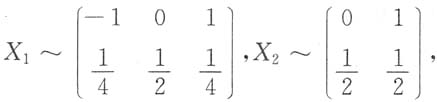 而且P{X1X2=0}=1.
而且P{X1X2=0}=1.
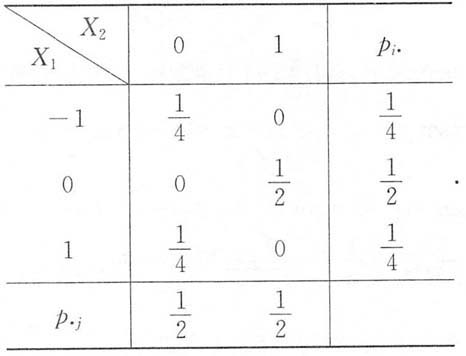
 而
而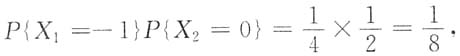
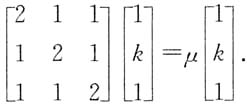
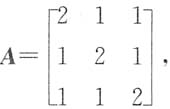 求k及α所对应的特征值.
求k及α所对应的特征值.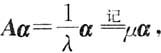 即
即