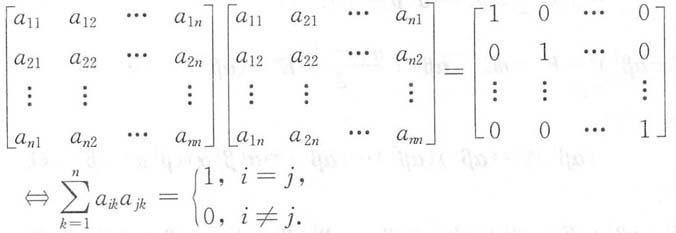一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 设f(x)是偶函数,
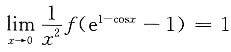
,则f(x)在x=0处______
- A.可导.
- B.连续,左、右两侧导数都存在,但不相等.
- C.连续,左、右两侧导数都不存在.
- D.不连续.
A B C D
B
[解析] 令t=e
1-cosx-1,x→0
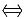
t→0
+,f(0)=0.
因为
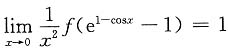
,所以

由于
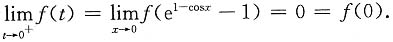
所以f(x)在x=0处右连续.
由于f(x)是偶函数,
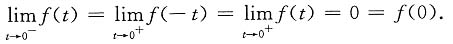
因此f(x)在x=0处连续.
又
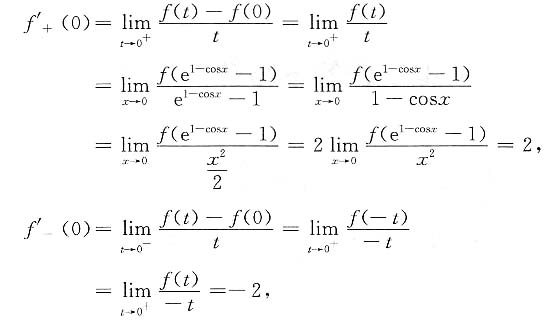
所以f'
-(0)≠f'
+(0).
综上,知f(x)在x=0处连续,左右导数存在但不相等.
2. 设y(x)是微分方程y"+(x-1)y'+x
2y=e
x满足初始条件y(0)=0,y'(0)=1的解,则
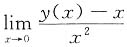
______.
A B C D
A
[解析] 微分方程y"+(x-1)y'+x
2y=e
x中,令x=0,则y"(0)=2,于是
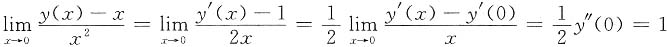
,选A.
4. 设F(x)可导,则下述命题不正确的是______
- A.若F(x)为奇函数,则F'(x)必为偶函数.
- B.若F'(x)为偶函数,则F(x)必为奇函数.
- C.若F(x)为偶函数,则F'(x)必为奇函数.
- D.若F'(x)为奇函数,则F(x)必为偶函数.
A B C D
B
[解析] A,C,D都是正确的,证明如下:
A是正确的.设F(x)为奇函数:F(-x)=-F(x),
两边对x求导,得-F'(-x)=-F'(x),即F'(-x)=F'(x).
故知F'(x)是偶函数.
C是正确的,设F(x)为偶函数:F(-x)=F(x),
两边对x求导,得-F'(-x)=F'(x),
所以F'(x)是奇函数.
D是正确的.设F'(x)为奇函数,令f(x)=F'(x),即设f(x)为奇函数:
f(-x)=-f(x),
两边对t从0到x积分,得
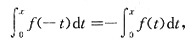
左边作积分变量变换,令-t=u,得
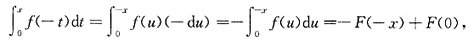
右边
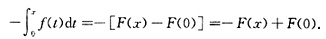
所以得到F(-x)=F(x),
即F(x)为偶函数.
B是不正确的,反例:设F'(x)=x
2为偶函数,
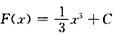
未必是奇函数.
5. 设随机变量X,Y相互独立,且X~N(0,1),Y~N(1,1),则______.
A.P(X+Y≤0)=
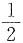
B.P(X+Y≤1)=
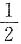
C.P(X-Y≤0)=
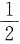
D.P(X-Y≤1)=
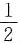
A B C D
B
[解析] X,Y独立,X~N(0,1),Y~N(1,1),X+Y~N(1,2)
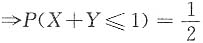
,所以选B.
6. 设三阶矩阵A的特征值为-1,1,2,其对应的特征向量为α
1,α
2,α
3,令P=(3α
2,-α
3,2α
1),则P
-1AP等于______.
A.

B.

C.

D.
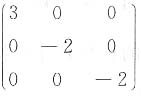
A B C D
C
[解析] 显然3α
2,-α
3,2α
1也是特征值1,2,-1的特征向量,所以
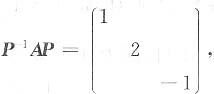
选C.
二、填空题1. 微分方程
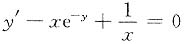
的通解为______.
[解析] 由
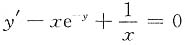
,得
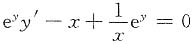
,即
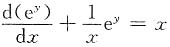
,
令z=e
y,则
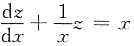
,解得
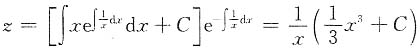
,
所以原方程的通解为
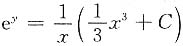
.
2. 已知离散型随机变量X的可能取值为-1,0,1,且EX=0.1,DX=0.89,则D(X
2)=______.
0.09
[解析] 设对应于-1,0,1的概率分别为p
1,p
2,p
3,则p
1+p
2+p
3=1.
由于EX=-p
1+p
3=0.1.又因为
E(X
2)=(EX)
2+DX=0.1
2+0.89=0.9,
故p
1+p
3=0.9,所以得
p
1=0.4,p
2=0.1,p
3=0.5.
因此可以得到X的分布列为
进而得到X
2的分布列为
所以D(X
2)=0.09.
3. 设z=x(x,y)由方程
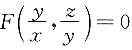
确定,并设F(u,v)对u,v具有连续的一阶偏导数,且在运算的过程中出现的分母均不为零,则
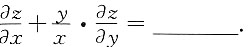
[解析] 方程
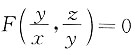
两边分别对x,y求一阶偏导数.z=z(x,y)看成由此式确定的隐函数,有
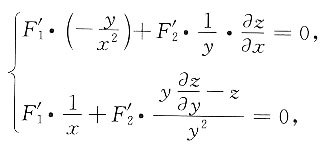
解得
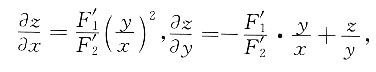
则
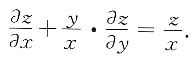
4.
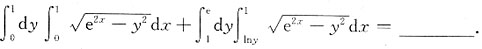
[解析] D
1={(x,y)|0≤x≤1,0≤y≤1},
D
2={(x,y)lny≤x≤1,1≤y≤e},
D=D
1∪D
2 ={(x,y)|0≤y≤e
x,0≤x≤1}(如下图).
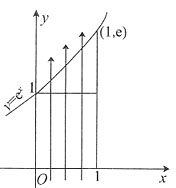
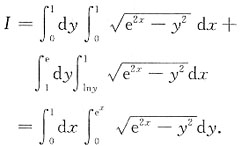
而
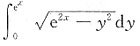
可看作半径为e
x的圆的面积的
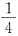
,即为
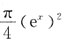
.
因而
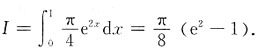
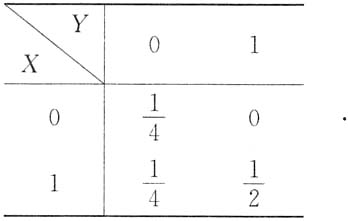
5. 设随机变量X与Y的分布律为
且相关系数
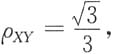
则(X,Y)的分布律为______.
[解析] 设(X,Y)的分布律为
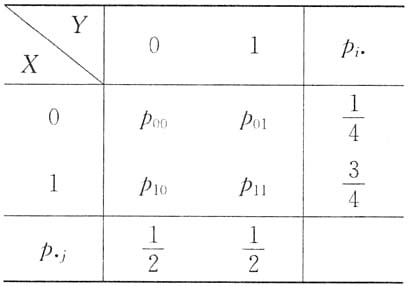
((X,Y)的边缘分布律也表示于表中),
则E(XY)=p
11,从而有
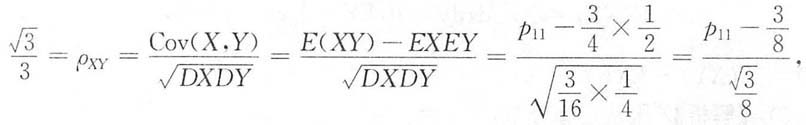
由此得
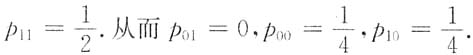
所以(X,Y)的分布律为
三、解答题共94分,解答应写出文字说明、证明过程或验算步骤.1. 设A是s×n矩阵,B是A的前m行构成的m×n矩阵,已知A的行向量组的秩为r.证明:r(B)≥r+m-s。
证明:因(A的行向量的个数s)-(A的线性无关行向量的个数r(A))≥(B的行向量个数m)-(B的线性无关的行向量的个数r(B)),
即 s-r(A)≥m-r(B),
得 r(B)≥r(A)+m-s=r+m-s.
2. 计算
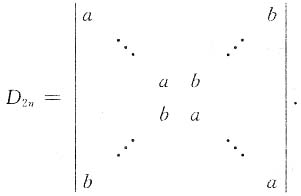
解:方法一

方法二 D
2n=a
2D
2n-2-b
2D
2n-2=(a
2-b
2)D
2n-2=…=(a
2-b
2)
n
3. 若x>-1.证明:
当0<α<1时,有(1+x)
α<1+αx;当α<0或α>1时,有(1+x)
α>1+αx.
证明:令f(x)=(1+x)
α,则有f'(x)=α(1+x)
α-1,f"(x)=α(α-1)(1+x)
α-2.
由f(x)的泰勒展开式
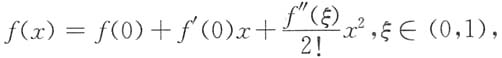
可知当x>-1,0<α<1时,α(α-1)<0,1+ξ>0,故

所以f(x)<f(0)+f'(0)x,即
(1+x)
α<1+αx.
同理可证当x>-1,α<0或α>1时,有(1+x)
α>1+αx.
4. 用变量代换x=lnt将方程
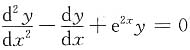
化为y关于t的方程,并求原方程的通解.
解:
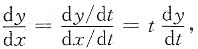
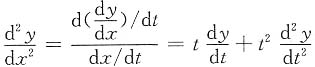
,代入原方程得
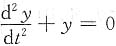
.
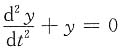
的通解为y=C
1cost+C
2sint,
故原方程的通解为y=C
1cose
x+C
2sine
x.
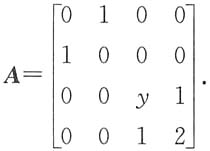
5. 已知A的一个特征值为3,试求y;
解:
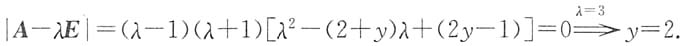
6. 求矩阵P,使(AP)
T(AP)为对角矩阵.
解:A为对称矩阵,要使(AP)
T(AP)=P
TA
2P为对角矩阵,即将实对称矩阵A
2对角化.
由上小题得A的特征值λ
1=-1,λ
2,3=1,λ
4=3,故A
2的特征值λ
1,2,3=1,λ
4=9.且
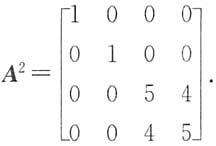
A
2的属于特征值λ
1,2,3=1的正交单位化的特征向量为
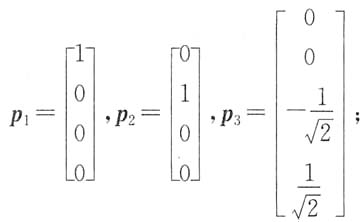
A
2的属于特征值λ
4=9的正交单位化的特征向量为
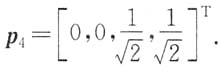

8. 若f(x)在(-∞,+∞)上连续,且
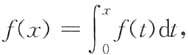
试证:
f(x)≡0(-∞<x<+∞).
证明:由
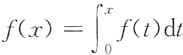
可知f'(x)=f(x),其通解为f(x)=ce
x,又f(0)=0,故f(x)≡0.
9. 设A是n阶矩阵,r(A)=n-r.又Ax=b有α
1,α
2,…,α
r,α
r+1共r+1个线性无关解.
证明Ax=b的任一解均可由α
1,α
2,…,α
r,α
r+1线性表出.
证明:由解的性质知,αr+1-α1,αr+1-α2,…,αr+1-αr是对应齐次方程Ax=0的r个解.
令k1(αr+1-α1)+k2(αr+1-α2)+…+kr(αr+1-αr)=0,即
(k1+k2+…+kr)αr+1-(k1α1+k2α2+…+krαr)=0
因α1,α2,…,αr,αr+1线性无关,得k1=k2=…=kr=0,故知αr+1-α1,αr+1-α2,…,αr+1-αr,是Ax=0的r个线性无关解,又因r(A)=n-r,故知是Ax=0的基础解系,从而Ax=b的通解是
l1(αr+1-α1)+l2(αr+1-α2)+…+lr(αr+1-αr)+αr+1=-l1α1-l2α2-…-lrαr+(l1+l2+…+lr)αr+1.
即Ax=b的任一解均可由α1,α2,…,αr,αr+1线性表出.
10. 证明:方阵A是正交矩阵,即AA
T=E的充分必要条件是:(1)A的列向量组组成标准正交向量组,即
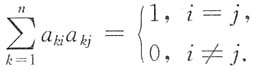
或(2)A的行向量组组成标准正交向量组,即
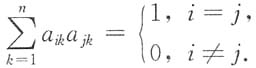
证明:设
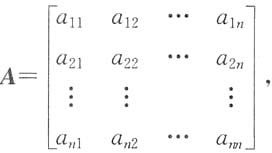
且A是正交矩阵.
(1)AA
T=E,A,A
T互为逆矩阵,有A
TA=E,故

(2)AA
T=E,即
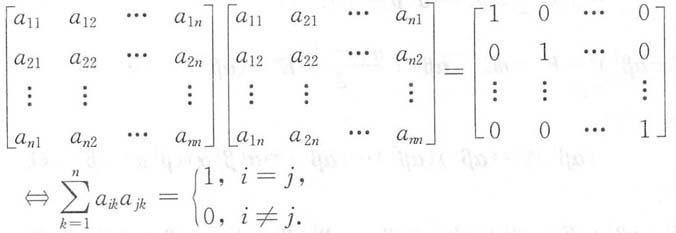
11. 设A是n(n≥3)阶矩阵.证明:(A
*)
*=|A|
n-2A.
证明:(A*)*A*=|A*|E=|A|n-1E,当r(A)=n时,r(A*)=n,A*=|A|A-1,则(A*)*A*=(A*)*|A|A-1=|A|n-1E,故(A*)*=|A|n-2A.当r(A)=n-1时,|A|=0,r(A*)=1,r[(A*)*]=0,即(A*)*=0,原式显然成立.当r(A)<n-1时,|A|=0,r(A*)=0,(A*)*=O,原式也成立.
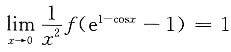 ,则f(x)在x=0处______
,则f(x)在x=0处______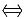 t→0+,f(0)=0.
t→0+,f(0)=0.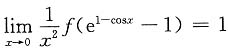 ,所以
,所以
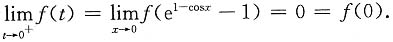 所以f(x)在x=0处右连续.
所以f(x)在x=0处右连续.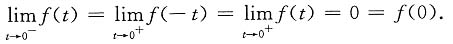
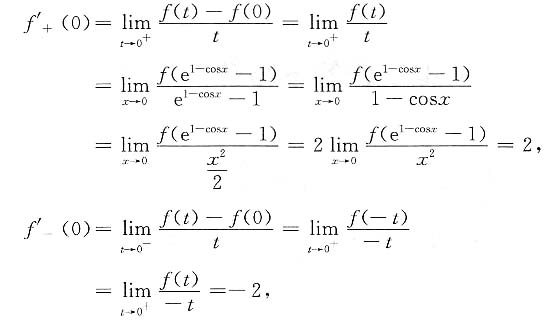
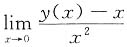 ______.
______.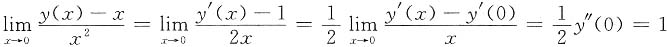 ,选A.
,选A.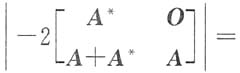 ______
______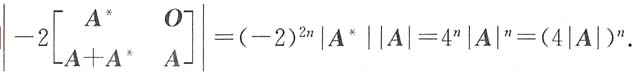
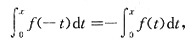
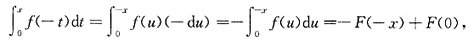
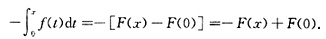
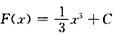 未必是奇函数.
未必是奇函数.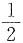
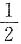
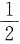
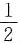
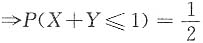 ,所以选B.
,所以选B.


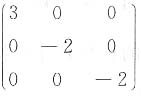
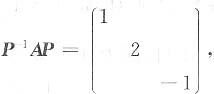 选C.
选C.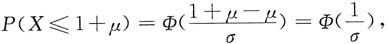 而标准正态分布函数是严格的增函数.
而标准正态分布函数是严格的增函数.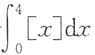 的值为______
的值为______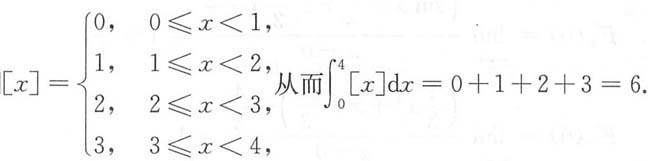
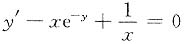 的通解为______.
的通解为______.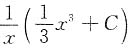
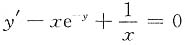 ,得
,得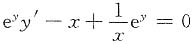 ,即
,即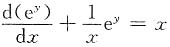 ,
,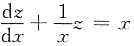 ,解得
,解得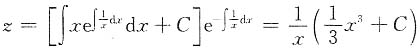 ,
,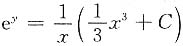 .
.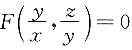 确定,并设F(u,v)对u,v具有连续的一阶偏导数,且在运算的过程中出现的分母均不为零,则
确定,并设F(u,v)对u,v具有连续的一阶偏导数,且在运算的过程中出现的分母均不为零,则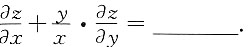
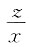
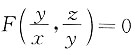 两边分别对x,y求一阶偏导数.z=z(x,y)看成由此式确定的隐函数,有
两边分别对x,y求一阶偏导数.z=z(x,y)看成由此式确定的隐函数,有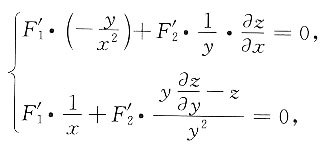
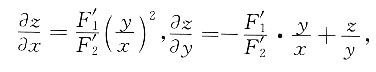
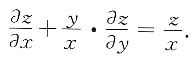
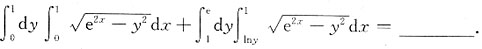
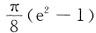

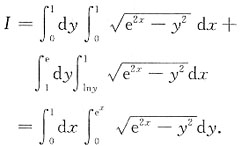
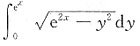 可看作半径为ex的圆的面积的
可看作半径为ex的圆的面积的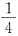 ,即为
,即为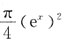 .
.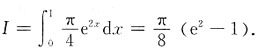
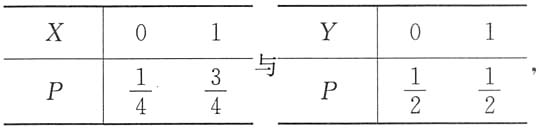
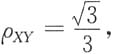 则(X,Y)的分布律为______.
则(X,Y)的分布律为______.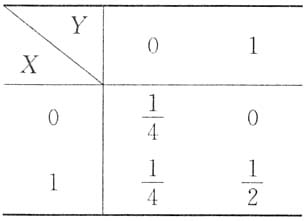

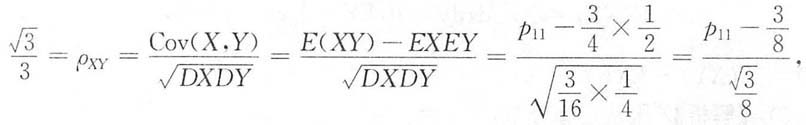
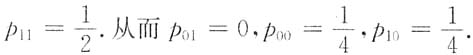 所以(X,Y)的分布律为
所以(X,Y)的分布律为
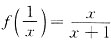 ,则
,则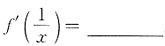 .
.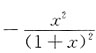
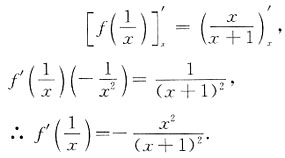


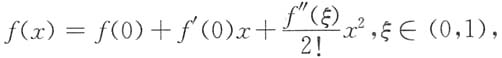
 所以f(x)<f(0)+f'(0)x,即
所以f(x)<f(0)+f'(0)x,即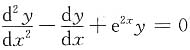 化为y关于t的方程,并求原方程的通解.
化为y关于t的方程,并求原方程的通解.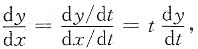
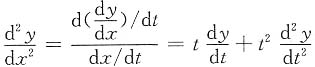 ,代入原方程得
,代入原方程得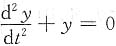 .
.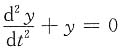 的通解为y=C1cost+C2sint,
的通解为y=C1cost+C2sint,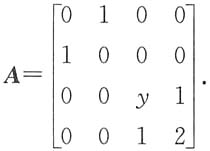
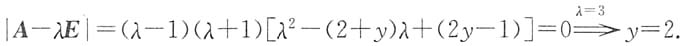
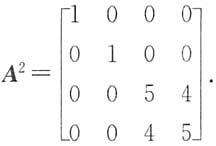

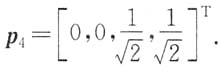

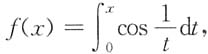 试证:f'(0)=0.
试证:f'(0)=0.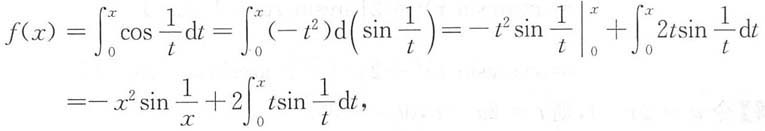
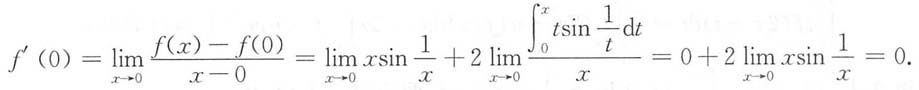
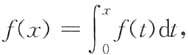 试证:
试证: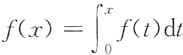 可知f'(x)=f(x),其通解为f(x)=cex,又f(0)=0,故f(x)≡0.
可知f'(x)=f(x),其通解为f(x)=cex,又f(0)=0,故f(x)≡0.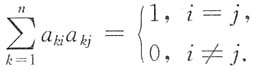 或(2)A的行向量组组成标准正交向量组,即
或(2)A的行向量组组成标准正交向量组,即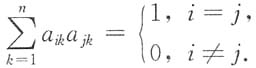
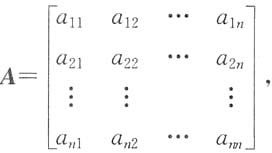 且A是正交矩阵.
且A是正交矩阵.