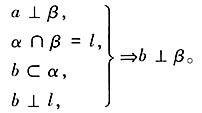银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
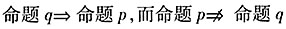 ,即p是q的必要不充分条件。
,即p是q的必要不充分条件。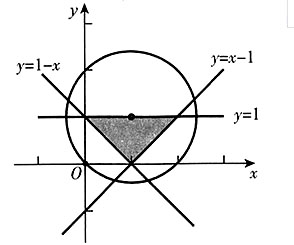
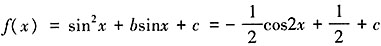 ,此时f(x)的最小正周期
,此时f(x)的最小正周期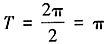 ;当b≠0时,
;当b≠0时,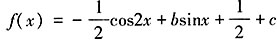 ,此时cos2x的最小正周期为π,bsinx的最小正周期为2π,所以f(x)的最小正周期为2π。故f(x)的最小正周期与b有关,但与c无关。故本题选B。
,此时cos2x的最小正周期为π,bsinx的最小正周期为2π,所以f(x)的最小正周期为2π。故f(x)的最小正周期与b有关,但与c无关。故本题选B。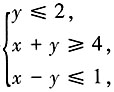 则z=3x+y的最大值为______。
则z=3x+y的最大值为______。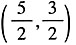 。z为直线y=-3x+z在y轴的截距。从图中可以看出,当直线y=-3x+z经过点(3,2)时,其在y轴的截距最大,所以zmax=(3x+y)|(3,2)=3×3+2=11。故本题选B。
。z为直线y=-3x+z在y轴的截距。从图中可以看出,当直线y=-3x+z经过点(3,2)时,其在y轴的截距最大,所以zmax=(3x+y)|(3,2)=3×3+2=11。故本题选B。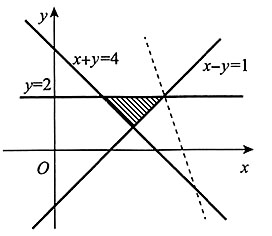
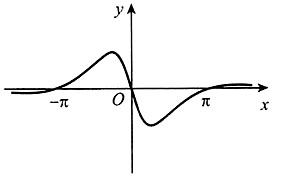
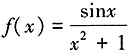 的图像大致为______。
的图像大致为______。
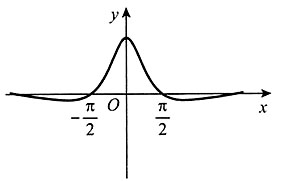
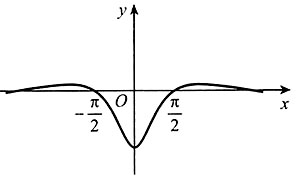
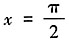 时,
时,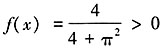 ,所以排除B项。故本题选A。
,所以排除B项。故本题选A。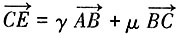 ,则γ+μ的值为______。
,则γ+μ的值为______。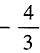
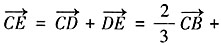
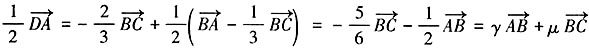 ,即
,即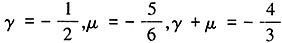 。
。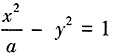 的左顶点为A。若双曲线的一条渐近线与直线AM平行,则实数a=______。
的左顶点为A。若双曲线的一条渐近线与直线AM平行,则实数a=______。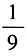
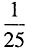
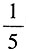
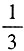
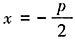 。由抛物线的定义可得
。由抛物线的定义可得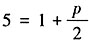 ,故p=8,所以抛物线的方程为y2=16x,进而可求得M(1,4)。双曲线
,故p=8,所以抛物线的方程为y2=16x,进而可求得M(1,4)。双曲线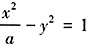 的左顶点为
的左顶点为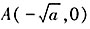 ,渐近线方程为
,渐近线方程为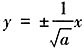 ,直线AM的斜率为
,直线AM的斜率为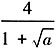 。由双曲线的一条渐近线与直线AM平行,可得
。由双曲线的一条渐近线与直线AM平行,可得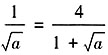 ,解得
,解得 。故本题选A。
。故本题选A。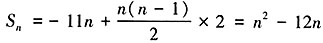 。由此可知,当
。由此可知,当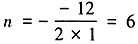 时,Sn取得最小值。故本题选A。
时,Sn取得最小值。故本题选A。 ,则|z|=______。
,则|z|=______。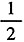
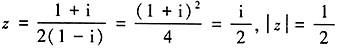 。
。 ,
,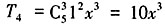 ,则(1-2x)(1+x)5的展开式中,x3项的系数为10+(-2)×10=-10。
,则(1-2x)(1+x)5的展开式中,x3项的系数为10+(-2)×10=-10。 。如图,现在等边△ABC内射入一个点,则该点落在△ABC内切圆中的概率是______。
。如图,现在等边△ABC内射入一个点,则该点落在△ABC内切圆中的概率是______。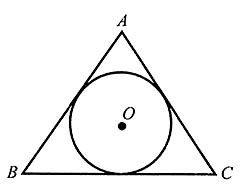
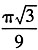
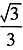 ,所以所求概率
,所以所求概率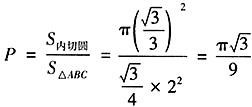 。
。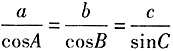 ,△ABC为______三角形。
,△ABC为______三角形。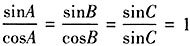 ,进而有tanA=tanB=1,则
,进而有tanA=tanB=1,则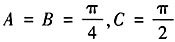 ,故△ABC为等腰直角三角形。
,故△ABC为等腰直角三角形。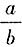 的值;
的值;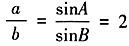 。
。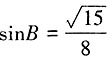 ,求c。
,求c。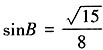 ,则
,则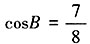 。由余弦定理可知,
。由余弦定理可知,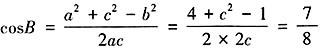 ,解得c=2或
,解得c=2或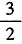 。
。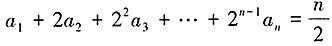 ,n∈N*。
,n∈N*。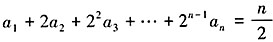 ①,又n≥2,
①,又n≥2,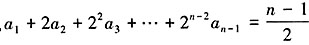 ②,由①-②得,
②,由①-②得,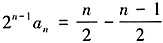 ,整理得
,整理得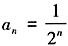 ,验证n=1时,
,验证n=1时, 满足
满足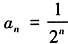 。故数列{an}的通项公式为
。故数列{an}的通项公式为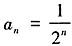 。
。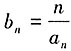 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。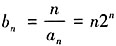 ,Sn=1×21+2×22+3×23+…+n2n③,2Sn=1×22+2×23+3×24+…+n2n+1④,由③-④得,-Sn=1×2+22+23+…+2n-n2n+1=-2+(1-n)2n+1,Sn=(n-1)2n+1+2。
,Sn=1×21+2×22+3×23+…+n2n③,2Sn=1×22+2×23+3×24+…+n2n+1④,由③-④得,-Sn=1×2+22+23+…+2n-n2n+1=-2+(1-n)2n+1,Sn=(n-1)2n+1+2。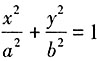 (a>b>0)的离心率
(a>b>0)的离心率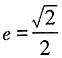 ,左、右焦点分别为F1,F2,点
,左、右焦点分别为F1,F2,点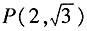 ,F2在线段PF1的中垂线上。
,F2在线段PF1的中垂线上。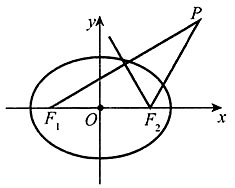
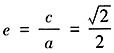 ,椭圆的焦点F1(-c,0),F2(c,0)。因为F2在线段PF1的中垂线上,所以F1F1=PF2,即有
,椭圆的焦点F1(-c,0),F2(c,0)。因为F2在线段PF1的中垂线上,所以F1F1=PF2,即有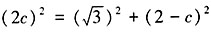 ,解得c=1或
,解得c=1或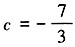 (舍去)。所以
(舍去)。所以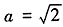 ,b2=a2-c2=2-1=1。椭圆的方程为
,b2=a2-c2=2-1=1。椭圆的方程为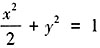 。
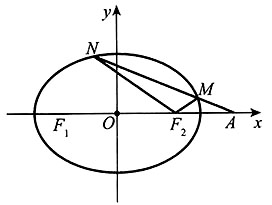
。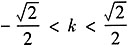 。又由已知,得k≠0。
。又由已知,得k≠0。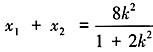 ①,
①,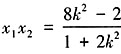 ②。注意到∠NF2A≠90°,则直线NF2和直线MF2的斜率都存在,记为kNF2,kMF2。所以要证∠NF2F1=∠MF2A,只要证kNF2=-kMF2,即
②。注意到∠NF2A≠90°,则直线NF2和直线MF2的斜率都存在,记为kNF2,kMF2。所以要证∠NF2F1=∠MF2A,只要证kNF2=-kMF2,即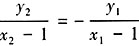 ③。整理③式得2x1x2-3(x1+x2)+4=0④,将①②代入④可得
③。整理③式得2x1x2-3(x1+x2)+4=0④,将①②代入④可得 ,即证得等式③恒成立,也即kNF2=-kMF2。所以满足题意k的取值范围为
,即证得等式③恒成立,也即kNF2=-kMF2。所以满足题意k的取值范围为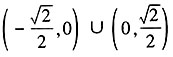 。
。
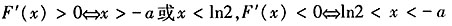 ,所以函数F(x)在(-∞,ln2)和(-a,+∞)上单调递增,在(ln2,-a)上单调递减;③当-a<ln2时,有
,所以函数F(x)在(-∞,ln2)和(-a,+∞)上单调递增,在(ln2,-a)上单调递减;③当-a<ln2时,有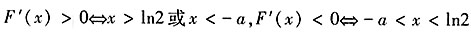 ,所以函数F(x)在(-∞,-a)和(ln2,+∞)上单调递增,在(-a,ln2)上单调递减。
,所以函数F(x)在(-∞,-a)和(ln2,+∞)上单调递增,在(-a,ln2)上单调递减。
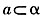 。
。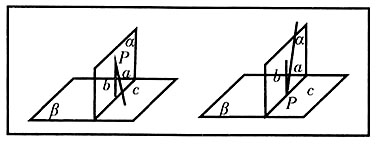
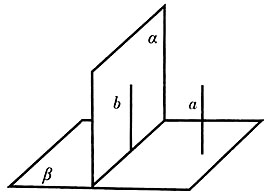
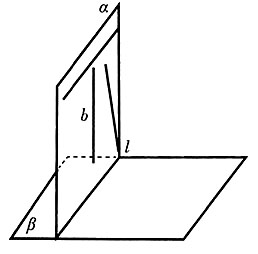
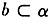 ,α⊥β,是否可以得到b⊥β?
,α⊥β,是否可以得到b⊥β?