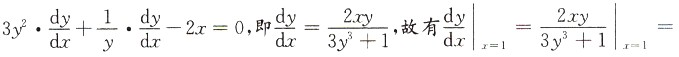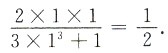第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)1.
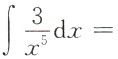
______
A.
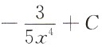
B.
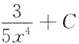
C.
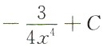
D.
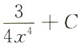
A B C D
C
[考点] 本题考查了不定积分的知识点.
[解析]
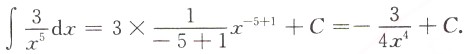
2. 设函数f(x)=2lnx,则f"(x)=______
A.
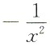
B.
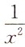
C.
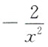
D.
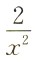
A B C D
C
[考点] 本题考查了二阶导函数的知识点.
[解析]
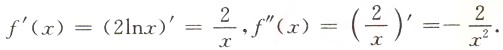
4. 设函数f(x)=3+x
5,则f'(x)=______
A.5x
4 B.
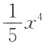
C.1+x
4 D.x
4 A B C D
A
[考点] 本题考查了一阶导数的知识点.
[解析] f'(x)=(3+x5)'=5x4.
9.

______
A.2
B.1
C.
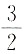
D.
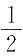
A B C D
C
[考点] 本题考查了分式函数的极限的知识点.
[解析]
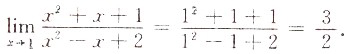
10. 微分方程y'+y=0的通解为y=______
A B C D
D
[考点] 本题考查了微分方程的通解的知识点.
[解析] 原微分方程分离变量得

两边积分
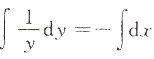
解得ln|y|=-x+lnC
1,即|y|=C
1e
-x,令C=±C
1,则有y=Ce
-x.
第Ⅱ卷(非选择题)
二、填空题1.
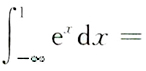
______.
e
[考点] 本题考查了反常积分的知识点.
[解析]
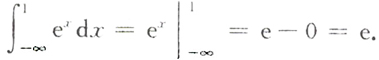
2. 设函数y=e
2x,则dy=______.
2e2xdx
[考点] 本题考查了函数微分的知识点.
[解析] y'=(e2x)'=2e2x,故dy=y'dx=2e2xdx.
3.
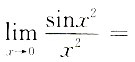
______.
1
[考点] 本题考查了函数极限的知识点.
[解析] x→0时,x
2→0,故有
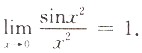
4. ∫(3x+2sinx)dx=______.
[考点] 本题考查了不定积分的知识点.
[解析]
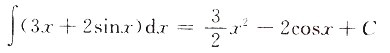
5. 曲线y=arctan(3x+1)在点
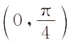
处切线的斜率为______.
[考点] 本题考查了曲线的切线的知识点.
[解析] y'=[arctan(3x+1)]'=

,故曲线在点
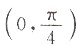
处的切线斜率为y'|
x=0=
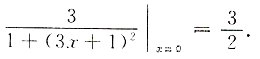
6. 若函数
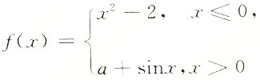
在x=0处连续,则a=______.
-2
[考点] 本题考查了分段函数连续性的知识点.
[解析] 由于f(x)在x=0处连续.故有

,而f(0)=-2.
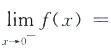

,因此a=-2.
7. 过点(-1,2,3)且与直线
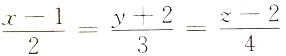
垂直的平面方程为______.
2x+3y+4z=16
[考点] 本题考查了平面方程的知识点.
[解析] 已知直线与所求平面垂直,故所求平面的法向量为n=(2,3,4),因此所求平面的方程为2(x+1)+3(y-2)+4(z-3)=0,即2x+3y+4z=16.
8. 函数f(x)=x
3-6x的单调递减区间为______.
[考点] 本题考查了函数的单调性的知识点.
[解析] 易知f'(x)=3x
2-6,令f'(x)<0,则有
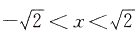
,故f(x)的单调递减区间为
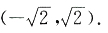
9. 区域D={(x,y)|1≤x≤2,1≤y≤x
2的面积为______.
[考点] 本题考查了定积分的应用的知识点.
[解析] 区域D的面积为
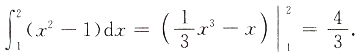
10. 方程y
3+lny-x
2=0在点(1,1)的某邻域确定隐函数y=y(x),则
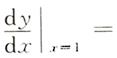
______.
[考点] 本题考查了隐函数求导的知识点.
[解析] 方程两边对x求导,得