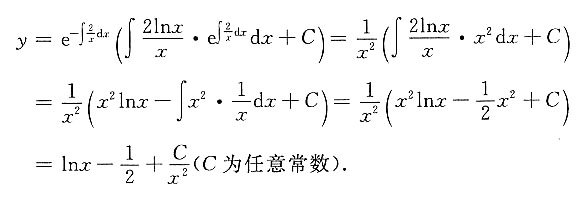一、单项选择题3. 设z=x
2ln(x
2+y
2)，则
=______
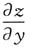
A．
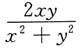
B．
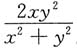
C．
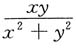
D．
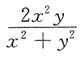
A B C D
D
[解析]
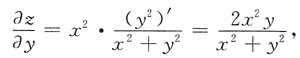
故应选D．
6. 设函数f(xy,x-y)=x
2+y
2，则
=______
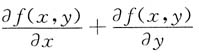
- A.2x+2y
- B.2+2y
- C.2x-2y
- D.2-2y
A B C D
B
[解析] 因为f(xy，x-y)=x
2+y
2=(x-y)
2+2xy，所以f(x，y)=y
2+2x，
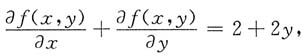
故应选B．
7. 函数z=f(x，y)在点P
0(x
0，y
0)处的两个偏导数
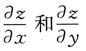
存在是它在P
0处可微的______
A B C D
B
[解析]
故应选B．
8. 设y=x
3+3
x+log
3x+3，则dy=______
A．
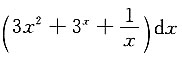
B．
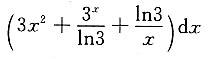
C．
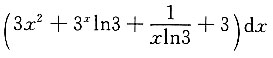
D．
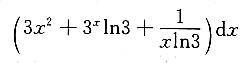
A B C D
D
[解析]
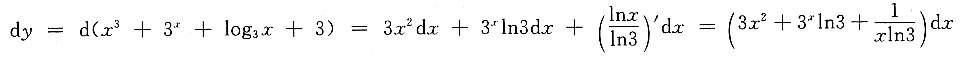
．故应选D．
9. 掷两枚均匀的硬币，出现“一正一反”的概率是______
A．
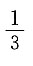
B．
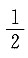
C．
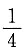
D．
A B C D
B
[解析]
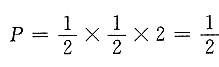
，故选B．
10. 二元函数
在点(0，0)处______
- A.连续，偏导数存在
- B.连续，偏导数不存在
- C.不连续，偏导数存在
- D.不连续，偏导数不存在
A B C D
C
[解析] 因为
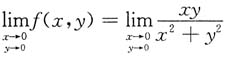
不存在(若沿x轴→(0，0)时，极限为0，若沿直线y=x→(0，0)时，极限为
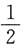
，所以在(0，0)点函数无极限)．所以函数在(0，0)点处不连续．
而
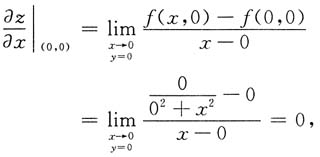
同理
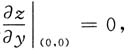
偏导数在(0，0)点处存在．
二、填空题1. 设某商品的需求函数为Q=100-2P，则当价格P=25时，其边际收入为______．
0
[解析] 总收益TR=PQ=100P-2P2，则边际收益MR=(TR)'=100-4P，当P=25时，边际收入为0．
2. 极限
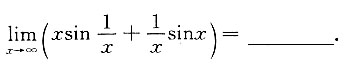
1
[解析]
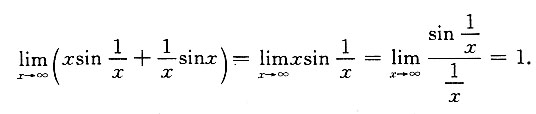
3. 已知当x→0时，f(x)与1-cosx为等价无穷小，则
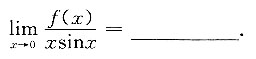
[解析] 当x→0时
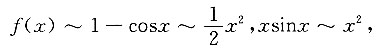
所以
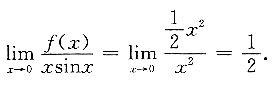
4.
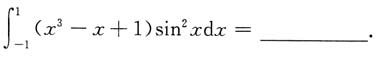
[解析]
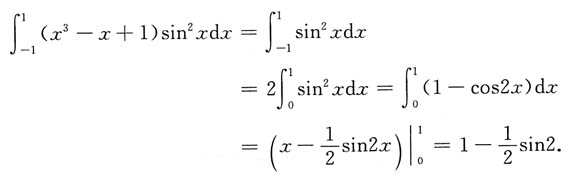
5.
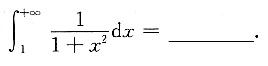
[解析]
6. 设区域D为x
2+y
2≤1，则
=______．
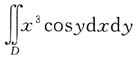
0
[解析] 因为区域D是关于y轴对称的，而被积函数满足f(-x，y)=-f(x，y)．
根据二重积分的对称性可知
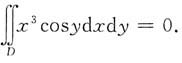
7. 设z=e
-x-(x-2y)tan(xy)，则
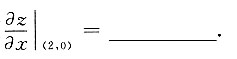
-e-2
[解析] z(x，0)=e
-x，所以
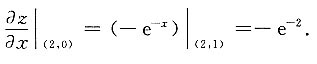
8. 设
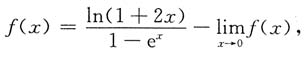
则f(x)=______．
9. 设向量b和a={1，-2，3}共线，且a·b=56，则b=______．
4a
[解析] 因为b与a共线，所以b=λa={λ，-2λ，3λ}，由a·b=1×λ+(-2)×(-2λ)+3×3λ=56，得λ=4，所以b={4，-8，12}或者b=4a．
10. 已知
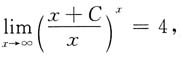
则C=______．
2ln2
[解析]
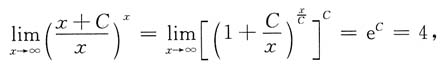
所以C=2ln2．
三、解答题3. 将
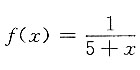
展开成关于x的幂级数，并指出收敛区间．
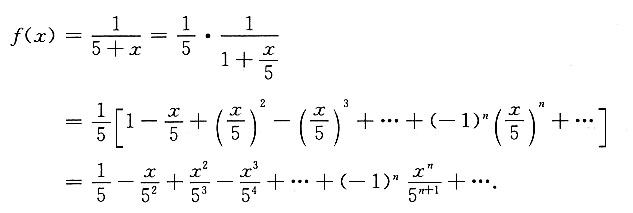
收敛区间为x∈(-5，5)．
4. 求微分方程xdy+2(y-lnx)dx=0的通解．
方程可化为
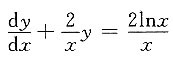
，所求通解为
则一定成立的是______
知当x→2时，
即在x=2的某去心邻域内有f"(x)＜0，故应选D．
深色：已答题 浅色：未答题