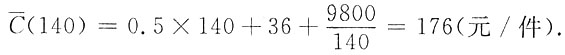银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
河北省专升本高等数学(二)模拟22
一、单项选择题
(在每小题给出的四个备选项中，选出一个正确的答案)
1. 设f(x)在[a，b]上连续，在(a，b)内可导，且f(a)=f(b)，则曲线y=f(x)在(a，b)内平行于x轴的切线______
A.仅有一条
B.至少一条
C.有两条
D.不存在
A
B
C
D
B
[解析] 由题设知，f(x)在[a，b]上满足罗尔定理的条件，由定理的几何意义知，平行于x轴的切线至少有一条．故选B．
2. 若f(x)在点x=a的邻域内有定义，且
，则以下结论正确的是______
A.f(x)在点a的邻域内单调增加
B.f(x)在点a的邻域内单调减少
C.f(a)为函数f(x)的极大值
D.f(a)为函数f(x)的极小值
A
B
C
D
D
[解析] 因为
，根据保号性可知在点x=a的去心邻域内有f(x)-f(a)＞0，即f(x)＞f(a)，所以f(a)为函数的极小值，故选D．
3. 若行列式
，则x=______
A.-3
B.-2
C.2
D.3
A
B
C
D
D
[解析]
所以x=3．
4. 设A，B，C，I为同阶方阵，I为单位矩阵，若ABC=I，则下列各式中总成立的是______
A.ACB=I
B.BAC=I
C.BCA=I
D.CBA=I
A
B
C
D
C
[解析] 由ABC=A(BC)=I，可知A可逆，且A
-1
=BC，则(BC)A=I，故选C．
5. 已知f'(0)=a，g'(0)=b，且f(0)=g(0)，则
=______
A.a-b
B.2a+b
C.a+b
D.b-a
A
B
C
D
C
[解析]
故选C．
6. 设函数
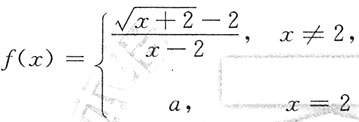
在x=2处连续，则a=______
A．4
B．
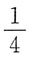
C．2
D．
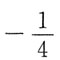
A
B
C
D
B
[解析]
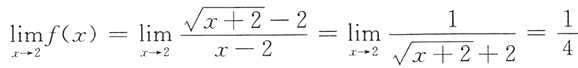
，又f(2)=a，根据连续的定义得
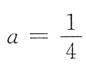
，故选B．
7. 设
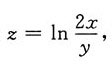
则dz|
(1，2)
=______
A．
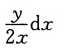
B．
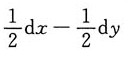
C．
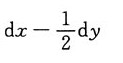
D．
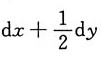
A
B
C
D
C
[解析] 因f(x，2)=lnx，所以
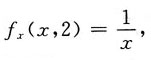
故f
x
(1，2)=1；
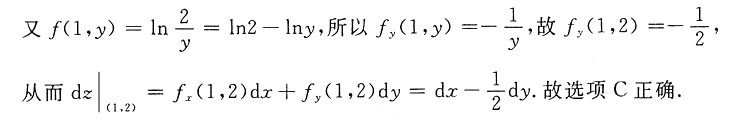
8. 若级数
收敛，则下列级数中收敛的是______
A．
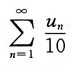
B．
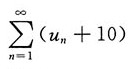
C．
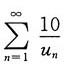
D．
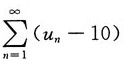
A
B
C
D
A
[解析] 根据无穷级数的运算性质可以判定
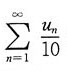
收敛，而其他选项均发散．故选A．
9. 若当x→0时，kx+2x
2
+3x
3
与x是等价无穷小，则常数k=______
A.0
B.1
C.2
D.3
A
B
C
D
B
[解析]
故选B．
10. 设A为三阶矩阵，|A|=2，其伴随矩阵为A*，则(A*)*=______
A.2A
B.4A
C.8A
D.16A
A
B
C
D
A
[解析] A*=|A|A
-1
=2A
-1
，
二、填空题
1. 已知
则p=______.
[解析]
2. 幂级数
的收敛域为______．
[解析] 因为
所以收敛半径
收敛区间为
当
时，该级数为交错级数
收敛；
当
时，该级数为调和级数
发散．
故该幂级数的收敛域是
3. 矩阵
的秩为______．
2
[解析]
，故r(A)≠3．
，故A有二阶行列式不为零的子阵，所以r(A)=2．
4.
的值等于______．
e
ab
[解析]
5. 函数y=x
2
在[1，3]上的平均值为______．
[解析] y=x
2
在[1，3]上的平均值为
三、计算题
(每小题10分，共40分．将解答的主要过程、步骤和答案填写在相应位置上)
1. 求微分方程xy'+y=4x
3
+3x
2
+2x+1的通解．
解：将原方程改写成
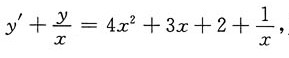
则
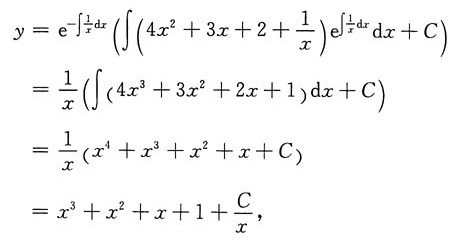
其中C为任意常数．
已知线性方程组
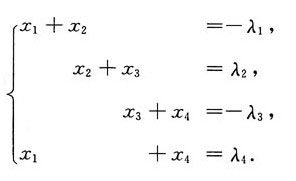
2. 当λ
1
，λ
2
，λ
3
，λ
4
满足什么条件时，该线性方程组有解?
解：对线性方程组所对应的增广矩阵B进行初等行变换
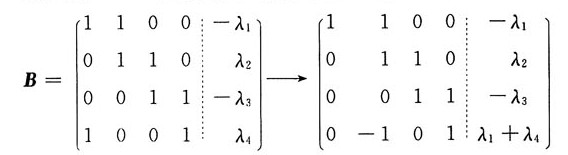
由于方程组有解，故必有λ
1
+λ
2
+λ
3
+λ
4
=0；
3. 当满足(1)中条件时，方程组有唯一解还是无穷多解?
解：由于r(A)=r(B)=3＜4，所以该线性方程组有无穷多解．
4. 设函数z=e
xe
y
，求
解：
5. 设z是由方程x-mz=φ(y-nz)所确定的关于x，y的函数，证明：z满足方程
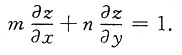
证：先求
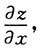
将方程x-mz=φ(y-nz)两边对x求偏导数，并注意到z是关于x，y的函数，得
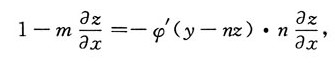
解得
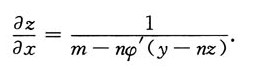
再将方程x-mz=φ(y-nz)两边对y求偏导数，得
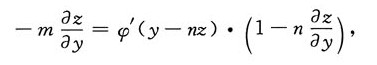
解得
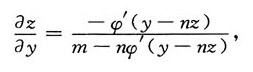
所以
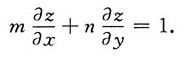
四、应用题
(本题10分．将解答的主要过程、步骤和答案填写在相应位置上)
1. 某厂每天生产Q件某种产品的成本函数为C(Q)=0.5Q
2
+36Q+9800(元)．为使平均成本最低，每天产量应为多少?此时，每件产品平均成本为多少?
因为
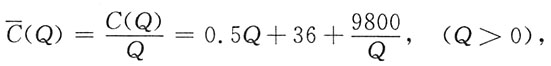
所以
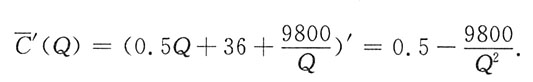
令
，得Q
1
=140，Q
2
=-140(舍去)．
Q
1
=140是函数
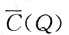
在其定义域内的唯一驻点，且该问题确实存在最小值．
所以Q
1
=140是平均成本函数
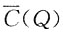
的最小值点，即为使平均成本最低，每天产量应为140件．
此时的平均成本为
一、单项选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
三、计算题
1
2
3
4
5
四、应用题
1
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
，则以下结论正确的是______
，根据保号性可知在点x=a的去心邻域内有f(x)-f(a)＞0，即f(x)＞f(a)，所以f(a)为函数的极小值，故选D．
，则x=______
所以x=3．
=______
在x=2处连续，则a=______
，又f(2)=a，根据连续的定义得
，故选B．
则dz|(1，2)=______
故fx(1，2)=1；
收敛，则下列级数中收敛的是______
收敛，而其他选项均发散．故选A．
故选B．
则p=______.
的收敛域为______．
收敛区间为
时，该级数为交错级数
收敛；
时，该级数为调和级数
发散．
的秩为______．
，故r(A)≠3．
，故A有二阶行列式不为零的子阵，所以r(A)=2．
的值等于______．
则
将方程x-mz=φ(y-nz)两边对x求偏导数，并注意到z是关于x，y的函数，得
，得Q1=140，Q2=-140(舍去)．
在其定义域内的唯一驻点，且该问题确实存在最小值．
的最小值点，即为使平均成本最低，每天产量应为140件．
深色：已答题 浅色：未答题