一、单项选择题(在每小题给出的四个备选项中,选出一个正确的答案)4. 微分方程dy-2xy
2dx=0满足条件y(1)=-1的特解是______
A.
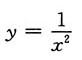
B.
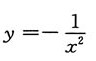
C.y=x
2 D.y=-x
2 A B C D
B
[解析] 对微分方程分离变量,得
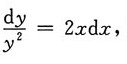
两边积分,得
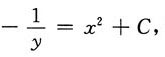
代入y(1)=-1,得C=0,故方程的特解为
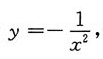
故选B.
6. 已知函数f(x)可导,且
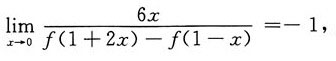
则曲线y=f(x)在点(1,f(1))处的切线斜率为______
A.
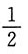
B.
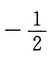
C.2
D.-2
A B C D
D
[解析]
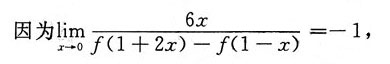

即f'(1)=-2.故选D.
7. 已知函数z=ln(x
2+y
2),则全微分dz|
(1,1)=______
A.
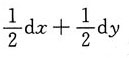
B.dy-dy
C.
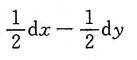
D.dx+dy
A B C D
D
[解析]
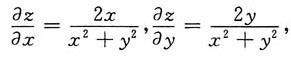
则
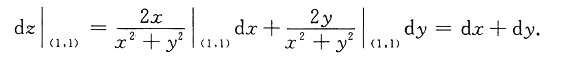
8. 函数
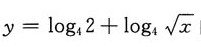
的反函数是______
- A.y=2x-1
- B.y=22x-1
- C.y=42x-1
- D.y=4x-1
A B C D
C
[解析]
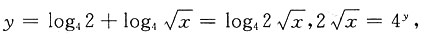
两边平方,得4x=4
2y,所以x=4
2y-1,
互换x与y得反函数为y=4
2x-1(-∞<x<+∞),故选C.
二、填空题1. 如果使函数
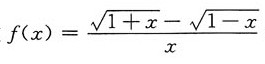
在点x=0处连续,应将其在点x=0处的函数值补充定义为______.
f(0)=1
[解析]
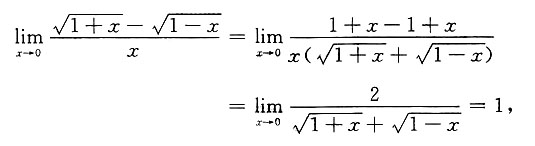
若f(x)在x=0处连续需补充定义f(0)=1.
2. 不定积分∫cos(3x+2)dx=______.
[解析]
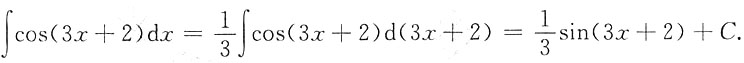
3. 已知函数
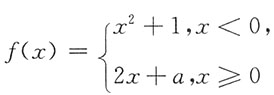
在x=0处连续,则a=______.
1
[解析] f(x)在x=0处连续,则
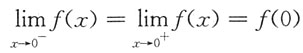
,又
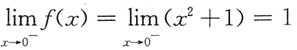
,
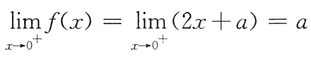
,所以a=1.
4. 函数f(x)=x
2-6x+4lnx的极小值是______.
4ln2-8
[解析]

由f'(x)=0得x=1或x=2.
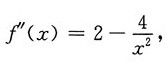
故f"(1)=-2<0,f"(2)=1>0,
利用极值第二充分条件,在x=2处取得极小值4ln2-8.
5. 若由参数方程
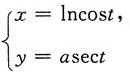
所确定的函数y=y(x)是微分方程
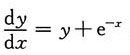
的解,则常数a=______.
[解析] 由题意有
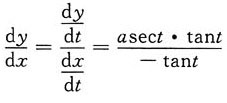
=-asect,y+e
-x=asect+e
-lncost=asect+sect=(a+1)sect,∴由

得-asect=(a+1)sect,(2a+1)sect=0,2a+1=0,
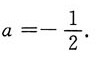
三、计算题(每小题10分,共40分.将解答的主要过程、步骤和答案填写在相应位置上)1. 求向量组α
1=(1,2,1,3),α
2=(4,-1,-5,-6),α
3=(-1,-3,-4,-7),α
4=(2,1,2,3)的一个极大线性无关组,并把其余向量用极大无关组线性表出.
解:

所以α
1,α
2,α
3是向量组的一个极大线性无关组.由α
4=k
1α
1+k
2α
2+k
3α
3得方程组
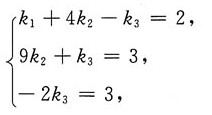
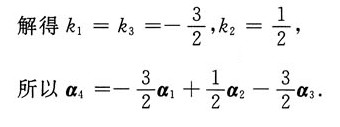
2. 解线性方程组
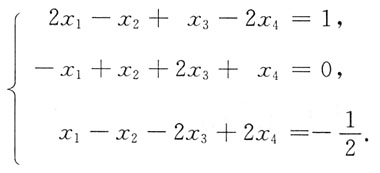
解:该线性方程组所对应的增广矩阵为
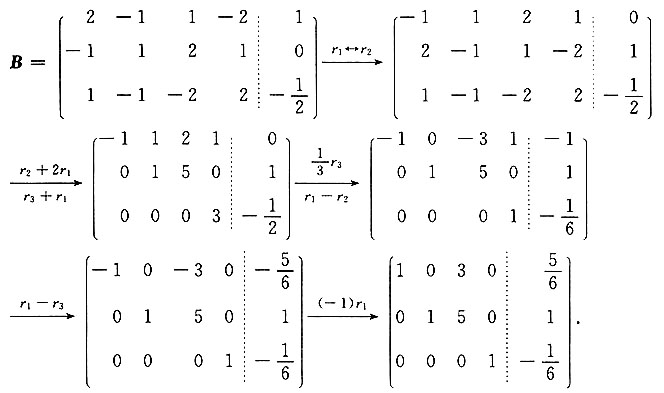
与原方程组同解的最简方程组为

将x
3作为自由未知量,则可化为

自由未知数x
3取任意实数k,则该线性方程组的通解为
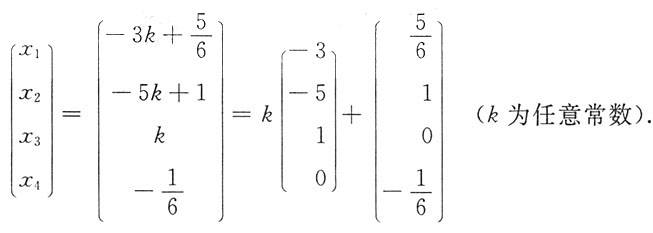
3. 计算不定积分
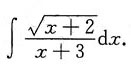
解:设
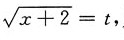
则x=t
2-2,dx=2tdt,
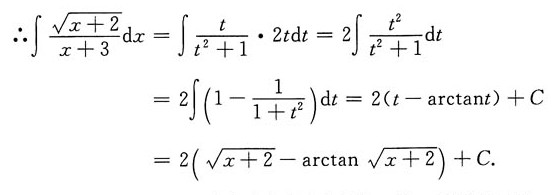
4. 已知线性方程组
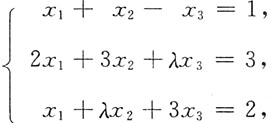
当λ为何值时,方程组有唯一解?无解?有无穷多解?当方程组有无穷多解时,求出线性方程组的通解.
解:设该线性方程组所对应的系数矩阵为A,方程组的增广矩阵为
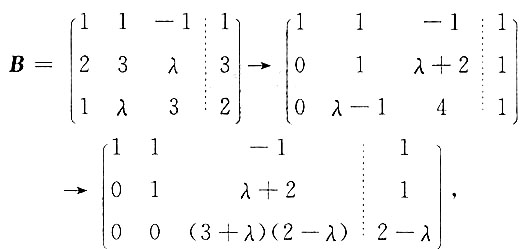
当λ≠-3且λ≠2时,方程组有唯一解;
当λ=-3时,r(A)=2,r(B)=3,方程组无解;
当λ=2时,方程组有无穷多解,
当λ=2时,有
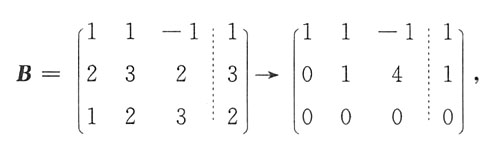
原方程组化为
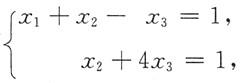
其特解为

,
齐次方程组为
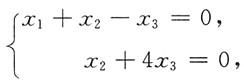
基础解系为
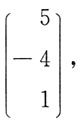
因此,原方程组的通解为
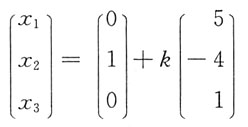
(k为任意常数).
四、应用题(本题10分.将解答的主要过程、步骤和答案填写在相应位置上)1. 一工厂每批生产某商品x台的费用为C(x)=5x+200(万元),得到的收益为R(x)=10x-0.01x
2(万元),问每批生产多少台,才能使利润最大?
解:利润函数为
π(x)=R(x)-C(x)=10x-0.01x2-5x-200
=5x-0.01x2-200,
π'(x)=5-0.02x,
令π'(x)=0得x=250,π"(250)=-0.02<0,故当x=250时,π(x)取得极大值,又由驻点唯一,而最值存在,则π(x)在x=250处取得最大值.即每批生产250台时,才能使利润最大.