银符考试题库B12
现在是：
试卷总分：150.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
福建省专升本考试高等数学分类模拟24
一、单项选择题
1. 直线
与平面x+2y-z+3=0的位置关系是______
A.互相垂直
B.互相平行但直线不在平面内
C.直线在平面内
D.斜交
A
B
C
D
C
[解析] s={3，-1，1}，n={1，2，-1}，
因为s·n=3×1+(-1)×2+1×(-1)=0，
所以直线与平面平行或直线在平面内.
又点(1，-1，2)代入平面方程x+2y-z+3=0成立.
所以直线在平面内.故应选C.
2. 点x=0是函数
的______
A.连续点
B.可去间断点
C.跳跃间断点
D.第二类间断点
A
B
C
D
C
[解析] 因为
所以x=0为跳跃间断点.故应选C.
3. 曲线y=kx
2
+1在点(1，2)处的切线斜率为2，则k=______
A.1
B.2
C.3
D.4
A
B
C
D
A
[解析] 由导数的几何意义可知，切线斜率为y'|
(1，2)
=2kx|
(1，2)
=2k=2，所以k=1．
4. 由参数方程
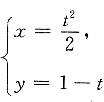
确定函数y(x)的二阶导数
______
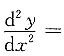
A．
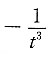
B．
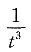
C．
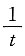
D．
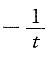
A
B
C
D
B
[解析] 因为
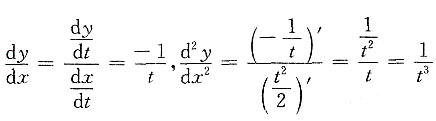
，故应选B.
5. 曲线
______
A.仅有水平渐近线
B.既有水平又有垂直渐近线
C.仅有垂直渐近线
D.既无水平又无垂直渐近线
A
B
C
D
B
[解析] 因为
所以y=0为水平渐近线，x=0为垂直渐近线，故应选B.
6. 设
______
A.e
x
siny
B.e
x
+e
x
siny
C.-e
x
cosy
D.-e
x
siny
A
B
C
D
D
[解析]
，故应选D.
7. 设
在x=0出连续，则a=______
A.-1
B.1
C.2
D.3
A
B
C
D
D
[解析] 因为
，所以由f(x)在x=0处连续，可知f(0)=3从而a=3，故选D.
8. 设f(x)为奇函数，则F(x)=f(x)(e
x
-e
-x
)为______
A.奇函数
B.偶函数
C.非奇非偶函数
D.无法确定
A
B
C
D
B
[解析] 因为F(-x)=f(-x)(e
-x
-e
x
)=f(x)(e
x
-e
-x
)=F(x).所以F(x)为偶函数，故应选B.
9. 方程y"-2y'+y=(x+1)e
x
的特解形式可设为______
A.x
2
(ax+b)e
x
B.x(ax+b)e
x
C.(ax+b)e
x
D.ae
x
A
B
C
D
A
[解析] 因为特征方程r
2
-2r+1=0有二重特征根r
1
=r
2
=1，又自由项f(x)=(x+1)e
x
中λ=1为特征重根，故方程的特解应设为y
*
=x
2
(ax+b)e
x
.
10. 已知|a|=1，|b|=5，且a·b=3，则|a×b|=______
A．4
B．
C．5
D．10
A
B
C
D
A
[解析] 因为
所以
从而
，应选A.
二、填空题
1. 函数
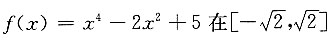
上最大值为______.
5
[解析] f'(x)=4x
3
-4x，令f'(x)=0得x=0，-1，1，
计算f(0)=5，f(±1)=4，
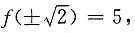
从而在
上的最大值为5.
2. 曲线y=xe
-x
的拐点是______.
(2，2e
-2
)
[解析] 因为y'=(1-x)e
-x
，y"=(x-2)e
-x
，令y"=0得x=2，
当x＜2时，y"＜0，当x＞2时，y"＞2，
故拐点坐标为(2，2e
-2
).
3.
0
[解析] 由于定积分
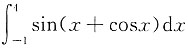
是个常数，故其导数为0．
4. 若
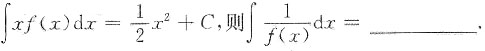
x+C
[解析] 两边求导得xf(x)=x，则f(x)=1，故
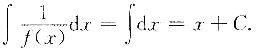
5. 若
______.
0
[解析] 因为z(x，0)=0，所以z
x
(x，0)=0，故
6.
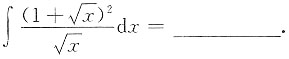
[解析]
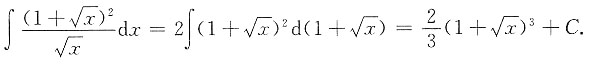
7. 函数
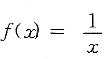
展开为x-1的幂级数为______.
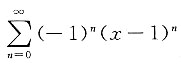
，x∈(0，2)
[解析]
8. 已知一阶导数
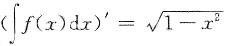
，则一阶导函数值f'(0)=______．
0
[解析]
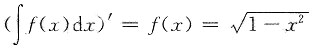
，则
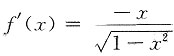
，所以f'(0)=0．
9. 点M(3，2，-1)到平面x+y+z-1=0的距离为______.
[解析]
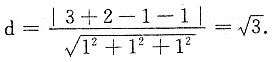
10.
0
[解析] 由于定积分
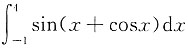
是个常数，故其导数为0．
三、计算题
1. 求
设
2. 已知函数
连续，求a．
∵f(x)连续，∴
，
又
∴2a=4，即a=2．
3. 讨论
在x=0处的连续性与可导性.
因为
则
所以f(x)在x=0处是连续的.
又
所以f(x)在x=0处不可导.
4. 求极限
四、应用题
1. 过点(1，0)作抛物线
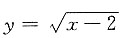
的切线，求这条切线、抛物线及x轴所围的平面图形绕x轴旋转一周得到的旋转体的体积.
设切点为(x
0
，y
0
)，
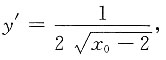
由于
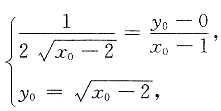
解得切点为(3，1)，
所以切线方程为
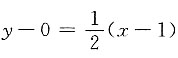
，即
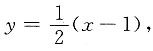
所以求旋转体的体积为
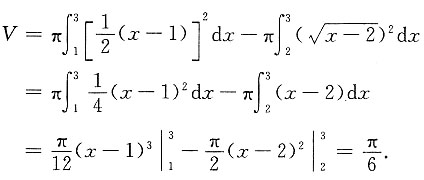
五、证明题
1. 设f(x)在区间[0，1]上连续，且f(x)＜1，证明：方程
在区间(0，1)内仅有一个实根.
证：设
因为f(x)在[0，1]上连续，所以F(x)也在[0，1]上连续.
F(0)=-1＜0，
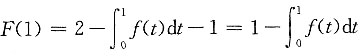
，由于f(t)＜1，则
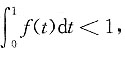
故F(1)＞0，由零点定理可知至少存在一个ξ∈(0，1)使F(ξ)=0.
又因为F'(x)=2-f(x)＞0，F(x)在(0，1)上单调增加，
因此方程
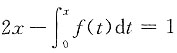
在(0，1)内仅有一个实根.
一、单项选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
6
7
8
9
10
三、计算题
1
2
3
4
四、应用题
1
五、证明题
1
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
与平面x+2y-z+3=0的位置关系是______
的______
确定函数y(x)的二阶导数
______
，故应选B.
______
______
，故应选D.
在x=0出连续，则a=______
，所以由f(x)在x=0处连续，可知f(0)=3从而a=3，故选D.
，应选A.
上最大值为______.
上的最大值为5.
是个常数，故其导数为0．
______.
展开为x-1的幂级数为______.
，x∈(0，2)
，则一阶导函数值f'(0)=______．
，则
，所以f'(0)=0．
连续，求a．
，
在x=0处的连续性与可导性.
则
的切线，求这条切线、抛物线及x轴所围的平面图形绕x轴旋转一周得到的旋转体的体积.
解得切点为(3，1)，
，即
在区间(0，1)内仅有一个实根.
，由于f(t)＜1，则
在(0，1)内仅有一个实根.
深色：已答题 浅色：未答题