一、选择题在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列极限正确的是
A.
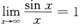
B.
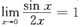
C.
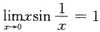
D.
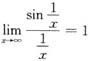
A B C D
D
[解析] A项:
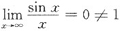
,无穷小
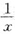
与有界变量sinx的乘积仍是无穷小.
B项:
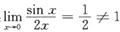
.
C项:
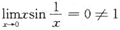
,无穷小x与有界变量
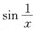
乘积仍是无穷小.
D项:
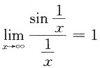
,根据重要极限Ⅰ可得.
5. 函数f(x)=|2x-1|在点

处的导数是
A.0 B.
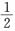
C.2 D.不存在
A B C D
D
[解析] 绝对值求导的关键是去绝对符号,然后根据分段函数求导数.
因为
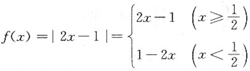
所以
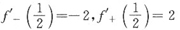
因为
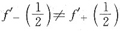
,所以在
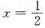
处的导数不存在.
9. 同时抛掷两颗正六面体的骰子,则出现点数和等于6的概率为
A.
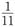
B.
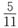
C.
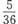
D.
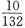
A B C D
C
[解析] 设事件A表示两骰子点数之和等于6,因为同时抛掷两颗骰子所含基本事件共有:6×6=36种,事件A所含基本事件共有5种,所以
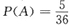
.
三、解答题解答应写出推理、演算步骤.
1. 若
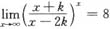
,求k的值.

由题设知e
3k=8,故k=ln2.
[解析] 由于是“
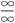
”型,先消去高阶无穷因子,再利用重要极限Ⅱ对分子分母分别进行变形,并求极限.
2. 若f(x)存在二阶导数,求函数y=f(lnx)的二阶导数.
[解析] 这是抽象函数的求导问题,而f(lnx)又是复合函数,所以应用复合函数的求导公式来计算.
3. 计算
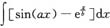
.
[解析] 虽有字母a,b,但只有x才是积分变量,将a,b看作常数,采用凑微分法即可.
4. 求函数
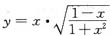
的导数.
等式两边同时取对数得
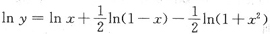
方程两边同时对z求导有

故
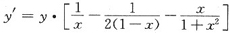
(将y代入)
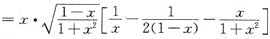
[解析] 对多个函数的连乘除求导数,用对数求导法将大大简化计算.在所给函数式两边分别取对数,再用隐函数求导方法求y'.注意在y'表达式中不可保留y,而应用x的函数式代替.
5. 计算
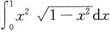
.
设x=sint,则dx=costdt,当x=0时,t=0;x=1时,
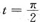
,所以
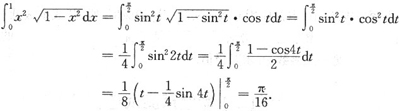
[解析] 因为式中有形如
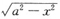
的无理式,则应设x=asint;若有
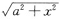
时,则应设x=atant;同理有
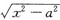
时,应设x=asect.这是在解答此类题时必须掌握的.
6. 设
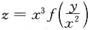
,其中f为可微函数.证明
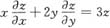
.
[解析] 这是抽象的求偏导数的问题,只需注意:对x求偏导时,y当作常数,对y求偏导时,x当作常数,再用一元函数的求导公式即可.
7. 求函数z=x
2+y
2-xy在条件x+2y=7下的极值.
设F(x,y,λ)=x
2+y
2-xy+λ(x+2y-7),
则

由①与②解得5x=4y,代入③得x=2,
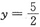
,
所以
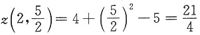
为极值.
[解析] 本题主要考查二元函数的条件极值.通常先构造拉格朗日函数,再求解
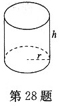
8. 某工厂要制造一个无盖的圆柱形发酵池,其容积是

,池底的材料30元/m
2,池壁的材料20元/m
2,问如何设计,才能使成本最低,最低成本是多少元?
设池底半径为r,池高为h(如图所示),则

,得
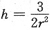
.
又设制造成本为S,则
S=30·πr
2+20·27πrh
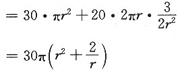
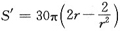
令S'=0,得驻点r=1.
因为
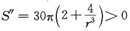
所以r=1为唯一的极小值,即为最小值点.
所以,池底半径为1m,高为
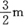
时,可使成本最低,最低成本为90π元.
[解析] 本题考查的知识点是应用导数求实际问题的极值.所谓“成本最低”,即求制造成本函数在已知条件下的最小值.因此,本题的关键是正确写出制造成本函数的表达式,再利用已知条件将其化为一元函数,并求其极值.