银符考试题库B12
现在是:
试卷总分:120.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
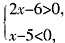 ,解得,3<x<5。
,解得,3<x<5。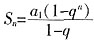 ,若|q|<1,则
,若|q|<1,则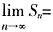 ______。
______。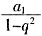
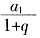
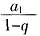
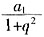
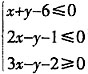 ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为______。
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为______。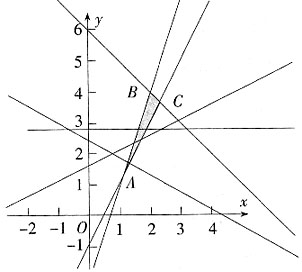

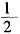 ×4π×12=2π,故S=S1+S2=π+24。
×4π×12=2π,故S=S1+S2=π+24。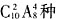
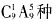
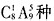
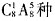
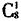 种结果。接着从9种不同的作物种子中选出5种放入5个不同的瓶子中展出,实际上是从9个元素中选5个排列,共有
种结果。接着从9种不同的作物种子中选出5种放入5个不同的瓶子中展出,实际上是从9个元素中选5个排列,共有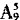 种结果。根据分步计数原理知共有
种结果。根据分步计数原理知共有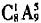 种结果。
种结果。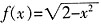 ,则
,则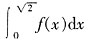 的值为______。
的值为______。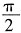
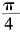
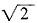 的上半圆,定积分表示的四分之一圆面积。
的上半圆,定积分表示的四分之一圆面积。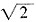
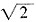 。
。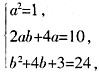 解得:a=-1,b=-7,或a=1,b=3,则5a-b=2。
解得:a=-1,b=-7,或a=1,b=3,则5a-b=2。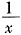 )8的展开式中常数项为______。(用数字作答)
)8的展开式中常数项为______。(用数字作答)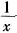 )8的展开式中常数项为
)8的展开式中常数项为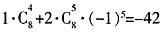 。
。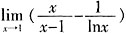 =______。
=______。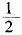
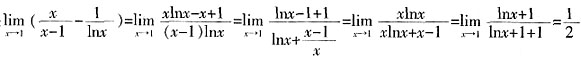 。
。| 高校 | 相关人数 | 抽取人数 | |||||||||||||||||
| A | 18 | x | |||||||||||||||||
| B | 36 | 2 | |||||||||||||||||
| C | 54 | y | |||||||||||||||||
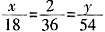 ,解可得x=1,y=3;
,解可得x=1,y=3;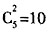 种,
种,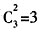 种;
种;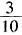 。
。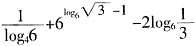 的值;
的值;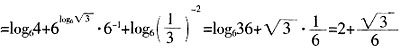 。
。 的值。
的值。 ,
,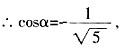
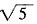 。
。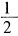 x2+bx+c,
x2+bx+c,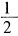 x平行的切线,求b的取值范围;
x平行的切线,求b的取值范围;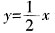 平行的切线,则
平行的切线,则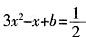 有解,则有
有解,则有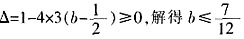 。
。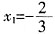 ,x2=1。
,x2=1。
| x | 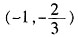
|
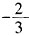
|
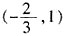
|
1 | (1,2) | |||||||||||||||||||||||||||||||||||
| f'(x) | + | 0 | - | 0 | + | |||||||||||||||||||||||||||||||||||
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 | |||||||||||||||||||||||||||||||||||
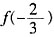 和f(2)二者中取到,
和f(2)二者中取到,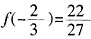 +c,f(2)=2+c,则f(x)在x∈[-1,2]上的最大值为2+c。因为函数f(x)=x3-
+c,f(2)=2+c,则f(x)在x∈[-1,2]上的最大值为2+c。因为函数f(x)=x3-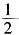 x2+bx+c<c2恒成立,即有2+c<c2,解得c<-1或c>2。
x2+bx+c<c2恒成立,即有2+c<c2,解得c<-1或c>2。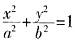 (a>b>0)离心率是
(a>b>0)离心率是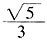 ,若左焦点到直线
,若左焦点到直线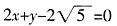 距离为4。
距离为4。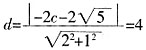 ,解得
,解得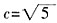 ,因为
,因为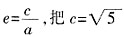 代入,得a=3,由b2+c2=a2,得b=2。所以椭圆方程为
代入,得a=3,由b2+c2=a2,得b=2。所以椭圆方程为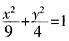 。
。 ,求λ的取值范围。
,求λ的取值范围。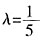 。
。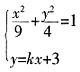 得(4+9k2)x2+54kx+45=0,Δ=1296k2-720,
得(4+9k2)x2+54kx+45=0,Δ=1296k2-720,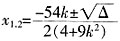 ,由假设k>0得,
,由假设k>0得,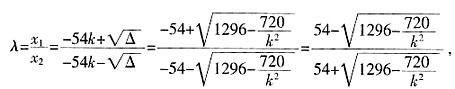
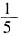 。综上所述λ的范围是[
。综上所述λ的范围是[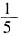 ,1)。
,1)。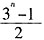 ……②式
……②式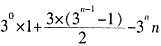 ,
,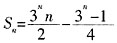 。
。 。
。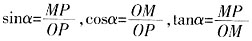 。(如图)
。(如图)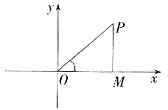
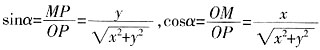 ,你能否使表达式变得简单些?
,你能否使表达式变得简单些?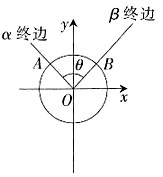
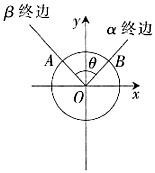
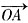 =(cosα,sinα),
=(cosα,sinα),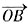 =(cosβ,sinβ)。
=(cosβ,sinβ)。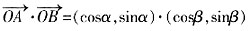
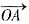 与
与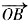 夹角为θ,则
夹角为θ,则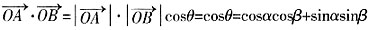 。
。