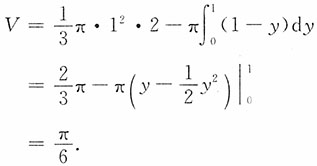三、计算题每小题8分,共80分.计算题要有计算过程.1. 设函数
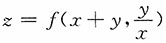
,其中f(x)具有二阶连续偏导数,求
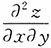
.
解:令u=x+y,
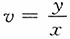
,由复合函数求偏导法则可得
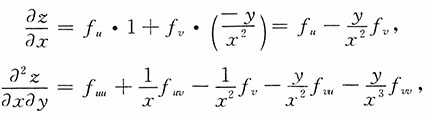
由于f(x,y)具有二阶连续偏导数,则f
uv=f
vu,
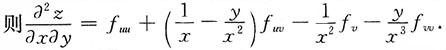
2. 求函数u=xsin2y+z在点P(1,0,1)处沿从点P(1,0,1)到点Q(2,-1,1)的方向的方向导数.
解:这里方向l即为
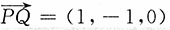
,
l的方向余弦为
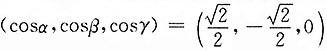
,
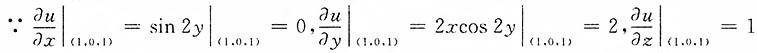
,
故所求方向导数为
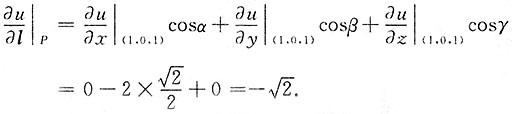
3. 求函数
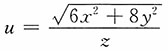
在点P(1,1,1)处的沿方向n=(4,6,2)的方向导数.
4. 求解二阶微分方程y"+3y'+2y=20cos2x的通解.
解:特征方程为r2+3r+2=0,特征根为r1=-1,r2=-2,
所以对应的齐次方程的通解为
Y=C1e-x+C2e-2x.
由于±2i不是特征根,故可设方程的特解为
y*=Acos2x+Bsin2x,
因为(y*)'=-2Asin2x+2Bcos2x,(y*)"=-4Acos2x-4Bsin2x,把y*、(y*)'、(y*)"代入原方程整理得
(-2A+6B)cos2x-(6A+2B)sin2x=20cos2x,
所以A=-1,B=3,于是所求方程的特解为
y*=-cos2x+3sin2x,
所以,方程的通解为
y=C1e-x+C2e-2x-cos2x+3sin2x.
5. 求函数
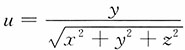
在点M(1,2,-2)处沿曲线
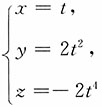
在点M处的切线方向的方向导数.
解:曲线在M(1,2,-2)点处对应t=1,故切线的方向向量为l=(1,4t,-8t
3)|
t=1=(1,4,-8),其单位向量
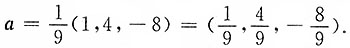
由
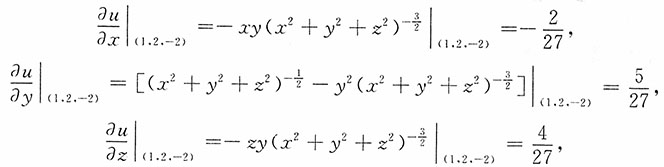
于是
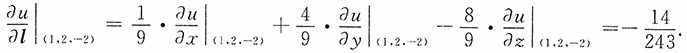
6. 计算
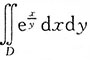
,其中D是由y=1,y=x,y=2,x=0所围成的闭区域.
解:积分区域如图所示,
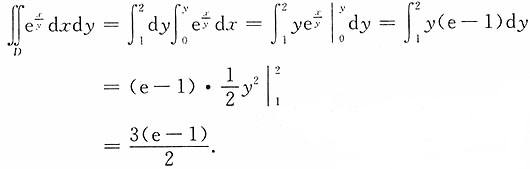
7. 计算二重积分
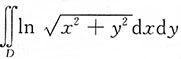
,其中D={(x,y)|1≤x
2+y
2≤4}.
解:该二重积分适合选择极坐标系下进行计算,且D可表示为0≤θ≤2π,1≤r≤2.故
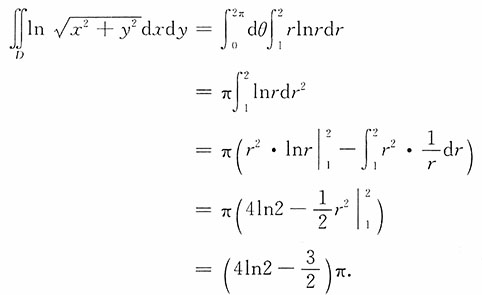
8. 求函数u=e
x2+y2+z2在点P(-1,0,1)处沿着点P到点Q(2,0,-2)的方向的方向导数.
解:由题可知
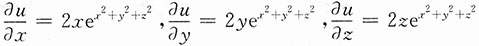
,
则
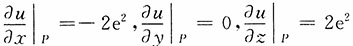
,
令
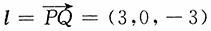
,
则方向余弦
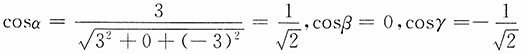
,
故方向导数为
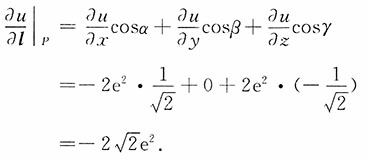
9. 求不定积分
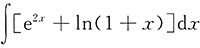
.
解:

10. 设
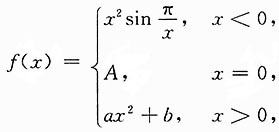
求常数A,a,b的值,使f(x)在x=0处可导,并求f'(0).
解:由可导必连续知
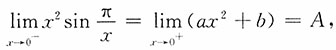
所以,A=b=0.
又
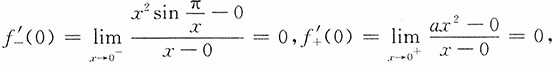
所以,a可以为任意常数,且f'(0)=0.
四、应用题与证明题每小题10分,共20分.应用题的计算要有计算过程,证明题要有证明过程.平面图形D由曲线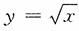 ,直线y=x-2及x轴所围成.
,直线y=x-2及x轴所围成.1. 求此平面图形的面积;
解:以y为积分变量,则所求面积为

2. 求此平面图形绕x轴旋转一周而成的旋转体体积.
解:该图形绕x轴旋转所成体积为
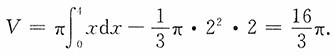
3. 求抛物线y=1-x
2及其在点(1,0)处的切线和y轴所围成图形的面积,并计算该图形绕y轴旋转一周所成旋转体的体积.
解:平面图形如图所示,因y'=-2x,所以k=-2,
从而经过点(1,0)的切线方程为y=-2x+2.
所求平面图形的面积为
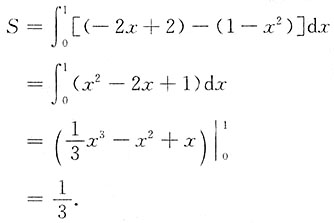
该图形绕y轴旋转一周所成旋转体的体积为