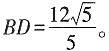一、单项选择题2. 根据下列算法语句,当输入x为60时,输出y的值为______
输入x
If x≤50 Then
y=0.5*x
Else
y=25+0.6*(x-50)
End If
输出y
A B C D
C
[解析] 由程序框图可知,该程序的作用是计算并输出分段函数y=
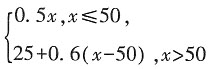
的函数值。当x=60时,y=25+0.6(60-50)=31,故选C。
二、填空题1. 设函数
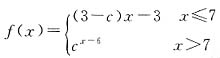
,数列{a
n}满足a
n=f(n),n∈N*,且数列{a
n}是递增数列,则实数c的取值范围是______.
(2,3)
[解析] 数列{a
n}是递增数列,所以有
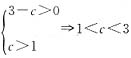
,f(7)<f(8).所以7(3-c)-3<c
2,解得c<-9,或c>2,所以,实数c的取值范围是(2,3).
2. 已知向量a=(1,3),b=(-2,-4),且(2a-mb)∥(a+b),则m=______。
-2
[解析] 由已知可得,2a-mb=(2+2m,6+4m),a+b=(-1,-1),又因为(2a-mb)∥(a+b),故
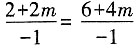
,解得m=-2。
3. 二项式
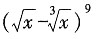
的展开式中有理项的项数为______。
2
[解析] 根据题意,二项式的展开式的通项为
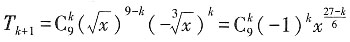
,所以当k=3和k=9时展开项为有理项。
4. 极限
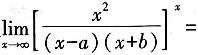
______。
ea-b
[解析]
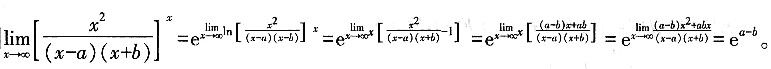
5. 如果一桶油连桶重8千克,用去2/7后连桶重6千克,那么原来桶中有油______千克,桶重______千克.
7 1
[解析] 由题意:m
桶+m
油=8,
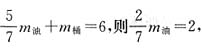
m
油=7,m
桶=1.
三、解答题如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC。
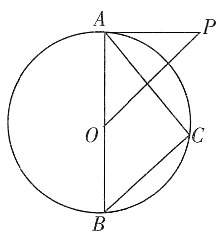
1. 求证:PA为⊙O的切线;
证:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°。
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°。
∵∠P=∠BAC,
∴∠P+∠AOP=90°。
∴∠PAO=90°,即OA⊥AP。
又∵OA是⊙O的半径,
∴PA为⊙O的切线。
2. 若OB=5,
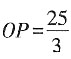
,求AC的长。
解:由(1)知,∠PAO=90°。
∵OB=5,
∴OA=OB=5。
又
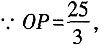
∴在Rt△APO中,
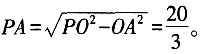
由第一小题知,∠ACB=∠PAO=90°。
∵∠BAC=∠P,
∴△ABC∽△POA,
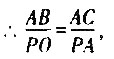
∴
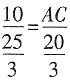
,解得AC=8,即AC的长度为8。
3. 已知甲、乙两煤矿每年产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地。东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格为1元/吨和1.5元/吨。乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨。煤矿应怎样编制调运方案,能使总运费最少?
解:设甲煤矿向东车站运了x万吨,乙煤矿向东车站运了y万吨,总运费为W。
由题可得方程组:
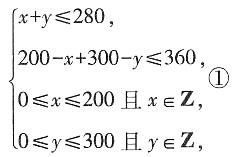
且有总运费W=[1×x+1.5(200-x)+0.8y+1.6(300-y)]×10
4=10
4×(780-0.5x-0.8y),②
②可进一步化作y=-0.625x+975-1.25x10
-4W。③
可画出①的图象,如图所示:
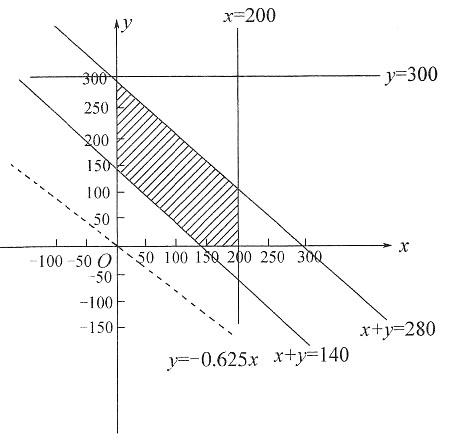
利用线性规划可知,当
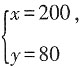
时总运费最小,
此时总运费W=10
4×(780-0.5×200-0.8×80)=616×10
4。
答:甲煤矿应全部通过东车站运输,乙煤矿应通过东车站运输80万吨,通过西车站运输220万吨,此时有最小运费为616万元。
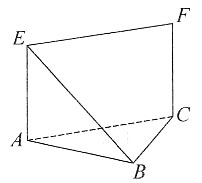
4. 求证:AB⊥平面BCF;
证:∵∠ABC=90°,
∴AB⊥BC。
又∵EA⊥平面ABC,FC∥EA,
∴AB⊥FC。
∵BC∩FC=C,
∴AB⊥平面BCF。
5. 证明五点A,B,C,E,F在同一个球面上,并求A,F两点的球面距离。
证:由第一小题知,△ABF为直角三角形,且∠ABF=90°。
记EC与AF交于点O。
∵四边形ACFE是矩形,
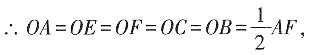
∴A,B,C,E,F在以O为球心,AF为直径的球面上,
∴A,F两点之间的球面距离就是半个大圆的弧长,为
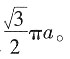
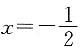 对称,且f'(1)=0.
对称,且f'(1)=0.6. 求实数a、b的值;
解:f'(x)=6x
2+2ax+b,
∵若函数y=f'(x)的图象关于直线
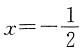
对称,且f'(1)=0,
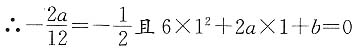
,解得a=3,b=-12.
7. 求函数f(x)的极值.
解:代入a=3,b=-2得f(x)=2x
3+3x
2-12x+1,
f'(x)=6x
2+6x-12=6(x+2)(x-1),
f(x)的变化如下:
| x |
(-∞,-2) |
-2 |
(-2,1) |
1 |
(1,+∞) |
| f'(x) |
+ |
0 |
- |
0 |
+ |
| f(x) |
↗ |
极大值21 |
↘ |
极小值-6 |
↗ |
当x=1时,f(x)取极小值,极小值为-6;当x=-2时,f(x)取极大值,极大值为21.
8. 已知定义在R上的奇函数f(x),满足f(x-4)=f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x
1、x
2、x
3、x
4,求四数之和x
1+x
2+x
3+x
4。
解:因为定义在R上的奇函数,满足f(x-4)=-f(x),所以f(x-4)=f(-x)。由f(x)为奇函数,所以函数图象关于直线x=2对称且f(0)=0。
由f(x-4)=-f(x)知f(x-8)=f(x),所以函数是以8为周期的周期函数。又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数。
如图所示,那么方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x
1,x
2,x
3,x
4,不妨设x
1<x
2<x
3<x
4,由对称性知x
1+x
2=-12、x
3+x
4=4。所以x
1+x
2+x
3+x
4=-12+4=-8。
9. 客车与货车同时从A,B两地相向而行,第一次相遇时距离A地140千米,然后各自按原来速度继续行驶,分别到达对方出发地后立即沿原路返回。第二次相遇时离A地的距离是A,B两地距离的60%,A,B两地距离为多少千米?
解:(算式解法)两车第一次相遇时一共行了1个AB的路程,从开始到第二次相遇,两车一共行了3个AB的路程,可以推算出客车、货车各自共所行的路程分别是第一次相遇前各自所走的路程的3倍,即客车共走的路程是140×3=420千米,客车一共走了全程的(1+40%),据此解答即可。
140×3÷(1+40%)=300(千米)
(方程解法)设AB距离为S千米,则第二次相遇时客车行驶了1.4S千米,火车行驶了1.6S千米,设客车速度v
1千米/时,货车速度为v
2千米/时,第一次相遇时,客车行驶140千米,则火车行驶(S-140)千米,则列出方程如下:

化简得140:(S-140)=7:8,解得S=300
答:A、B两地的距离为300千米。
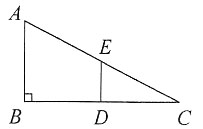
图1
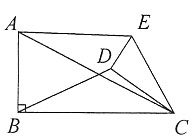
图2

备用图
10. 问题发现
①当α=0°时,
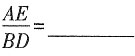
;②当α=180°时,
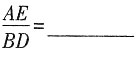
。
解:
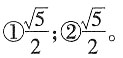
11. 拓展探究
试判断:当0°≤α<360°时,
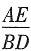
的大小有无变化?请仅就图2的情形给出证明。
解:无变化。
在图1中,∵DE是△ABC的中位线,
∴DE∥AB,
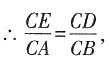
∠EDC=∠B=90°。
如图2,∵△EDC在旋转过程中形状大小不变,
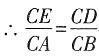
然成立。
又∵∠ACE=∠BCD=α,
∴△ACE∽△BCD,
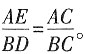
在Rt△ABC中,
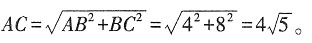

12. 问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长。
解:

[提示] 当△EDC在BC上方,且A,D,E三点共线时,四边形ABCD为矩形,∴
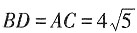
;当△EDC在BC下方,且A,D,E三点共线时,△ADC为直角三角形,由勾股定理可求得AD=8,∴AE=6,根据
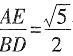
可求得
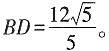
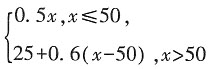 的函数值。当x=60时,y=25+0.6(60-50)=31,故选C。
的函数值。当x=60时,y=25+0.6(60-50)=31,故选C。
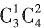 种不同的选法;②A类选修课选2门,B类选修课选1门,有
种不同的选法;②A类选修课选2门,B类选修课选1门,有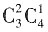 种不同的选法,所以不同的选法共有
种不同的选法,所以不同的选法共有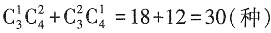 。
。 。
。
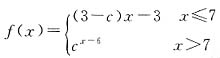 ,数列{an}满足an=f(n),n∈N*,且数列{an}是递增数列,则实数c的取值范围是______.
,数列{an}满足an=f(n),n∈N*,且数列{an}是递增数列,则实数c的取值范围是______.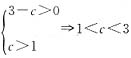 ,f(7)<f(8).所以7(3-c)-3<c2,解得c<-9,或c>2,所以,实数c的取值范围是(2,3).
,f(7)<f(8).所以7(3-c)-3<c2,解得c<-9,或c>2,所以,实数c的取值范围是(2,3).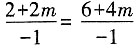 ,解得m=-2。
,解得m=-2。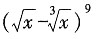 的展开式中有理项的项数为______。
的展开式中有理项的项数为______。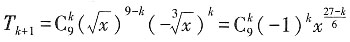 ,所以当k=3和k=9时展开项为有理项。
,所以当k=3和k=9时展开项为有理项。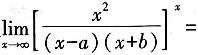 ______。
______。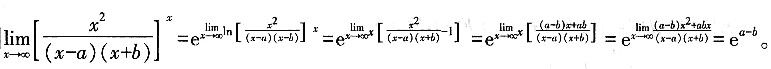
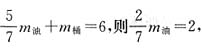 m油=7,m桶=1.
m油=7,m桶=1.
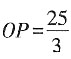 ,求AC的长。
,求AC的长。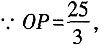
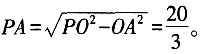
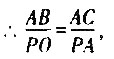
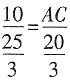 ,解得AC=8,即AC的长度为8。
,解得AC=8,即AC的长度为8。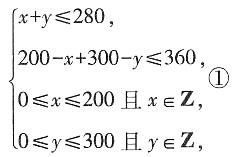

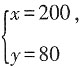 时总运费最小,
时总运费最小,
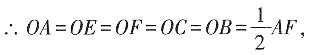
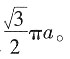
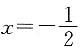 对称,且f'(1)=0.
对称,且f'(1)=0.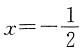 对称,且f'(1)=0,
对称,且f'(1)=0,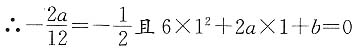 ,解得a=3,b=-12.
,解得a=3,b=-12.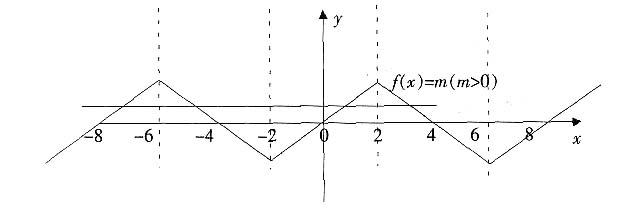




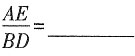 ;②当α=180°时,
;②当α=180°时,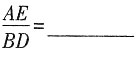 。
。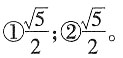
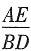 的大小有无变化?请仅就图2的情形给出证明。
的大小有无变化?请仅就图2的情形给出证明。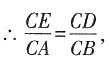 ∠EDC=∠B=90°。
∠EDC=∠B=90°。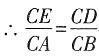 然成立。
然成立。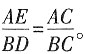
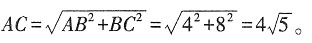


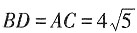 ;当△EDC在BC下方,且A,D,E三点共线时,△ADC为直角三角形,由勾股定理可求得AD=8,∴AE=6,根据
;当△EDC在BC下方,且A,D,E三点共线时,△ADC为直角三角形,由勾股定理可求得AD=8,∴AE=6,根据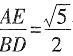 可求得
可求得