一、单项选择题2. 如图,在棱长为2的正方体ABCD—A
1B
1C
1D
1中,E为BC的中点,点P在线段D
1E上,点P到直线CC
1的距离的最小值为______.
A.1
B.
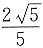
C.
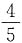
D.
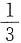
A B C D
B
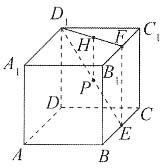
[解析] 如图所示,过E点作EF//CC
1,交B
1C
1于F,连接D
1F.再过P点作PH//EF交D
1F于H.所以PH//CC
1,点P到直线CC
1的距离即为点H到CC
1的距离,又因为CC
1⊥面A
1B
1C
1D
1,H∈面A
1B
1C
1D
1,连接C
1H,C
1H即为H到CC
1的距离,也就是P到CC
1的距离.当C
1H为Rt△D
1C
1F斜边上的高时,距离最短.根据面积相等原理,
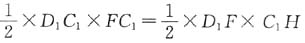
,解得
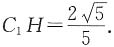
7. 如图,在三棱锥S—ABC中,E为棱SC的中点,若AC=
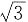
,SA=SB=SC=AB=BC=1,则异面直线AC与BE所成的角为______.
A B C D
C
[解析] 如图所示,取SA的中点F,连接EF、BF.EF是△SAC的中位线,则
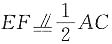
,则∠BEF是异面直线AC与BE所成的角,EF=
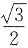
,又因为SA=SB=AB=1,F为SA的中点.所以BF=
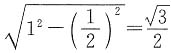
,同理,BE=
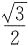
,故BE=BF=EF,△BEF是等边三角形,所以∠BEF=60°.
9. 圆x
2+y
2-2x-1=0关于直线2x-y+3=0对称的圆的方程是______
A.
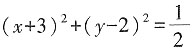
B.
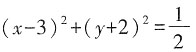
C.(x+3)
2+(y-2)
2=2
D.(x-3)
2+(y+2)
2=2
A B C D
C
[解析] 因为两圆关于直线对称,所以两圆的半径相等,圆心关于直线对称。因为x
2+y
2-2x-1=0化成标准方程为(x-1)
2+y
2=2,所以所求圆的半径为

。下面只要求出圆心(1,0)关于直线2x-y+3=0的对称点的坐标即可。不妨将其设为(x
0,y
0),可知点(1,0)和点(x
0,y
0)的中点在直线2x-y+3=0上,所以有
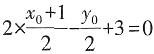
。又两点的连线与直线2x-y+3=0垂直,则
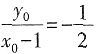
,解得x
0=-3,y
0=2。
二、填空题1. 数学是人类的一种文化,它的内容、______、______和语言是现代文明的重要组成部分。
2. 发现法又称为研究法、现代启发式或问题教学法,美国心理学家______是这种教学方法的积极倡导者。
3. 若直线l:ax+2y+6=0与直线l
2:x+(a-1)y+(a
2-1)=0平行且不重合,则a的值是______。
-1
[解析] 若直线l:ax+2y+6=0与直线l2:x+(a-1)y+(a2-1)=0平行,则a(a-1)-2=0,即a2-a-2=0,解得a=2或a=-1。又a=2时,l1:x+y+3=0与l2:x+y+3=0重合,故a=-1。
4. 如图,面积为12cm
2的△ABC沿BC方向平移至△DEF位置,平移的距离是BC的三倍,则图中四边形ACED的面积为______cm
2。
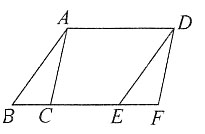
60
[解析] ∵△DEF是△ABC平移得到的,∴AD∥CF,AD=CF,∴四边形ACFD是平行四边形。
∵S
△ABC=12,CF=3BC,△ABC和
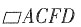
的高相等,
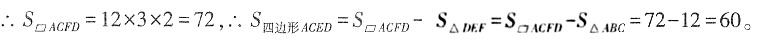
5. 已知a,b是不共线的向量,
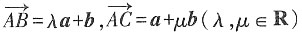
,则A,B,C三点共线的充要条件是______。
λμ=1
[解析] 由
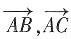
有公共点A,则若A,B,C三点共线,故
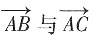
共线,因此存在一个实数t,使
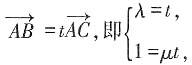
消去参数t得λμ=1。反之,当λμ=1时,
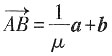
,此时存在实数
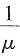
使
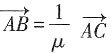
,故

共线。又由
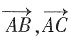
有公共点A,则A,B,C三点共线,故A,B,C三点共线的充要条件是λμ=1。
三、解答题假设某市2011年新建住房面积400万平方米,其中有250万平方米是中低价房。预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%。另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米。那么,到哪一年年底,1. 该市历年所建中低价房的累计面积(以2011年为累计的第一年)将首次不少于4750万平方米?
解:设中低价房面积形成数列{a
n}。
由题意可知{a
n}是等差数列,其中a
1=250,d=50,
则
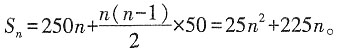
令25n
2+225n≥4750,即n
2+9n-190≥0。
因为n是正整数,
所以n≥10。
所以到2020年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米。
2. 当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
解:设新建住房面积形成数列{bn}。
由题意可知{bn}是等比数列,其中b1=400,q=1.08,则bn=400·(1.08)n-1。
由题意可知an>0.85bn,则250+(n-1)·50>400·(1.08)n-1·0.85。
解得满足上述不等式的最小正整数n=6,
则到2016年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%。
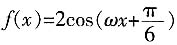 (其中ω>0,x∈R)的最小正周期为10π。
(其中ω>0,x∈R)的最小正周期为10π。3. 求ω的值;
解:
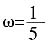
5. 水果商要把荔枝售价至少定为多少才不会亏本?
解:设购进荔枝k千克,荔枝售价定为y元/千克时,水果商才不会亏本。
由题意得y·k(1-5%)≥(5+0.7)k。
∵k>0,
∴95%y≥5.7,
∴y≥6。
∴水果商要把荔枝售价至少定为6元/千克才不会亏本。
6. 在销售过程中,水果商发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系:m=-10x+120,那么当销售单价定为多少时,每天获得的利润W最大?
解:由上一小题可知,每千克荔枝的平均成本为6元。
由题意得W=(x-6)m=(x-6)(-10x+120)=-10(x-9)2+90。
∵a=-10<0,
∴当x=9时,W有最大值。
∴当销售单价定为9元/千克时,每天可获利润最大。
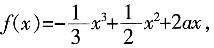
7. 若f(x)在
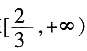
上存在单调递增区间,求a的取值范围;
解:由
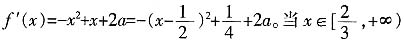
时,f'(x)的最大值为
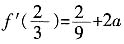
;令

,得
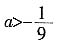
。所以,当
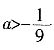
时,f(x)在
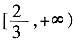
上存在单调递增区间。
8. 当0<a<2时,f(x)在[1,4]上的最小值为
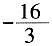
,求f(x)在该区间上的最大值。
解:令f'(x)=0,得两根
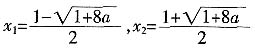
,所以f(x)在(-∞,x
1),(x
2+∞)上单调递减,在(x
1,x
2)上单调递增;当0<α<2时,有x
1<1<x
2<4,所以,f(x)在[1,4]上的最大值为,

,即f(4)<f(1)。所以,f(x)在[1,4]上的最小值为
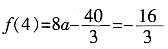
,得a=1,x
2=2,从而f(x)在[1,4]上的最大值为
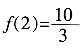
。
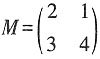 。
。10. 求矩阵M的特征值及特征向量。
解:矩阵M的特征多项式为
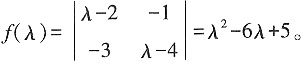
令f(λ)=0,得矩阵M的特征值为1或5。
当λ=1时,由二元一次方程
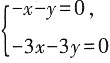
得x+y=0。
令x=1,则y=-1,故特征值λ=1对应的特征向量
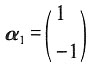
。
当λ=5时,由二元一次方程
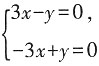
得3x-y=0。
令x=1,则y=3,故特征值λ=5对应的特征向量

。
11. 一个圆形水池,半径为6米,深2米,现在要在水池底面和侧面贴上瓷砖,求贴上瓷砖部分的面积是多少?如果在水池中装满水,能装多少立方米水?
解:(1)水池的侧面积为2×3.14×6×2=75.36(平方米),
水池的底面积为3.14×62=113.04(平方米),
贴瓷砖的面积为75.36+113.04=188.4(平方米)。
(2)水池的容积为3.14×62×2=3.14×36×2=226.08(立方米)。
答:贴上瓷砖部分的面积是188.4平方米,能装226.08立方米的水。
12. 所有能被6整除的数都能被3整除.
解:命题的否定:存在能被6整除的数,不能被3整除.
否命题:不能被6整除的数都不能被3整除.
13. 若a>2,b>2,则a+b>4.
解:命题的否定:若a>2,b>2,则a+b≤4.
否命题:若a≤2,b≤2,则a+b≤4.
14. 存在实数x,使x>3.
解:命题的否定:对任意实数x,都有x≤3.
否命题:不存在实数x,使x≤3.
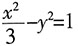 的左焦点重合,则a的值为______。
的左焦点重合,则a的值为______。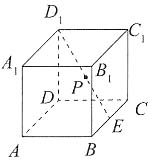
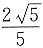
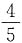
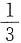
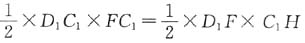 ,解得
,解得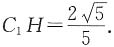
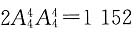
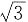 ,SA=SB=SC=AB=BC=1,则异面直线AC与BE所成的角为______.
,SA=SB=SC=AB=BC=1,则异面直线AC与BE所成的角为______.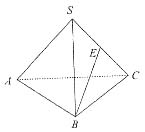
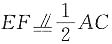 ,则∠BEF是异面直线AC与BE所成的角,EF=
,则∠BEF是异面直线AC与BE所成的角,EF=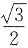 ,又因为SA=SB=AB=1,F为SA的中点.所以BF=
,又因为SA=SB=AB=1,F为SA的中点.所以BF=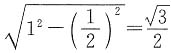 ,同理,BE=
,同理,BE=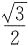 ,故BE=BF=EF,△BEF是等边三角形,所以∠BEF=60°.
,故BE=BF=EF,△BEF是等边三角形,所以∠BEF=60°.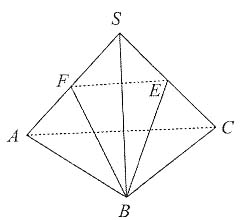


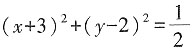
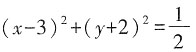
 。下面只要求出圆心(1,0)关于直线2x-y+3=0的对称点的坐标即可。不妨将其设为(x0,y0),可知点(1,0)和点(x0,y0)的中点在直线2x-y+3=0上,所以有
。下面只要求出圆心(1,0)关于直线2x-y+3=0的对称点的坐标即可。不妨将其设为(x0,y0),可知点(1,0)和点(x0,y0)的中点在直线2x-y+3=0上,所以有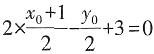 。又两点的连线与直线2x-y+3=0垂直,则
。又两点的连线与直线2x-y+3=0垂直,则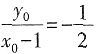 ,解得x0=-3,y0=2。
,解得x0=-3,y0=2。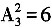 (种)。从0,2中选一个数字2,则2排在十位时,从1,3,5中选两个数字排在个位与百位,共有
(种)。从0,2中选一个数字2,则2排在十位时,从1,3,5中选两个数字排在个位与百位,共有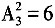 (种);2排在百位时,从1,3,5中选两个数字排在个位与十位,共有
(种);2排在百位时,从1,3,5中选两个数字排在个位与十位,共有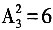 (种)。故共有
(种)。故共有 (种)。
(种)。
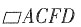 的高相等,
的高相等,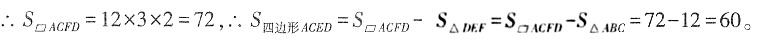
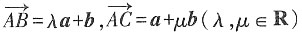 ,则A,B,C三点共线的充要条件是______。
,则A,B,C三点共线的充要条件是______。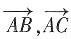 有公共点A,则若A,B,C三点共线,故
有公共点A,则若A,B,C三点共线,故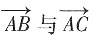 共线,因此存在一个实数t,使
共线,因此存在一个实数t,使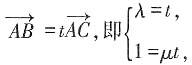 消去参数t得λμ=1。反之,当λμ=1时,
消去参数t得λμ=1。反之,当λμ=1时,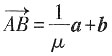 ,此时存在实数
,此时存在实数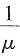 使
使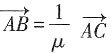 ,故
,故 共线。又由
共线。又由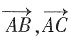 有公共点A,则A,B,C三点共线,故A,B,C三点共线的充要条件是λμ=1。
有公共点A,则A,B,C三点共线,故A,B,C三点共线的充要条件是λμ=1。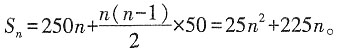
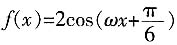 (其中ω>0,x∈R)的最小正周期为10π。
(其中ω>0,x∈R)的最小正周期为10π。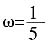
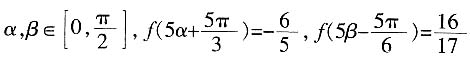 ,求cos(α+β)的值。
,求cos(α+β)的值。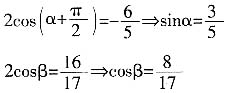
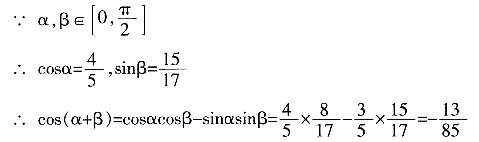
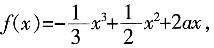
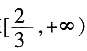 上存在单调递增区间,求a的取值范围;
上存在单调递增区间,求a的取值范围;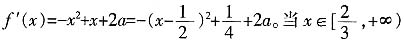 时,f'(x)的最大值为
时,f'(x)的最大值为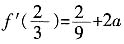 ;令
;令 ,得
,得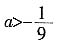 。所以,当
。所以,当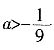 时,f(x)在
时,f(x)在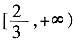 上存在单调递增区间。
上存在单调递增区间。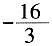 ,求f(x)在该区间上的最大值。
,求f(x)在该区间上的最大值。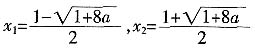 ,所以f(x)在(-∞,x1),(x2+∞)上单调递减,在(x1,x2)上单调递增;当0<α<2时,有x1<1<x2<4,所以,f(x)在[1,4]上的最大值为,
,所以f(x)在(-∞,x1),(x2+∞)上单调递减,在(x1,x2)上单调递增;当0<α<2时,有x1<1<x2<4,所以,f(x)在[1,4]上的最大值为, ,即f(4)<f(1)。所以,f(x)在[1,4]上的最小值为
,即f(4)<f(1)。所以,f(x)在[1,4]上的最小值为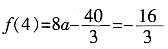 ,得a=1,x2=2,从而f(x)在[1,4]上的最大值为
,得a=1,x2=2,从而f(x)在[1,4]上的最大值为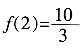 。
。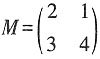 。
。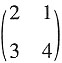 的行列式为
的行列式为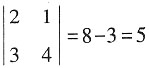 ,
,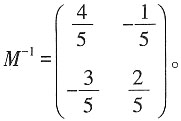
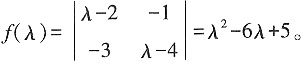
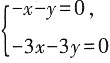 得x+y=0。
得x+y=0。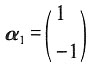 。
。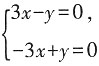 得3x-y=0。
得3x-y=0。 。
。