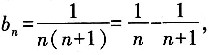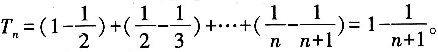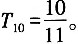银符考试题库B12
现在是:
试卷总分:120.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
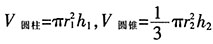 ,由题意V圆柱:V圆锥=5:6,即
,由题意V圆柱:V圆锥=5:6,即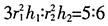 ,故
,故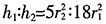 ,又r1:r2=2:3,所以h1:h2=5:8,故选A。
,又r1:r2=2:3,所以h1:h2=5:8,故选A。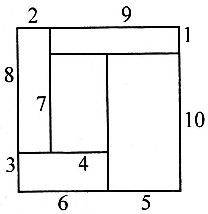

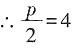 ,∴p=8,故抛物线方程为y2=16x。
,∴p=8,故抛物线方程为y2=16x。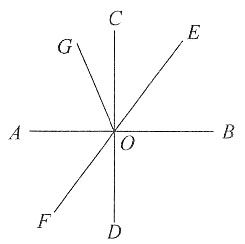
 ,则
,则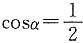 ”的逆否命题是______.
”的逆否命题是______.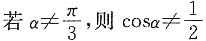
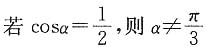
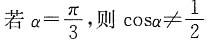
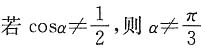
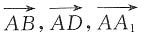 两两的夹角均为60°,且
两两的夹角均为60°,且 ,
,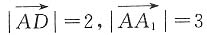 ,则
,则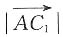 等于______.
等于______.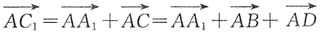 ,则
,则 ,又因为
,又因为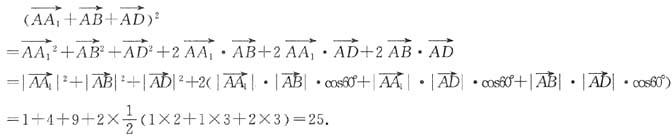
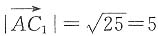 .
.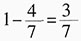 与短蜡烛的
与短蜡烛的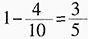 相等,则短蜡烛与长蜡烛的长度之比为5:7。
相等,则短蜡烛与长蜡烛的长度之比为5:7。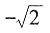
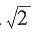
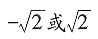
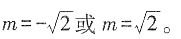
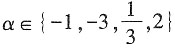 ,则使函数y=xα的定义域为R且在(-∞,0)上单调递增的α值为______。
,则使函数y=xα的定义域为R且在(-∞,0)上单调递增的α值为______。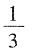
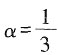 时,函数y=xα的定义域为R且在(-∞,0)上单调递增,故
时,函数y=xα的定义域为R且在(-∞,0)上单调递增,故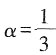 成立。
成立。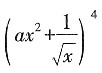 展开式中x3的系数为
展开式中x3的系数为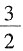 ,则
,则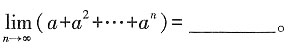
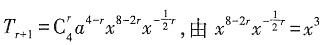 ,得r=2,由
,得r=2,由 ,所以
,所以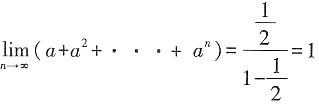 ,所以所求极限为1。
,所以所求极限为1。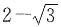
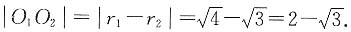
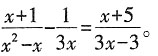

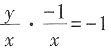 。
。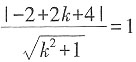 ,即3k2+8k+3=0,①
,即3k2+8k+3=0,①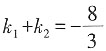 ,k1k2=1。
,k1k2=1。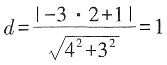 ,
,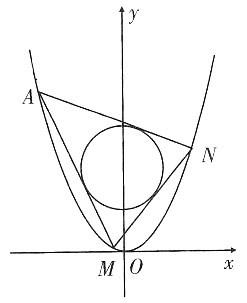
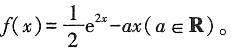
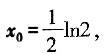
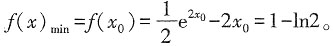
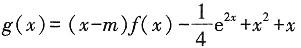 在区间(0,+∞)上为增函数,求整数m的最大值。
在区间(0,+∞)上为增函数,求整数m的最大值。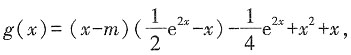
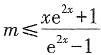 恒成立。
恒成立。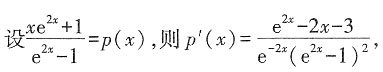
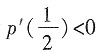 ,p'(1)>0,
,p'(1)>0,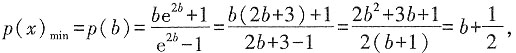
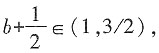
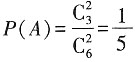 。
。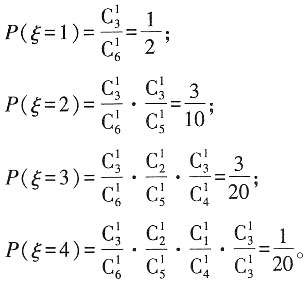
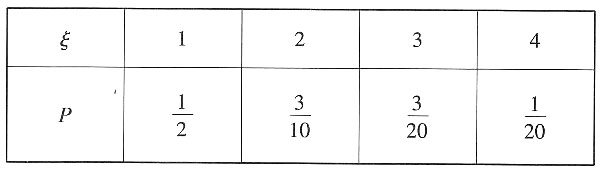
 。
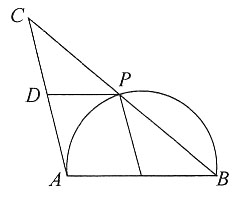
。
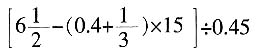
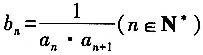 ,求数列{bn}前10项的和。
,求数列{bn}前10项的和。